Ce rapport de stage traite de l'utilisation de l'ozone mesuré par satellite pour valider les modèles climatiques dans le cadre du projet IASI-Metop. Le document aborde divers aspects tels que la normalisation des modèles climatiques, la mesure et l'interprétation des données d'ozone, ainsi que la confrontation entre les données satellitaires et les modèles. L'objectif final est d'évaluer l'impact des changements climatiques et de la pollution sur l'ozone atmosphérique.





![Chapitre 1
Contexte
1.1 Le CNES
Le Centre National d’Etudes Spatiales (CNES), créé en 1961 est un établissement public à
caractère industriel et commercial (EPIC). Il fait suite au Comité de recherches spatiales mis
en place par le président De Gaulle en 1959 afin de faire face au manque de coordination des
études spatiales de la France. Dorénavant, participant également aux programmes conduits par
l’Agence Spatiale Européenne (ESA), le CNES est un acteur incontournable sur la table euro-
péenne des activités et programmes spatiaux.
Le CNES vise plusieurs objectifs. Le premier est de promouvoir de nouvelles applications
spatiales civiles, militaires ou scientifiques via la recherche et l’innovation, garantissant un ac-
cès autonome de la France à l’espace, mais aussi d’accroître les connaissances de notre planète,
protégeant ses ressources et prévenant les risques naturels dans un objectif de développement
durable, à l’aide d’application au grand public entre autres.
Pour cela, il est décomposé en 4 centres, regroupant plus de 2418 agents (en 2007 [1]
dont 37% de femmes, 76% d’ingénieurs et de cadres). Le siège social (Paris) met en œuvre
la politique spatiale de la France au sein de l’Europe, définissant les grandes stratégies et les
programmes prioritaires. La Direction des lanceurs (Evry, Essonne) se charge du développe-
ment des lanceurs Ariane, accompagnant la phase de production industrielle pour le compte
d’Arianespace. Le centre spatial guyanais (Kourou) est le "port spatial" de l’Europe, là d’où
sont envoyés les lanceurs Ariane ainsi que ceux de l’ESA. Enfin, le Centre Spatial de Toulouse
(CST), qui s’étend sur 56.5 ha, dispose d’un large éventail de compétences, créant les systèmes
spatiaux depuis la conception des satellites et instruments, jusqu’à leur exploitation en orbite.
1.2 Le projet IASI-MetOp
1.2.1 Le satellite MetOp
Développé dans le cadre du projet EPS (Eumetsat Polar System) d’Eumetsat (EUropean or-
ganisation for the exploitation of METeorological SATellites), installant une collaboration entre
l’Europe et les Etats-Unis pour une période allant de 2005 à 2020, le satellite MetOp a été mis
en orbite en 2006 sur un lanceur de type SOYOUZ depuis Baïkonour au Kazakhstan dans le
but d’améliorer les prévisions météorologiques, ainsi que la climatologie et la chimie de l’at-
mosphère ([2]). Il est le premier d’une série de trois MetOp, le prochain étant programmé pour
avril 2012. Ainsi, de nombreux instruments ont été placés à bord : HIRS, sondant optiquement
la température et l’humidité atmosphérique ; AVHRR pour l’imagerie optique des nuages, du
6](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-6-320.jpg)

![1.2.2 IASI, Interféromètre Atmosphérique de Sondage Infrarouge
Elément clef du satellite MetOp, IASI (Infrared Atmosphere Sounding Interferometer) est
un instrument issu d’une coopération entre le CNES et Eumetsat ([2]). Il a été conçu au sein
du CNES et vise à mesurer deux fois par jour le spectre du rayonnement infrarouge émis par la
terre, à partir de l’orbite héliosynchrone de faible altitude du satellite MetOp.
Ainsi, l’instrument IASI utilise un procédé d’interférométrie optique permettant la décom-
position spectrale fine du rayonnement infrarouge de l’atmosphère, puis ensuite traite numéri-
quement les données obtenues à l’aide d’un sous-système embarqué réalisant une transformée
de Fourier inverse et un étalonnage radiométrique. Cela retranscrit alors les spectres de vibra-
tion et de rotation des molécules atmosphériques (voir section 3.2.1). Pour se faire, l’instrument
est composé d’un miroir de balayage pour une acquisition de 2000 km de large perpendicu-
lairement à la trace du satellite, d’un télescope afocal, d’un interféromètre de Michelson (de
différence de marche optique de 2 cm), et d’un miroir de repliement.
Afin de couvrir environ 99% de la surface de la Terre deux fois par jour, le miroir de balayage
permet d’atteindre à 48,3 ˚ de part et d’autre de la trace du satellite, l’observation se fait de
type "pas à pas" avec un système de stabilisation du champ visuel. 30 sondages sont réalisés
à intervalle régulier le long de chaque ligne de balayage correspondant à 2x15 positions de
miroir. Chaque champ visuel instantané (3,3˚× 3,3˚ou 50 km × 50 km au nadir) est composé
de 2 × 2 pixels circulaires, correspondant à une empreinte de 12 km de diamètre au nadir (voir
figure C.1).
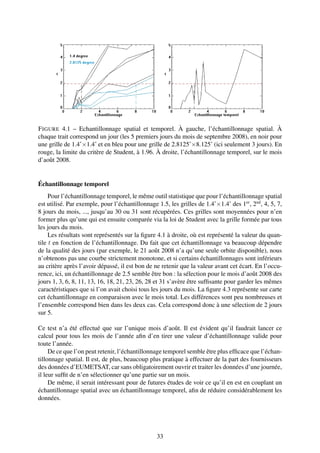
F IGURE 1.2 – à gauche, les pincipaux éléments composant l’interféromètre IASI. A droite, le
mode d’osbervation de IASI : l’instrument mesure le spectre infrarouges émis par la Terre et
l’atmosphère sur une largeur d’environ 2200 km, tous les 50 km au nadir avec 4 empreintes de
12 km de diamètre (crédits images : ESA, CNES)
L’instrument IASI englobe une large gamme spectrale (8461 canaux spectraux), allant de
la limite de l’infrarouge thermique à 3,62 µm (2760 cm-1 ) jusqu’à 15,5 µm (645cm-1 ) couvrant
ainsi le pic de l’infrarouge termique et la bande du CO2 ([3]). Cette région spectrale permet plu-
sieurs applications via IASI comme le profil de température (à l’aide des bandes d’absorptions
du CO2 ), les propriétés nuageuses, le profil d’humidité (à l’aide de l’H2 O). Pour optimiser les
performances de l’instruments, le domaine spectral a été subdivisé en trois bandes ([645 ; 1210]
cm-1 , [1210 ; 2000] cm-1 et [2000 ; 2760] cm-1 ) avec une résolution spectrale avant échantillon-
nage variant entre et 0,25 et 0,5 cm-1 .
8](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-8-320.jpg)
![1.3 Changement climatique et ozone
Afin de comprendre au mieux l’utilisation des données du satellite IASI, il faut avoir un
regard critique sur ce que l’on appelle "changement climatique".
La plupart du temps, un abus de language fera entendre le terme de "réchauffement cli-
matique". Mais malgré le fait qu’il a été certifié scientifiquement (entre autres par le Groupe
d’experts Intergouvernemental sur l’évolution du climat GIEC [4]) que la température globale
de la Terre croît d’année en année, c’est bien de changements climatiques dont il est question.
D’une part, les activités anthropologiques du 20ème siècle sont à l’origine d’une multiplication
par six de la teneur en chlorure stratosphérique (Cl- , [5]) et d’un doublement du bromure (Br- ),
ce qui a réduit de façon considérable la couche d’ozone sur la globalité du monde, créant le
trou dans la couche d’ozone au dessus de l’Antarctique. Une fois les effets démasqués, le Proto-
cole de Montréal a engendré d’importants changements sur certaines émissions atmosphériques.
Grâce à ces interventions, le niveau des halogènes stratosphériques a vu son sommet autour des
années 2000 et devrait redescendre progressivement durant le 21ème siècle.
D’autre part, les activités humaines ont créé une hausse significative des gaz à effet de serre
(GES) provoquant de façon certaine ([6]) le changement climatique alors identifié. Au niveau
de la stratosphère, ce dernier est lié de façon intrinsèque à la quantité d’ozone, via de nombreux
processus impliquant la température, les transports de composés chimiques, le rayonnement
Ultra-Violet (UV), les radicaux d’hydrogène et d’azote ([7]).
De même que les concentrations en GES ont contribué aux modifications de température,
de convection des masses d’air, ledit changement climatique affecte lui aussi la possibilité
qu’a l’ozone de retourner à un niveau "normal" dans la stratosphère, estimé par les spécialistes
comme étant le niveau pré-années 1980 (voire 1960). Cette restitution (retour à un niveau nor-
mal) de l’O3 dépend fortement des substances détruisant l’ozone (ODS pour Ozone depleting
substances). Ces substances comme le Brome ou le Chlore sont censées (d’après le Protocole de
Montreal) décroître de façon importante ([5]). Mais, malgré cela, les simulations GEOS-CCM
indiquent que selon les régions du monde, selon les périodes, la restitution de l’O3 sera diffé-
rent. Par exemple, il faudra certainement attendre plusieurs décennies avant que certaines zones
retrouvent la quantité d’ozone d’avant 1980 alors que d’autres zones comme les tropiques et les
latitudes moyennes au sud au niveau de la stratosphère basse risquent de ne jamais retrouver le
niveau d’antan ([7] & [5]).
9](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-9-320.jpg)
![Chapitre 2
Normalisation des modèles de climat
2.1 Les différents modèles de climat
2.1.1 Généralités
En 2003, le projet phare "Stratospheric Processes And their Role in Climate" (SPARC) du
World Climate Research Programme (WCRP) a initié le Chermistry-Climate Model Validation
(CCMVal) afin d’améliorer les connaissances sur les Modèles de Chimie et Climat (Chemistry-
Climate Model, CCM) et leurs modèles sous-jacents de circulation générale. Ainsi, de nom-
breuses simulations ont été réalisées pour en ressortir des évaluations, des discussions et des
analyses de données ([8]).
Tous les modèles de climat suivants sont utilisés pour le Chemistry-Climate Model Vali-
dation 2 (CCMVal-2) ([9]) et certains ont aussi été utilisés pour le CCMVal-1 avant de subir
des développements. Il y en a 16 en tout, provenant de diverses organisations avec pour but de
modéliser au mieux les réactions atmosphériques afin de projeter à l’avenir le climat global.
Pour chacune des méthodes, il existe différentes évolutions de l’ozone constatées, plus ou
moins précises et concordantes les unes avec les autres, mais qui donnent une idée assez globale
de l’évolution de l’ozone à long terme, résumée dans la dernière section, moyennant les sorties
obtenues ([9]).
2.1.2 Outils
Les modèles climatiques sont tous basés sur une même structure (voir figure 2.1) divisée
en trois parties : la chimie, la dynamique et les radiations. Ces trois parties résument à elles
seules l’atmosphère via un noyau dynamique, de la physique diabatique, un schéma de transport,
des modules de chimie et microphysiques associés aux changements de composition chimique.
Ainsi de nombreux modèles de climat cités par la suite se basent sur cette description. Il faut
alors expliciter un peu plus en détail les divers composants.
10](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-10-320.jpg)


![Transport
Il existe deux types de transports atmosphériques principaux : l’advection et les transports
convectifs. Ceux-ci sont complétés par les mélanges turbulents des espèces chimiques.
Tout d’abord, l’advection prend place en particulier dans la stratosphère basse où les temps
de vie des espèces chimiques sont plus longs que le temps de vie dynamique (des transports en
somme). L’advection correspond au transport horizontal de propriétés physico-chimiques du fait
du transport par les vents ou les courants de particules concernées. Les modèles peuvent se baser
sur différents traceurs météorologiques comme le moment, la chaleur, l’humidité, mais aussi
chimiques. L’advection est elle-même divisée en plusieurs méthodes : l’advection de volume
fini, spectrale, semi-Lagrangienne, etc.
Ensuite, la convection et les turbulences mélangent rapidement l’air et les espèces chimiques
verticalement. Ces processus sont cruciaux dans la troposphère et dans le milieu de l’atmo-
sphère car ils jouent un rôle prédominant dans les échanges intercontinentals et les transports
hémisphériques. En particulier, l’ozone troposphérique devient très important car il sera direc-
tement entraîné vers les couches hautes de la troposphère. Cependant, du fait que beaucoup de
CCMs ne prennent pas en compte la chimie troposphérique, des modèles sophistiqués ne sont
pas requis pour les transports convectifs et les turbulences.
2.1.3 Liste
Evolution moyenne de l’Ozone constatée. Avant le CCMVal-2, il a été établi dès 2006
que la restitution entière de l’ozone se ferait dès lors que les substances qui appauvrissent la
couche d’ozone (SAO ou ODS en anglais) n’affectent plus significativement l’ozone. Ainsi,
la restitution était prévue pour 2065 au-dessus de l’Antarctique et quelques décennies plus tôt
pour les autres latitudes. Pour le premier point, les modèles du CCMVal-2 ont mis en relation
la restitution de l’ozone avec la disparition par exemple de la chlorure, avec en évidence, des
différences sur les résultats. Selon les modèles, l’ozone revient plus vite que le chlorure disparaît
et vice-versa. Suites aux simulations de CCMVal-2, on peut constater que les changements de
l’ozone sont approximativement dépendant de Cly + αBry (Cly pour chlorure et Bry pour
Bromure) avec des valeurs différentes. Il est montré aussi que la restitution de l’ozone de 1960
prendrait 50% de temps supplémentaire par rapport au niveau d’ozone de 1980.
Les résultats mettent aussi en évidence une forte asymétrie suivant l’hémisphère, jusqu’à
l’Antarctique dont la restitution de l’ozone se fait plus lentement qu’en Arctique (la cause prin-
cipale est la circulation Brewer-Dobson, un courant faible de l’hémisphère hivernal qui redistri-
bue l’air). De même, dans les hautes latitudes du sud, les simulations ne sont pas assez longues
pour retrouver un niveau pré-année 1970.
Dans les tropiques, la colonne totale d’ozone est en accord avec les observations alors
qu’elle diffère légèrement dans les moyennes latitudes du fait que les modèles peuvent avoir
des biais de 10 à 20 DU.
AMTRAC3
Outils du modèle. AMTRAC3 est la version améliorée de AMTRAC ([10]). Ici, des nou-
veaux modèles de noyaux dynamiques en "sphères cubiques" ont été rajoutés, ainsi que des
nouveaux modèles de convection, des modifications des aérosols. Ainsi, la vapeur d’eau strato-
sphérique y est très précise mais le chlore et le brome ne sont pas modélisés. La paramétrisation
des CFCs de même que les taux de photolyse ont été corrigés. Enfin, la résolution verticale
stratosphérique a été augementée.
Evolution de l’Ozone constatée. AMTRAC3 constate l’une des plus faible réduction de
l’ozone dans la haute stratosphère. Côté observations, le modèle se trouve légèrement en deça
13](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-13-320.jpg)
![F IGURE 2.2 – Date de la restitution de l’ozone selon l’année de référence (abscisse) sur dif-
férentes couches de l’atmosphère décomposée en isobares ([9]). Les zones blanches corres-
pondent au fait que le modèle moyen ne constate pas de restitution de l’ozone à la fin de la
simulation, c’est-à-dire passé 2094.
14](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-14-320.jpg)
![au niveau des tropiques et latitudes moyennes, simule de manière très correcte le trou de la
couche d’ozone. La restitution est consistante avec le modèle moyen et AMTRAC3 se distingue
par une sensibilité accrue aux NOy dans les tropiques par rapport aux autres modèles.
CAM3.5
Outils du modèle. CAM3.5 est issu de l’ évolution du Community Atmosphere Model et
montre une bonne capacité à reproduire les changements à grande échelle dans la stratosphère
malgré un maximum d’altitude faible (∼40 km). ([11]). Ce modèle a récemment intégré de
nouvelles paramétrisations concernant les ondes gravitationnelles.
Evolution de l’Ozone constatée. CAM3.5 a un grand bias en ozone au niveau de la haute
stratosphère tropicale et l’une des plus faibles réductions. Le modèle est, comme AMTRAC3
légèrement en dessous des mesures au niveau des tropiques et latitudes moyennes. Le trou
d’ozone polaire est plus faible que les observations mais la restitution est consistante avec la
moyenne des CCMs.
CCSRNIES
Outils du modèle. CCSRNIES provient de l’agence météorologique japonaise basée sur un
modèle préexistant. Des améliorations du code ont été apportées comme le module de chimie
stratosphérique, incorporant une limite supérieure dans la mésosphère et un module de chimie
hétérogène (dont la chimie du bromure et d’autres éléments).
Evolution de l’Ozone constatée. Ce modèle montre l’un des plus forts refroidissement pour
la haute stratosphère, impliquant une restitution de l’ozone rapide. Il montre aussi un haut BIAS
dans les régions froides de l’Antarctique en fin d’hiver et printemps mais sous-estime en taille
et profondeur le trou dans la couche d’ozone.
CMAM
Outils du modèle. Basé sur le modèle de circulation générale GCM du Canadian Center for
Climate Modelling and Analysis (CCCma), CMAM ([12]) possède une résolution précise avec
une augmention monotone de 100 m à la surface jusqu’à 2,5 km dans la stratosphère/milieu
de l’atmosphère en passant par 900 m autour de la tropopause extra-tropicale. Le modèle est
couplé à un modèle de circulation océanique générale utilisant une résolution horizontale de
1,86˚avec 29 niveaux. CMAM inclut aussi une représentation compréhensive de la chimie stra-
tosphérique avec tous les cycles de perte de l’ozone catalytique. Une condition limite à ∼95
km est imposée pour les NOx pour comptabiliser la production de NOx mésosphériques par les
rayons cosmiques et les particules solaires.
Evolution de l’Ozone constatée. CMAM possède une colonne d’ozone inférieure aux ob-
servations dans les tropics et les latitudes moyennes du nord. Il montre aussi une baisse réduite
en ozone due à un faible niveau de Cly par rapport au modèle moyen, mais par contre, la restitu-
tion de l’ozone est similaire avec quelques décalages temporels en Arctique et dans les latitudes
moyennes du sud.
CNRM-ACM
Outils du modèle. Le GCM du Centre National de Recherches Météorologiques utilise son
propre schéma de transport ([13]) et distingue selon la résolution horizontale la dynamique de
la chimie afin de réduire le temps de calcul a contrario de la résolution verticale.
15](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-15-320.jpg)
![Evolution de l’Ozone constatée. CNRM-ACM montre une réduction de l’ozone plus im-
portante que les observations au niveau des tropiques et des latitudes moyennes ainsi qu’une
largeur plus importante du trou en Antarctique.
Il s’agit du modèle utilisé pour effectuer la confrontation avec les mesures satellitaires IASI
d’EUMETSAT dans les parties suivantes.
E39CA
Outils du modèle. Basé sur le Modèle du Centre Européen d’HAmbourg (ECHAM), les
traceurs chimiques et hydrologiques sont transportés avec le modèle purement Lagrangien AT-
TILA, conservant la masse et strictement non diffusif ([14]).
Evolution de l’Ozone constatée. E39CA montre un biais très important dans la haute stra-
tosphère tropicale et de surcroît, le biais est le plus important de tous les modèles sur les tro-
piques. Le modèle possède une petite aire pour le trou d’ozone, et indique une restitution d’en-
viron une décennie avant le modèle moyen.
EMAC
Outils du modèle. EMAC est un système de simulation de climat et chimie numérique qui
inclut des sous-modèles décrivant les processus troposphériques et de l’atmosphère moyenne
([15] et [16]). Il utilise la première version du Modular Earth Submodel System (MESSy1)
pour lier les codes informatiques de plusieurs instituts. Son noyau est basé sur l’ECHAM. Il
inclut aussi une représentation mésosphérique de de la production des NOx par le rayonnement
cosmique et les particules solaires.
Evolution de l’Ozone constatée. Ce modèle exhibe un petit et peu profond trou d’ozone,
en partie à cause de la région de faible température (inférieure à 195 K) qui est plus petite
qu’observée.
GEOS-CCM
Outils du modèle. Partant du Goddard Earth Observing System (GEOS) version 5 AGCM
(Atmospheric General Circulation Model), ce modèle ([17]) se couple avec un mécanisme de
chimie stratosphérique et utilise un noyau dynamique semi-Lagrangien avec des coordonnées
verticales autorisant une simulation précise des mouvements verticaux. La chimie stratosphé-
rique inclut une liste importante de composants et réactions chimiques, mais le modèle ne se
sert pas explicitement de la diffusion.
Evolution de l’Ozone constatée. Ses résultats sont similaires pour les tropiques, mais la
colonne totale d’ozone est supérieure aux observations dans les moyennes et hautes latitudes.
La chlorure est équivalente, mais se réduit plus rapidement dans le futur, ce qui conduit à une
restitution du niveau d’ozone de 1980 plus rapide.
LMDZrepro
Outils du modèle. Combinaison du GCM LMDz et du CTM REPROBUS ([18]), LMDZ-
repro est un outil très détaillé de l’Institut Pierre Simon Laplace (IPSL) de part sa chimie strato-
sphérique qui calcule l’évolution de 55 espèces à l’aide de 160 réactions gazeuses et 6 réactions
hétérogènes avec la sédimentation.
Evolution de l’Ozone constatée. LMDZrepro exhibe le plus profond trou d’ozone de CCMVal-
2 et ainsi le gradient d’ozone le plus raide au niveau du vortex polaire Antarctique. Cependant,
la réduction de l’ozone due à la chlorure est plus faible que la plupart des modèles
16](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-16-320.jpg)
![MRI
Outils du modèle. MRI emploie des coordonnées hybrides avec la pression pour diviser
l’atmosphère en 68 couches, avec une épaisseur de 500 m entre 100 et 10 hPa avec diminu-
tion sur les limites. La diffusivité horizontale permet l’implémentation de la QBO et le trans-
port d’espèces chimiques est assuré avec un schéma semi-Lagrangien hybride pour satisfaire
la continuité. La chimie stratosphérique inclut aussi les réactions hétérogènes sur les nuages
nacrés (PSCs) et les aérosols sulfatés ([19]).
Evolution de l’Ozone constatée. Ce modèle montre un biais fort pour toutes les latitudes
comparé à la colonne totale d’ozone. La hausse chlorure (importante par rapport aux autres
modèles) induit une plus forte réduction de l’ozone et donc une restitution plus lente, princi-
palement dans l’hémisphère nord (le sud rejoignant le comportement du modèle moyen). La
profondeur du trou d’ozone correspond bien aux observations, mais l’aire en est plus petite.
SOCOL
Outils du modèle. De même que E39CA, ce modèle est basé sur l’ECHAM et décrit assez
précisement la chimie stratosphérique ([20]). Il considère que toutes les espèces chimiques sont
transportées, en particulier sa précision est grande sur les ODSs, HNO3 et les particules d’acide
nitrique tri-hydratés.
Evolution de l’Ozone constatée. SOCOL est en accord avec les observations et le modèle
moyen, mais commence à montrer des biais importants au-delà de 2050 suite à un changement
de circulation qui donne naissance à un fort refroidissement dans la basse stratosphère tropi-
cale et à une réduction de l’ozone. Il montre aussi une baisse rapide de chlorure et donc une
restitution de l’ozone très rapide.
ULAQ
Outils du modèle. ULAQ est un CCM de faible résolution. Les champs dynamiques sont
tirés d’un modèle de circulation général (GCM) simplifié où les espèces de temps de vie court
et moyen sont regroupées en familles (Ox , NOy, NOx, HOx , CHOx , ... voir l’annexe au cha-
pitre ??). La distribution de taille des sulfates et des nuages nacrés est calculée en ligne en
utilisant un code de microphysique d’intéraction et de conservation de la masse pour la forma-
tion et le développement d’aérosols.
Evolution de l’Ozone constatée. Un taux faible de chlorure entraîne des colonnes faibles
pour l’ozone dans le passé. Le retour de l’ozone se fait au même moment que le modèle moyen
dans les moyennes et hautes latitudes de l’hémisphère nord, mais arrive plus tard dans les ré-
gions polaires du sud.
UMETRAC
Outils du modèle. UMETRAC part du modèle unifié (UM) et l’étend de manière verticale
en le combinant avec un progiciel de chimie stratosphérique. La chimie y est simplifiée et les
rejets de chlorure et bromure depuis les réservoirs naturels sont calculés en fonction de l’âge de
l’air.
Evolution de l’Ozone constatée. Les données d’UMETRAC n’ont pas été fournies à temps
pour juger de l’évolution de l’ozone sur CCMVal-2.
UMSLIMCAT
Outils du modèle. Ce modèle s’inspire du même UM qu’UMETRAC qu’il étend lui aussi
verticalement, mais qu’il couple avec un modèle de chimie stratosphérique où la vapeur d’eau
17](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-17-320.jpg)
![stratosphérique est liée au champ d’humidité de l’UM. Il est à noter que ce modèle inclut les
variations cycliques du rayonnement solaire.
Evolution de l’Ozone constatée. Les colonnes d’ozone sont légèrement biaisées sur toutes
les latitudes, mais la restitution se fait rapidement, en particulier dans l’hémisphère sud (faible
niveau de chlorure). Le trou de la couche d’ozone est lui bien en accord avec les observations.
UMUKCA-METO et UMUKCA-UCAM
Outils du modèle. Combinaison du modèle unifié de Met Office et de l’UKCA module de
chimie stratosphérique ([21]), UMUKCA n’utilise pas l’approximation hydrostatique, n’impose
pas de diffusion explicite. La production chimique de vapeur d’eau est ignorée dans le processus
hydrologique mais est remplacée par l’oxydation du méthane. Enfin, la vapeur d’eau est imposée
à la tropopause tropicale. Les deux modèles diffèrent sur l’utilisation de quelques données de
cinétique chimique, sur le traitement du retrait de certains composés halogénés inorganiques
dans la troposphère et sur le chauffage radiatif des aérosols stratosphériques.
Evolution de l’Ozone constatée. Pour UMUKCA-METO, le modèle est consistant avec
les observations de la colonne moyenne d’ozone dans les tropiques et les latitudes moyennes.
Une forte concentration de chlorure entraîne un grand biais sur le changement de l’ozone dans
la haute stratosphère tropicale. Dans les latitudes moyennes de l’hémisphère sud, la colonne
d’ozone se réduit après 2070. L’Arctique est raisonnablement reproduit alors que l’Antarctique
est fortement biaisé. Enfin, le trou dans la couche d’ozone au niveau de l’Antarctique est petit
et peu profond à cause d’une faible proportion de nuage nacré. Quant à UMUKCA-UCAM,
la colonne totale d’ozone est supérieure sur toutes les latitudes mais inférieure dans la haute
stratosphère. La restitution se fait au même moment que le modèle moyen sauf en Antarctique
où il se déroule plus tard. De même que son équivalent METO, le modèle montre un trou dans
la couche d’ozone au niveau de l’Antarctique plus petit et moins profond.
WACCM
Outils du modèle. WACCM est un modèle interactif complet incluant tous les paramètres
physiques de CAM et un bilan de gaz radiatifs conséquent ([22]). Il utilise aussi un noyau
dynamique unique, le chauffage chimique et par les ultraviolets extrèmes, la production de
NOx mésosphériques par les rayons solaires et cosmiques, la chimie des ions dans la basse
thermosphère. La chimie est basée sur MOZART3 et un processus de chimie hétérogène sur les
aérosols sulfatés et les nuages stratosphériques polaires a été inclus.
Evolution de l’Ozone constatée. La colonne totale d’ozone simulée par ce modèle est plu-
tôt plus faible qu’observée, sauf dans les latitudes moyennes et régions polaires. La restitution
de l’ozone au niveau de 1980 est au même moment que le modèle moyen dans l’hémisphère
sud, mais plus tôt pour l’hémisphère nord. Le trou dans la couche d’ozone en Antarctique est
similaire, mais disparaît plus vite que dans les autres modèles.
2.2 Sorties et normalisation
2.2.1 But
Le satellite AURA avec ses instruments OMI, HIRDLS, TES et MLS, ainsi que les ins-
truments GOME, GOME-2, SBUV/2 et IASI embarqués sur d’autres satellites sont autant de
moyens mis en oeuvre pour cartographier spatialement et temporellement l’ozone de l’atmo-
sphère. Afin de disposer d’une base de données comparable et valide, le meilleur moyen est de
18](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-18-320.jpg)
![normaliser le format de sortie des mesures, c’est-à-dire fournir un format commun à tous ces
instruments.
De même, pour pouvoir émettre un avis certain quant à l’évolution du climat global et ce,
jusqu’à 2100, normaliser les sorties de modèles permet de faciliter les comparaisons et les dis-
cussions autour des différents résultats. Il est aussi possible de comparer les données observées
dans le passé avec des prévisions tournées vers le passé, il s’agit alors de valider les résultats du
modèles.
Enfin, la documentation est très importante. Que ce soit sur les observations satellitaires
ou sur les modèles climatiques, il est crucial de fournir avec ces données une documentation
complète expliquant aux utilisateurs les méthodes et le parcours de ces données. C’est dans ce
cadre que rentre la fiche IASI de l’ozone, pour les données de niveau 3.
2.2.2 Résolution
Maillage horizontal
Des données réparties en grille sur une sphère peuvent être remplacées par des séries d’har-
moniques sphériques. Cela réduit à la fois la quantité de données et le temps de compilation
tout en améliorant la facilité des calculs ([23]). Les séries sont générallement tronquées en lon-
gueurs d’onde zonales (parallèle à une latitude) et méridionales (selon un méridien, parallèle
à une longitude). Deux troncatures spéciales, respectivement triangulaire et rhomboïdale, se
différencient par des longueurs d’onde zonales et méridionales respectivement identiques et as-
sociées à une constante. La troncature triangulaire est la plus souvent utilisée. Elle est aussi dite
"isotropique" du fait que chaque position et direction sur la sphère est traitée identiquement, i.e.
il y a invariance du maillage par rotation des coordonnées.
Les harmoniques sphériques sont de la forme
Ym (µ, λ) = Pm (µ)eimλ
n n
où λ représente la longitude, µ = cosφ où φ représente la latitude et m et n, indices entiers, cor-
respondant respectivement à l’indice zonal et à l’indice total avec n − |m| l’indice méridional.
On a alors m = 0, ±1, ±2, ±3, ... et n = 1, 2, 3, ... sachant que |m| ≤ n. Si M et N sont les
maximums respectifs de m et n, alors le cas M = N = r correspond au cas de la troncature tri-
angulaire, notée T (accessoirement, le cas rhomboïdal, s’identifie par N = |m| + M ). La valeur
de l’entier r indiquera le niveau de résolution du maillage. Ainsi, le modèle T106 utilise une
grille dont la résolution est de 1,21˚×1.21˚, 2,8˚×2,8˚ pour T42, etc., la résolution augmentant
avec l’entier r.
Les points obtenus peuvent être ensuite disposés sur une grille Gaussienne. Celle-ci sépare
selon latitude et longitude les points de la sphère, séparés par des distances angulaires identiques
ou non. Dans le premier cas, si la séparation angulaire est identique sur toutes les latitudes, plus
on se rapproche des pôles, plus les points seront proches physiquement parlant. C’est pourquoi
des grilles Gaussiennes réduites peuvent être utilisées : ici, le nombre de points va décroître avec
la latitude croissante pour garder une séparation physique entre chaque point similaire. Sur cette
représentation, il est à noter qu’il n’y a pas de point aux pôles (liste des grilles Gaussiennes sur
le site de l’ECMWF [24]).
Résolution verticale
Il est aussi possible de complétere le maillage horizontal par le niveau de résolution verticale
avec par exemple T159L60 où T159 correspond à la partie horizontale, et L60 à différents 60
niveaux (L pour Level).
19](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-19-320.jpg)
![La plupart des CCMs résolvent explicitement l’atmosphère terrestre depuis la surface jus-
qu’à 80 km d’altitude, avec donc la troposphère, la stratosphère et une grande partie de la mé-
sosphère. La résolution dans la troposphère est typiquement en dessous de 1 km (environ 500 m
dans la troposphère moyenne), ensuite environ 1-2 km autour de la tropopause, et une résolution
décroissante dans la stratosphère (par exemple 3-5 km dans la stratosphère moyenne). L’un des
développements actuels est l’amélioration de la résolution verticale dans la haute troposphère
et basse stratosphère (UTLS pour Upper Troposphere and Lower Stratosphere), c’est-à-dire at-
teindre 500 m de résolution autour de la tropopause. Cette région est en effet très importante
pour les systèmes climatiques de la Terre, plus particulièrement le climat en surface. Mais il
est évident que les résolutions vont dépendre des outils utilisés. Par exemple, les observations
au nadir limiteront la résolution verticale par rapport à des observations de type limb-view (le
satellite vise l’atmosphère de façon tangentielle) mais auront l’avantage de présenter moins
d’interférences vis-à-vis des nuages et une meilleure résolution horizontale.
Région de l’atmosphère
Troposphère UTLS Moyenne atmosphère
Résolution horizontale 100-300 km 100-300 km 100-300 km
Résolution verticale Colonne 2-3 km 3-5 km
troposphérique
Fréquence d’observation 3 jours 3 jours 3 jours
Période considérée 1980-2010 1980-2010 1980-2010
Précision 10-20% 8-15% 8-15%
Stabilité 4%/décennie 4%/décennie 4%/décennie
TABLE 2.1 – Résolution requise pour des observations du profil de l’ozone basée au nadir (cas
IASI) en considérant que la tropopause s’établit là où l’ozone atteint une concentration de 150
ppbv, que l’UTLS s’étend de 5 à 25 km, et qu’enfin, l’atmosphère moyenne s’étend quant à
elle de 25 à 80 km d’altitude ([25]). Les objectifs scientifiques de ces observations sont de
décrire les différences régionales de l’évolution de la couche d’ozone, de mettre en évidence
les cycles saisonniers, la variabilité interannuelle et à court terme, de caractériser le poids de
l’ozone troposphérique et enfin d’en tirer les tendances globales.
20](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-20-320.jpg)
![Chapitre 3
Mesures de l’ozone
3.1 Rappels atmosphériques
3.1.1 Les couches de l’atmosphère
L’atmosphère terrestre se décompose en 4 couches, ayant toutes des propriétés physiques et
chimiques différentes. Elles se distinguent surtout par un comportement différent de la tempé-
rature, comme l’évoque la figure 3.1 (à gauche).
La première, appelée la troposphère, est située entre 0 et 13 km (la limite supérieure variant
en fonction de la lattitude, elle est par exemple moins épaisse aux pôles avec 7 km contre 20 au
niveau de l’équateur). La troposphère contient environ 80% de la masse de l’atmosphère. Ici, la
température diminue avec l’altitude.
Ensuite, la stratosphère se caractérise par une augmentation de la température suite à la
photolyse de l’O2 par les rayons UV selon le cycle de Chapman (voir section 3.1.2). Elle se
situe entre 13 et 50 km, et possède une masse inférieure à 20% de l’atmosphère. 90% de l’ozone
atmosphérique est contenu dans la stratosphère.
Après, la stratopause, limite supérieure à la couche précédente, c’est la mésosphère. Allant
jusqu’à 90 km, cette couche voit sa température diminuer du fait que la quantité d’O2 décroît
fortement avec l’altitude. Les molécules sont de plus en plus rares et dispersées.
Enfin, au-delà de 90 km, la thermosphère, où la température croît fortement du fait du rayon-
nement solaire très intense. Cela donne des écarts de températures entre le jour et la nuit très
importants. Le maximum de température dépend ici entièrement de l’activité solaire.
Outre les kilomètres, il est possible de diviser l’altitude en fonction de la pression : on
utilise alors les isohypses de géopotentiel pour tracer les cartes de pression d’altitude. 105 Pa
correspondra alors à l’altitude du niveau de la mer : 0 km. Ensuite, la pression dépendra de la
nature des composants dans l’atmosphère, ayant une masse et une proportion différente selon les
lieux. Cependant, il est possible de moyenner l’état de l’atmosphère, c’est la base de l’altimètre
barométrique ([26]), mesurant l’altitude grâce à la pression selon l’équation suivante :
5,255
0, 0065 · h
p(h) = 1013, 25 1 − hP a (3.1)
288, 15
ou encore l’équation hydrostatique :
dp Mg
=− dz (3.2)
p RT
21](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-21-320.jpg)
![F IGURE 3.1 – Gauche : l’atmosphère terrestre et ses différentes couches (Crédit : Laurence Jac-
quenod). Droite : Les couches de l’atmosphère et la moyenne temporelle des échanges entre
elles. La différence entre hémisphère sud et hémisphère nord est assez marquante et les turbu-
lences dans la troposphère sont aussi mises en évidence.
Découpage de l’atmosphère
Pour des raisons pratiques et physiques, les calculs opérés dans les modèles climatiques se
basent sur un découpage de l’atmosphère plus ou moins consistant avec la réalité physique.
La première méthode est de séparer l’atmosphère (ou du moins sa base, c’est-à-dire la tro-
posphère et une partie de la stratosphère) en colonnes partielles. Le découpage le plus utilisé se
fait en 3 sous-colonnes : [0-6] km, [0-12] km et [0-18] km.
La seconde méthode divise aussi l’atmosphère en trois parties, mais différemment : la pre-
mière correspond à la troposphère basse, la seconde à la haute troposphère et basse stratosphère
(UTLS pour Upper Troposphere and Lower Stratosphere) en raison de l’importance chimique
que revêt cette zone, et la dernière correspond à la stratosphère moyenne.
La dernière méthode se sert de la définition de la tropopause précisée par l’ACCMIP (At-
mospheric Chemistry and Climate Model Intercomparison Project). Elle se base sur la vorticité
(ou vecteur tourbillon) potentielle, analogue au rotationnel de la vitesse et décrivant la quan-
tité de vitesse angulaire ou de rotation que subit un fluide localement. Ainsi, la tropopause est
définie comme une couche de 30 hPa centrée sur une surface de vorticité potentielle (PV pour
Potential Vorticity) de PV = 2 pvu ([27]), avec pvu étant l’unité de vorticité potentielle (pvu
pour potential vorticity unit), sachant que
10−6 K · m2
1pvu = .
kg · s
Cette définition de la tropopause permet d’éviter toutes les variations saisonnières de la hauteur
de la tropopause.
Angle zénithal solaire
L’angle zénithal solaire θz représente l’angle entre le Soleil et le zénith au point d’observa-
tion (voir figure 3.2 et la référence [28]). Il est fonction du temps, du jour de l’année et de la
latitude. Il est calculé suivant :
cos θz = sin δ sin φ + cos δ cos φ cos ω
où δ représente la déclinaison du Soleil, φ la latitude (prise comme positive dans l’hémisphère
nord) et ω l’angle horaire, mesurant l’heure locale. Il sera important par la suite pour séparer
les données jour des données nuit.
22](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-22-320.jpg)
![F IGURE 3.3 – Répartition de l’ozone dans l’atmosphère, concentré à 90% dans la stratosphère.
F IGURE 3.2 – Représentation de l’angle zénithal solaire, avec l’angle zénithal de visée (Viewing
Zenith Angle, angle entre le satellite et le zénith au point d’observation). Afin d’observer la
surface sous une incidence constante, la somme des deux angles doit être maintenue durant les
observations (Crédit : NASA).
3.1.2 L’ozone
Généralités
L’ozone est un gaz qui revêt une importance primordiale dans la troposphère. Celui-ci est
hautement nocif pour la santé humaine, toxique pour l’agriculture et très réactif. Il revêt aussi
une même importance dans la stratosphère en absorbant les rayonnements UV (A [315 ; 400] nm
et B [280 ; 315] nm). Ce bouclier anti-UV est cependant vulnérable à la destruction catalytique
par des composés halogènes comme par exemple des CFCs. Son rôle dans le forçage radiatif
est différent dans les deux couches atmosphériques concernées : positif dans la troposphère et
négatif dans la stratosphère, mais en moindre proportion. L’ozone troposphérique est produit de
l’oxydation du CO, des COVs (Composés Organiques Volatils) et des hydrocarbones par OH
en présence des NOx tandis que l’ozone stratosphérique provient majoritairement du cycle de
Chapman (années 1930) :
O2 + hν → 2O O + O3 → 2O2
Formation Destruction
O + O2 + M → O3 (+ chaleur) O3 + hν → O + O2 (+ chaleur)
Il existe deux méthodes pour observer l’ozone de l’atmosphère. La première, dite passive, uti-
lise la radiométrie ou la spectrométrie. Cela consiste à observer le rayonnement solaire (soit
23](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-23-320.jpg)
![UV, IR ou micro-onde) de façon verticale (au nadir ou légèrement décalé) ou aux limbes (atmo-
sphère observée par strates). La seconde, active, nécessite l’envoi d’un rayonnement, comme le
LIDAR, afin de caractériser les particules rencontrées sur le chemin optique. Cependant pour
des raisons de puissance, de stabilisation entre autres, cette technique est surtout utilisée au sol.
Unité Dobson vs ppm
Le Dobson est l’unité de mesure évaluant la quantité d’un composant (ici l’ozone) sur toute
la verticale d’un point donné de la surface terrestre ([29]). Cette unité est très utile dans le cas de
mesures satellitaires ou se basant sur des techniques usant un long parcours optique avec le So-
leil ou la Lune comme source de fond. Ainsi, il est mesuré l’abondance d’un composant dans la
colonne verticale à un endroit spécifique où la résolution dépendra de l’aire sur laquelle la me-
sure s’effectue. Ces "colonnes d’abondance" ont l’unité de quantité/nombre de molécules/masse
par unité d’aire. Une fois converti, 1 DU (Dobson Unit) correpond à l’épaisseur en unité 10-3 cm
que la colonne d’ozone occuperait si elle était compressée dans une couche de densité uniforme
à 273.15 K et une atmosphère (105 Pa). 100 DU sont alors équivalents à 1 mm d’ozone pur au
niveau de la mer. Pour une colonne d’ozone type, on obitent des mesures d’environ 300 DU
pour des extrèmes allant de 250 DU (au niveau des régions équatoriales) jusqu’à 500 DU (dans
les régions polaires au printemps).
A contrario d’une mesure en Dobson effectuée sur toute une colonne, les concentrations
en ppm ou VMR (pour Volume Mixing Ratio) sont plus utilisées dans les reflexions et plus
compréhensibles au grand public. Elles correspondent à une fraction à laquelle contribue une
substance sur la totalité de l’échantillon. Ainsi, 1 ppm d’O3 (pour partie par millions) correpon-
dra à 10-6 m3 d’O3 par m3 d’air, 1 ppb à 10-9 , etc. Il est de même possible de les transcrire en
kg, mol, ... .
Pour faire la conversion entre données en ppmv et données en Dobson, il faut se servir d’un
paramètre supplémentaire : la pression. Dans la suite, certains jeux de données sont en ppmv
alors que le choix s’est porté sur des colonnes partielles et totales. Ainsi, la conversion s’effectue
suivant l’équation suivante :
j
1 MO3
(O3 )j [DU] = (O3 )i [ppmv] ∗ 10−6 ∗ (Pi − Pi+1 ) ∗ ∗ ∗f (3.3)
i=0
g Mair
où (O3 )i en [DU] est la colonne partielle i en Dobson, Pi et Pi+1 sont les niveaux de pression des
niveaux i et i + 1, g l’accélération en [m/s2 ], MO3 et Mair les masses volumiques respectives de
l’ozone et de l’air, f = 46641.59 facteur de conversion entre les kg/m2 et le Dobson. Ce facteur
est basé sur la définition du Dobson comme étant 2, 89 · 1016 molécules/cm2 ([6]). Il faut ensuite
faire cette somme sur tout le profil de la colonne pour arriver à la colonne totale.
3.2 Mesures IASI
3.2.1 Rappels théoriques
Dans l’atmosphère, les molécules peuvent absorber des radiations électromagnétiques qui
vont modifier de façon différente suivant l’énergie la configuration de la molécules. Dans le
cas de radiations micro-ondes, l’énergie de rotation de la molécule sera modifiée, le niveau
d’énergie va changer, c’est une transition rotationnelle. Dans le cadre de radiations infrarouges
(de longueur d’onde comprise entre 2,5 et 25 µm), ce sera au tour de l’énergie de vibration, ce
sera alors une transition vibrationnelle, base de la spectroscopie infrarouge. Enfin, s’il s’agit du
visible ou de l’ultraviolet (entre 10 et 700 nm), l’énergie électronique sera modifiée impliquant
24](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-24-320.jpg)
![F IGURE 3.4 – Spectre en radiance IASI normalisé et ses bandes spectrales (Crédit : Eumetsat).
les transitions électroniques, qui sont elles à la base de la spectroscopie d’absorption UV-visible.
L’énergie totale de la molécule est donnée par la somme de ces trois énergies.
Spectroscopie Infrarouge
Ainsi, en observant le rayonnement infrarouge d’un gaz, il est possible d’en déduire les
vibrations caractéristiques pour remonter aux molécules composant ce gaz. Ces molécules ab-
sorbent les radiations infrarouges comprises entre 400 et 4000 cm-1 et montrent un Dirac à la
fréquence de la vibration. Ce Dirac sera élargi suivant la pression et la température. À basse
pression (haute altitude), la raie subira un élargissement Doppler, car la vitesse des particules
sera élevée. A contrario , à haute pression (basse altitude) règnent les collisions entre les parti-
cules du fait de leur nombre. On parle alors d’effet Lorentz.
De même, autre facteur de la spectroscopie infrarouge, la polarisation de la molécules. Ce
facteur agira sur l’intensité de la raie, qui va croître avec la polarité. Derniers facteurs à prendre
en compte, les masses des atomes et leurs forces de liaison joueront sur la fréquence de l’os-
cillation. La figure 3.4 montre le spectre en radiance IASI normalisé et décomposé selon les
différentes bandes le constituant.
La grande difficulté consiste à les interpréter en prenant en compte tous les effets de l’atmo-
sphère. Pour cela, on procède à un processus d’inversion, qui consiste à retrouver les différents
profils de température, de pression, de gaz et d’aérosols dans la zone observée afin d’obtenir au
final les données des quantités de molécules dans leur intégralité.
3.2.2 Création des fiches IASI
Pourquoi ?
Avant de traiter les données IASI, il m’a été demandé de créer une fiche IASI. Dans le cadre
du ESA-CCI (Climate Change Initiative for ESA), 10 variables essentielles au climat (ECV
pour Essential Climate Variable) ont été sélectionnées parmi la quarantaine existante ([25]). Sur
25](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-25-320.jpg)
![ces 10, 3 concernent le milieu marin, 3 les milieux surfaciques et enfin, 4 pour l’atmosphère :
les nuages, les aérosols, l’ozone et les GES (sachant que l’ECV sur l’ozone se divise en 3
parties : le profil au nadir, les limbes et la colonne totale). Un consortium par ECV, regroupant
des spécialistes du climat mais non des modèles, a été choisi afin de répertorier, transcrire et
valider les données sous un format qu’on pourrait décrire comme étant universel. Parallèlement,
un groupe a été monté, le CMUG (Climate Modeling User Group), dans le but de valider les
précisions (important pour les modèles), les modes, les origines des mesures et in fine, de fournir
la description du format des instruments ([30]). NetCDF CFcompliant ([31]) est le format retenu
par la communauté internationale.
À l’intérieur de ce format est inclus toute la description de la prise des mesures, permettant
aux groupes voulant utiliser les modèles de valider les résultats qu’ils obtiennent. C’est donc un
format de données "auto-documenté" créé par le Unidata program de l’University Corporation
for Atmospheric Research (UCAR).
Le modèle de données netCDF classique est divisé en 3 parties : variables, dimensions et
attributs. Les variables consistent en un tableau de données de N-dimensions pouvant être soit
de type char, byte, short, int, float ou double. Les dimensions décrivent les axes des tableaux de
données. Chaque dimension possède un nom et une longueur, cette dernière pouvant être étirée
au bon vouloir de l’utilisateur. Enfin les attributs annotent les variables ou les fichiers avec des
petites notes ou des données supplémentaires, de préférence de taille réduite.
La fiche
L’annexe au chapitre C comprend la note technique retenue pour l’instrument IASI, mais
pour un produit de l’instrument : l’ozone. En effet, il a été demandé pour le CMIP5 de consa-
crer une fiche par produit, impliquant quelques redondances pour par exemple, la description
du satellite. Chaque fiche se divise en plusieurs parties : une partie introductive explicitant l’in-
tention de la fiche, la description des données, leur origines, leurs validations. La fiche doit être
assez complète pour que tout utilisateur puisse comprendre la provenance des données, mais
elle doit être en même temps assez claire pour permettre aux non-initiés de l’instrument de
saisir les principales caractéristiques des données.
3.2.3 Les données et leurs récupérations
Les données issues du satellite Metop sont réceptionnées à la station Svalbard (Norvège) qui
les traite et peut les transmettre environ 2h15 après acquisition (pour le niveau brut). À l’aide
des satellites de télévision (le Digital Video Broadcast (DVB)), les données sont acheminées par
le système EUMETCast (EUMETSAT’s Data Distribution System) sur une zone géographique
regroupant la totalité de l’Europe et certaines régions de l’Afrique. Les formats sont variés,
incluant les formats primaires de l’EPS mais aussi ceux du WMO : BUFR (Binary Universal
Form for the Representation) et GRIB (GRIdded Binary). Outre l’envoi, les archives sont elles
aussi disponibles sur l’EUMETSAT Data Centre.
Les données récupérées correspondent aux années 2008 et 2009. 2 ans de données per-
mettront une statistique globale. Les premiers mois récupérés sont les mois d’août et septembre
2008. En effet, fin août de cette année là, un trou est apparu dans la couche d’ozone au niveau de
l’Antarctique. Nous pourrons alors voir l’effet sur les confrontations et comparaisons. De plus,
l’année 2008 est considérée comme une année phare pour le projet CCI de l’ESA. Sur cette an-
née, le but est de rassembler le plus grand nombre de d’ECVs caractérisables disponibles dans
le but d’avoir une référence sur le processus d’action.
26](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-26-320.jpg)
![La chaîne du niveau 1
Par rapport à la donnée brute observée (niveau 0), le satellite opère dès la mesure une cali-
bration afin d’obtenir un produit de niveau supérieur (voir l’annexe 2 au chapitre B pour la liste
des niveaux des produits IASI). À bord du satellite, les spectres subissent déjà une calibration
radiométrique. Ici, une approximation dépendant de la longueur d’onde est appliquée pour relier
la luminance énergétique du corps noir B(λ,T) à λ et T suivant la loi de Planck :
C1
B(λ, T ) = W · m−2 · µm−1 · sr−1 (3.4)
λ5 [exp(C2 /λT ) − 1]
avec C1 = 1, 1910659 · 10−8 W·m-2 ·sr-1 ·cm4 et C2 = 1.4388 cm·K. Ensuite, de nouvelles
fonctions de Planck sont calculées pour apporter une correction appropriée aux spectres (via une
chaîne de calcul dite ISRFEM). De même, les contributions de la radiance réfléchie, l’impact du
miroir à différents angles, sa dépendance vis-à-vis de la température et la géolocalisation sont
pris en compte.
Les données arrivent alors au niveau 1b, où les spectres 1a vont être suréchantillonnés d’un
facteur 5 à l’aide de transformées de Fourier. Les spectres sont aussi interpolés sur une nouvelle
grille équidistante suivant l’interpolation cubique (spline).
Enfin, le spectre est apodisé à l’aide des fonctions d’apodisation interpolées dans la chaîne
ISRFEM. On effectue la convolution dans l’espace de l’interférogramme suivant
spectre apodisé = TF−1 [fonction d’apodisation × TF(spectre 1b)]
L’analyse des radiances dans les FOV (Field of View, ou champ de vue) du sondeur, en terme de
classification de surfaces radiatives (étendues, température, structure) est aussi effectuée ame-
nant au produit IASI de niveau 2.
Données EUMETSAT IASI-L2
Le format typique des données EUMETSAT de niveau 2 sont de la forme suivante
iasi_yyyymmdd_hhmmss_metopa_nnnnn_eps_o_<product code>.l2_bufr où yyyymmdd cor-
respond à l’année, le mois et le jour au Temps Universel Coordonné (UTC), hhmmss pour
heures, minutes et secondes à partir du début de prises de données, nnnnn est le nombre ortibal
et enfin <product code> = ’twt’ pour la température atmosphérique et la vapeur d’eau, ’ozo’
pour l’ozone atmosphérique (notre cas), ’trg’ pour les gaz traces, ’ems’ pour l’émissivité et
enfin ’clp’ pour les paramètres des nuages.
Une journée de donnée est répartie en plusieurs fichiers correspondant aux parties d’orbites.
Ainsi, une journée se divise en plus ou moins 14 fichiers de taille environnant les 65 Mo. Ce qui
fait pour une journée complète pas moins de 900 Mo de données à traiter.
Données LATMOS-ULB
Les données IASI provenant du LATMOS-ULB sont de la forme suivante (voir tableau 3.1)
sous un nom de type IASI_LATMOS_ULB_O3_20080816.tar. Le jour a été divisé en plusieurs
fichiers correspondant à des orbites. Le nom du fichier est alors du type IASI_O3_AK_20080816_*.txt
et chaque fichier .txt a une taille oscillant autour de 600 Mo. Une fois ouvert, chaque ligne cor-
respond alors à un point. La matrice du noyau est calculée en colonne partielle, sur 40 niveaux.
Le premier niveau correspond à la première couche de l’atmosphère [0-1] km, le niveau 2 à [1-
2] km, ..., le niveau 40 correspondra lui à [39-sommet de l’atmosphère] km. Lorsque le premier
niveau n’est pas disponible (à cause de l’orographie, c’est-à-dire là où l’altitude est supérieure
au premier point de mesure, voire aux niveaux suivants), la donnée est imposée à -999.
27](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-27-320.jpg)
![LATMOS-ULB 1 latitude
2 longitude
3 temps [hhmmss]
4 SZA [˚]
5 à 44 profil de l’ozone [ppb] sur 40 niveaux
45 à 84 erreur sur le profil [%] sur les 40 niveaux
85 à 1684 matrice (40 × 40) du noyau
TABLE 3.1 – Format des données IASI fournies par le LATMOS-ULB. Chaque ligne correspond
à un point.
Le LATMOS-ULB se base sur les donnée de l’instruement IASI à bord de METOP. Ainsi,
provenant de la même source que les données d’EUMETSAT, elles sont sensiblement simi-
laires. Cependant, le LATMOS-ULB utilise une méthode de récupération différente. Eumetsat
utilise un réseau de neurone alors que le LATMOS-ULB se base sur une optimisation numé-
rique inspirée de la méthode d’estimation optimale (OEM, [32]). Cette dernière méthode permet
de fournir des estimations des erreurs, ce qu’Eumetsat via les réseaux de neurones ne peut pas
faire.
Autre différence entre les deux jeux de données, le LATMOS-ULB utilise un masque nua-
geux moins strict qu’EUMETSAT. Ainsi, il dispose d’un nombre supérieur de données, mais
cela peut avoir une influence sur les valeurs de l’ozone qui seront alors retournées.
Données MIPAS
Le Michelson Interferometer for Passive Atmospheric Sounding (MIPAS), via l’Institut für
Meteorologie und Klimaforschung/Instituto de Astrofísica de Andalucía (IMK/IAA), a rendu
possible la comparaison des données IASI avec un autre satellite (MIPAS étant embarqué sur
Envisat et opérationnel depuis 2002). Il fournit des profils d’ozone (et température) dans la
stratosphère avec une résolution verticale de 3 à 5 kilomètres. Téléchargeable sur le serveur de
l’IMK, les données sont présentées sous la forme MIPAS-E_IMK.20080816.V4O_O3_202 et
une routine IDL (Interactive Data Language) est fournie pour lire les fichiers. Chaque fichier
correspondra à une journée et à l’intérieur, chaque paragraphe correspondra à une valeur de
latitude/longitude. Ensuite, les données sont présentées sous la forme de 8 colonnes (voir ta-
bleau 3.2). Il y a environ plus de 1000 géolocalisations par jours, ce qui ne peut certainement
pas remplir une grille de 0.5˚× 0.5˚(∼ 260 000 points), ni même 1˚× 1˚(∼ 65 000 points). Il faut
alors soit interpoler sur une grille d’environ 10˚× 10˚, soit prendre une moyenne sur plusieurs
jours.
La couverture journalière selon les années est disponible sur le site suivant :
http://www-imk.fzk.de/asf/sat/envisat-data/O3.html
Il permet alors de voir la qualité des données sur les différentes années d’activité du satellite et
suivant les différents traitements opérés.
Les données qui nous intéressent sont fournies en [ppmv]. À l’aide de la pression elle aussi
fournie, il est alors assez aisé de convertir les concentrations en colonnes partielles (équa-
tion 3.3) pour ensuite les comparer aux colonnes partielles d’EUMETSAT.
Données CNRM
Le Centre National de Recherches Météorologiques (CNRM) a pour but d’améliorer la
connaissance de l’atmosphère et de ses interfaces afin de mieux comprendre et modéliser les
28](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-28-320.jpg)
![MIPAS 1 flag de visibilité : 0 si l’altitude non visible pour MIPAS, 1 sinon
2 altitude [km]
3 pression [hPa]
4 température [K]
5 extraction de la cible en vmr [ppmv]
6 déviation standard du bruit de l’erreur [ppmv]
7 entrée diagonale de la matrice du noyau [-]
8 résolution verticale [km]
TABLE 3.2 – Format des données MIPAS provenant de l’IMK. Chaque point de l’espace aura
ces 8 colonnes et ∼60 lignes. Latitude et longitude se récupèrent en en-tête des colonnes (voir
annexe D).
processus qui régissent leur évolution et donc la prévision du temps et l’évolution du climat.
L’équipe CAIAC au sein du CNRM m’a fourni les sorties du modèles CNRM-CCM. Sous un
format NetCDF, elles compilent une année type, avec une grille par jour, de 2.8125˚×2.8125˚×
71 niveaux en altitude. Les données sont en [ppm] et afin de les convertir en Dobson (via l’équa-
tion 3.3), l’équipe CAIAC a fourni aussi l’équivalent pression, établi sur une grille strictement
identique.
Il faut bien avoir en tête qu’il s’agit d’une année modélisée et non des mesures. Ainsi une
comparaison pixel par pixel, ou plutôt maille de grille par maille de grille n’a pas de sens.
29](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-29-320.jpg)



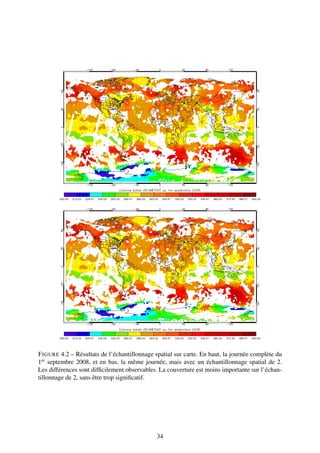
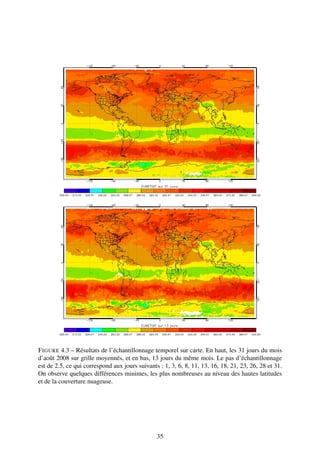
![4.3 Confrontation aux données LATMOS-ULB
La confrontation aux données issues de l’extraction du LATMOS-ULB est importante. Non
seulement elle permet d’avoir un oeil critique sur l’extraction d’EUMETSAT, récemment im-
plémentée, mais elle permet aussi de quantifier les erreurs d’EUMETSAT. En effet, ces derniers
utilisent un réseau de neurones (voir section 6.3.1) pour remonter aux valeurs en ozone alors
que le LATMOS-ULB se base sur la méthode d’estimation optimale. À l’aide de cette méhode,
le LATMOS-ULB quantifie son erreur. Ainsi, confronter EUMETSAT au LATMOS-ULB per-
mettra d’estimer une erreur sur ce produit.
4.3.1 Lissage des données.
Dans le but de comparer ce qui est comparable, les données du LATMOS-ULB ont été
fournies avec leur averaging kernels (AK). Il a été montré ([42]) qu’une comparaison directe
de profils d’ozone (ou tout autre variable atmosphérique) pouvait conduire à des résultats non
satisfaisants. Ainsi, il faut procéder à un lissage des données.
Les AKs du LATMOS-ULB se présentent comme une matrice 40×40 (cf tableau 3.1), pour
les 40 niveaux décrits. Il y a donc une matrice complète par point. Ensuite, à l’aide du profil
apriori, il est possible d’obtenir le profil d’ozone lissé, qui sera à comparer avec les données du
LATMOS-ULB. En effet, c’est aux profils d’EUMETSAT ou de tout autre jeu de données qu’il
faut appliquer le lissage du LATMOS-ULB pour permettre la comparaison entre les deux.
Le lissage s’effectue en suivant l’équation suivante :
Xlissé = A · Xr + (I40 − A) · Xa
où Xr est le profil en colonnes partielles à lisser, A la matrice AK IASI et Xa le profil apriori
IASI, lui aussi en colonnes partielles. Il faut faire très attention aux unités, et penser à les
convertir - ou non - au préalable.
Dans notre cas, les données d’EUMETSAT, qui vont etre comparées aux données LATMOS-
ULB sont fournies en colonnes partielles, au nombre de 3 et une colonne totale. Il est donc
impossible d’utiliser le lissage. Les comparaisons seront alors directes. Ce n’est pas parfait, mais
cela a du sens. Pour les colonnes totales, le contenu étant intégré, les différences de sensibilité
dans les couches de l’atmosphère sont estompées.
4.3.2 Problème de pression...
Les données fournies par EUMETSAT et qui sont à la base du travail sont en colonnes
partielles, plus exactement en kg/m2 . Pour une meilleure clarté, ces données ont été converties
en Dobson (facteur f de l’équation 3.3). Les données du LATMOS-ULB, quant à elles, sont
fournies en ppm. Il faut donc utiliser la pression. Cependant, le LATMOS-ULB ne fournit pas la
pression avec les concentrations. La conversion entre altitude et pression s’opère alors suivant
l’équation 3.1. Cependant, cette équation est vrai en partie pour la troposphère, mais diverge
rapidement -mathématiquement parlant- au delà de 35 km. Ainsi, en me basant sur le travail de
la NACA ([26]), l’équation de la pression
5,255
0, 0065 · h · 103
p(h) = 101325 1 − Pa (4.1)
288, 15
pour les premiers kilomètres est couplée avec
h − ht
p(h) = p(ht ) · exp − (4.2)
8.4
36](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-36-320.jpg)
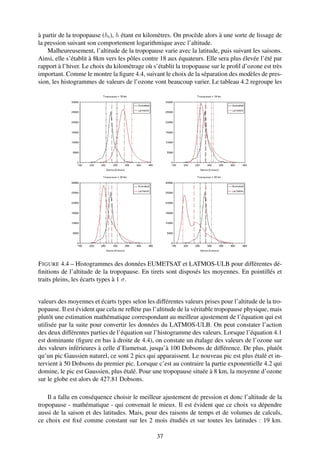
![ht [km] x [Dobson]
¯ σ [Dobson] Nombre de points
EUMETSAT / 284.59 23.74 181974
8 427.81 39.63 302765
15 337.14 32.07 302765
LATMOS-ULB 19 282.33 34.21 302765
20 271.12 36.33 302765
30 233.90 47.42 302765
TABLE 4.2 – Statistiques suivant l’altitude de la tropopause ht mathématique pour le 1er sep-
tembre 2009. Sont regroupés ici la moyenne x, l’écart-type σ, et le nombre de points utilisés.
¯
Dès lors, l’équation de pression qui permet de transcrire les données du LATMOS-ULB en
unités Dobsons est définie, tout en gardant en tête qu’on dispose ici d’une source d’erreur non
négligeable.
4.3.3 Cas général
Dans la partie qui suit, le code de couleur suivant est adopté : les données issues d’EUMETSAT
seront en noir, alors que celles provenant du LATMOS-ULB seront en rouge (à l’exception faite
des nuages de points où la courbe en rouge représente la courbe de régression linéaire associée
au nuage et des comparaisons entre données d’EUMETSAT). De même, les données issues de
MIPAS seront en bleues et celles du CNRM en vertes.
J’utilise par la suite un code de couleur (figure 4.5). La table IDL 26 est utilisée pour les
cartes représentant les valeurs réelles de l’ozone, pour les colonnes partielles et/ou totale. La
table IDL 33 est quant à elle utilisée pour les cartes représentant des différences d’ozone.
F IGURE 4.5 – Tables des couleurs utilisées : celle du haut (table IDL 26) correspond à une
représentation directe des valeurs d’ozone (le plus souvent en Dobson, allant de 200 à 400
Dobsons pour la colonne totale), et celle du bas (table IDL 33) correspondant à la différence
entre deux jeux de données, aussi en unité Dobson.
Pour faire une comparaison directe au premier abord, les couples [latitude,longitude] iden-
tiques pour les données d’EUMETSAT et du LATMOS-ULB sont sélectionnés, puis on observe
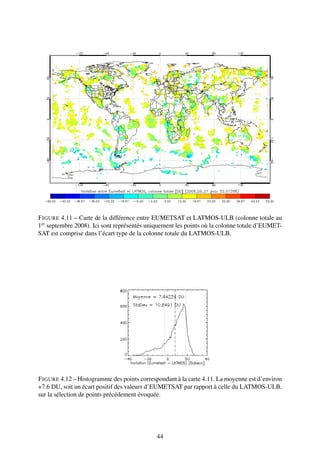
la différence. Pour le 1er septembre 2008, la moyenne générale des données d’EUMETSAT pour
la colonne totale est de 284.44 Dobsons et pour les données du LATMOS-ULB, 286.57, soit
un écart relatif de +0.74%, ce qui est assez bon. Sur tout le mois de septembre, l’écart relatif
absolu moyenné est de 1.78% avec au maximum un écart de -5% pour le 22 septembre. Ce sont
des résultats très bons, qu’il faut coupler avec le fait que le choix de la hauteur de la tropopause
n’y est pas étranger car ce choix s’est basé sur la moyenne globale.
Lorsqu’on regarde la figure 4.6, dont l’écart relatif est de +0.74%, on constate que les dif-
férences se situent principalement près des pôles. En l’occurence, il y a un fort écart entre
38](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-38-320.jpg)
![les données EUMETSAT et LATMOS-ULB en dessous de -60˚ de latitude. Ces dernières sont
nettement supérieures aux données d’EUMETSAT de l’ordre de 25%, alors qu’a contrario, EU-
METSAT est supérieur à LATMOS-ULB d’environ 3% sur les latitudes supérieures à 60˚.
F IGURE 4.6 – Différence sur les points identiques des valeurs issues d’EUMETSAT et du
LATMOS-ULB pour une journée (2008_09_01). Seuls les points possédant le couple [longi-
tude,latitude] strictement identique ont été sélectionnés. En effet, les données provenant du
LATMOS-ULB et d’EUMETSAT sont issues du même satellite, et donc les coordonnées de-
vraient correspondre. Cependant, puisque les deux laboratoires procèdent à un retrieval différent
et ont des flags nuageux variables, celles-ci peuvent varier.
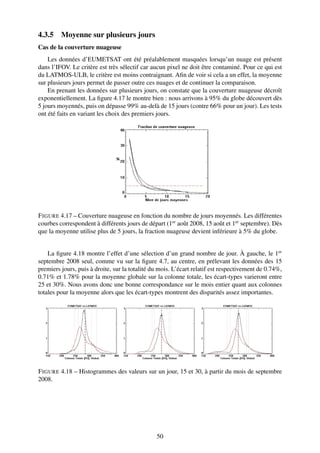
On peut tracer les histogrammes des valeurs des colonnes totales d’ozone pour les deux
jeux de données. Pour la même journée que la figure 4.6, on observe bien sur la figure 4.7
l’importante différence au niveau du pôle Sud. L’écart relatif de -25% entre EUMETSAT et
LATMOS-ULB sur les latitudes inférieures à -60˚ tombe à -18% pour les latitudes inférieures à
-45˚. Quant aux autres latitudes, la différence tourne autour de +4%.
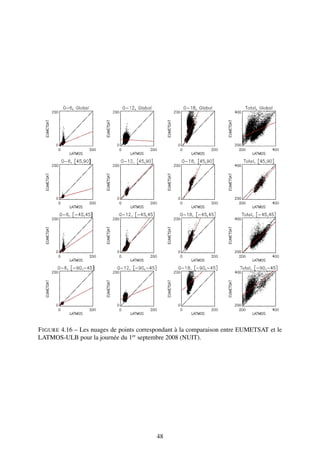
Dès lors qu’on s’intéresse aux colonnes partielles plutôt que la colonne totale, là aussi
quelques différences sont à noter. Pour ce qui concerne la colonne [0-6] km, on observe à partir
de la figure 4.8 en haut à gauche une très faible variation des valeurs (qui tient aussi du fait que
les valeurs elles-mêmes sont faibles). Cependant, l’écart relatif sur le globe est de -29% (diffé-
rence de 6 Dobsons). Ensuite, la colonne [0-12] km (en haut à droite) commence à développer
l’écart au niveau du pôle Sud alors que le reste correspond assez bien. Ici, l’écart relatif est de
4% pour une différence de 1 Dobson. La colonne [0-18] km est très différente entre EUMET-
SAT et LATMOS-ULB. Ici, les données LATMOS-ULB sont bien plus importantes, et ce, sur
la totalité du globe, l’écart relatif est très important : 75%. Enfin la colonne totale, identique à
la figure 4.6 avec l’important écart au niveau du pôle Sud. De l’importante différence pour la
colonne [0-18] km, nous pouvons tirer une information sur le profil d’EUMETSAT par rapport
à celui du LATMOS-ULB. En effet, entre 12 et 18 km, le profil d’ozone s’accroît bien plus ra-
pidement pour les données du LATMOS-ULB par rapport à celles d’EUMETSAT. Nous avons
39](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-39-320.jpg)
![F IGURE 4.7 – Histogrammes des valeurs des colonnes totales d’ozone entre EUMETSAT (noir)
et LATMOS-ULB (rouge) pour le 1er septembre 2008. En haut à gauche, sur la totalité du globe,
à droite, pour les latitudes inférieures à -45˚, en bas à gauche, entre -45˚ et 45˚, et à droite, pour
les latitudes supérieures à 45˚.
entre 12 et 18 km respectivement +47 Dobsons contre +13 pour la journée du 1er septembre
2008, tendance qui se vérifie tout au long du mois. L’écart entre colonnes partielles peut trou-
ver son origine dans l’équation de la pression. En effet, l’équation 4.1 utilisée peut mésestimer
les ∆p de l’équation de conversion 3.3 par rapport à la réalité et donc surestimer les valeurs
d’ozone converties. Cela reste à vérifier en modifiant l’équation et en constant la répercussion
sur la colonne [0-18] km.
En opérant une sélection de longitudes (ici entre 40˚ et 45˚) et en répartissant suivant la
latitude les valeurs d’ozone, on obtient la figure 4.10 où on constate l’écart existant sur les
basses latitudes (au delà de -45˚). La colonne 0-18 km montre l’écart le plus important hors des
latitudes allant de -25˚ à 50˚. Seule la colonne totale est en accord sur les latitudes moyennes
et supérieures. En effet, pour les colonnes partielles, les valeurs d’ozone d’EUMETSAT sont
rarement comprises dans l’intervalle formé par les valeurs du LATMOS-ULB plus ou moins
l’erreur.
Dans le cadre où l’on sélectionne les valeurs d’ozone d’EUMETSAT correspondant aux
valeurs du LATMOS-ULB plus ou moins l’erreur, on montre que pour le 1er septembre 2008,
un peu plus de 50% des valeurs sont retenues (exactement 52.5% pour ce jour-ci). La figure 4.11
représente la différence entre EUMETSAT et le LATMOS-ULB pour ces 52.5%. On constate
que la plupart des points situés au sud de -60˚ de latitude ont été évincés (en comparaison avec
la figure 4.6). La figure 4.12 quant à elle représente l’histogramme des points correspondant à
la carte 4.11.
40](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-40-320.jpg)
![F IGURE 4.8 – Cartes des différences entre EUMETSAT et LATMOS-ULB pour les 3 colonnes
partielles et la colonne totale (valeurs allant de -50 à + 50 Dobson). En haut à gauche, la colonne
partielle [0-6] km. En haut à droite, la colonne partielle [0-12] km. En bas à gauche, la colonne
partielle [0-18] km puis enfin la colonne totale en bas à droite, similaire à la figure 4.6.
0-6 km 0-12 km 0-18 km Col. tot.
Global Coeff. corr. 0.39 0.26 0.73 0.49
57483 pts Coeff. dir. 0.39 0.28 2.23 0.53
Ord. origine 7.37 25.58 -34.43 128.57
Lat [45˚,90˚] Coeff. corr. 0.34 0.48 0.79 0.80
14526 pts Coeff. dir. 0.38 0.90 1.85 1.04
Ord. origine 8.56 9.51 -15.16 -30.16
Lat [-45˚,45˚] Coeff. corr. 0.59 0.75 0.87 0.68
33315 pts Coeff. dir. 0.70 1.22 2.02 0.85
Ord. origine -0.38 -15.20 -38.22 21.14
Lat [-90˚,-45˚] Coeff. corr. 0.52 0.15 0.26 0.71
9642 pts Coeff. dir. 0.42 0.28 0.95 0.70
Ord. origine 8.22 39.55 79.63 119.08
TABLE 4.3 – Coefficients de corrélations, coefficients directeurs et ordonnées à l’origine as-
sociés aux nuages de points de la figure 4.9, pour le 1er septembre 2008. On distingue assez
facilement les valeurs où la corrélation est faible (loin des latitudes moyennes).
41](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-41-320.jpg)
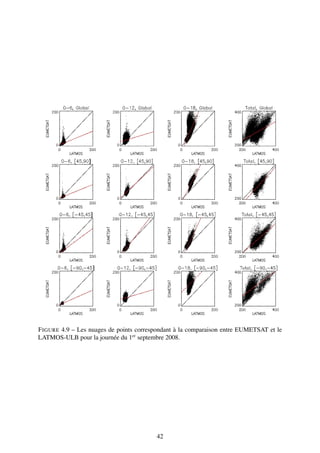
![F IGURE 4.10 – Sélection sur des longitudes comprises entre 40 et 45˚ des valeurs d’ozone selon
les latitudes. En haut, pour les colonnes partielles [0-6], [0-12] et [0-18] km, en bas, sur toute la
colonne totale.
Conclusion à mi-parcours
En considérant le profil de pression comme constant sur la surface du globe, on procède
à une forte simplification qui n’est pas satisfaisante pour établir l’erreur du produit EUMET-
SAT. Puisque que la pression a été calculée à partir de la moyenne globale, les extrema et
fluctuations présentent des erreurs importantes (comme c’est le cas pour les hautes latitudes).
Afin d’améliorer l’estimation des données LATMOS-ULB, il est possible d’en sélectionner les
points communs avec les données d’EUMETSAT et d’utiliser les profils de pression calculés à
partir des profils de température qui sont fournis par EUMETSAT. Les résultats sont présentés
à partir de la section 4.4.
43](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-43-320.jpg)
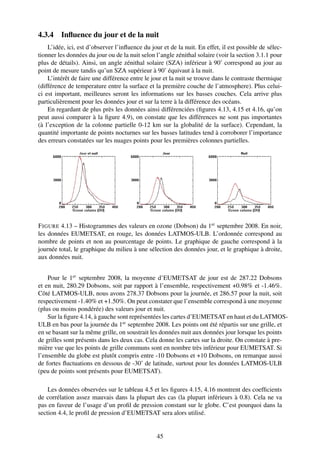
![0-6 [km] 0-12 [km] 0-18 [km] Col. Tot.
Ensemble 20.90/15.43 35.03/36.52 47.90/80.45 284.44/282.34
Jour 21.56/15.93 35.96/36.68 48.92/77.43 287.22/278.39
Nuit 19.80/14.88 33.43/36.34 46.17/83.68 280.29/286.57
TABLE 4.4 – Colonnes partielles et totale (en DU) du 1er septembre 2008 (en noir, EUMETSAT
et en rouge, LATMOS-ULB) et leurs séparations en données jour et nuit.
F IGURE 4.14 – À gauche, cartes EUMETSAT et LATMOS-ULB des valeurs en ozone du 1er
septembre 2008 (échelle de 200 à 400 Dobsons). À droite, cartes des différences entre le jour et
la nuit (jour - nuit, pour une échelle de -50 à +50 Dobsons).
Dans la suite, la différence entre le jour et la nuit ne sera pas explicitée. Il serait néanmoins
intéressant d’effectuer a posteriori les mêmes calculs qu’ensuite en séparant le jour de la nuit,
tout en gardant en tête que le nombre de points sera réduit de moitié.
46](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-46-320.jpg)
![DONNÉES JOUR
DONNÉES NUIT 0-6 km 0-12 km 0-18 km Col. tot.
Global Coeff. corr. 0.39/0.41 0.50/0.01 0.89/0.59 0.67/0.36
34214 pts Coeff. dir. 0.44/0.38 0.94/-0.05 2.47/2.13 0.81/0.42
21791 pts Ord. origine 5.99/7.76 0.44/37.92 -53.60/-20.71 40.27/166.81
Lat [45˚,90˚] Coeff. corr. 0.37/0.27 0.49/0.38 0.79/0.73 0.78/0.81
11519 pts Coeff. dir. 0.40/0.27 0.85/1.04 1.82/1.89 1.03/1.06
2291 pts Ord. origine 8.21/10.87 11.18/3.19 -13.54/-20.54 -26.07/-33.44
Lat [-45˚,45˚] Coeff. corr. 0.63/0.53 0.77/0.73 0.88/0.87 0.63/0.74
20294 pts Coeff. dir. 0.76/0.64 1.24/1.22 1.98/2.06 0.79/0.89
13021 pts Ord. origine -2.11/1.32 -16.54/-14.08 -37.61/-37.90 43.39/21.52
Lat [-90˚,-45˚] Coeff. corr. 0.01/0.67 0.10/0.25 0.54/0.22 0.79/0.69
2401 pts Coeff. dir. 0.15/0.50 0.23/0.40 1.76/0.86 0.73/0.75
6479 pts Ord. origine 12.40/7.29 37.94/37.14 25.29/87.56 100.82/109.56
TABLE 4.5 – Coefficients de corrélations, coefficients directeurs et ordonnées à l’origine asso-
ciés aux nuages de points de la figure 4.15 et 4.16, pour le 1er septembre 2008, séparé en données
jour (noir) et données nuit (bleu). On distingue assez facilement les valeurs où la corrélation est
faible (loin des latitudes moyennes).
49](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-49-320.jpg)
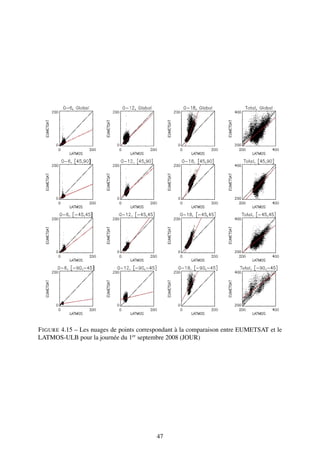
![4.4 Nouvelle confrontation aux données LATMOS-ULB
Afin de convertir en colonnes partielles les données du LATMOS-ULB, dans la section 4.3.2,
la procédure est explicitée où on établit un profil de pression commun à tous les points du globe.
Basé sur une optimisation de la moyenne, cela conduit à des écarts importants aux niveaux des
extrema. Nous avons pu le constater pour les hautes latitudes.
Dans le but d’améliorer la confrontation, on se base maintenant sur la pression telle qu’elle
est fournie par EUMETSAT.
4.4.1 Récupération de la pression EUMETSAT
Les données du LATMOS-ULB sont réparties sur des niveaux d’altitude. La première valeur
en [ppm] correspond à la concentration en ozone entre les kilomètres 0 et 1, la seconde en 1 et
2, etc. Cependant, EUMETSAT ne fournit pas directement le profil de pression nécessaire au
calcul de la conversion (voir l’équation 3.3). On dispose alors de la température sur des niveaux
de pressions. Pour obtenir la pression en fonction de l’altitude, il faut alors procéder à plusieurs
calculs.
Tout d’abord, on récupère l’altitude Z pour les différentes températures T suivant les ni-
veaux de pression P :
R·T P
Z=− · ln
Mair · g P0
Cette équation se base sur l’équation hydrostatique 3.2 où R est la constante des gaz parfait,
Mair la masse moléculaire de l’air, g l’accélération de la pesanteur et P0 la pression à la surface,
récupérée dans les données d’EUMETSAT. L’annexe D explicite les valeurs retenues et le code
utilisé pour la lecture de ces données.
On dispose maintenant de la température pour différentes altitudes. Cependant, celles-ci
ne sont pas sur une répartition homogène kilométrique. Pour ce faire, on procède alors à une
interpolation des valeurs sur les kilomètres 0, 1, 2, ..., 40 afin d’obtenir les températures T (Z)
à ces altitudes.
Ainsi fait, on retourne l’équation précédente en :
Mair · g
P = P0 · exp − ·Z
R · T (Z)
et on obtient la pression aux altitudes désirées.
Lecture des données LATMOS-ULB
Dorénavant, il est possible d’améliorer le calcul des colonnes partielles et totales. Ici sont
sélectionnés les couples [latitude, longitude] strictement identique afin de s’assurer que la pres-
sion à ce point là sera correcte. Cela réduit considérablement les points qui serviront ensuite
pour la comparaison.
Dans la lecture, on utilise une équation différente de l’équation 3.3. La raison se trouve dans
le format des données LATMOS-ULB. En effet, la dernière valeur correspond à la concentration
entre 39 km et le TOA (Top Of Atmosphere) équivalent à une pression de 0,5 Pa. Dans le
calcul de la colonne présente à ce niveau, c’est une forte sous-estimation de la quantité d’ozone
présente. Ainsi, pour améliorer au mieux le calcul, on procède à une étape supplémentaire. Les
pressions et températures sur les niveaux d’altitudes sont calculées jusqu’à atteindre la pression
de 0,5, puis l’équation suivante est utilisée pour calculer la colonne :
51](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-51-320.jpg)
![dU [kg/m2 ] = ρg · dz
= r · ρair · dz
MO3
= rc · ρair · dz
Mair
ρ
or P = Mair RT (4.3)
air
MO3 P Mair
= rc · · dz
Mair RT
P MO3
= rc · dz
RT
d’où, sachant que rc correspond à la fraction molaire,
P MO3
dU [Dobson] = rc [ppb] · 10−9 · · f · dz (4.4)
RT
où nous disposons des profils de pression P et température T issus des données d’EUMET-
SAT. Il s’agit en fait d’affiner le calcul. En effet, utilisée sur tous les niveaux d’altitudes, cette
expression de la colonne d’ozone se sert du profil de pression ET du profil de température.
Le profil de température est donc nécessaire pour cette méthode, cependant, il n’est pas
forcément disponible. Dans ce cas, comme l’annexe D le précise, le profil de température est
imposé à une valeur fixe. Il est donc facile de sauter les points qui n’ont pas de profil de tem-
pérature. Malheureusement, sur une journée, la séléction des points de latitudes et longitudes
identiques ne va pas donner ∼18% du total des points, mais seulement ∼1%. Il y a donc ici une
importante réduction des points utilisés pour les statistiques.
4.4.2 Comparaison aux valeurs précédentes
Il est intéressant d’effectuer une comparaison aux valeurs précédentes obtenues avec le profil
de pression constant sur tout le globe. Sur la figure 4.19 est représenté le dénombrement de
l’écart relatif pour la journée du 1er septembre 2008. Sur la totalité de la surface du globe,
correspondant pour cette journée à 390 points, la moyenne de l’écart relatif est de -8,53%, avec
un pic autour de +5%. De cela il est possible de considérer que même si les nouvelles données
LATMOS-ULB sont supérieures au niveau des colonnes totales en nombre important, des gros
écarts subsistent où la colonne totale était très fortement surestimée. En regardant la courbe
rouge qui est une sélection des points situés en dessous de 60˚S, on s’aperçoit que les écarts
relatifs sont exclusivement entre -50% et -20%. Le trou d’ozone en Antarctique, sous-estimé
par la première version LATMOS-ULB, retrouve donc ses valeurs réelles. Ici, la moyenne de
l’écart relatif tombe à -34.39%, ce qui est très important.
Sur la figure 4.20, on voit l’effet d’un profil de pression différent sur les colonnes totales
d’ozone qui en seront déduites. Sur les latitudes basses et les hautes latitudes nord, la colonne
totale sera légèrement augmentée alors que pour les hautes latitudes sud, la colonne totale sera
fortement réduite.
On retrouve les valeurs dorénavant faibles d’ozone sur les colonnes totales des hautes lati-
tudes sud sur la figure 4.21. Malgré la forte réduction du nombre de points (390 contre 146161),
on distingue quelques similitudes au dessus de 60˚S. On voit se dessiner un trou au niveau de
l’Himalaya. Cela se confirme avec la figure 4.22 où 10 jours sont moyennés. La comparaison
au niveau de l’Antarctique (à droite) est flagrante.
Sur la figure 4.23 sont représentés les nuages de points correspondant aux données LATMOS-
ULB des deux méthodes avec en texte les coefficients directeurs et ordonnées à l’origine. Sur
52](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-52-320.jpg)
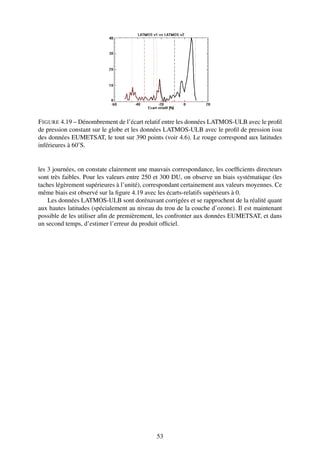
![F IGURE 4.20 – Pour deux points, observation du profil en [ppm] (courbe en haut à gauche), des
profils de pressions (suivant les calculs de la section précédente (voir l’équation 3.3) en noir,
et l’équation 4.4 utilisée maintenant en rouge. Les résultats donnent les profils d’ozone suivant
avec un écart de +9% pour le point de gauche [76.58,-91.67] et -53.46% pour le point de droite
[-86.37,-156.08], situé en dessous de 60˚S.
F IGURE 4.21 – Comparaison sur cartes des valeurs du LATMOS-ULB avec l’ancienne méthode
à gauche, et la nouvelle à droite. Outre la réduction très importante du nombre de points, on
constate que la zone Antarctique est très inférieure à la première version, et semble dorénavant
bien mieux consistante avec la réalité du trou dans la couche d’ozone.
54](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-54-320.jpg)
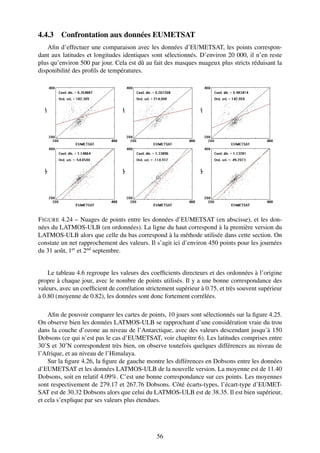
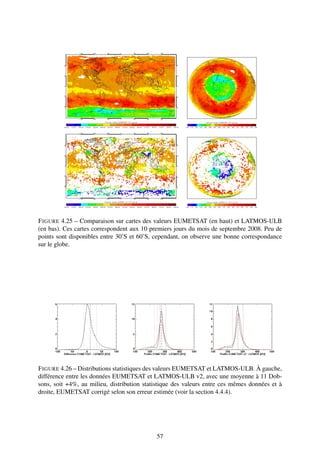
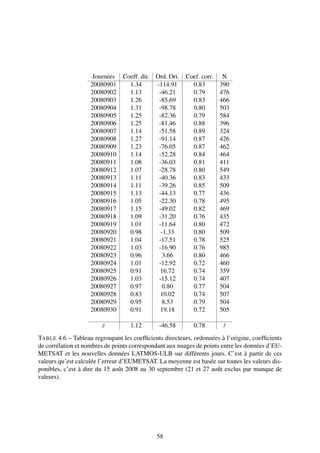

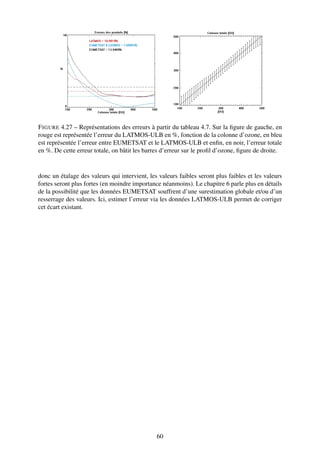
![Col. tot. [DU] Erreur [DU] Erreur [DU] Erreur [DU] Erreur [%]
LATMOS-ULB EUMETSAT Totale Totale
100 NaN* 34.21 42.38 42.38
120 25.71 31.74 40.84 34.04
140 27.05 29.27 39.85 28.47
160 28.25 26.79 38.93 24.33
180 28.22 24.32 37.25 20.70
200 26.67 21.85 34.47 17.24
220 25.77 19.37 32.24 14.66
240 22.34 16.90 28.01 11.67
260 20.68 14.43 25.22 9.70
280 22.11 11.95 25.13 8.98
300 24.92 9.48 26.66 8.89
320 25.95 7.01 26.88 8.40
340 26.71 4.53 27.09 7.97
360 27.53 2.06 27.60 7.67
380 28.33 0.41 28.33 7.45
400 29.44 2.89 29.58 7.39
420 30.37 5.36 30.84 7.34
440 31.91 7.83 32.85 7.47
460 32.85 10.31 34.43 7.48
480 37.80 12.78 39.90 8.31
500 42.64 15.25 45.28 9.08
x
¯ 21.20 14.45 27.42 11.81
TABLE 4.7 – Erreur estimée d’EUMETSAT à partir de l’erreur observée avec les données
LATMOS-ULB. La deuxième colonne correspond à l’erreur des données LATMOS-ULB, la
troisième colonne correspond à l’erreur des données EUMETSAT par rapport aux données
LATMOS-ULB, la quatrième colonne correspond à l’équation 4.5, c’est-à-dire l’erreur totale,
et la cinquième colonne correspond à l’erreur totale relative. (* : l’absence de valeur entre 95 et
105 Dobsons explique le Not a Number, qui sera assimilé à la valeur moyenne pour le calcul de
l’erreur).
61](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-61-320.jpg)
![4.5 Confrontation aux données MIPAS
4.5.1 Cas général : absence des colonnes partielles
L’instrument MIPAS est un spectromètre utilisé pour la mesure en haute résolution des
émissions spectrales gazeuses au limbe terrestre. Il surveille ainsi l’ozone dans la stratosphère.
Dans son cas, une comparaison pour l’ozone troposphérique est caduque. Comme il a été vu
dans la section 3.2.3, il existe un flag de visibilité exprimant s’il est possible d’obtenir la valeur
en concentration d’ozone. Bien souvent, l’ozone n’est pas disponible pour la première colonne
partielle et la seconde, voire la troisième. Ainsi, les colonnes totales se font sur toutes les valeurs
restantes.
À l’aide de la figure 4.28, on constate que les valeurs faibles extrèmes apparaissent surtout
lorsque les colonnes partielles [0-6] et [0-12] sont absentes. Dès qu’on ne considère que les
points où au moins sont présents les colonnes [0-12] (et donc [0-18] et total), les moyennes et
écarts types se resserrent autour des valeurs d’EUMETSAT.
F IGURE 4.28 – Au 1er septembre 2008, distribution statistique des valeurs des colonnes totales
d’ozone en rouge pour MIPAS et en noir pour EUMETSAT. En bas, sur la totalité des points,
au milieu, lorsque la colonne partielle [0-18] est présente, en haut, lorsque la colonne partielle
[0-12] est présente. Le cas où la colonne partielle [0-6] est présente n’a pas été représentée car
elle comporte moins d’une dizaine de points.
Sur la figure 4.29 sont représentées les colonnes totales en fonction de la latitude. On
constate un biais systématique (figure du haut) qui s’explique par la colonne partielle [0-6]
km majoritairement absente des données. Par exemple, pour le 1er septembre 2008, seuls 1.5%
des points disposent de valeurs entre 0 et 6 km. Sur la figure du bas, on retranche à EUMETSAT
la première colonne partielle. On constate alors un net rapprochement pour les valeurs éloignées
62](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-62-320.jpg)
![des pôles.
Dès lors qu’on considère la colonne totale, l’écart entre EUMETSAT et MIPAS est de
l’ordre de 15%. Par contre, si l’on ne sélectionne que les données de MIPAS existant sur les pre-
mières colonnes partielles ou alors qu’on ôte à EUMETSAT ses premières colonnes partielles,
la correspondance devient bonne, de l’ordre de 3.5% (pour le 1er septembre par exemple, il en
est de même pour la plupart des jours des mois d’août et septembre). On retrouve bien le fait
que l’instrument MIPAS observe aux limbes et donc sa capacité à voir les premièrs kilomètres
est très réduites.
F IGURE 4.29 – Sélection sur une longitude de la colonne totale en fonction de la latitude.
Figure du haut, les valeurs sont prises telles quelles, alors que sur la figure du bas, on ajoute aux
données MIPAS les colonnes partielles [0-6] km d’EUMETSAT correspondantes.
4.5.2 Moyenne sur août et septembre 2008
En moyennant sur les deux mois d’août et septembre, les résultats sont sensiblement simi-
laire. Le tableau 4.8 récapitule les résultats obtenus. De même, on procède à une sélection des
points qui présentent ou non des colonnes partielles. Pour la première colonne, tous les points
sont sélectionnés et l’écart est important (supérieur à 10%). Pour la seconde, ce sont les points
qui montrent au moins une colonne [0-18] km. Ici, l’écart tombe à -5.65%. De même, dans le
cas où la colonne [0-12] km est présente, l’écart tombe à -1.11%. Par contre, si l’on sélectionne
là où toutes les colonnes partielles sont présentes, on obtient -5.57%. En fait, le nombre de
point est très faible, ce qui fait que même moyennés sur 2 mois, le nombre de points n’est pas
suffisante pour une statistique valide.
Aussi, lorsque la colonne [0-18] km est présente, mais pas les colonnes inférieures, ce n’est
pas la colonne [0-18] km que l’on regarde, mais plutôt la colonne [12-18] km. [0-12] serait
alors [6-12] km toujours dans le cas où [0-6] km est absente. C’est pourquoi il n’est pas sensé
d’étudier en détails les colonnes partielles. Cela est appuyé par le nombre de points sur une
journée, représentée par la figure 4.30.
On constate, comme pour les autres jeux de données, que la colonne totale au niveau des
hautes latitudes (<-60˚) est faible. Cependant, ici, en sélectionnant les points inférieurs à -60˚,
on constate que beaucoup ont leurs premières colonnes partielles absentes, ce qui contribue à la
faiblesse des valeurs des colonnes totales (comme on a pu le voir sur la figure 4.28).
63](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-63-320.jpg)
![x¯ x
¯ x
¯ x
¯
EUMETSAT 275.72 275.72 275.72 279.36
MIPAS 245.68 260.12 272.66 263.80
∆ -10.90% -5.66% -1.11% -5.57%
TABLE 4.8 – Écarts sur les moyennes totales des colonnes totales sur les 2 mois d’août et
septembre 2008. À gauche, sélection de tous les points, ensuite, sélection où [0-18] km = 0,
sélection où [0-12] km = 0 et enfin sélection où [0-6] km = 0. Seuls les jours communs entre
EUMETSAT et MIPAS ont été sélectionnés (absence de 3 jours par mois environ). La dernière
moyenne d’EUMETSAT diffère car certains jours de MIPAS ne disposent pas de la colonne
[0-6] km.
F IGURE 4.30 – Carte de la colonne totale d’ozone (DU) issue d’une journée de données MIPAS.
Le nombre de points est pour cette journée du 1er septembre 2008 est de 2318, dont 35 disposent
d’une colonne [0-6] km, 1257 d’une colonne [0-12] km et 2108 d’une colonne [0-18]km.
64](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-64-320.jpg)
![4.6 Sortie de Niveau 3
La transformation des données en données de Niveau 3 quant à la répartition sur grille se
fait assez facilement. Le programme fait tourner 2 boucles, l’une sur les latitudes et l’autre sur
les longitudes. À chaque point de grille, on recherche quels sont les points qui satisferaient les
conditions suivantes :
i − pas/2 < latitude ≤ i + pas/2
∀(i, j) ∈ ([−90, 90], [−180, 180]),
j − pas/2 < longitude ≤ j + pas/2
C’est une manière assez basique de répartir sur une grille. Il existe en effet des grilles plus
complexes qui permettent par exemple, de réduire le nombre de mailles sur les hautes latitudes
(voir section 2.2.2). Ici, le choix s’est porté sur 2 types de grille : 1.4˚ et 2.8125˚. La plupart
des modèles climatiques se font sur une grille de 2.8125˚ mais la tendance est à l’heure actuelle
d’affiner la précision des données, en les répartissant sur une grille de 1.4˚, d’où l’utilisation
pour les comparaisons précédentes et suivantes de ce pas de grille.
Dès lors, il est possible de juger quelle est l’erreur occasionnée par ce passage à une grille.
La figure 4.31 montre pour la colonne totale les histogrammes des valeurs d’EUMETSAT du
produit L2 en comparaison avec la grille de 1.4˚ et 2.8125˚. La différence avec le produit L2
s’accroît lorsque la grille se fait avec un pas plus important. Cependant, en regardant le ta-
bleau 4.9, les variations sont faibles pour la moyenne (inférieures à 5%) et pour l’écart-type
(inférieures à 20%).
F IGURE 4.31 – Distributions statistiques des valeurs de colonnes totales d’EUMETSAT issues
des produits de niveaux 2 (en noir) en comparaison avec la répartition sur grille (en rouge). À
gauche, sur une grille de 1.4˚×1.4˚et à droite, sur une grille de 2.8125˚×2.8125˚. Les valeurs
sont en pourcentage du nombre total de points valides (ie les points où il n’y a pas de données,
-999, ont été omis).
Sur tout le mois de septembre 2008, l’écart relatif entre la moyenne de la colonne totale
d’EUMETSAT et sa version posée sur une grille de 1.4˚×1.4˚ est de 1.13%. Son maximum est
de 1.26% pour le 14 septembre. L’écart relatif étant toujours positif, on peut dire qu’établir les
données d’EUMETSAT sur une grille, ici de 1.4˚×1.4˚, surestime de façon permanente d’une
valeur de 1.13% sur le mois de septembre. En prolongeant le même raisonnement avec le mois
d’août 2008, on tombe à 1.05%. L’approximation de +1% semble valide pour la répartition sur
grille.
Quant aux colonnes partielles, sur les mois d’août et septembre 2008, les écart relatifs sont
de : 2.40% pour la colonne [0-6] km, 0.54% pour la colonne [0-12] km et 3.38% pour la colonne
65](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-65-320.jpg)
![EUMETSAT [Dobson] L2 1.4˚×1.4˚ 2.8125˚×2.8125˚
Colonne [0-6] km x
¯ 20.90 20.32 (-2.75%) 20.08 (-3.88%)
σ 5.06 5.27 (+4.11%) 5.31 (+4.94%)
Colonne [0-12] km x
¯ 35.03 34.73 (-0.85%) 34.58 (-1.28%)
σ 6.27 6.58 (+5.08%) 6.64 (+5.97%)
Colonne [0-18] km x
¯ 47.90 49.18 (+2.66%) 49.68 (+3.70%)
σ 10.45 11.12 (+6.40%) 11.28 (+8.02%)
Colonne totale x
¯ 284.44 285.89 (+0.51%) 286.66 (+0.78%)
σ 23.86 27.15 (+13.78%) 28.06 (+17.61%)
TABLE 4.9 – Sur la journée du 1er septembre 2008, valeurs des colonnes partielles et totales
d’ozone suivant la répartition ou non sur grille, de 1.4˚×1.4˚et 2.8125˚×2.8125˚.
[0-18] km. Les résultats sont tous inférieurs à 5%, c’est pourquoi dorénavant, on considère la
répartition sur grille du produit L2 d’EUMETSAT comme validée pour la comparaison avec les
sorties de modèles.
66](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-66-320.jpg)
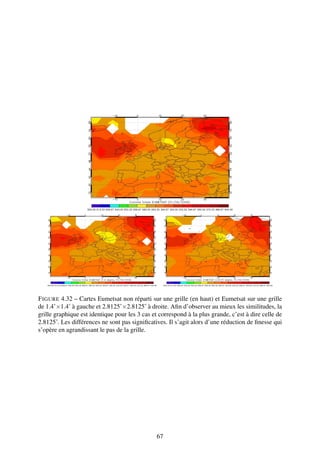

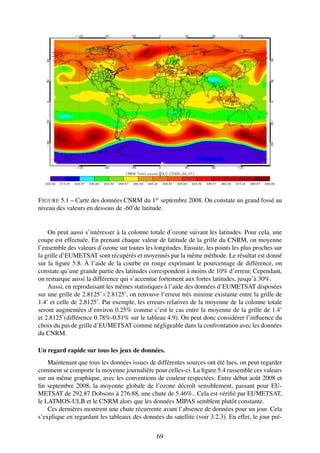
![F IGURE 5.2 – Distributions statistiques des valeurs en colonne totale d’ozone au 1er septembre
2008 pour les données d’EUMETSAT (en noir) sur grille et celles du CNRM (en vert). À gauche
est représenté la globalité des données, alors qu’à droite, une sélection des latitudes supérieures
à -60˚a été faite pour constater l’importance de la zone Antarctique dans les données du CNRM
(voir aussi 5.1).
[Dobson] EUMETSAT 1.4 CNRM
Colonne [0-6] km x
¯ 20.32/21.88 16.73 (-17.66%)/16.98 (-22.40%)
σ 5.27/3.59 1.98 (-62.36%)/2.00 (-44.28%)
Colonne [0-12] km x
¯ 34.73/36.56 36.49 (+4.95%)/35.21 (-3.68%)
σ 6.58/4.86 12.51 (+90.03%)/11.97 (+146.48%)
Colonne [0-18] km x
¯ 49.18/49.71 73.26 (+48.97%)/66.28 (+33.35%)
σ 11.12/11.60 39.22 (+252.78%)/36.56 (+215.32%)
Colonne totale x
¯ 285.89/292.41 269.97 (-5.57%)/284.71 (-2.63%)
σ 27.15/22.12 50.02 (+84.24%)/34.63 (+56.53%)
TABLE 5.1 – Sur la journée du 1er septembre 2008, valeurs des colonnes partielles et totales
d’ozone suivant la répartition ou non sur grille, de 1.4˚×1.4˚et 2.8125˚×2.8125˚. En noir, les
valeurs correspondant à la totalité du globe. En rouge, uniquement les latitudes supérieures à
-60˚.
cédant une absence est souvent moins couvert que le reste (entre 25% et 75% contre >75% le
reste du temps). La grille d’EUMETSAT montre un biais constant surestimant de 2 à 4 Dob-
sons les valeurs non-grillées que l’on a déjà observé dans la section 4.6. Il est aussi intéressant
de constater que l’écart entre les données d’EUMETSAT et celles du CNRM, de l’ordre de
5%, reste constant sur les 2 mois et la différence entre les extrèmes est identiques, le CNRM
chute lui aussi d’environ 6% entre début août et fin septembre. A contrario, les données du
LATMOS-ULB (disponibles seulement à partir du 14 août) sont légèrement supérieures à celles
d’EUMETSAT avant de décroître légèrement plus rapidement. L’écart relatif varie donc entre
+3.24% et -5.01%.
Par la suite, on s’intéresse de nouveau à la confrontation entre les données d’EUMETSAT
et du CNRM uniquement.
70](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-70-320.jpg)
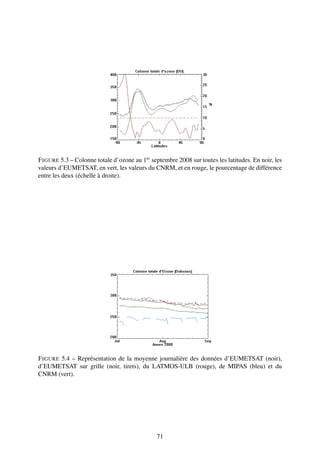
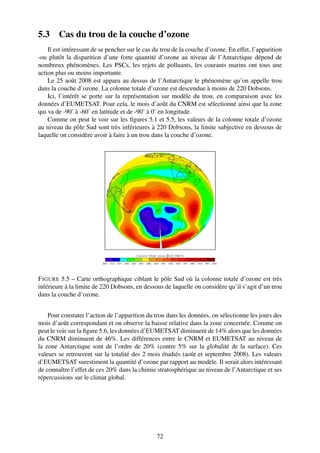
![F IGURE 5.6 – Colonne totale entre [-90˚,-60˚] en latitude et [-90˚,0˚] en longitude, ciblée sur la
zone Antarctique. Sont représentées en pointillés les moyennes avant et après le 24 août, date
d’apparition du trou de la couche d’ozone et les valeurs des chutes. EUMETSAT chute de 14%
alors que le CNRM chute de 46%.
73](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-73-320.jpg)

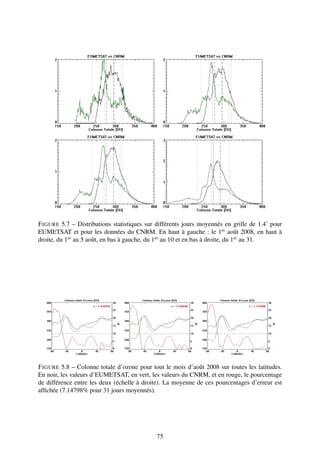
![5.5 Et sur plusieurs mois...
La plupart des comparaisons produites jusqu’ici se sont faites sur les mois d’août et sep-
tembre 2008. Or, comme le montre la figure 5.9, le déficit en ozone est surtout présent durant
les moits d’août, septembre, octobre et novembre de l’année. Il est alors intéressant de regarder
F IGURE 5.9 – Déficit en millions de tonnes de l’ozone en dessous de 40˚S, relatif à 220 DU.
On observe bien l’apparition cyclique du trou au niveau des mois d’août, septembre, octobre et
novembre de l’année. Crédit : NASA.
ce qu’il en est des autres mois de l’année. La figure 5.10 montre les distributions statistiques
à gauche des mois de janvier, février et mars de l’année 2008, et à droite, des mois d’août,
septembre et octobre de la même année. Pour les trois premiers mois d’hiver, la moyenne
d’EUMETSAT est de 294.92 DU pour 283.75 côté CNRM, soit un écart relatif de -4.75%. Les
écarts-types, quant à eux, sont respectivement de 57.79 et 53.72 DU, soit -7.05%. Il y a donc
une très bonne corrélation entre les distributions d’EUMETSAT et du CNRM sur ces mois-ci,
et même sur l’écart-type. Il est intéressant de noter qu’ici, c’est l’écart-type d’EUMETSAT qui
est supérieur à celui du CNRM et non l’inverse comme il a déjà été observé dans les résultats
précédents (voir tableau 5.1). Sur les trois mois concernés par le trou dans la couche d’ozone
(ici août, septembre et octobre), les moyennes d’EUMETSAT et du CNRM sont respective-
ment de 276.30 et 263.35 DU (-4.69%) pour des écarts-types respectifs de 30.29 et 69.50 DU
(+129.40%). Ici, la correspondance au niveau des moyennes est tout aussi bonne, cependant,
du fait de l’apparition de valeurs très faibles au niveau de l’Antarctique (valeurs inféreures
à 200 Dobsons sur la figure 5.10 de droite), l’écart-type des colonnes totales du CNRM est
bien supérieur à celui d’EUMETSAT. Lorsqu’on "corrige" les valeurs d’EUMETSAT (voir sec-
tion 4.4.4), la différence entre EUMETSAT et le CNRM diminue de manière notable : -2.67%
pour janvier/février/mars et -1.45% pour août/septembre/octobre.
Les données sur l’année montrent bien l’apparition du trou dans la couche d’ozone. Comme
la figure 5.9 le montre, le modèle du CNRM repète cette apparition du trou vers juillet/août
en accusant une diminution de sa colonne totale moyenne pour les valeurs inférieures à 40˚S
(c’est-à-dire entre -90˚et -40˚). Le minimum descend jusqu’à 50 DU en septembre et octobre
et la moyenne passe d’environ 265 DU à 210. Par contre, le maximum présente une hausse
inattendue au lors de l’apparition du trou, ce qui peut expliquer la faible baisse de la moyenne
sur ces latitudes.
La figure 5.12 permet un regard critique sur l’ensemble des 2 mois de janvier et février
2008 (pour des raisons de mémoire informatique, le mois de mars n’a pas pu être inclu sur
les graphes, cependant, les résultats associés dans le tablea 5.4 comprend les valeurs du mois
de mars). Les quatre colonnes correspondent aux colonnes partielles [0-6], [0-12], [0-18] km
76](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-76-320.jpg)
![F IGURE 5.10 – Distribution statistique sur 3 mois des données EUMETSAT et CNRM. Sur la
figure de gauche, les mois de Janvier, Février et Mars 2008, sur la figure de droite, les mois
d’Août, Septembre et Octobre 2008.
F IGURE 5.11 – Minimum, moyenne et maximum de la colonne totale issue des données CNRM
en dessous de 40˚S, sur toute l’année type.
et à la colonne totale, les quatre lignes, quant à elles, correspondent aux différentes latitudes.
La première regroupe la totalité du globe, la deuxième les latitudes entre 45˚N et 90˚N, puis
45˚S à 45˚N, et enfin 90˚S à 45˚S. À l’aide de cette figure et du tableau 5.4, plusieurs points
sont notables. Il y a un très faible écart entre EUMETSAT et le CNRM sur les colonnes totales
globales et sur les latitudes faibles (entre 45˚S et 45˚N), de l’ordre de 5%. La colonne totale
des latitudes élevées côté nord correspondent plutôt bien aussi (<10%). Les différences entre
les colonnes [0-6] km sont correctes quand on juge de l’écart absolu, de l’ordre de quelques
Dobsons, ce qui est normal sur de faibles valeurs (∼20 DU). La colonne [0-18] km quant à elle
montre d’importants écarts, sauf en ce qui concerne les latitudes faibles.
En comparaison, le tableau 5.4 regroupe ces mêmes calculs mais pour les mois d’août, sep-
tembre et octobre 2008. Les résultats sont très similaires au niveau de la colonne totale (comme
l’écart plus important au niveau des hautes latitudes sud). On retrouve le faible écart de la co-
lonne [0-18] km aux faibles latitudes. Sur ces 3 mois, la correspondance pour la colonne [0-12]
km est moins importante qu’elle ne l’est pour les mois de janvier, février et mars. Enfin, au
77](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-77-320.jpg)
![Janvier, février et mars 2008
0-6 km 0-12 km 0-18 km Col. tot.
Global EUMETSAT 19.40 35.52 48.32 298.16
CNRM 16.27 31.10 70.96 284.04
∆¯ [%]
x -16.14 -4.38 49.84 -4.74
45˚N - 90˚N EUMETSAT 15.80 32.11 70.78 386.46
CNRM 16.28 35.78 127.51 358.15
∆¯ [%]
x 3.02 11.40 80.16 -7.32
45˚S - 45˚N EUMETSAT 21.36 33.34 40.44 269.26
CNRM 16.05 28.20 39.65 255.67
∆¯ [%]
x -24.84 -15.40 -1.96 -5.05
90˚S - 45˚S EUMETSAT 14.95 29.57 53.06 307.55
CNRM 16.72 32.22 77.05 266.67
∆¯ [%]
x 11.79 8.96 45.22 -13.29
Août, septembre et octobre 2008
0-6 km 0-12 km 0-18 km Col. tot.
Global EUMETSAT 21.09 34.81 46.63 280.39
CNRM 16.92 35.78 69.63 266.54
∆¯ [%]
x -19.80 2.80 49.32 -4.94
45˚N - 90˚N EUMETSAT 19.67 36.82 59.68 301.19
CNRM 18.57 49.12 106.22 301.87
∆¯ [%]
x -5.60 33.40 80.00 0.23
45˚S - 45˚N EUMETSAT 22.68 35.51 42.81 279.47
CNRM 16.48 28.73 41.29 270.25
∆¯ [%]
x -27.37 -19.08 -3.56 -3.30
90˚S - 45˚S EUMETSAT 14.37 27.29 46.01 262.69
CNRM 15.93 36.55 89.72 223.78
∆¯ [%]
x 10.93 33.93 95.01 -14.81
TABLE 5.4 – En unité Dobson, tableau regroupant les valeurs des moyennes d’EUMETSAT et
du CNRM sur différentes latitudes et pour les colonnes partielles/totale, sur les mois de janvier,
février et mars 2008, puis d’août, septembre et octobre de la même année. La première partie
correspond à la figure 5.12.
niveau des hautes latitudes sud, là où le trou de la couche d’ozone apparaît, les écarts sont
importants et ne descendent pas en dessous de 10%.
78](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-78-320.jpg)
![La figure 5.13 complète la 5.11 avec les données EUMETSAT (en noir) et EUMETSAT
dans sa version corrigée (en rouge). Sont représentés les minima, moyennes et maxima sur
les mois disponibles des données inférieures à 40˚S (suite à un problème informatique, les
données des mois d’avril, mai, juin, juillet et novembre de l’année 2008 sont temporairement
indisponibles). On constate plusieurs caractéristiques. Les minima correspondent bien sur la
période hiver (janvier, février et mars), alors que la moyenne est supérieure côté EUMETSAT.
Ce même décalage se retrouve sur la moyenne pour les mois d’août, septembre et octobre et les
minima du CNRM sont assez inférieurs aux données d’EUMETSAT. Côté maxima, on observe
une bonne correspondance pour les mois d’août, septembre et octobre, mais sur les mois d’hiver,
il y a un écart très important avec les données d’EUMETSAT pouvant dépasser les 500 DU,
toujours sur la zone de latitudes inférieures à 40˚S.
F IGURE 5.13 – Minimum, moyenne et maximum de la colonne totale issue des données CNRM
en vert, EUMETSAT en noir, et EUMETSAT corrigé en rouge, le tout en dessous de 40˚S, sur
toute l’année type et 2008.
La comparaison sur plusieurs mois à permis d’apporter de bons résultats sur les mois de
janvier, février et mars. En effet, les colonnes totales de ces mois sont correspondent assez bien
sur la globalité de la surface, légèrement moins sur les hautes latitudes sud. Aussi, les colonnes
[0-18] km sont similaires entre 45˚S et 45˚N. La colonne [0-12] km montre un comportement
différent s’il s’agit des mois de janvier/février/mars ou des mois de août/septembre/octobre. Les
écarts sont plus importants sur ces derniers mois.
80](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-80-320.jpg)
![5.6 Extrema
On isole dans cette section un cas extremum afin de mettre en évidence le problème d’une
faible teneur en ozone sur les hautes latitudes. Le jour sélectionné est le 30 septembre. La
figure 5.14 de gauche montre les teneurs en ozone de la colonne totale. Ici, l’échelle n’est
plus bornée en valeur inférieure à 200 Dobsons, mais au minimum des valeurs : 61 Dobsons.
À droite, l’histogramme des valeurs (en comparaison avec EUMETSAT pour le 30 septembre
2008) montre clairement une quantité non négligeable de valeurs entre 60 et 200 Dobsons alors
qu’EUMETSAT présente une part de valeurs faibles, mais comprises entre 180 et 220 Dobsons.
F IGURE 5.14 – Carte du CNRM en représentation orthographique ciblée sur la zone Antarctique
afin de mettre en évidence le trou de la couche d’ozone et ses valeurs extrêmement faible. Ici,
l’échelle a été adaptée aux valeurs où 400 Dobsons reste le maximum, mais le minimum devient
60 Dobsons. À droite, distribution statistique des valeurs EUMETSAT et CNRM, à partir de 0
Dobson.
Cependant, lorsqu’on regarde sur la totalité des valeurs, figure 5.15, la moyenne est de
281.65 Dobsons pour EUMETSAT contre 258.98 Dobsons pour CNRM, ce qui conduit à un
écart relatif de -8% (inférieure à 10%). La carte paraît à dominante rouge du fait de l’étalement
choisi des valeurs. En assignant la valeur minimale limite à 200 Dobsons, on réobtiendrait un
étalement plus naturel, mais on perderait l’information sur les hautes latitudes autour du pôle
Sud. Dès lors qu’on s’intéresse aux différences entre EUMETSAT et CNRM, figure 5.16, on
remarque simplement avec l’échelle que les écarts sont grands. Cela se vérifie avec l’écart relatif
des écarts-types : +91% (voir 5.14 à droite). Même si l’absence de données d’EUMETSAT
autour de l’Antarctique ne permet pas de visionner correctement l’importance de l’écart, il est
assez facile de le prédire.
De même, sur la même journée, il est intéressant de regarder les colonnes partielles. Les
informations sont regroupées dans le tableau 5.5.
EUMETSAT CNRM
x
¯ σ x
¯ σ
Col [0-6] km 20.79 4.43 17.01 (-18.18%) 2.10 (-52.67%)
Col [0-12] km 34.54 5.68 35.43 (+2.60%) 10.63 (+87.09%)
Col [0-18] km 46.53 10.93 64.80 (+39.25%) 35.75 (+226.99%)
Colonne totale 281.65 37.60 258.98 (-8.05%) 71.85 (+91.09%)
TABLE 5.5 – Sur la journée du 30 septembre 2008, tableau des moyennes et écarts-types des
différentes colonnes pour EUMETSAT et le CNRM (en Dobsons).
81](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-81-320.jpg)
![F IGURE 5.15 – Carte des valeurs du CNRM, comprises entre 60 et 400 Dobsons (échelle étirée
par rapport aux précédentes cartes), pour la colonne totale, un 30 septembre.
Seules les moyennes de la colonne partielle [0-12] km et de la colonne totale correspondent
assez bien. La colonne [0-18] km montre un écart très mauvais alors que pour la colonne [0-6]
km, même si l’écart relatif est important, l’écart absolu est inférieur à 4 Dobsons. Les écarts-
types, quant à eux, présentent des variations très importantes. Il faut bien garder en tête que la
distribution des valeurs du CNRM ne suit pas une distribution statistique de type Gaussienne.
5.7 Autre sortie de modèle : LMDZ-REPRO
Le LATMOS-ULB n’a malheureusement pas pu nous fournir les champs du modèle clima-
tique LMDZ-REPRO (pour Laboratoire de Météorologie Dynamique Zoom - REPROBUS) qui
sera utilisé pour le CMIP5. Ce travail sera cependant intégré durant le mois de septembre dans
le cadre du CCI, et les résultats seront inclus dans le rapport entreprise pour le CNES.
82](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-82-320.jpg)

![Chapitre 6
Regard critique sur les données
EUMETSAT
Après avoir effectué une comparaison détaillée des données d’EUMETSAT, produit officiel,
avec les données satellitaires LATMOS-ULB, MIPAS et le modèle CNRM, il est intéressant de
regarder dans l’ensemble de la littérature ce à quoi on peut s’attendre. Fruit d’une collabora-
tion entre le KNMI (Koninklijk Nederlands Meteorologisch Instituut) et le FMI (Ilmatieteen
laitos ou Finnish Meteorological Institute), l’instrument OMI (Ozone Monitoring Instrument) à
bord du satellite Aura fournit pour la NASA des données d’ozone journalières en utilisant des
spectres de rayonnement UV et visible. Les données sont publiques et accessibles sur le site
http://ozonewatch.gsfc.nasa.gov/.
Cette première comparaison rapide entre un instrument observant dans l’UV & visible ([33])
et un instrument observant dans l’IR est intéressante. Elle permet de voir les écarts de valeurs
entre des données issues des deux domaines de spectroscopie. En effet, la spectroscopie UV
& visible s’intéresse aux transitions électroniques alors que la spectroscopie IR s’intéresse aux
transitions vibrationnelles (plus de détails section 6.2).
À partir de la figure 6.1, deux points importants sont à retenir. Le premier correspond à
la décroissance des valeurs au niveau du trou de la couche d’ozone en Antarctique. En effet,
l’ozone des colonnes totales situées en dessous de 40˚S décroit de manière continue entre 220 et
120 selon OMI, alors que les données EUMETSAT chutent de 300 à 250. C’est là qu’intervient
le second point : si l’on sélectionne les données inférieures à 60˚S pour EUMETSAT, la chute
est plus importante (jusqu’à 200 DU). Cette distinction entre les latitudes inférieures à 60˚S et
40˚S montre que pour les données EUMETSAT, le trou est de taille plus petite que pour les
données OMI. Dans les deux cas, les valeurs d’EUMETSAT sont bien trop supérieures aux
données OMI.
6.1 Surestimation globale
Après avoir comparé les données EUMETSAT aux autres jeux de données (LATMOS-ULB,
LATMOS-ULB v2.0 et MIPAS), ainsi qu’à la sortie du modèle CNRM-CCM, les différents
résultats ont placé les valeurs d’EUMETSAT au-dessus des autres (voir figures 4.7, 4.8, 4.10,
4.12, 4.25, 4.28, 5.2, 5.4, 5.6, et 6.1).
Sur toutes ces figures, les colonnes partielles et la colonne totale d’EUMETSAT présentent
des moyennes dans l’expectative, cependant, il est légitime de se demander d’où vient cette
surestimation observée. Il peut s’agir d’un biais systématique issu de la mesure.
Les écarts-types sont quant à eux très inférieurs à la plupart des autres jeux de données. En
effet, sur la colonne totale, les écarts-types des données LATMOS-ULB, MIPAS ou CNRM sont
d’environ supérieures de 10 DU aux données EUMETSAT. Celles-ci sont donc plus resserrées
84](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-84-320.jpg)

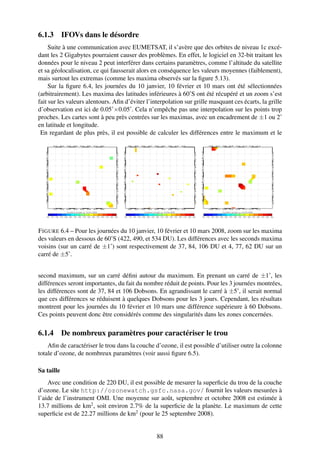

![F IGURE 6.5 – Aire, minimum et déficit en masse de l’ozone au dessus de l’Antarctique à partir
des données OMI de la NASA, avec un trio moyenne/maximum/minimum tiré de l’ensemble
des données 1979-2010, l’année 2010 en bleu et l’année 2011 en rouge. Crédit : [33].
90](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-90-320.jpg)
![6.2 InfraRouge contre Ultra-Violet
6.2.1 Infrarouge
La spectroscopie infrarouge est un outil puissant pour identifier de nombreux composés chi-
miques du fait que la plupart possèdent un spectre rovibrationnel propre. L’utilisation a fortiori
d’un interféromètre de Michelson permet une sensibilité élevée, même pour les mélanges ga-
zeux complexes, une meilleure sélection et une grande rapidité d’acquisition ([34]). Il s’agit là
de l’IRTF : spectroscopie Infrarouge à Transformée de Fourier.
Dans le domaine infrarouge, 3 bandes (3, 5 et 10 µm) sont utilisées à la télédétection de
l’ozone. Comme la figure 6.6 à gauche le montre, la zone de 10 µm, 1100 cm-1 est la plus
intense et de surcroît celle utilisée pour la spectroscopie à transformée de Fourier (cas IASI).
Du fait de la répartion de l’ozone dans l’atmosphère, à environ 10% dans la troposphère
et 90% dans la stratosphère, il est nécessaire de connaître les sections efficaces IR à 1% pour
connaître la concentration de l’ozone avec une précision de 10% dans le cas d’observation au
nadir.
En effet, l’absorption est reliée à la section efficace d’après la loi de Beer-Lamber
A(λ) = σ(λ) · l · C
où A(λ) est l’absorbance (sans unité), σ(λ) la section efficace d’absorption (en cm2 /molécule),
l la longueur du milieu (en cm) et C, la concentration en molécule/cm3 . Différentes études pour
mesurer avec précision cette section efficace dans le domaine infrarouge à 10 µm sont en bon
accord, à 2% près, cependant, l’une des dernières études montre un désaccord de 4.4% ([35]).
6.2.2 Ultra-violet
Côté utra-violet, le spectre s’étend sur une gamme spectrale allant de 240 à 800 nm, séparés
en 4 bandes différentes : Hartley, Huggins, Chappuis et Wulf (voir figure 6.6, à droite). L’ab-
sorption se fait plus forte dans la bande de Hartley (entre 200 et 300 nm) avec un maximum à
254 nm.
La spectroscopie la plus répandue est ici la spectroscopie d’absorption optique différentielle
(DOAS) au nadir. Elle s’opère pour la télédétection essentiellement sur les bandes de Huggins
et Hartley. Les spectromètres embarqués à bord de satellites permettent la détection de l’ozone
troposphérique et les colonnes verticales peuvent être extraites des mesures aux niveaux des
fortes absorptions.
Quant aux sections efficaces UV de l’ozone, de nombreuses études ont fourni des valeurs
dont les désaccords atteignent jusqu’à 10%. Les écarts tombent à 1-2% pour la région spec-
trale inférieure à 350 nm. La génération de l’ozone peut être opérée dans différentes conditions
expérimentales pouvant conduire à ces écarts.
6.2.3 Intercomparaison et correction ?
Les satellite ENVISAT et EOS AURA (Earth Observing System) ont permis des mesures
simultanées dans la région spectrale UV-visible et l’IR à l’aide de leurs instruments embarqués,
respectivement SCIAMACHY, GOMOS, et OMI, TES. Des désaccords entre les mesures ont
été mis en évidence, de l’ordre de 5% entre les mesures par IRTF de l’ozone et les mesures par
sonde UV ([36] & [37]).
De nouvelles études combinent les données des deux régions spectrales, en utilisant des
instruments à bord du même satellite, comme le couple OMI et TES, et le couple GOME-2
et IASI, utilisant l’UV entre 290 et 320 nm, et l’IR autour de 10 µm. Cependant, l’étude du
91](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-91-320.jpg)
![F IGURE 6.6 – Bandes spectrales IR et UV de l’ozone, avec le pic IR à 1100 cm-1 et les bandes
de Hartley et Huggins pour l’UV. Crédit : [34].
Rutherford Appleton Laboratory (RAL) montre que la combinaison des deux régions spectrales
n’est possible que dans la connaissance cohérente et précise des sections efficaces IR et UV de
l’ozone à moins de 1% près ([38]).
Récemment, une étude faite sur une large gamme infrarouge et sur plusieurs longueurs
d’onde dans l’UV ([39]) montre une différence systématique de 5.5% avec la base de don-
nées officielle HITRAN (high-resolution transmission molecular absorption database). Ainsi,
de nouvelles mesures spectroscopiques en laboratoire se doivent d’estimer avec haute précision
les sections efficaces dans l’infrarouge et l’ultraviolet pour permettre a posteriori la mise en
place de mesure IR à l’aide de sondeurs UV et enfin, accéder à des mesures atmosphériques de
l’ozone présentant une très bonne corrélation.
92](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-92-320.jpg)
![6.3 Possibles origines des écarts
Plusieurs hypothèses sont émises ici quant aux valeurs faibles sur la colonne totale fournies
par EUMETSAT, en particulier sur les hautes latitudes. Aucune démonstration n’est donnée,
mais des études plus complètes pourraient vérifier -ou non- ces hypothèses.
6.3.1 Les réseaux de neurones
Les réseaux de neurones sont utilisés par EUMETSAT pour inverser les spectres en radiance
afin d’obtenir les valeurs des colonnes partielles et totales. Comparé à la méthode d’estimation
optimale (OEM), les réseaux de neurones sont très rapides et permettent un rendu de données
dans la journée.
En bref, un neurone est une fonction de transfert élémentaire qui calcule une sortie sj en
fonction d’un ensemble d’entrées si , i = 1, ..., m tel que :
m
j
sj = f w i si + β j
i=1
j
où f représente la fonction de transition du neurone, wi le poids du neurone si et β j le biais
appliqué au neurone. Le réseau de neurones est alors un ensemble de neurones inter-connectés
où chaque neurone reçoit et envoie de l’information aux neurones avec lesquels il est connecté
(description plus complète sur [40]). Il s’agit donc au préalable de calibrer le réseau de neurone
afin de déterminer les paramètres de pondération et de biais. L’information d’un a priori est
donc nécessaire pour arriver à la solution.
C’est au niveau de la connaissance de l’a priori que peut se trouver l’origine des écarts. En
effet, un a priori se base sur le cas général, une moyenne estimée et ainsi, les valeurs extrèmes
des colonnes partielles ou totales subiront un "adoucissement" de leur caractère "extrème". Les
valeurs les plus faibles seront plus fortes et les valeurs les plus fortes seront plus faibles.
6.3.2 La température de surface
La spectroscopie IR utilise la radiance exprimée avec l’équation 3.4 où est utilisée la tem-
pérature. La figure 6.7 ([41]) montre les spectres en radiance au-dessus de l’Antarctique (donc
à faible température de surface). En bleu, au-dessus de l’océan, et en rouge, au-dessus du conti-
nent. Un bon spectre en radiance nécessite un fort contraste thermique, et des températures
faibles comme c’est le cas en Antarctique conduiront alors à un signal faible, voir à une ab-
sence de signal. À 1100 cm-1 , raie de l’ozone, le signal est sur cette figure très faible, voire
inexistant. Cela peut conduire a posteriori à de fortes erreurs dans l’inversion, et donc dans le
résultat de la colonne totale.
On observe sur la figure 6.8 l’ozone au niveau de l’Antarctique. La première colonne cor-
respond à la colonne totale de l’ozone sur 4 jours consécutifs (23, 24, 25 et 26 août 2008),
la deuxième colonne correspond aux valeurs d’EUMETSAT, mais corrigées à l’aide des don-
nées LATMOS-ULB, et enfin, la troisième colonne correspond à la température de surface sur
ces mêmes points. La version corrigée d’EUMETSAT permet d’améliorer le contraste en di-
minuant les valeurs faibles. Il est facilement observable que les valeurs très faibles de l’ozone
sont dispersées sur les côtes de l’Antarctique et non au centre des terres. Lorsque l’on compare
les cartes d’ozone avec les cartes de température de surface, on constate que là où se situent
les zones les plus froides, c’est-à-dire sur terre, les valeurs d’ozone ne seront pas aussi faibles
que sur mer. Il y a donc une corrélation observée (mais non démontrée) entre la température de
surface faible et la surestimation de l’ozone au niveau de l’Antarctique.
93](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-93-320.jpg)
![F IGURE 6.7 – Spectres en radiance au-dessus de l’Antarctique. En bleu, au-dessus de l’océan,
proche de l’Antarctique, en rouge, au-dessus du continent. Crédit : [41].
6.3.3 Flag nuageux sur les pôles
Sur la figure 6.9 sont regroupés 3 cartes centrées sur l’Antarctique. La première correspond
aux données d’EUMETSAT, la deuxième aux données du LATMOS-ULB et la dernière aux
données de LATMOS-ULB calculées selon la section 4.4. Il est clair que le masque nuageux
d’EUMETSAT est plus strict que celui du LATMOS-ULB. La carte des données LATMOS-
ULB2.0 a été ajoutée dans le but d’observer que les valeurs au niveau de l’Antarctique de la
première version sont largement surestimées. Dans la nouvelle version, les points disponibles
ont des valeurs inférieures à 220 Dobsons alors que la première ne descend pas au dessous
de ces 220 Dobsons (et donc, par considération, ne valide pas la présence d’un trou dans la
couche d’ozone, voir aussi la section 4.4.2). Du fait que le flag nuageux est plus strict pour
EUMETSAT, la qualité des données est meilleure. En effet, l’absorption est différente selon le
cas et des valeurs peuvent être faussées pour ces pixels. Cependant, des algorithmes existent
pour l’extraction des concentrations en ozone au-dessus des nuages. Au niveau des pôles, les
faibles températures au sol conduiront à un faible signal, comme il a été déjà été explicité dans la
section précédente, et obtenir des valeurs en ozone au-dessus des nuages serait alors une manière
détournée de récupérer des données correctes avec cependant des erreurs non négligeables.
94](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-94-320.jpg)

![Conclusion
Dans la première partie de ce stage, je me suis plongé dans les différents modèles clima-
tiques afin d’en extraire les principales caractéristiques. Je les ai compilées dans le rapport
entreprise pour le CNES. Cela m’a permis d’estimer l’importance des mesures atmosphériques
pour les prévisions à long terme.
Afin de documenter au mieux le rendu de mon travail, j’ai écrit une fiche IASI qui servira
aux utilisateurs de données climatiques dans le cadre d’une unification des formats des diffé-
rentes ECVs.
Dans la partie consacrée aux données d’EUMETSAT, j’ai tout d’abord effectué un échan-
tillonnage, qui permettra pour le travail CCI de réduire les données fournies et par la même
occasion le temps de calcul associé.
Ensuite, dans la comparaison entre EUMETSAT et LATMOS-ULB, j’ai fait face à un pro-
blème qui s’est avéré provenir de l’écriture des données LATMOS-ULB que ce dernier a corrigé
par la suite, puis je me suis heurté au problème de conversion. J’ai décidé alors de la méthode
qui me semble la mieux appropriée pour effectuer la comparaison. Celle-ci s’avère être bonne,
et ce, malgré les écarts existants pour la colonne [0-18] km ou sur les hautes latitudes. Cette
méthode n’est malheureusement pas suffisante pour quantifier l’erreur sur EUMETSAT.
Afin de résoudre ce problème, j’utilise les profils de pression et température issus des don-
nées d’EUMETSAT pour permettre une meilleure estimation des données du LATMOS-ULB.
Malgré la réduction très importante du nombre de points disponibles pour la comparaison, j’ob-
tiens de biens meilleurs résultats et je permets une estimation de l’erreur d’EUMETSAT qui
dépend de la quantité en ozone.
J’ai ensuite étendu la comparaison avec les données MIPAS, qui souffrent de l’absence
des premières colonnes partielles et du faible nombre de points disponibles par jour, mais qui
correspondent très bien en ajoutant l’ozone troposphérique d’EUMETSAT.
Dans le but de comparer les données d’EUMETSAT aux sorties du CNRM, j’ai établi les
grilles, bases de la comparaison, puis vérifié que les données ne soient pas faussées par cette
répartition.
Enfin, j’ai effectué la confrontation des mesures satellitaires à la sortie de modèle du CNRM
où je mets en évidence d’importants écarts dans les hautes latitudes et la colonne partielle [0-18]
km, mais une bonne correspondance dans la globalité avec un écart relatif inférieur à 10%. Il
en est de même lorsqu’on moyenne les grilles sur le mois, puis sur une période plus longue, de
3 mois.
Pour conclure, j’émets un regard critique sur les données d’EUMETSAT, produit officiel
des données Ozone de IASI. Elles semblent en effet sous-estimer de façon assez importante
les colonnes totales au niveaux des hautes latitudes. Quelques raisons possibles à cet écart sont
évoquées et une rapide confrontation à des données UV, effectuée.
Il faut savoir que ce stage s’est déroulé avec de nombreux problèmes informatiques. Les
données IASI sont très volumineuses, et la place m’a souvent fait défaut. Je remercie d’avance
l’équipe DCT/SI/IM pour m’avoir prêté tour à tour leurs disques durs externes pour le stockage
des données. J’ai dû aussi m’initier à de nombreux logiciels : IDL, Scilab, ENVI et CDO,
complétant ainsi mon bagage informatique.
97](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-97-320.jpg)





![Annexe C
Fiche IASI du produit Ozone
C.1 Intent of This Document
1a) This document is intended for users who wish to compare satellite derived observations
with climate model output in the context of the CMIP5/IPCC historical experiments. Users are
not expected to be experts in satellite derived Earth system observational data. This document
summurizes essential information needed for comparing this dataset to climate model output.
References are provided at the end of this document to additional information for the expert
user.
This IASI dataset is provided as part of an experimental activity to increase the usability of
EUMETSAT satellite observational data for the model and model analysis communities. This
is not a standard MetOp satellite instrument product. It may have been reprocessed, reformated,
or created solely for comparisons with the CMIP5 model. Community feedback to improve and
validate the dataset for modeling usage is appreciated.
Dataset File Name (as it appears from EUMETSAT) :
iasi_yyyymmdd_hhmmss_metopa_nnnnn_eps_o_ozo.l2_bufr
where yyyymmdd stands for the UTC year, month, day of the data start sensing time, hhmmss
stands for the UTC hour, minute, second of the data start sensing time, nnnnn is the orbit num-
ber and ’ozo’, as product code, stands for atmospheric ozone.
Dataset File Name (as it appears from ULB) :
IASI_LATMOS-ULB_ULB_O3_yyyymmdd.tar then IASI_O3_AK_yyyymmdd_*.txt
1b) Technical point of contact for this dataset :
C.2 Data Field
CF variable name, units : [must match a variable output descriptor in the Taylor, et. al.
document that defines the CMIP5 experiment outputs] Spatial [both horizontal and vertical, if
applicable] resolution : Temporal resolution and extent : (e.g, monthly averaged, from mm/yyyy
to mm/yyyy) Coverage : (e.g, if not global, then Lat/Lon boundaries, or other appropriate limits)
Horizontal grid The IASI instrument observes the Earth up to a 12 km diameter footprint on
the ground at nadir. To do so, the full swath width of ∼2200 km (2×1100 km) is provided by
observations up to an angle of 48.3˚on both sides of the trace. 2×15 mirror positions correspond
to instantaneous field-of-views of 3.3˚×3.3˚ (50 km × 50 km at nadir).
103](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-103-320.jpg)
![Band Range [cm-1 ] Information
1 50 - 770 Temperature sounding (CO2 band)
645 - 1210 cm-1 770 - 980 Properties of surfaces and clouds
1000 - 1070 O3 sounding
1080 - 1150 Properties of surfaces and clouds
2 1210 - 1650 Water vapour sounding, N2 O, CH4 and SO2
1210 - 2000 cm-1
3 2100 - 2150 Vertical profile of the CO
2000 - 2760 cm-1 2150 - 2250 Temperature sounding, vertical profile of N2 O
2350 - 2420 Temperature sounding
2420 - 2700 Properties of surfaces and clouds
2700 - 2760 Vertical profile of the CH4
TABLE C.1 – IASI spectral band and possible information available.
Vertical grid As we need parameters to retrieve the ozone profile (see in section C.3 the pa-
ragraph about the ozone retrieval), the thermal contrast, or temperature difference ∆T is very
important for all products from infrared missions. It is significantly dependant on the geogra-
phical location, seasonal and diurnal variability, but also on the wavelength. The radiometric
accuracy in noise-equivalent radiance temperature at 280 K is 0.20 K at 650 cm-1 and 0.47 K at
2400 cm-1 (more information on [3]). Then, with the ozone retrivial, it’s possible to reach a ver-
tical resolution of a few kilometers in the UT/LS and middle atmosphere, and the tropospherics
columns. For climate change models, a vertical resolution of ∼1 km is aspired.
Spectral range The IASI instrument cover a wide spectral range, from the Thermal InfraRed
(TIR) limit at 3.62 µm (or 2760 cm-1 ) where the backscattered solar light starts to contribute, up
to 15.5 µm (or 645 cm-1 ). It covers the TIR peak and particularly the CO2 band. The instrument
is observing in 3 special bands
Coverage Global.
C.3 Data Origin
There is a full description of the IASI Level 1 (L1) products overview on [46] and [48].
Briefly, the spectra have been radiometrically calibrated during on-board (L0) processing. In
Level 1a, the ISRFEM chain is used and corrected Planck functions are applied to the spectra.
Contributions from the reflected radiance, impact of the scanning mirror at different angles (as
well as its temperature dependency) are taken into account and geolocation of IASI is estimated.
Then, in Level 1b, spectra are over-sampled by a factor of 5 and they are interpolated on a
new equidistant spectral grid by using a cubic spline interpolation.
Next, the Level 1c apply an apodisation function estimated within the ISRFEM chain and
the process finishes with the generation of the radiance cluster analysis.
Now, the step for reaching the Level 2 (L2) goes through a pre-processing phase where
the geolocation is extracted from L1c data for individual IASI IFOVs (Instantaneous Field of
Views). It uses data from ATOVS (Advanced TIROS Operational Vertical Sounder) instrument
suite, AVHRR and forecast data from numerical weather prediction to validate the L1c input
data and bring correlation mask, and cloud masks ([47]).
The objectives of the IASI L2 ground processing is the derivation of geophysical parameters
from the radiance measurements. They are : temperature profiles, humidity profiles, columnar
104](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-104-320.jpg)
![Specie Vertical Res. (DOFS) Error(%) Comment References
Medium-lived species (lifetime a few weeks to a few years)
O3 3-4 30% (0-6 km) Strong absorber Eremenko et al., 2008
2% Tot. col. with large Boynard et al., 2009
stratospheric Keim et al., 2009
contribution Massart et al., 2009
Amato et al., 2009
TABLE C.2 – Level-2 quality of ozone from IASI
ozone amounts in thick layers, surface temperature, surface emissivity, fractional cloud cover,
cloud top temperature, cloud top pressure, cloud phase, total column N2 O, total column CO,
total column CH4 , total column CO2 , error covariance, processing and quality flags.
Profile retrieval of ozone In case of L2 data, the atmospheric radiative transfer equation has
to be inverted in order to obtain the vertical ozone profile. There are two principal numerical
methods (fully explained in [45]).
The first method is based on numerical optimisations. It aims to minimise the root mean
squared difference between calculated and measured spectra at each iteration, using prediction
of the atmospheric profile and calculating the full radiative transfer. This method takes a long
time to process and does not allow performing the inversion of IASI spectra in real time (120
spectra in 8s) for the operational retrieval.
Then, the second approach uses a neural network composed of various spectra of atmos-
pheric profiles, representative of the most common atmospheric conditions. It calculates with
nonlinear interpolation the inversion of a given spectrum, faster than the first method, but ex-
treme cases of atmospheric conditions may lead to wrong columnar amounts.
Data sets of IASI L2 products are provided by EUMETSat using the neural network ap-
proach. Three research groups (LATMOS-ULB, LISA and LPMAA) also provide IASI products
as profile or partial columns.
C.4 Validation
The ozone validation is strongly dependant on the retrieval method. Here are shown data
validation with the use of EumetCast L2 products. The table C.2 indicates the characteristics of
the ozone product from a IASI mission (this is an extract of the reference [3] giving the same
data about all the IASI products) :
IASI data have been compared with Global Ozone Monitoring Experiment-2 (GOME-2),
ground-based measurements from the Dobson and Brewer network ([44]) and balloon sonde
measurements ([43]). Lower tropospheric (0-6 km) ozone partial columns are in agreement
with ozone sonde measurements (mean bias 3%, RMS about 10%) even in the case of tempe-
rature conditions less favourable for ozone retrieval. For the total ozone columns, correlation
coefficients of about 0.9 and 0.85 have been showed with GOME-2 and ground-based data res-
pectively (for an average positive bias of about 9 DU (3.3%)). The sensitivity becomes weak to
surface and planetary boundary layer ozone concentrations due to the instrument caracteristics
but gets better to free tropospheric ozone ([43]).
Tropospheric columns have been also compared with several stations around the globe and
correlation coefficients of 0.95 and 0.77 for the [surface-6 km] and [surface-12 km] partial
columns respectively have been emphasized, with positive average biases observed around 0.15
DU (1.2%) and 3 DU (11%) respectively ([44]).
105](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-105-320.jpg)
![C.5 Considerations for Model-Observation Comparisons
Because this data product is observational data, there are several aspects that distinguish this
product from model outputs. The user of this data product should be aware of them in order to
make judicious model-observation comparisons.
Cloud Influence A cloud present in the optical path can affect the radiance signal recorded
by the instrument depending on the type (water or ice cloud) and the optical thickness of the
cloud. The cloud detection is performed in order to create masks and decide which pixels are
contamined or not. It combines the information of the IASI L1c spectra with AMSU-A (Ad-
vanced Microwave Sounding Unit) data and applies 5 tests to validate the presence of clouds. If
they are detected in the field of view, the CO2 -slicing method is used to estimage the fractional
cloud cover and the cloud top pressure for the IASI IFOVs (the result depends on cloud, sur-
face signals and the instrument noise). Then, depending on the cloud amount (clear, cloudy or
cloud-clearing), the retrieval will select one type of process and may create, in the cloudy case,
profiles derived only above the cloud top.
Asynoptic Time Sampling Because MetOp satellize with a sun-synchronous polar orbit, it
samples at two fixed local solar times (09 :30 local time in the morning and 21 :30 in the
evening) so cannot resolve the diurnal cycle.
Inhomogeneous Sampling Because of the convergence of longitude lines near the poles, the
time range of data collection broadens as one moves from the equator toward either pole, with
the ranges in the polar regions including all times of day and night.
Spectral resolution IASI is based on a Michelson-type Fourier-transform spectrometer with a
maximal optical path difference of 2 cm and a spectral range from 645 cm-1 to 2760 cm-1 . After
apodisation with a Gaussian function, a spectral resolution of 0.5 cm-1 is obtained (Full-Width
at Half-Maximum).
C.6 Instrument Overview
Launched into a polar sun-syonchronous orbit in 2006, the Infrared Atmospheric Sounding
Interferometer IASI is one of eight instruments on board of the MetOp-A satellite, part of the
Eumetsat Polar System (EPS). It shares the satellite with the following meteorological ins-
truments ([2]) : High resolution Infrared Radiation Sounder, HIRS, Advanced SCATteromter,
ASCAT, Advanced Very High Resolution Radiometer, AVHRR, Microwave Humidity Sounder,
MHS, Advanced Microwave Sounding Unit-A, AMSU-A, and the other advanced atmospheric
chemistry passive remote sensor GOME-2 (for Global Ozone Monitoring Experiment-2).
Looking at the Thermal InfraRed spectral range, MetOp satellite is sun-synchronous with a
inclination of 98.7˚ to the equator, at an altitude of ∼817km, it completes an orbit in about 101
min (more than 14 orbits a day). At nadir, 2×2 circular pixels, 12 km diameter each, correspond
to a field-of-view of 3.3˚×3.3˚ or 50×50 km. This is repeated 15 times on each side of the trace
over a swath width of around 2×1100 km (i.e. 48.3˚ on both sides, see figure C.1). However,
the swaths do not overlap at low latitudes so that some points are missed near the equator for a
short time.
106](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-106-320.jpg)

![Annexe D
Quelques lignes de code
D.1 Code IDL
D.1.1 Récupération des données
La plupart des fonctions décrites ci-dessous visent à obtenir une matrice de 6 ou 10 colonnes.
Les deux premières colonnes correspondent aux latitudes et longitudes, alors que les suivantes
correspondent aux colonnes partielles et la colonne totale (4 colonnes), et si les données le
permettent, avec les erreurs correspondantes (10 colonnes).
Lecture EUMETSAT
;—-Lecture du fichier correspondant.
FUNCTION lecture_data, directory
IF directory EQ ” THEN RETURN, 0
OIASI_L2 = read_eps(directory)
result=OIASI_L2->readProduct()
OIASI_L2->GetRecord,MPHR=mphr
OIASI_L2->GetProperty,MDR=mdr,GIADR1=giadr1
nbre_IFOV = 120.
mTot = MAKE_ARRAY(6, N_ELEMENTS(*mdr)*nbre_IFOV)
M_o3 = 47.9982
M_air = 28.965338
g = 9.81
P0 = (*giadr1)(0).PRESSURE_LEVELS_OZONE[1,1]/10.ˆ2
Pr = (*giadr1)(0).PRESSURE_LEVELS_OZONE[0,*]/10.ˆ2
FOR i=0,N_ELEMENTS(*mdr)-1 DO BEGIN
;—-Boucle sur le nombre d’IFOV (120)
FOR j=0,nbre_IFOV-1 DO BEGIN
;—-Masque nuageux.
IF (*((*mdr)(i))).NUMBER_CLOUD_FORMATIONS[j] EQ 0 THEN BEGIN
;—-Recuperation en kg/m2 des valeurs d’ozone.
Oz = (*((*mdr)(i))).ATMOSPHERIC_OZONE[*,j]/10.ˆ6
IF Oz[0] NE Oz[1] THEN BEGIN
;—-Recuperation des [lat,lon] et conversion en Dobsons.
mTot[*,i*nbre_IFOV+j]=[(*((*mdr)(i))).EARTH_LOCATION[0,j]/10.ˆ4,$
(*((*mdr)(i))).EARTH_LOCATION[1,j]/10.ˆ4,$
Oz[0]*46693.6681,Oz[1]*46693.6681,$
Oz[2]*46693.6681,Oz[3]*46693.6681]
108](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-108-320.jpg)
![ENDIF
ENDIF
EDNFOR
ENDFOR
mTemp = mTot(*,1 :(SIZE(mTot))(2)-1)
OBJ_DESTROY, OIASI_L2
RETURN, mTemp
END
Lecture LATMOS-ULB
;—-Lecture du fichier correspondant.
FUNCTION lecture_err, fichier
CLOSE,/all
OPENR, lun, fichier, /get_lun
lignes = FILES_LINES(fichier)
MatULB = MAKE_ARRAY(1684,lignes)
READF, lun, MatULB
FREE_LUN, lun
P0 = 101325.
trop = 19
Pres = FLTARR(41)
;—-Definition de la pression (cf equations 4.1 et 4.2).
FOR k =0,trop DO BEGIN
Pres(k) = P0*((288-0.0065*k*1e3)/288.)ˆ5.255
ENDFOR
FOR k=trop+1,39 DO BEGIN
Pres(k) = Pres(trop)*EXP(-(k-trop)/8.4)
ENDFOR
Pres(40) = 0.5
M_o3 = 47.9982
M_air = 28.965338
g = 9.81
Mat = INDGEN(10)
FOR i=0.,lignes-1 DO BEGIN
IF MatULB(3,i) GT 90 THEN BEGIN
X_r = MatULB(4 :43,i)
Err = MatULB(44 :83,i)
;—-Elimination des valeurs -999.
IF (WHERE(X_r LT 0))(0) NE -1 THEN X_r([WHERE(X_r LT 0)]) = 0
IF (WHERE(Err LT 0))(0) NE -1 THEN Err([WHERE(Err LT 0)]) = 0
FOR k=0,39 DO BEGIN
X_r(k) = X_r(k)*(Pres(k)-Pres(k+1))*M_o3/(g*M_air)*46693.6681*10.ˆ(-9)
Err(k) = X_r(k)*Err(k)
ENDFOR
moy06 = TOTAL(X_r(0 :5))
err06 = TOTAL(Err(0 :5))
moy012 = TOTAL(X_r(0 :11))
err012 = TOTAL(Err(0 :11))
109](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-109-320.jpg)
![moy018 = TOTAL(X_r(0 :17))
err018 = TOTAL(Err(0 :17))
moy100 = TOTAL(X_r)
err100 = TOTAL(Err)
Mat = [[Mat],[MatULB(0,i),MatULB(1,i),moy06,err06,$
moy012,err012,$
moy018,err018,$
moy100,err100]]
ENDIF
ENDFOR
Mat = Mat(*,1 :(SIZE(mat))(2)-1)
RETURN, Mat
END
Lecture MIPAS
;—-Lecture du fichier correspondant.
;—-Necessite : go_section.pro
FUNCTION write_colpart_stddev, file
OPENR, unit, file, /get_lun
iwarn = go_section(1, 2, 0, 0, unit=unit)
n_tot = 0.0
;—-Recuperation du nombre de point
READF, unit, n_tot
FREE_LUN, unit
mTot = FLTARR(10, n_tot)
FOR i=1,n_tot DO BEGIN
OPENR, unit, file, /get_lun
iwarn = go_section(2, i, 2, unit=unit)
tmp = [0.0, 0.0]
;—-Recuperation du couple [latitude,longitude]
READF, unit, tmp
iwarn = go_section(2, i, 10, unit=unit)
n_grid = 0.0
;—-Recuperation du nombre de niveaux (z)
READF, unit, n_grid
iwarn = go_section(2, i, 11, unit=unit)
Mat = FLTARR(8, n_grid)
READF, unit, Mat
X = FLTARR(60)
Xstd = FLTARR(60)
FOR j = 0,n_grid-2 DO BEGIN
IF Mat(0,j) NE 0 THEN BEGIN
;—-0.0078914 = Mo3/(g*Mair)*f
X(j) = ((Mat(4,j)+Mat(4,j+1))/2)*(Mat(2,j)-Mat(2,j+1))*0.0078914*10.ˆ2
Xstd(j) = ((Mat(5,j)+Mat(5,j+1))/2)*(Mat(2,j)-Mat(2,j+1))*0.0078914*10.ˆ2
ENDIF
ENDFOR
tot = [tmp[0],tmp[1],TOTAL(X(0 :3)),TOTAL(Xstd(0 :3)),$
TOTAL(X(0 :9)),TOTAL(Xstd(0 :9)),$
110](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-110-320.jpg)
![TOTAL(X(0 :15)),TOTAL(Xstd(0 :15)),$
TOTAL(X),TOTAL(Xstd)]
mTot[*,i-1]=tot
FREE_LUN, unit
CLOSE, /all
ENDFOR
RETURN, mTot
END
Lecture CNRM
Les données CNRM fournies sont trop volumineuses pour être traitées directement avec
IDL. Il a fallu les découper au préalable. Pour cela, le logiciel CDO a été très utile. Il peut
en effet traiter des données très importantes sans prendre toute la mémoire de l’ordinateur. La
simple commande à entrer sur l’invite de commandes (cas Windows) est la suivante :
cdo splitmon o_3_h.M8.2000.nc o_3_2000
Ici, o_3_h.M8.2000.nc est le fichier source d’environ 1 Go, o_3_2000 est la base de nom qu’au-
ront tous les fichiers issus de cette commande splitmon.
FUNCTION lecture_CNRM_O3, date
CLOSE, /ALL
;—-Conversion de la date pour recuperer les donnes correspondantes.
yyyymmdd = LONG(date)
year_n = yyyymmdd/10ˆ4
year = STRCOMPRESS(STRING(year_n),/REMOVE_ALL)
month_n = (yyyymmdd-year_n*10ˆ4)/10ˆ2
IF month_n LT 10 THEN month = STRCOMPRESS(’0’+STRING(month_n),/REMOVE_ALL) $
ELSE month = STRCOMPRESS(STRING(month_n),/REMOVE_ALL)
day_n = yyyymmdd-year_n*10ˆ4-month_n*10ˆ2
IF day_n LT 10 THEN day = STRCOMPRESS(’0’+STRING(day_n),/REMOVE_ALL) $
ELSE day = STRCOMPRESS(STRING(day_n),/REMOVE_ALL)
O3ID = NCDF_OPEN(’D :PUBLICCDOo_3_2000’+month+’.nc’)
PID = NCDF_OPEN(’D :PUBLICCDOpres_2000’+month+’.nc’)
;—-Recuperation de la pression.
varstructP = NCDF_VARINQ(PID,4)
varIDP = NCDF_VARID(PID,varstructP.name)
NCDF_VARGET,PID,varIDP,variableP
nMlon = (SIZE(variableP))(1)
nMlat = (SIZE(variableP))(2)
nMh = (SIZE(variableP))(3)
;—-Recuperation de l’ozone.
varstruct = NCDF_VARINQ(O3ID,3)
varID=NCDF_VARID(O3ID,varstruct.name)
NCDF_VARGET,O3ID,varID,variable
M_o3 = 47.9982
M_air = 28.965338
g = 9.81
Mat = MAKE_ARRAY(6,1)
varstructLAT = NCDF_VARINQ(O3ID,1)
varIDLAT=NCDF_VARID(O3ID,varstructLAT.name)
NCDF_VARGET,O3ID,varIDLAT,variableLAT
111](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-111-320.jpg)
![varstructLON = NCDF_VARINQ(O3ID,0)
varIDLON=NCDF_VARID(O3ID,varstructLON.name)
NCDF_VARGET,O3ID,varIDLON,variableLON
varstructO3 = NCDF_VARINQ(O3ID,4)
varIDO3=NCDF_VARID(O3ID,varstructO3.name)
NCDF_VARGET,O3ID,varIDO3,variableO3
temp = day_n-1
FOR nlat = 0,nMlat-1 DO BEGIN
FOR nlon = 0,nMlon-1 DO BEGIN
O3 = variableO3(nlon,nlat,*,temp)
P = variableP(nlon,nlat,*,temp)
tp = MAKE_ARRAY(nMh-1)
FOR j = 0,nMh-1-1 DO BEGIN
;—-Conversion de l’ozone [ppm] en Dobson avec la pression.
tp(j) = O3(j)*(P(j)-P(j+1))*M_o3/(g*M_air)*46641.59
ENDFOR
IF variableLON(nlon) GT 180 THEN BEGIN
longitude = variableLON(nlon)-360
ENDIF ELSE BEGIN
longitude = variableLON(nlon)
ENDELSE
Mat = [[Mat],[variableLAT(nlat),longitude,TOTAL(tp(0 :5)),TOTAL(tp(0 :11)),$
TOTAL(tp(0 :17)),TOTAL(tp)]]
ENDFOR
ENDFOR
;—-Elimination de la premiere ligne.
Mat = Mat[*,1 :(SIZE(Mat))(2)-1]
NCDF_CLOSE, O3ID
NCDF_CLOSE, PID
RETURN, Mat
END
D.1.2 Récupération LATMOS-ULB à partir des pressions EUMETSAT
;—-Recuperation des donnees LATMOS-ULB.
Result = FILE_SEARCH(’D :PUBLICData_ULB*’)
Res = Result([WHERE(STRMATCH(Result,’*20080831*’) EQ 1)])
mTot=INDGEN(42)
n_col = (SIZE(Res))(1)
M_o3 = 47.9982
M_air = 28.965338
g = 9.81
mat = INDGEN(10)
LATMOS-ULB = MAKE_ARRAY(84)
FOR fi=0,n_col-1 DO BEGIN
fichier = Res(fi)
OPENR, lun, fichier, /get_lun
lignes = FILE_LINES(fichier)
MatULB = MAKE_ARRAY(1684,lignes)
READF, lun, MatULB
112](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-112-320.jpg)
![FREE_LUN, lun
LATMOS-ULB = [[LATMOS-ULB],[MatULB(0 :83,*)]]
ENDFOR
LATMOS-ULB = LATMOS-ULB(*,1 :(SIZE(LATMOS-ULB))(2)-1)
;—-Ouverture EUMETSAT
Result = FILE_SEARCH(’D :PUBLICData_Eumetsat*’)
Res = Result([WHERE(STRMATCH(Result,’*20080831*’) EQ 1)])
mTot=INDGEN(42)]
n_col = (SIZE(Res))(1)
nbre_IFOV = 120.
g = 9.80665
M = 28.965338
R = 8.314462
FOR fi=0,n_col-1 DO BEGIN
directory = Res(fi)
OIASI_L2 = read_eps(directory)
result=OIASI_L2->readProduct()
OIASI_L2->GetRecord,MPHR=mphr
OIASI_L2->GetProperty,MDR=mdr,GIADR1=giadr1
A = INDGEN(80)
FOR i=0,N_ELEMENTS(*mdr)-1 DO BEGIN
;—-Recuperation de la pression
P = REVERSE((*giadr1)(0).PRESSURE_LEVELS_TEMP)/10.ˆ2
;—-Recuperation de la temperature
T = REVERSE((*((*mdr)(i))).ATMOSPHERIC_TEMPERATURE/10.ˆ2)
FOR j=0,nbre_IFOV-1 DO BEGIN
;—-Condition sur la couverture nuageuse
IF (*((*mdr)(i))).NUMBER_CLOUD_FORMATIONS[j] EQ 0 THEN BEGIN
;—-Condition sur l’existence du profil de temperature
IF (T(*,j))(89) NE 655.350 THEN BEGIN
Oz = (*((*mdr)(i))).ATMOSPHERIC_OZONE[*,j]/10.ˆ6
;—-Condition sur l’existence des colonnes partielles
IF Oz[0] NE Oz[1] THEN BEGIN
lat = (*((*mdr)(i))).EARTH_LOCATION[0,j]/10.ˆ4
lon = (*((*mdr)(i))).EARTH_LOCATION[1,j]/10.ˆ4
;—-Recherche des points [lat,lon]identiques
loc = WHERE(LATMOS-ULB(0,*) EQ lat AND LATMOS-ULB(1,*) EQ lon)
;—-Condition sur la correspondance des points
IF loc(0) NE -1 THEN BEGIN
;—-Recuperation de la pression de surface
P0 = (*((*mdr)(i))).SURFACE_PRESSURE(j)
;—-Suppression des niveaux ou la temperature n’est pas disponible
cas = WHERE(T(*,j) NE 655.350)
Pres = P
IF cas(0) NE -1 THEN Pres = (P)(WHERE(T(*,j) NE 655.350))
Temp = T(*,j)
IF cas(0) NE -1 THEN Temp = (T(*,j))(WHERE(T(*,j) NE 655.350))
;—-Calcul de l’altitude pour les niveaux de pressions et temperature
Z = -(R*Temp/(M*g))*ALOG(Pres/P0)
;—-Interpolation de la temperature aux altitudes 0, 1, 2, 3... 39km.
113](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-113-320.jpg)
![Result = INTERPOL(Temp,Z,A)
;—-Recuperation de la pression a ces altitudes
NewP = P0*EXP(-1.*M*g*A/(R*Result))
;—-Ajout de la pression top of the atmosphere = 0.5 Pa
NewP = [NewP,0.5]
;—-recuperation du profil de [ppb]
X_r = FLTARR(80)
X_r(0 :39) = LATMOS-ULB(4 :43,loc)
X_r(40 :79) = LATMOS-ULB(43,loc)
;—-et de l’erreur
Err = FLTARR(80)
Err(0 :39) = LATMOS-ULB(44 :83,loc)
Err(40 :79) = LATMOS-ULB(83,loc)
;—-suppression des -999 (orographie)
IF (WHERE(X_r LT 0))(0) NE -1 THEN X_r([WHERE(X_r LT 0)]) = 0
IF (WHERE(Err LT 0))(0) NE -1 THEN Err([WHERE(Err LT 0)]) = 0
FOR k=0,79 DO BEGIN
;—-Calcul des colonnes partielles en DU
X_r(k) = X_r(k)*M_o3*NewP(k)/(R*Result(k))*46696.241*10.ˆ(-9)
Err(k) = X_r(k)*Err(k)
ENDFOR
moy06 = TOTAL(X_r(0 :5))
err06 = TOTAL(Err(0 :5))
moy012 = TOTAL(X_r(0 :11))
err012 = TOTAL(Err(0 :11))
moy018 = TOTAL(X_r(0 :17))
err018 = TOTAL(Err(0 :17))
moy100 = TOTAL(X_r)
err100 = TOTAL(Err)
mat = [[mat],[LATMOS-ULB(0,loc),LATMOS-ULB(1,loc),moy06,err06,moy012,err0
moy018,err018,moy100,er
ENDIF
ENDIF
ENDIF
ENDIF
ENDFOR
ENDFOR
ENDFOR
mat = mat(*,1 :(SIZE(mat))(2)-1)
D.2 Création du logiciel de comparaison
D.2.1 Création de la grille
;—-Creation d’une grille [-180 ;-90 ;180 ;90] par pas de 1.4˚.
FUNCTION creation_grille,Mat
Mfin = [INDGEN(6)]
pas = 1.4
FOR i = -90.,90.,pas DO BEGIN
114](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-114-320.jpg)
![FOR j = -180.,180.,pas DO BEGIN
;—-Valeur par defaut : -999.
moy1 = -999.
moy2 = -999.
moy3 = -999.
moy4 = -999.
X1 = Mat(*,[WHERE (Mat[0,*]-i LT pas/2. AND Mat[0,*]-i GT -pas/2. $
AND Mat[1,*]-j LT pas/2. AND Mat[1,*]-j GT -pas/2.,count)])
IF count NE 0 THEN BEGIN
moy1 = MEAN(X1[2,*])
moy2 = MEAN(X1[3,*])
moy3 = MEAN(X1[4,*])
moy4 = MEAN(X1[5,*])
ENDIF
Mfin = [[Mfin],[i,j,moy1,moy2,moy3,moy4]]
ENDFOR
ENDFOR
;—-Elimination de la premiere ligne.
Mfin = Mfin[*,1 :(SIZE(Mfin))(2)-1]
RETURN, Mfin
END
D.2.2 Création sous format netCDF
;—-Creation sous le format netCDF
FUNCTION creation_ncdf, Mat_Eumetsat,date,dossier_sortie,Origine
A = -90
FOR i = -90.+1.4,90,1.4 DO BEGIN
A = [A,i]
ENDFOR
B = -180
FOR i = -180.+1.4,180,1.4 DO BEGIN
B = [B,i]
ENDFOR
C = [6,12,18,100]
id = NCDF_CREATE(dossier_sortie+’’+date+’_O3_’+Origine+’.nc’,/CLOBBER)
NCDF_CONTROL, id, /FILL
lat = NCDF_DIMDEF(id,’Latitude’, 129)
lon = NCDF_DIMDEF(id, ’Longitude’, 258)
z = NCDF_DIMDEF(id, ’Ozone_Column’, /UNLIMITED)
O3 = NCDF_DIMDEF(id, ’Ozone’, 129.*258*4)
latid = NCDF_VARDEF(id,’Latitude’,[lat],/FLOAT)
lonid = NCDF_VARDEF(id,’Longitude’,[lon],/FLOAT)
zid = NCDF_VARDEF(id,’Ozone_column’,[z],/FLOAT)
O3id = NCDF_VARDEF(id,’Ozone’,[lat,lon,z],/FLOAT)
NCDF_ATTPUT, id, latid, ’long_name’, ’Latitude’
NCDF_ATTPUT, id, latid, ’units’, ’Degrees’
NCDF_ATTPUT, id, latid, ’axis’, ’y’
NCDF_ATTPUT, id, lonid, ’long_name’, ’Longitude’
NCDF_ATTPUT, id, lonid, ’units’, ’Degrees’
115](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-115-320.jpg)
![NCDF_ATTPUT, id, lonid, ’axis’, ’x’
NCDF_ATTPUT, id, zid, ’units’, ’km’
NCDF_ATTPUT, id, zid, ’long_name’, ’Height of column’
NCDF_ATTPUT, id, zid, ’axis’, ’z’
NCDF_ATTPUT, id, O3id, ’units’, ’Dobson Units’
NCDF_ATTPUT, id, /GLOBAL, ’Title’, ’Partial and total columns of Ozone [DU] of ’+date+’.’
NCDF_CONTROL, id, /ENDEF
NCDF_VARPUT, id, latid, A
NCDF_VARPUT, id, lonid, B
NCDF_VARPUT, id, zid, C
FOR h = 0.,4-1 DO BEGIN
FOR j = 0.,129-1 DO BEGIN
NCDF_VARPUT, id, O3id, Mat_Eumetsat(h+2,0+j*258 :258-1+j*258), OFFSET=[j,0,h]
ENDFOR
ENDFOR
NCDF_CLOSE, id
END
D.2.3 Comparaison des profils/histogrammes
FUNCTION histo_EvsC,Mat_Eum,Mat_CNRM
col = 5
loc = WHERE(Mat_CNRM(col,*) NE -999)
loc2 = WHERE(Mat_Eum(col,*) NE -999)
;—-Cas de la selection des latitudes > -60 ˚.
;loc = WHERE(Mat_CNRM(col,*) NE -999 AND Mat_CNRM(0,*) GT -60)
;loc2 = WHERE(Mat_Eum(col,*) NE -999 AND Mat_Eum(0,*) GT -60)
minval = MIN([MIN(Mat_CNRM(col,loc)),MIN(Mat_Eum(col,loc2))])
maxval = MAX(Mat_Eum(col,loc2))
;—-Calcul des moyennes et ecarts-types pour Eum et CNRM
mg = MEAN(Mat_CNRM(col,loc))
m = MEAN(Mat_Eum(col,loc2))
sg = STDDEV(Mat_CNRM(col,loc))
s = STDDEV(Mat_Eum(col,loc2))
countG = MAKE_ARRAY(2)
count = MAKE_ARRAY(2)
FOR i=minval,maxval DO BEGIN
;—-Recuperation du nombre d’element entre i et i+1, ramene au nombre total d’element.
count = [[count],[i,(N_ELEMENTS(WHEREMat_Eum(col,loc2) GT i AND $
Mat_Eum(col,loc2) LE i+1))*100./N_ELEMENTS(loc2)]]
countG = [[countG],[i,(N_ELEMENTS(WHERE(Mat_CNRM(col,loc) GT i AND $
Mat_CNRM(col,loc) LE i+1))*100./N_ELEMENTS(loc)]]
ENDFOR
count = count(*,1 :(SIZE(count))(2)-1)
countG = countG(*,1 :(SIZE(countG))(2)-1)
A = INDGEN(MAX(count)+100)
WINDOW,0,XSIZE=400,YSIZE=300
!P.FONT=0
!P.MULTI=[0,1,0,0,0]
;—-Plot pour EUMETSAT
116](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-116-320.jpg)
![PLOT, count(0,*),count(1,*),BACKGROUND=-1,COLOR=0,XRANGE=[0,400],$
XTITLE=’Colonne Totale [DU]’,TITLE=’EUMETSAT vs CNRM’,$
POSITION=[0.05,0.11,0.95,0.91],YTICKINTERVAL=1
;—-Avec les barres verticales de la moyenne + ou - l’ecart type
OPLOT,A*0+m,A,LINESTYLE=3,COLOR=0
OPLOT,A*0+m-s,A,LINESTYLE=1,COLOR=0
OPLOT,A*0+m+s,A,LINESTYLE=1,COLOR=0
;—-De meme pour les donnes CNRM, changement de couleur
OPLOT, countG(0,*),countG(1,*),COLOR=250*250*249
OPLOT,A*0+mg,A,LINESTYLE=3,COLOR=250*250*249
OPLOT,A*0+mg-sg,A,LINESTYLE=1,COLOR=250*250*249
OPLOT,A*0+mg+sg,A,LINESTYLE=1,COLOR=250*250*249
PRINT, ’Stat EUMETSAT =’,m,s
PRINT, ’Stat CNRM =’,mg,sg
PRINT, ’Variation =’,(m-mg)*100./m-100,(s-sg)*100./s-100
RETURN, count
END
D.2.4 Création des cartes
Pour créer la carte à partir d’une matrice, on procède à une répartition sur grille temporaire.
Cependant, pour des raisons d’affichage, il est utile d’établir la grille de manière différente. En
effet, dans le cas normal pour créer une carte, le logiciel IDL va colorer le carré dont 4 points
en formeront les sommets. Si l’un des points est absents, seul un triangle sera coloré. Et si deux
points sont absents, c’est juste un trait qui apparaîtra, ce qui n’est pas forcément visible sur une
grille de l’ordre de 180 éléments par 360.
Ici, je décris une méthode qui va permettre d’afficher tous les points présents de la grille. Il
faut bien comprendre que la grille ou les données qui servent aux calculs ne sont pas modifiées,
mais seulement la grille temporaire concernée par l’affichage. Pour ce faire, la méthode est bien
simple : un point va contaminer de sa valeur les 4 points de la maille qui l’entoure. Et si l’un
des sommets a déjà été assimilé à une valeur, le programme fait la moyenne des points qui y
sont présents.
;—-Necessite : contour_on_map.pro, colorbar.pro, fsc_color.pro
FUNCTION creation_JPEG_mat_NoCumul, Mat1, pas, jour
lines = (SIZE(Mat1))(2)
lat = -89.999
FOR i = -89.999+pas,90,pas DO BEGIN
lat = [lat,i]
ENDFOR
lon = -179.999
FOR i = -179.999+pas,180,pas DO BEGIN
lon = [lon,i]
ENDFOR
;—-Matrice de la somme des quantites d’ozone, taille longitude×latitude.
Mat = MAKE_ARRAY(FIX((180+179.999)/pas)+1,FIX((90+89.999)/pas)+1)
;—-Matrice du nombre de points contribuant.
Matc = MAKE_ARRAY(FIX((180+179.999)/pas)+1,FIX((90+89.999)/pas)+1)+1.
;—-Boucle sur le nombre de lignes.
FOR i = 0.,lines-1 DO BEGIN
117](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-117-320.jpg)
![;—-Recuperation des 4 sommets [a,b,c,d].
loclat1 = WHERE(lat-Mat1(0,i) GT 0)
a = loclat1(0)
loclat2 = WHERE(-(lat-Mat1(0,i)) GT 0)
b = loclat2(N_ELEMENTS(loclat2)-1)
loclon1 = WHERE(lon-Mat1(1,i) GT 0)
c = loclon1(0)
loclon2 = WHERE(-(lon-Mat1(1,i)) GT 0)
d = loclon2(N_ELEMENTS(loclon2)-1)
IF a EQ -1 || b EQ -1 || c EQ -1 || d EQ -1 THEN BEGIN
ENDIF ELSE BEGIN
IF Mat(c,a) NE 0 THEN BEGIN
Mat(c,a) = TOTAL([Mat(c,a),Mat1(5,i)],/NAN)
Matc(c,a) = Matc(c,a)+1
ENDIF ELSE BEGIN
Mat(c,a) = Mat1(5,i)
Matc(c,a) = 1
ENDELSE
IF Mat(d,a) NE 0 THEN BEGIN
Mat(d,a) = TOTAL([Mat(d,a),Mat1(5,i)],/NAN)
Matc(d,a) = Matc(d,a)+1
ENDIF ELSE BEGIN
Mat(d,a) = Mat1(5,i)
Matc(d,a) = 1
ENDELSE
IF Mat(c,b) NE 0 THEN BEGIN
Mat(c,b) = TOTAL([Mat(c,b),Mat1(5,i)],/NAN)
Matc(c,b) = Matc(c,b)+1
ENDIF ELSE BEGIN
Mat(c,b) = Mat1(5,i)
Matc(c,b) = 1
ENDELSE
IF Mat(d,b) NE 0 THEN BEGIN
Mat(d,b) = TOTAL([Mat(d,b),Mat1(5,i)],/NAN)
Matc(d,b) = Matc(d,b)+1
ENDIF ELSE BEGIN
Mat(d,b) = Mat1(5,i)
Matc(d,b) = 1
ENDELSE
ENDELSE
ENDFOR
;—-Calcul de la matrice, moyenne points par points.
Mat = Mat/Matc
IF (WHERE(Mat EQ 0))(0) NE -1 THEN Mat[WHERE(Mat EQ 0)] = !Values.F_NAN
;—-Nombre d’elements F_NAN.
nNANtot = N_ELEMENTS(WHERE(FINITE(Mat, /NAN)))
IF (WHERE(FINITE(Mat, /NAN)))(0) EQ -1 THEN nNANtot = 0
;—-Calcul du pourcentage de la carte recouverte par les donnees.
percent = (N_ELEMENTS(Mat)-nNANtot)*100./N_ELEMENTS(Mat)
contour_on_map, lon, lat, Mat, ct=26,latrange=[-90,90],lonrange=[-180,180],ncolors=15,$
118](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-118-320.jpg)
![cbar_title=’CNRM Total ozone [DU] (2008_09_’+jour+’)’,$
xsize=1000,ysize=650,POSITION=[0.05,0.15,0.95,0.95],$
c_position=[0.05,0.05,0.95,0.08],$
colorbar_min=0,colorbar_max=400
END
D.2.5 Noyau de la fonction
Base
PREF_SET, &
’IDL_PATH’, ’+D :PUBLICData_Comparison ;<IDL_DEFAULT>’,/COMMIT
;—-Format date : yyyymmdd -> renvoi year_n/year, etc, suivant le besoin de int ou string
date = STRCOMPRESS(STRING(yyyymmdd),/REMOVE_ALL)
year_n = yyyymmdd/10ˆ4
year = STRCOMPRESS(STRING(year_n),/REMOVE_ALL)
month_n = (yyyymmdd-year_n*10ˆ4)/10ˆ2
IF month_n LT 10 THEN month = STRCOMPRESS(’0’+STRING(month_n),/REMOVE_ALL) &
ELSE month = STRCOMPRESS(STRING(month_n),/REMOVE_ALL)
day_n = yyyymmdd-year_n*10ˆ4-month_n*10ˆ2
IF day_n LT 10 THEN day = STRCOMPRESS(’0’+STRING(day_n),/REMOVE_ALL) &
ELSE day = STRCOMPRESS(STRING(day_n),/REMOVE_ALL)
;—-creation du dossier de sortie des donnees
dossier_sortie = STRCOMPRESS(’D :PUBLICData_ComparisonTest_’&
+year+’_’+month+’_’+day,/REMOVE_ALL)
FILE_MKDIR, dossier_sortie
;—-Appel des donnees correspondantes
Mat_Eum = creation_txt_Eumetsat(date,dossier_sortie)
EUMETSAT_ncdf = creation_ncdf(Mat_Eum,date,dossier_sortie,’EUMETSAT’)
Mat_LATMOS-ULB = creation_txt_ULB(date,dossier_sortie)
Mat_MIPAS = creation_txt_MIPAS_std(date,dossier_sortie)
;—-Condition sur l’existence du jour MIPAS
IF Mat_MIPAS(0) NE -1 THEN &
MIPAS_ncdf = creation_ncdf(Mat_MIPAS,date,dossier_sortie,’MIPAS’)
Mat_CNRM = creation_txt_CNRM(date,dossier_sortie)
Sous-fonctions appelées.
;—-EUMETSAT
FUNCTION creation_txt_Eumetsat, date,dossier_sortie
PREF_SET, &
’IDL_PATH’, ’+D :PUBLICData_EumetsatLecture ;<IDL_DEFAULT>’,/COMMIT
CLOSE,/ALL
Result = FILE_SEARCH(’D :PUBLICData_Eumetsat*’)
Res = Result([WHERE(STRMATCH(Result,’*’+date+’*’) EQ 1)])
matTot=INDGEN(6)
n_col = (SIZE(Res))(1)
FOR i=0,n_col-1 DO BEGIN
fichier = Res(i)
119](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-119-320.jpg)
![matTemp = lecture_data(fichier)
matTot = [[matTot],[matTemp]]
ENDFOR
matTot = matTot(*,1 :(SIZE(matTot))(2)-1)
;—-Ecriture des fichiers .txt qui serviront a la comparaison et aux statistiques
OPENW, 1, STRCOMPRESS(dossier_sortie+’’+date+’_Eumetsat.txt’,/REMOVE_ALL)
PRINTF, 1, matTot
CLOSE, 1
;—-Creation de la grille associee a la matrice
Mgrid = creation_grille(matTot)
OPENW, 1, STRCOMPRESS(dossier_sortie+’’+date+’_Eumetsat_grid.txt’,/REMOVE_ALL)
PRINTF, 1, Mgrid
CLOSE, 1
PREF_SET, ’IDL_PATH’, /DEFAULT
RETURN, Mgrid
END
;—-LATMOS-ULB
FUNCTION creation_txt_ULB, date,dossier_sortie
PREF_SET,&
’IDL_PATH’, ’+D :PUBLICData_ULBLecture_ULB ;<IDL_DEFAULT>’,/COMMIT
CLOSE,/ALL
Result = FILE_SEARCH(’D :PUBLICData_ULB’)
Res = STRCOMPRESS(Result([WHERE(STRMATCH(Result,’*’+date+’*’) EQ 1)]),$
/REMOVE_ALL)
n_col = (SIZE(Res))(1)
Mat = INDGEN(10)
FOR i=0,n_col-1 DO BEGIN
fichier = Res(i)
MaTemp = lecture_err(fichier)
Mat = [[Mat],[MaTemp]]
ENDFOR
Mat = Mat(*,1 :(SIZE(Mat))(2)-1)
OPENW, 1, STRCOMPRESS(dossier_sortie+’’+date+’_LATMOS-ULB_err.txt’,&
/REMOVE_ALL),WIDTH=250
PRINTF, 1, Mat
CLOSE, 1
Mgrid = creation_grille(Mat)
OPENW, 1, STRCOMPRESS(dossier_sortie+’’+date+’_LATMOS-ULB_grid.txt’,/REMOVE_ALL)
PRINTF, 1, Mgrid
CLOSE, 1
PREF_SET, ’IDL_PATH’, /DEFAULT
RETURN, Mgrid
END
;—-MIPAS
FUNCTION creation_txt_MIPAS_std, date,dossier_sortie
PREF_SET,&
’IDL_PATH’, ’+D :PUBLICData_MIPASIDL_routines ;<IDL_DEFAULT>’,/COMMIT
CLOSE,/ALL
120](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-120-320.jpg)
![Result = FILE_SEARCH(’D :PUBLICData_MIPAS’)
Res = STRCOMPRESS(Result([WHERE(STRMATCH(Result,’*’+date+’*’) EQ 1)]),&
/REMOVE_ALL)
;—-Condition sur l’existence du jour
IF (WHERE(STRMATCH(Result,’*’+date+’*’) EQ 1))(0) EQ -1 THEN BEGIN
PRINT, ’Absence de donnees pour la journee ’+date+’.’
;—-Possibilite de recuperer une autre journee
;Res = dialog_pickfile(/read)
Mgrid = -1
ENDIF ELSE BEGIN
Mat = INDGEN(10)
FOR i = 0,(size(Res))(3)-1 DO BEGIN
fichier = Res(i)
matTemp = write_colpart_stddev(fichier)
Mat = [[Mat],[matTemp]]
ENDFOR
Mat = Mat(*,1 :(SIZE(Mat))(2)-1)
OPENW, 1, STRCOMPRESS(dossier_sortie+’’+date+’_MIPAS_std.txt’,&
/REMOVE_ALL),WIDTH=250
PRINTF, 1, Mat
CLOSE, 1
Mgrid = creation_grille_std(Mat)
OPENW, 1, STRCOMPRESS(dossier_sortie+’’+date+’_MIPAS_grid_std.txt’,&
/REMOVE_ALL),WIDTH=250
PRINTF, 1, Mgrid
CLOSE, 1
PREF_SET, ’IDL_PATH’, /DEFAULT
ENDELSE
RETURN, Mgrid
END
Pour les données CNRM et la création du format NetCDF, ce sont les fonctions lecture_CNRM_O3
et creation_ncdf déjà décrites précédemment qui sont appelées.
121](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-121-320.jpg)

![E.2 Temps de calcul
E.2.1 Récupération LATMOS-ULB
Version 1
Les données LATMOS-ULB sont stockées et comprimées dans un fichier .tar, lui même
contenant une quinzaine de fichier .bz2 pour chaque orbite. Si le taux de compression est de
100% pour le premier échelon, il est de 24% pour le second. Ainsi, les données brutes pesant
∼ 8 Go sont comprimées à ∼ 2 Go avant l’extraction. Ce qui prend le plus temps est justement
l’extraction des 15 fichiers des orbites. Il faut compter environ 1 heure pour l’extraction et
ensuite, dans le cas optimal, 15 minutes pour lire et créer le fichier .txt de la journée considérée.
Version 2
Dans ce cas, les données du LATMOS-ULB sont couplées aux données d’EUMETSAT.
Pour lire une journée, il faut donc lire la même journée sur les 2 sources, comme l’explicite
le code D.1.2. De plus, la recherche des couples [latitude,longitude] identiques, la récupération
des profils de température et pression avec le calcul de l’altitude et surtout l’interpolation de
la température sur d’autres niveaux d’altitude va allonger considérablement le temps de calcul.
Ainsi, la récupération d’une unique journée prendra environ 2 heures, pour seulement ∼500
points.
E.2.2 Récupération EUMETSAT
Lecture
La lecture des données d’EUMETSAT se fait assez rapidement. Le code établi sous forme
de condition afin de vérifier la validité d’un point va mettre seulement une quinzaine de minutes
à produire la matrice rassemblant toutes les valeurs.
Répartition sur grille
Cependant, c’est au niveau de la répartition sur grille que la récupération des données EU-
METSAT prend le plus de temps. Fortement dépendant de la quantité de points, le temps de
calcul prendra en moyenne 15 à 20 minutes. Lorsque les calculs nécessitent plusieurs jours
(comme une répartition sur grille à partir de jours moyennés), il faut multiplier le temps de
calcul par le nombre de jour. Ainsi, un mois réparti sur grille peut prendre jusqu’à 10 heures
(moyenner les grilles de chaque jour ne serait pas un calcul exact du fait qu’il faudrait alors tenir
compte de la pondération assimilée au nombre de points utilisés pour chaque point de grille).
E.2.3 Récupération MIPAS et CNRM
Pour ces deux jeux de données, la récupération se fait assez rapidement. En effet, le nombre
de points pour les données MIPAS est faible, il suffit alors de quelques minutes pour effectuer
les calculs de conversion entre [ppm] et [Dobsons]. De même, les données CNRM étant déjà
reparties sur une grille avec les niveaux d’altitudes en kilomètres, c’est là aussi une conversion
d’unité qui prendra le temps de récupération, c’est-à-dire quelques minutes.
123](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-123-320.jpg)
![Table des figures
1.1 Satellite MetOp et ses divers instruments l’accompagnant. . . . . . . . . . . . 7
1.2 à gauche, les pincipaux éléments composant l’interféromètre IASI. A droite, le
mode d’osbervation de IASI : l’instrument mesure le spectre infrarouges émis
par la Terre et l’atmosphère sur une largeur d’environ 2200 km, tous les 50 km
au nadir avec 4 empreintes de 12 km de diamètre (crédits images : ESA, CNES) 8
2.1 Structure basique des CCMs incluant la globalité de la science atmosphérique. . 11
2.2 Date de la restitution de l’ozone selon l’année de référence (abscisse) sur diffé-
rentes couches de l’atmosphère décomposée en isobares ([9]). Les zones blanches
correspondent au fait que le modèle moyen ne constate pas de restitution de
l’ozone à la fin de la simulation, c’est-à-dire passé 2094. . . . . . . . . . . . . 14
3.1 Gauche : l’atmosphère terrestre et ses différentes couches (Crédit : Laurence
Jacquenod). Droite : Les couches de l’atmosphère et la moyenne temporelle
des échanges entre elles. La différence entre hémisphère sud et hémisphère nord
est assez marquante et les turbulences dans la troposphère sont aussi mises en
évidence. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
3.3 Répartition de l’ozone dans l’atmosphère, concentré à 90% dans la stratosphère. 23
3.2 Représentation de l’angle zénithal solaire, avec l’angle zénithal de visée (Vie-
wing Zenith Angle, angle entre le satellite et le zénith au point d’observation).
Afin d’observer la surface sous une incidence constante, la somme des deux
angles doit être maintenue durant les observations (Crédit : NASA). . . . . . . 23
3.4 Spectre en radiance IASI normalisé et ses bandes spectrales (Crédit : Eumetsat). 25
4.1 Echantillonnage spatial et temporel. À gauche, l’échantillonnage spatial. À chaque
trait correspond un jour (les 5 premiers jours du mois de septembre 2008), en
noir pour une grille de 1.4˚×1.4˚ et en bleu pour une grille de 2.8125˚×8.125˚
(ici seulement 3 jours). En rouge, la limite du critère de Student, à 1.96. À
droite, l’échantillonnage temporel, sur le mois d’août 2008. . . . . . . . . . . . 33
4.2 Résultats de l’échantillonnage spatial sur carte. En haut, la journée complète du
1er septembre 2008, et en bas, la même journée, mais avec un échantillonnage
spatial de 2. Les différences sont difficilement observables. La couverture est
moins importante sur l’échantillonnage de 2, sans être trop significatif. . . . . . 34
4.3 Résultats de l’échantillonnage temporel sur carte. En haut, les 31 jours du mois
d’août 2008 sur grille moyennés, et en bas, 13 jours du même mois. Le pas
d’échantillonnage est de 2.5, ce qui correspond aux jours suivants : 1, 3, 6, 8,
11, 13, 16, 18, 21, 23, 26, 28 et 31. On observe quelques différences minimes,
les plus nombreuses au niveau des hautes latitudes et de la couverture nuageuse. 35
4.4 Histogrammes des données EUMETSAT et LATMOS-ULB pour différentes
définitions de l’altitude de la tropopause. En tirets sont disposés les moyennes.
En pointillés et traits pleins, les écarts types à 1 σ. . . . . . . . . . . . . . . . . 37
124](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-124-320.jpg)
![4.5 Tables des couleurs utilisées : celle du haut (table IDL 26) correspond à une
représentation directe des valeurs d’ozone (le plus souvent en Dobson, allant
de 200 à 400 Dobsons pour la colonne totale), et celle du bas (table IDL 33)
correspondant à la différence entre deux jeux de données, aussi en unité Dobson. 38
4.6 Différence sur les points identiques des valeurs issues d’EUMETSAT et du
LATMOS-ULB pour une journée (2008_09_01). Seuls les points possédant le
couple [longitude,latitude] strictement identique ont été sélectionnés. En ef-
fet, les données provenant du LATMOS-ULB et d’EUMETSAT sont issues
du même satellite, et donc les coordonnées devraient correspondre. Cependant,
puisque les deux laboratoires procèdent à un retrieval différent et ont des flags
nuageux variables, celles-ci peuvent varier. . . . . . . . . . . . . . . . . . . . 39
4.7 Histogrammes des valeurs des colonnes totales d’ozone entre EUMETSAT (noir)
et LATMOS-ULB (rouge) pour le 1er septembre 2008. En haut à gauche, sur la
totalité du globe, à droite, pour les latitudes inférieures à -45˚, en bas à gauche,
entre -45˚ et 45˚, et à droite, pour les latitudes supérieures à 45˚. . . . . . . . . 40
4.8 Cartes des différences entre EUMETSAT et LATMOS-ULB pour les 3 colonnes
partielles et la colonne totale (valeurs allant de -50 à + 50 Dobson). En haut à
gauche, la colonne partielle [0-6] km. En haut à droite, la colonne partielle [0-
12] km. En bas à gauche, la colonne partielle [0-18] km puis enfin la colonne
totale en bas à droite, similaire à la figure 4.6. . . . . . . . . . . . . . . . . . . 41
4.9 Les nuages de points correspondant à la comparaison entre EUMETSAT et le
LATMOS-ULB pour la journée du 1er septembre 2008. . . . . . . . . . . . . . 42
4.10 Sélection sur des longitudes comprises entre 40 et 45˚ des valeurs d’ozone selon
les latitudes. En haut, pour les colonnes partielles [0-6], [0-12] et [0-18] km, en
bas, sur toute la colonne totale. . . . . . . . . . . . . . . . . . . . . . . . . . . 43
4.11 Carte de la différence entre EUMETSAT et LATMOS-ULB (colonne totale au
1er septembre 2008). Ici sont représentés uniquement les points où la colonne
totale d’EUMETSAT est comprise dans l’écart type de la colonne totale du
LATMOS-ULB. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
4.12 Histogramme des points correspondant à la carte 4.11. La moyenne est d’envi-
ron +7.6 DU, soit un écart positif des valeurs d’EUMETSAT par rapport à celle
du LATMOS-ULB, sur la sélection de points précédement évoquée. . . . . . . 44
4.13 Histogrammes des valeurs en ozone (Dobson) du 1er septembre 2008. En noir,
les données EUMETSAT, en rouge, les données LATMOS-ULB. L’ordonnée
correspond au nombre de points et non au pourcentage de points. Le graphique
de gauche correspond à la journée total, le graphique du milieu à une sélection
des données jour, et le graphique à droite, aux données nuit. . . . . . . . . . . . 45
4.14 À gauche, cartes EUMETSAT et LATMOS-ULB des valeurs en ozone du 1er
septembre 2008 (échelle de 200 à 400 Dobsons). À droite, cartes des différences
entre le jour et la nuit (jour - nuit, pour une échelle de -50 à +50 Dobsons). . . . 46
4.15 Les nuages de points correspondant à la comparaison entre EUMETSAT et le
LATMOS-ULB pour la journée du 1er septembre 2008 (JOUR) . . . . . . . . . 47
4.16 Les nuages de points correspondant à la comparaison entre EUMETSAT et le
LATMOS-ULB pour la journée du 1er septembre 2008 (NUIT). . . . . . . . . . 48
4.17 Couverture nuageuse en fonction du nombre de jours moyennés. Les différentes
courbes correspondent à différents jours de départ (1er août 2008, 15 août et 1er
septembre). Dès que la moyenne utilise plus de 5 jours, la fraction nuageuse
devient inférieure à 5% du globe. . . . . . . . . . . . . . . . . . . . . . . . . . 50
4.18 Histogrammes des valeurs sur un jour, 15 et 30, à partir du mois de septembre
2008. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
125](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-125-320.jpg)
![4.19 Dénombrement de l’écart relatif entre les données LATMOS-ULB avec le profil
de pression constant sur le globe et les données LATMOS-ULB avec le profil
de pression issu des données EUMETSAT, le tout sur 390 points (voir 4.6). Le
rouge correspond aux latitudes inférieures à 60˚S. . . . . . . . . . . . . . . . . 53
4.20 Pour deux points, observation du profil en [ppm] (courbe en haut à gauche), des
profils de pressions (suivant les calculs de la section précédente (voir l’équa-
tion 3.3) en noir, et l’équation 4.4 utilisée maintenant en rouge. Les résultats
donnent les profils d’ozone suivant avec un écart de +9% pour le point de gauche
[76.58,-91.67] et -53.46% pour le point de droite [-86.37,-156.08], situé en des-
sous de 60˚S. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
4.21 Comparaison sur cartes des valeurs du LATMOS-ULB avec l’ancienne méthode
à gauche, et la nouvelle à droite. Outre la réduction très importante du nombre
de points, on constate que la zone Antarctique est très inférieure à la première
version, et semble dorénavant bien mieux consistante avec la réalité du trou
dans la couche d’ozone. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
4.22 Comparaison sur cartes des valeurs du LATMOS-ULB avec l’ancienne méthode
en haut, et la nouvelle en bas. Ces cartes correspondent aux 10 premiers jours
du mois de septembre 2008. . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
4.23 Sur les journées des 31 août, 1er et 2nd septembre, nuages de points entre les
données LATMOS-ULB issues du premier calcul (L1) et du second calcul (L2). 55
4.24 Nuages de points entre les données d’EUMETSAT (en abscisse), et les données
du LATMOS-ULB (en ordonnées). La ligne du haut correspond à la première
version du LATMOS-ULB alors que celle du bas correspond à la méthode uti-
lisée dans cette section. On constate un net rapprochement des valeurs. Il s’agit
ici d’environ 450 points pour les journées du 31 août, 1er et 2nd septembre. . . . 56
4.25 Comparaison sur cartes des valeurs EUMETSAT (en haut) et LATMOS-ULB
(en bas). Ces cartes correspondent aux 10 premiers jours du mois de septembre
2008. Peu de points sont disponibles entre 30˚S et 60˚S, cependant, on observe
une bonne correspondance sur le globe. . . . . . . . . . . . . . . . . . . . . . 57
4.26 Distributions statistiques des valeurs EUMETSAT et LATMOS-ULB. À gauche,
différence entre les données EUMETSAT et LATMOS-ULB v2, avec une moyenne
à 11 Dobsons, soit +4%, au milieu, distribution statistique des valeurs entre ces
mêmes données et à droite, EUMETSAT corrigé selon son erreur estimée (voir
la section 4.4.4). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
4.27 Représentations des erreurs à partir du tableau 4.7. Sur la figure de gauche, en
rouge est représentée l’erreur du LATMOS-ULB en %, fonction de la colonne
d’ozone, en bleu est représentée l’erreur entre EUMETSAT et le LATMOS-
ULB et enfin, en noir, l’erreur totale en %. De cette erreur totale, on bâtit les
barres d’erreur sur le profil d’ozone, figure de droite. . . . . . . . . . . . . . . 60
4.28 Au 1er septembre 2008, distribution statistique des valeurs des colonnes totales
d’ozone en rouge pour MIPAS et en noir pour EUMETSAT. En bas, sur la
totalité des points, au milieu, lorsque la colonne partielle [0-18] est présente,
en haut, lorsque la colonne partielle [0-12] est présente. Le cas où la colonne
partielle [0-6] est présente n’a pas été représentée car elle comporte moins d’une
dizaine de points. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
4.29 Sélection sur une longitude de la colonne totale en fonction de la latitude. Figure
du haut, les valeurs sont prises telles quelles, alors que sur la figure du bas,
on ajoute aux données MIPAS les colonnes partielles [0-6] km d’EUMETSAT
correspondantes. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
126](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-126-320.jpg)
![4.30 Carte de la colonne totale d’ozone (DU) issue d’une journée de données MIPAS.
Le nombre de points est pour cette journée du 1er septembre 2008 est de 2318,
dont 35 disposent d’une colonne [0-6] km, 1257 d’une colonne [0-12] km et
2108 d’une colonne [0-18]km. . . . . . . . . . . . . . . . . . . . . . . . . . . 64
4.31 Distributions statistiques des valeurs de colonnes totales d’EUMETSAT issues
des produits de niveaux 2 (en noir) en comparaison avec la répartition sur grille
(en rouge). À gauche, sur une grille de 1.4˚×1.4˚et à droite, sur une grille de
2.8125˚×2.8125˚. Les valeurs sont en pourcentage du nombre total de points
valides (ie les points où il n’y a pas de données, -999, ont été omis). . . . . . . 65
4.32 Cartes Eumetsat non réparti sur une grille (en haut) et Eumetsat sur une grille
de 1.4˚×1.4˚ à gauche et 2.8125˚×2.8125˚ à droite. Afin d’observer au mieux
les similitudes, la grille graphique est identique pour les 3 cas et correspond à
la plus grande, c’est à dire celle de 2.8125˚. Les différences ne sont pas signifi-
catives. Il s’agit alors d’une réduction de finesse qui s’opère en agrandissant le
pas de la grille. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
5.1 Carte des données CNRM du 1er septembre 2008. On constate un grand fossé
au niveau des valeurs en dessous de -60˚de latitude. . . . . . . . . . . . . . . . 69
5.2 Distributions statistiques des valeurs en colonne totale d’ozone au 1er septembre
2008 pour les données d’EUMETSAT (en noir) sur grille et celles du CNRM
(en vert). À gauche est représenté la globalité des données, alors qu’à droite, une
sélection des latitudes supérieures à -60˚a été faite pour constater l’importance
de la zone Antarctique dans les données du CNRM (voir aussi 5.1). . . . . . . . 70
5.3 Colonne totale d’ozone au 1er septembre 2008 sur toutes les latitudes. En noir,
les valeurs d’EUMETSAT, en vert, les valeurs du CNRM, et en rouge, le pour-
centage de différence entre les deux (échelle à droite). . . . . . . . . . . . . . . 71
5.4 Représentation de la moyenne journalière des données d’EUMETSAT (noir),
d’EUMETSAT sur grille (noir, tirets), du LATMOS-ULB (rouge), de MIPAS
(bleu) et du CNRM (vert). . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
5.5 Carte orthographique ciblant le pôle Sud où la colonne totale d’ozone est très
inférieure à la limite de 220 Dobsons, en dessous de laquelle on considère qu’il
s’agit d’un trou dans la couche d’ozone. . . . . . . . . . . . . . . . . . . . . . 72
5.6 Colonne totale entre [-90˚,-60˚] en latitude et [-90˚,0˚] en longitude, ciblée sur
la zone Antarctique. Sont représentées en pointillés les moyennes avant et après
le 24 août, date d’apparition du trou de la couche d’ozone et les valeurs des
chutes. EUMETSAT chute de 14% alors que le CNRM chute de 46%. . . . . . 73
5.7 Distributions statistiques sur différents jours moyennés en grille de 1.4˚ pour
EUMETSAT et pour les données du CNRM. En haut à gauche : le 1er août
2008, en haut à droite, du 1er au 5 août, en bas à gauche, du 1er au 10 et en bas
à droite, du 1er au 31. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75
5.8 Colonne totale d’ozone pour tout le mois d’août 2008 sur toutes les latitudes.
En noir, les valeurs d’EUMETSAT, en vert, les valeurs du CNRM, et en rouge,
le pourcentage de différence entre les deux (échelle à droite). La moyenne de
ces pourcentages d’erreur est affichée (7.14798% pour 31 jours moyennés). . . 75
5.9 Déficit en millions de tonnes de l’ozone en dessous de 40˚S, relatif à 220 DU.
On observe bien l’apparition cyclique du trou au niveau des mois d’août, sep-
tembre, octobre et novembre de l’année. Crédit : NASA. . . . . . . . . . . . . 76
5.10 Distribution statistique sur 3 mois des données EUMETSAT et CNRM. Sur la
figure de gauche, les mois de Janvier, Février et Mars 2008, sur la figure de
droite, les mois d’Août, Septembre et Octobre 2008. . . . . . . . . . . . . . . . 77
127](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-127-320.jpg)
![5.11 Minimum, moyenne et maximum de la colonne totale issue des données CNRM
en dessous de 40˚S, sur toute l’année type. . . . . . . . . . . . . . . . . . . . . 77
5.12 On retrouve pour la colonne totale, entre 90˚S et 90˚N la distribution statistique
de la figure 5.10, à droite. Les valeurs sont résumées dans le tableau 5.4 pour
plus de lisibilité, avec les écarts relatifs exprimés. Malheureusement, pour des
raisons de capacité informatique de mémoire, ce graphique représente 2 mois :
janvier et février 2008. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
5.13 Minimum, moyenne et maximum de la colonne totale issue des données CNRM
en vert, EUMETSAT en noir, et EUMETSAT corrigé en rouge, le tout en des-
sous de 40˚S, sur toute l’année type et 2008. . . . . . . . . . . . . . . . . . . . 80
5.14 Carte du CNRM en représentation orthographique ciblée sur la zone Antarc-
tique afin de mettre en évidence le trou de la couche d’ozone et ses valeurs
extrêmement faible. Ici, l’échelle a été adaptée aux valeurs où 400 Dobsons
reste le maximum, mais le minimum devient 60 Dobsons. À droite, distribution
statistique des valeurs EUMETSAT et CNRM, à partir de 0 Dobson. . . . . . . 81
5.15 Carte des valeurs du CNRM, comprises entre 60 et 400 Dobsons (échelle étirée
par rapport aux précédentes cartes), pour la colonne totale, un 30 septembre. . 82
5.16 Carte des différences entre les points valides d’EUMETSAT et la carte du CNRM.
L’échelle est comprise entre -150 et +150 (c’est-à-dire le minimum et le maxi-
mum). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
6.1 Comparaison des minima, moyennes et maxima des différents jeux de données
avec en rouge, les données OMI fournies par la NASA, en noir, les données
EUMETSAT et en vert, les données du CNRM. À gauche, cas où les valeurs
d’EUMETSAT sélectionnées sont les latitudes inférieures à 60˚S et à droite,
inférieures à 40˚S. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85
6.2 Comparaison sur cartes des valeurs EUMETSAT, EUMETSAT "corrigées", LATMOS-
ULB et CNRM, correspondant aux 10 premiers jours du mois de septembre 2008. 86
6.3 Cartes centrées sur l’Antarctique pour 3 jours consécutifs : les 23, 24, 25 août
2008. La première ligne correspond aux cartes OMI, la seconde colonne cor-
respond aux cartes EUMETSAT. La gamme de couleur a été changée (table de
couleur IDL n˚33) pour correspondre à celle utilisée pour les cartes OMI de la
NASA. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
6.4 Pour les journées du 10 janvier, 10 février et 10 mars 2008, zoom sur les maxima
des valeurs en dessous de 60˚S (422, 490, et 534 DU). Les différences avec les
seconds maxima voisins (sur un carré de ±1˚) sont respectivement de 37, 84,
106 DU et 4, 77, 62 DU sur un carré de ±5˚. . . . . . . . . . . . . . . . . . . . 88
6.5 Aire, minimum et déficit en masse de l’ozone au dessus de l’Antarctique à partir
des données OMI de la NASA, avec un trio moyenne/maximum/minimum tiré
de l’ensemble des données 1979-2010, l’année 2010 en bleu et l’année 2011 en
rouge. Crédit : [33]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 90
6.6 Bandes spectrales IR et UV de l’ozone, avec le pic IR à 1100 cm-1 et les bandes
de Hartley et Huggins pour l’UV. Crédit : [34]. . . . . . . . . . . . . . . . . . 92
6.7 Spectres en radiance au-dessus de l’Antarctique. En bleu, au-dessus de l’océan,
proche de l’Antarctique, en rouge, au-dessus du continent. Crédit : [41]. . . . . 94
128](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-128-320.jpg)

![Liste des tableaux
1.1 Caractéristiques du satellite MetOp . . . . . . . . . . . . . . . . . . . . . . . . 7
2.1 Résolution requise pour des observations du profil de l’ozone basée au nadir
(cas IASI) en considérant que la tropopause s’établit là où l’ozone atteint une
concentration de 150 ppbv, que l’UTLS s’étend de 5 à 25 km, et qu’enfin, l’at-
mosphère moyenne s’étend quant à elle de 25 à 80 km d’altitude ([25]). Les
objectifs scientifiques de ces observations sont de décrire les différences ré-
gionales de l’évolution de la couche d’ozone, de mettre en évidence les cycles
saisonniers, la variabilité interannuelle et à court terme, de caractériser le poids
de l’ozone troposphérique et enfin d’en tirer les tendances globales. . . . . . . 20
3.1 Format des données IASI fournies par le LATMOS-ULB. Chaque ligne corres-
pond à un point. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
3.2 Format des données MIPAS provenant de l’IMK. Chaque point de l’espace aura
ces 8 colonnes et ∼60 lignes. Latitude et longitude se récupèrent en en-tête des
colonnes (voir annexe D). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
4.1 Méthode d’échantillonnage spatial. . . . . . . . . . . . . . . . . . . . . . . . . 31
4.2 Statistiques suivant l’altitude de la tropopause ht mathématique pour le 1er sep-
tembre 2009. Sont regroupés ici la moyenne x, l’écart-type σ, et le nombre de
¯
points utilisés. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
4.3 Coefficients de corrélations, coefficients directeurs et ordonnées à l’origine as-
sociés aux nuages de points de la figure 4.9, pour le 1er septembre 2008. On
distingue assez facilement les valeurs où la corrélation est faible (loin des lati-
tudes moyennes). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
4.4 Colonnes partielles et totale (en DU) du 1er septembre 2008 (en noir, EUMET-
SAT et en rouge, LATMOS-ULB) et leurs séparations en données jour et nuit. . 46
4.5 Coefficients de corrélations, coefficients directeurs et ordonnées à l’origine as-
sociés aux nuages de points de la figure 4.15 et 4.16, pour le 1er septembre
2008, séparé en données jour (noir) et données nuit (bleu). On distingue assez
facilement les valeurs où la corrélation est faible (loin des latitudes moyennes). 49
4.6 Tableau regroupant les coefficients directeurs, ordonnées à l’origine, coeffi-
cients de corrélation et nombres de points correspondant aux nuages de points
entre les données d’EUMETSAT et les nouvelles données LATMOS-ULB sur
différents jours. C’est à partir de ces valeurs qu’est calculée l’erreur d’EUMET-
SAT. La moyenne est basée sur toutes les valeurs disponibles, c’est à dire du 15
août 2008 au 30 septembre (21 et 27 août exclus par manque de valeurs). . . . . 58
130](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-130-320.jpg)
![4.7 Erreur estimée d’EUMETSAT à partir de l’erreur observée avec les données
LATMOS-ULB. La deuxième colonne correspond à l’erreur des données LATMOS-
ULB, la troisième colonne correspond à l’erreur des données EUMETSAT par
rapport aux données LATMOS-ULB, la quatrième colonne correspond à l’équa-
tion 4.5, c’est-à-dire l’erreur totale, et la cinquième colonne correspond à l’er-
reur totale relative. (* : l’absence de valeur entre 95 et 105 Dobsons explique le
Not a Number, qui sera assimilé à la valeur moyenne pour le calcul de l’erreur). 61
4.8 Écarts sur les moyennes totales des colonnes totales sur les 2 mois d’août et
septembre 2008. À gauche, sélection de tous les points, ensuite, sélection où [0-
18] km = 0, sélection où [0-12] km = 0 et enfin sélection où [0-6] km = 0. Seuls
les jours communs entre EUMETSAT et MIPAS ont été sélectionnés (absence
de 3 jours par mois environ). La dernière moyenne d’EUMETSAT diffère car
certains jours de MIPAS ne disposent pas de la colonne [0-6] km. . . . . . . . . 64
4.9 Sur la journée du 1er septembre 2008, valeurs des colonnes partielles et totales
d’ozone suivant la répartition ou non sur grille, de 1.4˚×1.4˚et 2.8125˚×2.8125˚. 66
5.1 Sur la journée du 1er septembre 2008, valeurs des colonnes partielles et totales
d’ozone suivant la répartition ou non sur grille, de 1.4˚×1.4˚et 2.8125˚×2.8125˚.
En noir, les valeurs correspondant à la totalité du globe. En rouge, uniquement
les latitudes supérieures à -60˚. . . . . . . . . . . . . . . . . . . . . . . . . . . 70
5.2 Variations entre les moyennes d’EUMETSAT et du CNRM en pourcentage sur
une journée, 5, 10, 15, 25 et 31, soit tout le mois d’août 2008. Puis même chose
sur tout le mois de septembre de la même année. . . . . . . . . . . . . . . . . . 74
5.3 Même tableau que 5.2, mais avec les hautes latitudes (<-60˚) ôtées. . . . . . . . 74
5.4 En unité Dobson, tableau regroupant les valeurs des moyennes d’EUMETSAT
et du CNRM sur différentes latitudes et pour les colonnes partielles/totale, sur
les mois de janvier, février et mars 2008, puis d’août, septembre et octobre de
la même année. La première partie correspond à la figure 5.12. . . . . . . . . . 78
5.5 Sur la journée du 30 septembre 2008, tableau des moyennes et écarts-types des
différentes colonnes pour EUMETSAT et le CNRM (en Dobsons). . . . . . . . 81
C.1 IASI spectral band and possible information available. . . . . . . . . . . . . . 104
C.2 Level-2 quality of ozone from IASI . . . . . . . . . . . . . . . . . . . . . . . 105
C.3 Generalities about the IASI instrument. . . . . . . . . . . . . . . . . . . . . . 107
E.1 Volume de données traitées suivant les différentes origines (le tout en Mo) et
le total (en Go). Ainsi, un mois de données correspond à plus de 309 Go de
données. Si on ne prend que les données d’EUMETSAT pour la routine, on
arrive à un total de 342 Go. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122
131](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-131-320.jpg)
![Bibliographie
[1] http://www.cnes.fr/
[2] http://www.esa.int/esaME/index.html
[3] Clerbaux C., Boynard A., Clarisse L., George M., Hadji-Lazaro J., Herbin H., Hurtmans
D., Pommier M., Razavi A., Turquety S., Wespes C., and Coheur P.-F., Monitoring of atmos-
pheric composition using the thermal infrared IASI/MetOp Sounder, Atmos. Chem. Phys., 9,
6041-6054, 2009.
http://www.atmos-chem-phys.net/9/6041/2009/
[4] GIEC, Bilan 2007 des changements climatiques. Contribution des Groupes de travail I,
II et III au quatrième Rapport d’évaluation du Groupe d’experts Intergouvernemental sur
l’évolution du Climat, 2007, [équipe de rédaction principale, Pachauri, R.K. et Reisinger,
A.]. GIEC, Genève, Suisse, ..., 103 pages.
[5] World Meteorological Organization (WMO)/United Nations Environment Programme
(UNEP), 2007. Scientific Assessment of Ozone Depletion : 2006, WMO, Global Ozone Re-
search and Monitoring Project, Report No. 50, Geneva, Switzerland.
[6] IPCC, 2007 : Climate Change 2007 : The Physical Science Basis. Contribution of Working
Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change
[Solomon S., Qin D., Maning M., Chen Z., Marquis M., Averyt K.B., Tignor M., and Miller
H.L.]. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA,
996pp.
[7] Waugh D.L., Oman L., Kawa S.R., Stolarski R.S., Pawson S., Douglass A.R., Newman
P.A., and Nielsen J.E., Impacts of climate change on stratospheric ozone recovery, Geophys.
Res., Lett, 2009, 39, doi :10.1029/2008GL036223.
[8] http://www.pa.op.dlr/de/CCMVal/
[9] Eyring V., Shepherd T.G., Waugh D.W., SPARC Report on the Evaluation of Chemistry-
Climate Models, June 2010 .
[10] Austin J., Wilson R.J., Ensemble simulations of the decline and recovery of stratospheric
ozone, J. Geophys. Res., 2006, 111, doi : 10.1029/2005JD006907.
[11] Lamarque J.-F., Kinnison D.E., Hess P.G., and Vitt F.M., Simulated lower stratospheric
trends between 1970 and 2005 : Identifying the role of climate and composition changes,
2008, J. Geophys. Res., 113, doi :10.1029/2007JD009277.
[12] Scinocca J.-F., McFarlane N.A., Lazare M., Li J. and Plummer D., Technical note : The
CCCma third generation AGCM and its extension ino the middle atmosphere, 2008, Atmos.
Chem. Phys., 8, 7055-7074.
[13] Déqué M., Frequency of precipitation and temperature extremes over France in an an-
thropogenic scenario : model results and statistical correction according to observed values,
2007, Global and Planetary Change, 57, 16-26.
[14] Stenke A., Grewe V. and M. Ponater, Lagrangian transport of water vapor and cloud
water in the ECHAM4 GCM and its impact on the cold bias, 2008a, Clim Dyn., 31, 491-506
132](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-132-320.jpg)
![[15] Jöckel P., Tost H., Pozzer A., Brühl C., Buchholz J., Ganzeveld L., Hoor P. Kerkweg A.,
Lawrence M.G., Sander R., Steil B., Stiller G., Tanarhte M., Taraborelli D., van Aardenne J.
and Lelieveld J., The atmospheric chemistry general circulation model ECHAM5/MESSy1 :
Consistent simulation of ozone from the surface to the mesosphere, Atmos. Chem. Phys., 6,
5067-5104.
[16] Roeckner E., and Coauthors, The atmospheric general circulation model ECHAM5. Part
I : Model description, 2003, Rep. 349, Max-Planck-Institut fuer Meteorologie, Hamburg,
Germany, 5-6.
http://www.mpimet.mpg.de.
[17] Rienecker M. M., et al., The GOES-5 Data Assimilation System - Documentation of ver-
sions 5.0.1, 5.1.0, and 5.2.0, NASA/TM-2008-104606, Vol. 27, Tech. Rep. Series on Global
Modeling and Data Assimilation, 118 pp.
http://gmao.gsfc.nasa.gov/systems/goes5/
[18] Jourdain L., Bekki S., Lott F. and Lefèvre F., The coupled chemistry-climate model LMDz-
REPRO-BUS : description and evaluation of a transient simulation of the period 1980-1999,
Ann. Geophys., 26, 1391-1413.
[19] Shibata K. and Deushi M., Long-term variations and trends in the simulation of the middle
atmosphere 1980-2004 by the chemistry-climate model of the Meteorological Research Ins-
titute, 2008a, Ann. Geophys., 26, 1299-1326.
[20] Egorova T., Rozanov E., Zubov V., Manzini E., Schmutz W. and Peter T., Chemistry-
Climate model SOCOL : a validation of the present-day climatology, 2005, Atm. Chem.
Phys., 5, 1557-1576.
[21] Morgenstern O., Braesicke P., O’Connor F.M., Bushell A.C., Johnson C.E., Osprey S.M.,
and Pyle J.A., Evaluation of the new UKCA climate-composition-model. Part 1 : The stra-
tosphere, 2009, Geosci. Model Dev., 1, 43-57.
[22] http://www.cesm.ucar.edu/working_groups/WACCM/
[23] http://dss.ucar.edu/datasets/common/ecmwf/ERA40/docs/
horizontal-coordinate/index.html
[24] http://www.ecmwf.int/products/data/technical/gaussian/
index.html
[25] http://www.esa-ozone-cci.org/
[26] Manual of the ICAO standard atmosphere calculations by the NACA. (Author(s) Not
Available) naca-tn-3182. May 1954.
http://naca.central.cranfield.ac.uk/reports/1954/
naca-tn-3182.pdf
[27] Saunois M., Emmons L., Lamarque J.-F. and Thouret V., Relationship between the North
Atlantic Oscillation and the inter annual variability of ozone and other trace gases : a data
analysis and modeling study, P-Chemistry Climate.46 ID :4195 15 :35
[28] http://sacs.aeronomie.be/info/sza.php
[29] Schwartz S.E., Warneck P., Units for use in atmospheric chemistry, 1995, PAC 67 1377-
1406.
[30] http://www.cci-cmug.org/
[31] http://www.unidata.ucar.edu/software/netcdf/
[32] Rodgers C.D., Inverse Methods for Atmospheric Sounding : Theory and Practice, World
Scientific Publishing Co. Ltd., 2000.
133](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-133-320.jpg)
![[33] http://ozonewatch.gsfc.nasa.gov/
[34] Gratien A., PuD Thesis, University Paris 12 - Val de Marne, Spectroscopie ultraviolet-
visible et infrarouge de molécules clés atmosphériques, Picquet-Varrault B. and Orphal J.,
2008.
[35] Smith M. A. H., Malathy Devi V., Chris Benner D. and Rinsland C. P., Absolute intensities
of O3 in the 9-11 µm region, 2001, Journal of Geophysical Research, 106 :9909-9921.
[36] Schneider M., Redondas A., Hase F., Guirado C., Blumenstock T. and Cuevas E., Compa-
rison of ground-based Brewer and FTIR total O3 monitoring techniques, 2008, Atmospheric
Chemistry and Physics Discussions 8 :285-325.
[37] Yamamori M., Kagawa A., Kasai Y., Mizutani K., Murayama Y., Sugita T., Irie H. and
Nakajima H., Validation of ILAS-II version 1.4 O3 , HN O3 , and temperature data through
comparison with ozonesonde, groud-based FTS, and lidar measurements in Alaska, 2006,
Journal of Geophysical Research - Atmospheres 111 (D11).
[38] Siddans R., Latter B., Poulsen C. and Kerridge B., New Developments in the Retrieval
of Tropospheric Ozone from GOME, SCIAMACHY and SEVIRI, 2006, ESA Atmospheric
Science Conference, Frascati, Italie.
[39] Picquet-Varrault B., Orphal J., Doussin J.F., Carlier P. and Flaud J.-M., Laboratory Inter-
comparison of the ozone absorption coefficients in the mid-infrared (10 µm) and ultraviolet
(300-350 nm) spectral regions, 2005, Journal of Physical Chemistry A109(6) : 1008-1014.
[40] Turquety S., PhD Thesis, University Paris 6 - Pierre et Marie Curie, Mesure de l’ozone tro-
posphérique à partir d’observations satellitaires dans le domaine de l’infrarouge, Advisors :
Clerbaux C. and Mégie G., 2006.
[41] Scannell C., Hurtmans D., Boynard A., Hadji-Lazaro J., George M., Delcloo A., Tuinder
O., Coheur P.-F., Clerbaux C., A review of the ozone hole from 2008 to 2010 as observed by
IASI, Atmospheric Measurement Techniques Discussions 4, 4 (2011) 4717-4752
[42] Rodgers C.D., and Connor B.J., Intercomparison of remote sounding instruments, J. Geo-
phys. Res., 108(D3), 4116, doi :10.1029/2002JD002299, 2003.
[43] Eremenko M., Dufour G., Foret G., Keim C., Orphal J., Beekmann M., Bergametti G.,
and J.-M. Flaud, 2008, Tropospheric ozone distributions over Europe during the heat wave
in July 2007 observed from infrared nadir spectra recorded by IASI, Geophys. Res. Lett., 35,
L18805, doi :10.1029/2008GL034803.
[44] Boynard A., Clerbaux C., Coheur P.-F., Hurtmans D., Turquety S., George M., Hadji-
Lazaro J., Keim C. and J. Meyer-Arnek J., Measurements of total and tropospheric ozone
from IASI : comparison with correlative satellite, ground-based and ozonesonde observa-
tions, Atmos. Chem. Phys., 9, 6255-6271, 2009.
http://www.atmos-chem-phys.net/9/6255/2009/
http://www.lmd.polytechnique.fr/~Esturquet/these_turquety.
pdf.gz
[45] Keim C., Eremenko M., Orphal J., Dufour G., Flaud J.-M., Höpfner M., Boynard A.,
Clerbaux C., Payan S., Coheur P.-F., Hurtmans D., Claude H., Dier H., Johnson B., Kelder
H., Kivi R., Koide T., Lòpez Bartolomé M., Lambkin K., Moore D., Schmidlin F. J., and
Stübi R., Tropospheric ozone from IASI : comparison of different inversion algorithms and
validation with ozone sondes in the northern middle latitudes, Atmos. Chem. Phys. Discuss.,
9, 11441-11479, 2009,
http://www.atmos-chem-phys-discuss.net/9/11441/2009/
[46] EUMETSAT : IASI Level 1 Product Guide, EUM/OPS-EPS/MAN/04/0032. v3F, 6
December 2010
134](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-134-320.jpg)
![http://oiswww.eumetsat.org/WEBOPS/eps-pg/IASI-L1/
IASIL1-PG-index.htm
[47] EUMETSAT : IASI Level 2 Product Guide, EUM/OPS-EPS/MAN/04/0033. v2E, 25
March 2011
http://oiswww.eumetsat.org/WEBOPS/eps-pg/IASI-L2/
IASIL2-PG-0TOC.htm
[48] http://www.eumetsat.int/Home/Main/DataProducts/index.htm
135](https://image.slidesharecdn.com/rapport-111004135628-phpapp02/85/Rapport-de-stage-135-320.jpg)