Téléchargé parFootballLovers9
TS-TC-Statistique-presentation.pdf
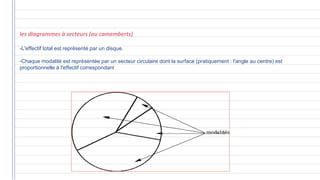
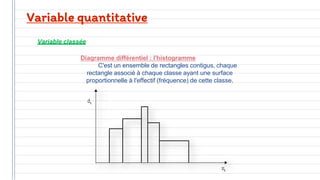
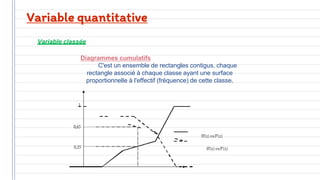
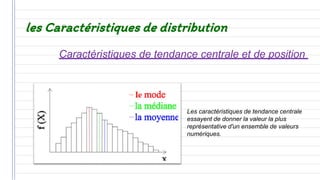
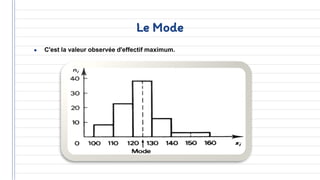
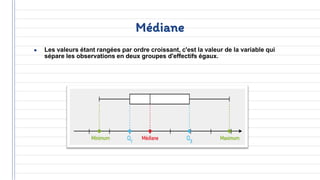
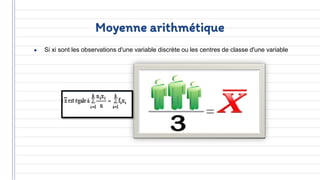
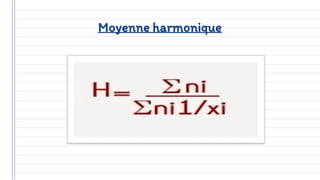
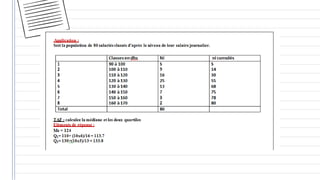
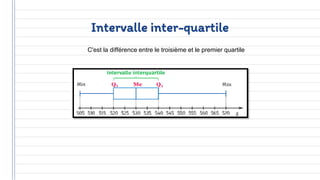
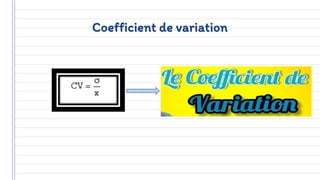
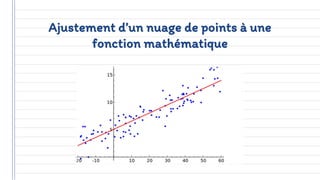
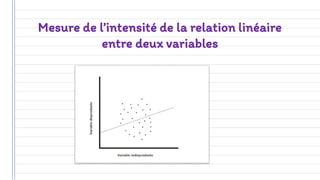
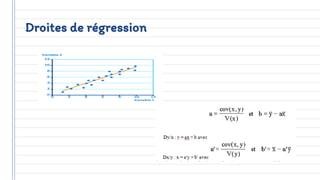
Ce document traite des concepts fondamentaux de la statistique, incluant les variables qualitatives et quantitatives, ainsi que les représentations graphiques. Il aborde également les caractéristiques de distribution, telles que les tendances centrales, les caractéristiques de dispersion, et les méthodes de régression et de corrélation. En résumé, la statistique est présentée comme un outil essentiel pour l'analyse et la description des données économiques.
![Statistiques descriptives [PDF].pptx](https://cdn.slidesharecdn.com/ss_thumbnails/statistiquesdescriptivespdf-230610144146-996f5931-thumbnail.jpg?width=640&height=640&fit=bounds)
![Statistiques descriptives [PDF].pptx](https://cdn.slidesharecdn.com/ss_thumbnails/statistiquesdescriptivespdf-230610140034-d4876a87-thumbnail.jpg?width=640&height=640&fit=bounds)
TS-TC-Statistique-presentation.pdf
- 2.
- 3. Plan ● Statistique ● Généralités ●Qualification d’une variable qualitative et variable quantitative ● Représentations graphiques ● les Caractéristiques de distribution ● Régression et corrélation
- 5. Généralités statistique : méthodescientifique qui vise à observer, collecter, analyser des données quantitatives. La statistique descriptive est la partie de la statistique qui sert à décrire un phénomène Définitions :
- 6. Apport de lastatistique aux économistes La statistique est utile aux praticiens de l’économie La statistique est utile aux théoriciens Apport de la statistique aux économistes
- 7. Pour une variablequalitative, les modalités ne sont pas mesurables. Pour une variable quantitative, les modalités sont mesurables. Ce sont : • des valeurs numériques ponctuelles lorsque la variable est discrète • des intervalles lorsque la variable est continue ou lorsque la variable est discrète et qu'elle comporte beaucoup de modalités Qualification d’une variable qualitative et variable quantitative
- 8.
- 9. Variable qualitative : Lestuyaux d'orgue (ou diagramme en barre ou diagramme à bandes
- 10. les diagrammes àsecteurs (ou camemberts) -L'effectif total est représenté par un disque. -Chaque modalité est représentée par un secteur circulaire dont la surface (pratiquement : l'angle au centre) est proportionnelle à l'effectif correspondant
- 11.
- 13. Variable quantitative Variable discrète Diagrammedifférentiel : le diagramme en bâtons Les valeurs discrètes xi prises par les variables sont placées sur l'axe des abscisses, et les effectifs (ou les fréquences) sur l'axe des ordonnées. La hauteur du bâton est proportionnelle à l'effectif.
- 14. Variable quantitative Variable discrète Diagrammescumulatifs : ils permettent de visualiser l'évolution des effectifs (fréquences) cumulés croissants ou décroissants.
- 15. Variable quantitative Variable classée Diagrammedifférentiel : l'histogramme C'est un ensemble de rectangles contigus, chaque rectangle associé à chaque classe ayant une surface proportionnelle à l'effectif (fréquence) de cette classe.
- 16. Variable quantitative Variable classée Diagrammescumulatifs C'est un ensemble de rectangles contigus, chaque rectangle associé à chaque classe ayant une surface proportionnelle à l'effectif (fréquence) de cette classe. .
- 17.
- 19. les Caractéristiques dedistribution Caractéristiques de tendance centrale et de position Les caractéristiques de tendance centrale essayent de donner la valeur la plus représentative d'un ensemble de valeurs numériques.
- 20. Le Mode ● C'estla valeur observée d'effectif maximum.
- 21.
- 23. Médiane ● Les valeursétant rangées par ordre croissant, c'est la valeur de la variable qui sépare les observations en deux groupes d'effectifs égaux.
- 24.
- 26. Moyenne arithmétique ● Sixi sont les observations d'une variable discrète ou les centres de classe d'une variable
- 27.
- 29.
- 30.
- 31.
- 33. Moyenne quadratique Si xisont les observations d'une variable quantitative, la moyenne harmonique est égale à
- 34. Quartiles Ce sont descaractéristiques de position. Les quartiles sont obtenus lorsqu'on a cumulé 25, 50, 75% de la population Les déciles sont obtenus lorsqu'on a cumulé 10, 20,. , 90% de la population Les centiles sont obtenus lorsqu'on a cumulé 1, 2,. , 99% de la population
- 35.
- 37. les Caractéristiques dedistribution Caractéristiques de dispersion Comme leur nom l'indique, ces caractéristiques essayent de synthétiser par une seule valeur numérique la dispersion de toutes les valeurs observées.
- 38. Étendue C'est la différenceentre la plus grande et la plus petite observation
- 39.
- 41. Intervalle inter-quartile C'est ladifférence entre le troisième et le premier quartile
- 42.
- 44.
- 45.
- 46.
- 48. Lorsqu'on observe deuxvariables quantitatives sur les mêmes individus, on peut s'intéresser à une liaison éventuelle entre ces deux variables. La régression fournit une expression de cette liaison sous la forme d'une fonction mathématique. La corrélation renseigne sur l'intensité de cette liaison. Régression et corrélation
- 49. Ajustement d’un nuagede points à une fonction mathématique
- 50. Ajustement linéaire parla méthode des moindres carrés ● Lorsque le nuage de points (xi , yi) est à peu près rectiligne, on peut envisager d'exprimer la liaison entre x et y sous forme de fonction affine y = ax + b
- 51. Mesure de l’intensitéde la relation linéaire entre deux variables
- 52.
- 53.
- 54.