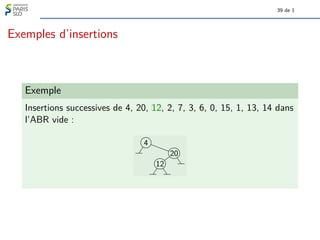
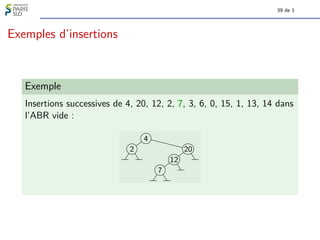
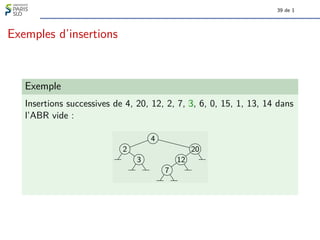
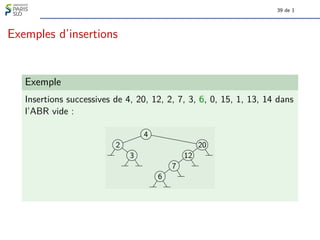
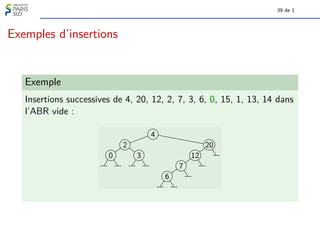
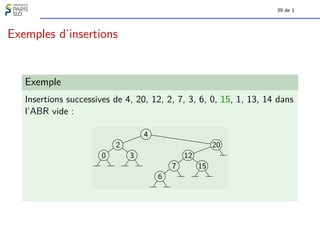
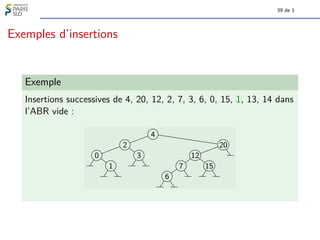
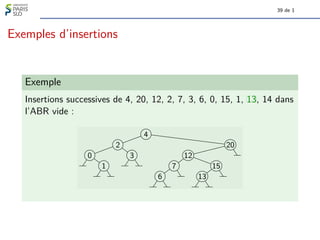
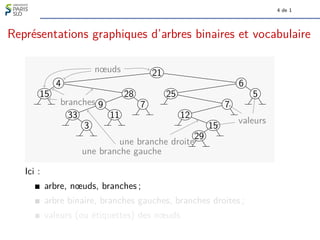
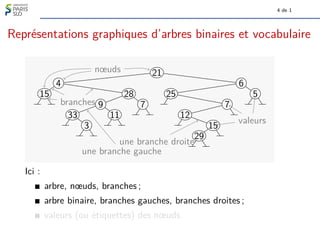
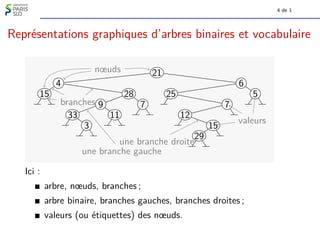
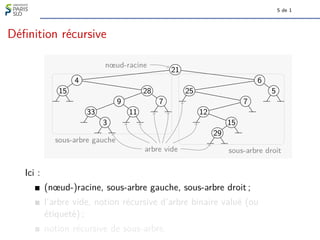
Le document traite des algorithmes et structures de données, se concentrant sur les arbres binaires, leur définition, leurs types (comme les arbres binaires de recherche et les arbres-tournoi), et leur représentation graphique. Il aborde également des concepts associés tels que la taille et la hauteur des arbres ainsi que les algorithmes liés à la génération et à la classification des arbres. Enfin, il explore des notions comme le nombre de Catalan qui determine le nombre d'arbres binaires avec un certain nombre de nœuds.

















![24 de 1
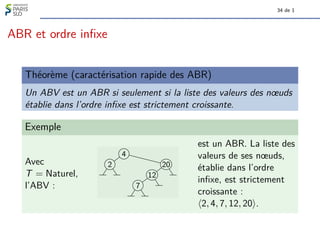
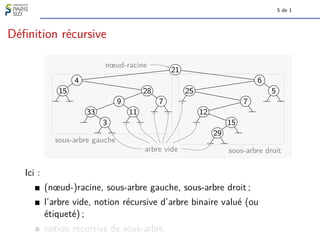
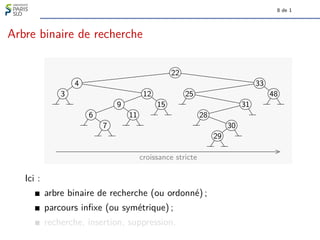
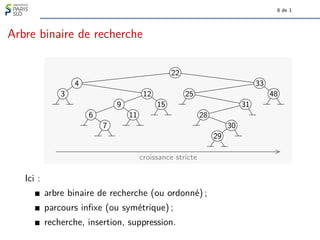
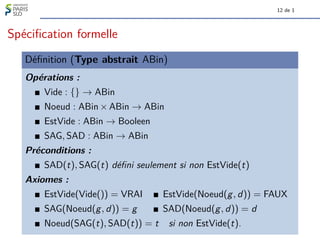
Définition
Soit (a, hb1, b2, . . . , bki) le chemin menant de a à a0.
Le numéro de a0 relativement à a, noté Numa(a0), est
[1b1b2 . . . bk]2, l’entier dont l’écriture en base 2 est 1 b1 b2 . . . bk.
Autrement dit :
racine : 1 ;
vers la gauche : ×2, +0 ;
vers la droite : ×2, +1.
below:8
15
above:4
below:9
4
above:2
below:40
33
above:20
below:82
3
above:41
below:83
9
above:10
below:42
11
above:21
below:43
28
above:5
below:22
7
above:11
below:23
21
above:1
below:12
25
above:6
below:52
12
above:26
below:212
29
above:106
below:213
15
above:53
below:107
7
above:13
below:27
6
above:3
below:14
5
above:7
below:15](https://image.slidesharecdn.com/06-arbres-211117233547/85/06-arbres-39-320.jpg)
![24 de 1
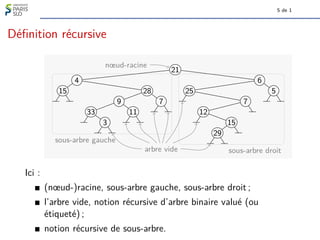
Définition
Soit (a, hb1, b2, . . . , bki) le chemin menant de a à a0.
Le numéro de a0 relativement à a, noté Numa(a0), est
[1b1b2 . . . bk]2, l’entier dont l’écriture en base 2 est 1 b1 b2 . . . bk.
Autrement dit :
racine : 1 ;
vers la gauche : ×2, +0 ;
vers la droite : ×2, +1.
below:8
15
above:4
below:9
4
above:2
below:40
33
above:20
below:82
3
above:41
below:83
9
above:10
below:42
11
above:21
below:43
28
above:5
below:22
7
above:11
below:23
21
above:1
below:12
25
above:6
below:52
12
above:26
below:212
29
above:106
below:213
15
above:53
below:107
7
above:13
below:27
6
above:3
below:14
5
above:7
below:15](https://image.slidesharecdn.com/06-arbres-211117233547/85/06-arbres-40-320.jpg)
![24 de 1
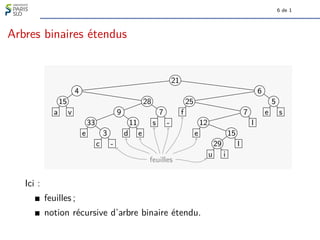
Définition
Soit (a, hb1, b2, . . . , bki) le chemin menant de a à a0.
Le numéro de a0 relativement à a, noté Numa(a0), est
[1b1b2 . . . bk]2, l’entier dont l’écriture en base 2 est 1 b1 b2 . . . bk.
Autrement dit :
racine : 1 ;
vers la gauche : ×2, +0 ;
vers la droite : ×2, +1.
below:8
15
above:4
below:9
4
above:2
below:40
33
above:20
below:82
3
above:41
below:83
9
above:10
below:42
11
above:21
below:43
28
above:5
below:22
7
above:11
below:23
21
above:1
below:12
25
above:6
below:52
12
above:26
below:212
29
above:106
below:213
15
above:53
below:107
7
above:13
below:27
6
above:3
below:14
5
above:7
below:15](https://image.slidesharecdn.com/06-arbres-211117233547/85/06-arbres-41-320.jpg)