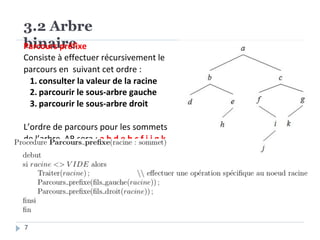
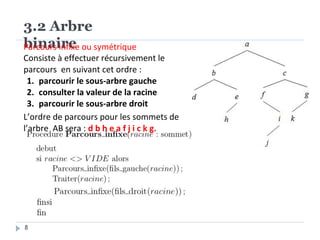
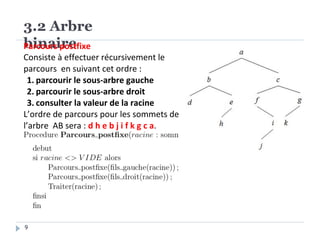
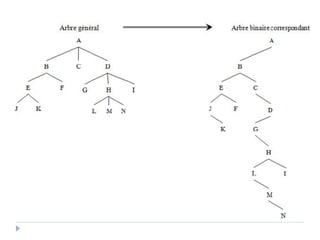
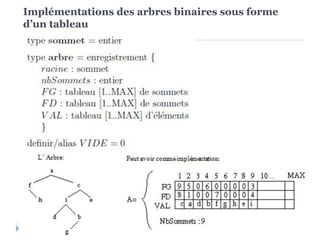
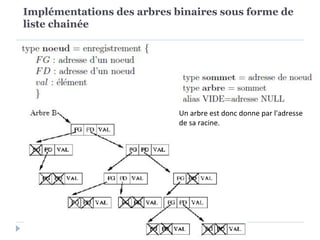
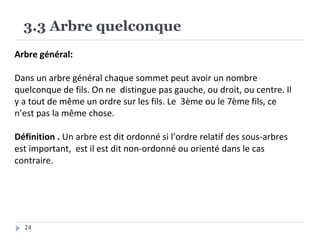
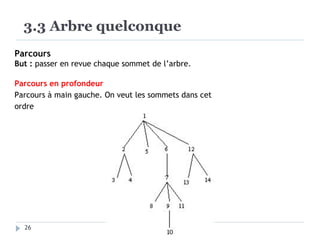
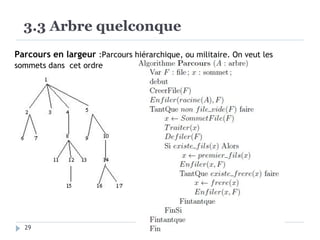
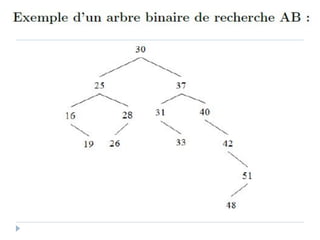
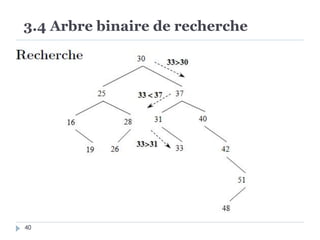
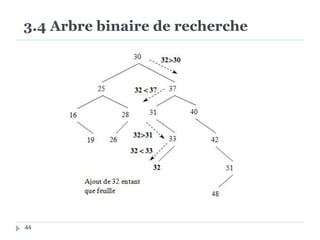
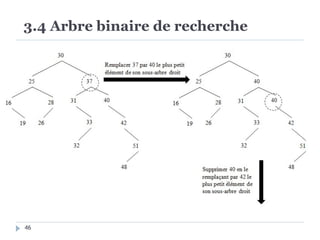
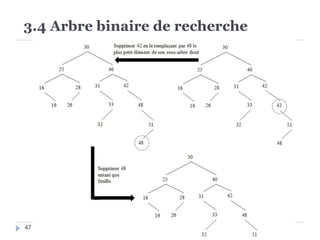
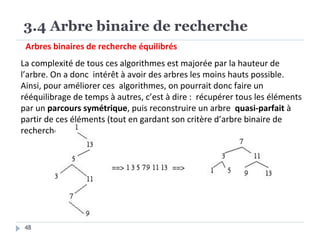
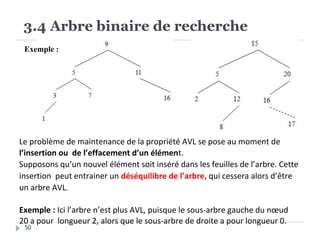
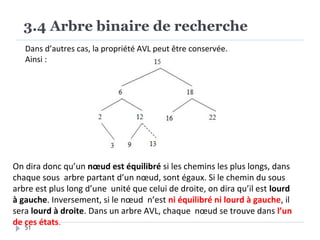
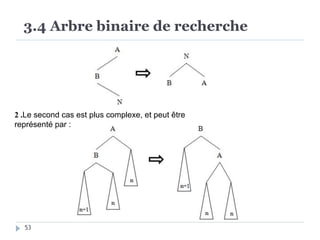
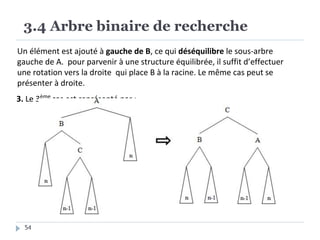
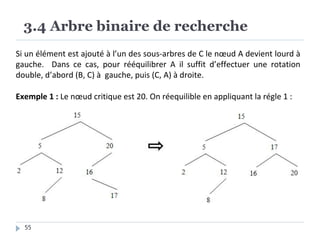
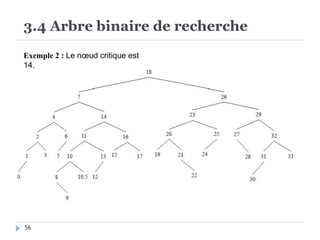
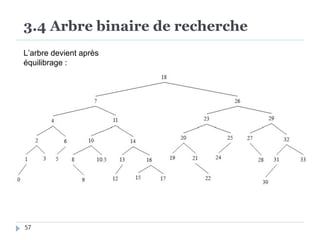
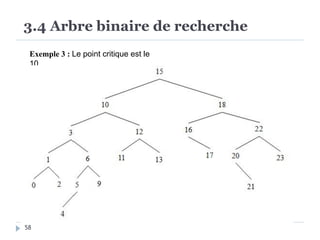
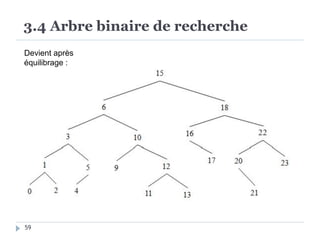
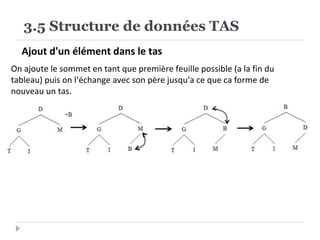
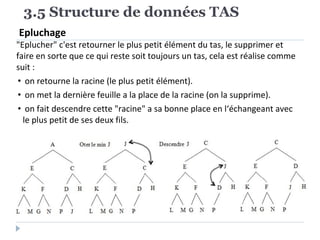
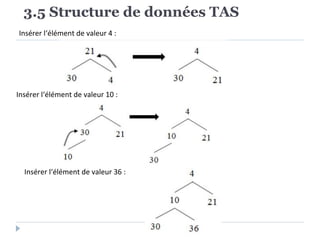
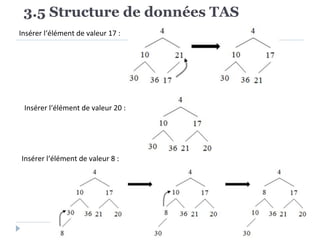
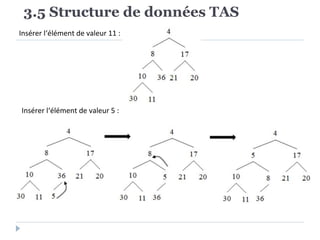
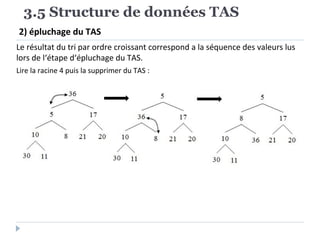
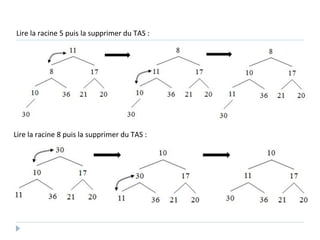
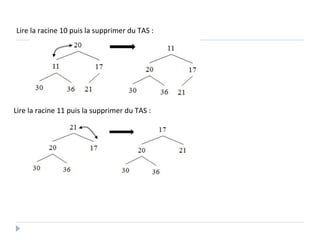
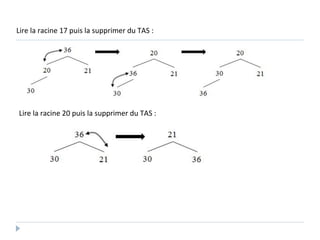
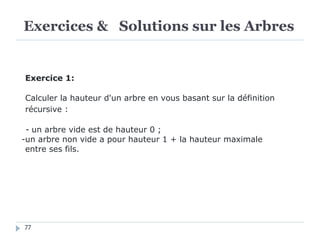
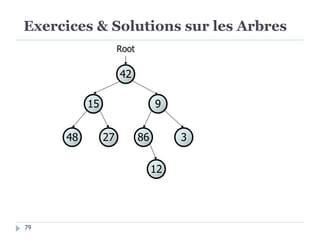
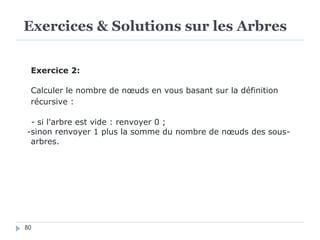
Le document présente les structures d'arbres en informatique, en se concentrant particulièrement sur les arbres binaires et leurs variants. Il décrit les définitions, les propriétés, les primitives de manipulation, et les méthodes de parcours des arbres. De plus, il aborde les arbres binaires de recherche et leur importance pour la recherche efficace des éléments, tout en discutant des techniques d'équilibrage pour optimiser leurs performances.

1. Les Arbres
Dr BEN-NAOUM Farah
1
Université Djillali liabes
Département d‘Informatique
Chapitre 3

2. 3.1 Présentation
2
• Une structure en arborescence est une série d’éléments placés
hiérarchiquement à fin qu’un élément puisse avoir un ou plusieurs
éléments en dessus. On appelle aussi arbre un ensemble d’
éléments (appelé nœuds) dont on distingue :
- La racine dont sont issus tous les autres nœuds.
- Les autres nœuds appelés fils ou descendants de la racine.
• La structure d’arbre est l’une des plus importantes et des plus
spécifiques de l’informatique. Par exemple : organisation des fichiers
dans les systèmes d’exploitation, représentation des programmes
traités par un ordinateur, d’une table des matières, d’un
questionnaire, d’un arbre généalogique, ect. C’est une structure de
données qui permet d’écrire des algorithmes très performants.
• Nous verrons tout d’abord les arbres binaires, qui sont un cas
particulier des arbres généraux. Une propriété intrinsèque de cette
structure est la récursivité.

3. 3.2 Arbre
binaire
Définitions
Soit un ensemble de sommets (ou encore noeuds) auxquels sont
associés des ”valeurs” (les éléments à stocker : entier, chaîne,
structure, ...). Un arbre binaire est défini récursivement de la manière
suivante :
• soit d’un seul sommet appelé racine,
• soit d’un sommet racine à la gauche duquel est accroché un sous-arbre
binaire gauche
• soit d’un sommet racine à la droite duquel est accroché un sous-arbre
binaire droit
• soit d’un sommet racine auquel sont accrochés un sous-arbre
binaire droit et un sous- arbre binaire gauche
3

4. 3.2 Arbre
binaire
4
Définition 1:
• fils gauche de x = le sommet (s’il existe) accroché à la gauche de x.
• fils droit de x = le sommet (s’il existe) accroché à la droite de x.
• fils de x = le ou les deux sommets accrochés sous x.
• Père de x=le sommet p tel que x est fils de p.
• frère de x = un sommet (s’il existe) qui a le même père.
• sommet interne = un sommet qui a au moins un fils (gauche ou droit ou
les deux).
• feuille = un sommet qui n’a pas de fils.
• branche = un chemin de fils en fils de la racine vers une feuille.
• branche gauche = la branche de fils gauche en fils gauche.
• branche droite = la branche de fils droit en fils droit.
• hauteur d’un sommet x = la longueur (en nombre d’arcs) du plus long
chemin de x à une feuille.
• hauteur d’un arbre = la hauteur de la racine.
• profondeur d’un sommet x = la longueur (en nombre d’arcs) du
chemin de la racine au sommet.

5. 3.2 Arbre
binaire
5
Primitives de consultation
– racine( B : arbre) :sommet ; retourne la racine de l’arbre.
– fils gauche(x : sommet, B : arbre) : sommet ; retourne le sommet fils
gauche de x ou VIDE.
– fils droit(x : sommet, B : arbre) : sommet ; retourne le sommet fils droit de
x ou VIDE.
– père(x : sommet, B : arbre) : sommet ; retourne le sommet père de x ou
VIDE.
– val(x : sommet, B :arbre) :élément ; retourne l’élément stocké au sommet
x.
– vide(B : arbre) : booleen ; retourne vrai ou faux.
Primitives de construction/modifications
– créer arbre vide() : arbre ; création d’un arbre initialisé comme il faut.
– créer sommet(e :élément, B : arbre) : sommet ; retourne le sommet.
– faire FG(père : sommet , fg : sommet, B : arbre) retourne l’arbre
– faire FD(père : sommet, fd : sommet, B : arbre) retourne l’arbre

6. 3.2 Arbre
binaire
6
Parcours
But : passer en revue (pour un traitement quelconque) chaque
sommet une et une seule fois.
Théorème 2. Si les primitives sont réalisés en temps constant,
la complexité du parcours est en O(N) (où N est le nombre de
sommets).
Il Existe 3 types de parcours :
1. parcours dans l’ordre préfixe
2. parcours dans l’ordre infixe ou symétrique
3. parcours dans l’ordre postfixe
Prenons l’exemple de l’arbre binaire AB sur lequel nous allons établir
l’ordre de parcours des sommets selon la stratégie adoptée.

7. 3.2 Arbre
binaire
Parcours préfixe
Consiste à effectuer récursivement le
parcours en suivant cet ordre :
1. consulter la valeur de la racine
2. parcourir le sous-arbre gauche
3. parcourir le sous-arbre droit
L’ordre de parcours pour les sommets
de l’arbre AB sera : a b d e h c f i j g k.
7

8. 3.2 Arbre
binaire
Parcours infixe ou symétrique
Consiste à effectuer récursivement le
parcours en suivant cet ordre :
1. parcourir le sous-arbre gauche
2. consulter la valeur de la racine
3. parcourir le sous-arbre droit
L’ordre de parcours pour les sommets de
l’arbre AB sera : d b h e a f j i c k g.
8

9. 3.2 Arbre
binaire
Parcours postfixe
Consiste à effectuer récursivement le
parcours en suivant cet ordre :
1. parcourir le sous-arbre gauche
2. parcourir le sous-arbre droit
3. consulter la valeur de la racine
L’ordre de parcours pour les sommets de
l’arbre AB sera : d h e b j i f k g c a.
9

10. 3.2 Arbre
binaire
10
Arbres binaires particuliers
Définition .3: On appelle arbre binaire complet un arbre binaire tel que
chaque sommet possède 0 ou 2 fils.
Théorème .4: Un arbre binaire complet possède 2P + 1 sommets (nombre
impair) dont P sommets internes et P + 1 feuilles.
Définition .5 On appelle arbre binaire parfait un arbre binaire
(complet) tel que chaque sommet soit père de deux sous arbres de
même hauteur.
Théorème .6 Un arbre binaire parfait possède 2h+1
− 1 sommets, où h
est la hauteur de l’arbre.
Définition .7 Un arbre binaire est plein s’il est complet et toutes ses
feuilles sont au même niveau.

11. Représentation d'un arbre quelconque sous forme
d'un arbre binaire
L'intérêt de l‘étude des arbres binaires tient du fait que tout arbre
ordonné A peut être représenté par un arbre binaire AB. Les
règles de passage sont les suivantes :
• Il y a une correspondance biunivoque entre les nœuds de A et
de AB.
• Le premier fils d'un nœud A est le successeur gauche du nœud
correspondant dans AB.
• Les autres fils d'un nœud A sont les successeurs droits de ce
nœud dans AB. Ils forment une chaine. Les liens directs des fils
avec le père sont supprimés.

13. Implémentations des arbres binaires sous forme
d’un tableau

17. ▪ Si on effectue des suppressions de sommets, il va falloir faire des
décalages pour éviter les trous dans le tableau. Pas simple car il ne
faut pas seulement décaler, il faut mettre a jour les bons numéros.
▪ On peut aussi accepter d'avoir des trous si on n'utilise pas les
primitives ci-dessus pour père et racine. Il faut cependant modifier
créer sommet pour trouver la première place libre dans le tableau
(qui n'est pas forcement nbSommets).
▪ Sinon on va consommer beaucoup de place mémoire qu'on n'utilisera
pas. En outre, pour indiquer qu'une "place est vide", il faut un
élément spécial élément-vide, ce qui n'est pas toujours possible
suivant la nature des éléments.

18. La primitive père pouvant être plus simplement la consultation du champ
tableau père. Si c'est une primitive, il faut impérativement utiliser la variable p
au lieu d'appeler plusieurs fois la primitive.

19. Implémentations des arbres binaires sous forme de
liste chainée
Un arbre est donc donne par l'adresse
de sa racine.

21. Plutôt long comme primitive, donc si
c'est souvent utilise, il est plus intelligent
de rajouter un pointeur vers le père dans
la structure

22. Quelques primitives de constructions/modifications :

24. 3.3 Arbre quelconque
24
Arbre général:
Dans un arbre général chaque sommet peut avoir un nombre
quelconque de fils. On ne distingue pas gauche, ou droit, ou centre. Il
y a tout de même un ordre sur les fils. Le 3ème ou le 7ème fils, ce
n’est pas la même chose.
Définition . Un arbre est dit ordonné si l’ordre relatif des sous-arbres
est important, est il est dit non-ordonné ou orienté dans le cas
contraire.

25. 3.3 Arbre quelconque
25
Primitives:
– racine(A : arbre) : sommet; retourne la racine
– premier_fils(x : sommet, A : arbre) : sommet; retourne le fils le plus à
gauche, ou VIDE
– frère(x : sommet, A : arbre) : sommet ; le premier frère à sa droite
– père(x : sommet, A : arbre) : sommet
– ieme _fils(x : sommet, i : entier, A : arbre) : sommet
– val(x : sommet, A : arbre) :élément
– arbre_est_vide(A : arbre) : booleen
– existe_fils(x : sommet, A : arbre) : booleen
– existe_frère(x : sommet, A : arbre) : booleen
– créer_vide() :arbre
– créer_sommet(e :élément, A : arbre)
– fait_racine(x : sommet, A : arbre)
– inserer_fils(pere : sommet,nouv : sommet, place : entier, A : arbre)
– supprimer_feuille(x : sommet, A : arbre)
– …

26. 3.3 Arbre quelconque
Parcours
But : passer en revue chaque sommet de l’arbre.
Parcours en profondeur
Parcours à main gauche. On veut les sommets dans cet
ordre
26

27. 3.3 Arbre quelconque
Parcours en profondeur peut faire du récursif, comme avec les arbres
binaires :
27

28. 3.3 Arbre quelconque
Méthode itérative l’algorithme de
Trémaux :
28

29. 3.3 Arbre quelconque
Parcours en largeur :Parcours hiérarchique, ou militaire. On veut les
sommets dans cet ordre
29

30. 3.3 Arbre quelconque
Implémentation contigüe:
30

31. 3.3 Arbre quelconque
Implémentation chainée:
31

35. Avec les tableau ce n'est plus du temps constant, c'est linéaire en N.
Et c'est pareil pour la primitive père, avec des tableaux ou avec des
pointeurs. Que faire pour avoir du temps constant ?
Solution 1 : rajouter l'info dans la structure de données :

36. L'adjonction de la racine ne pose pas de problèmes. Mais pour le père, ca
coute tout de même de la place mémoire. Et puis il faut faire attention a
rajouter dans les primitives la mise a jour de cette information.
Solution 2 : construire l'information uniquement quand on en a besoin.

37. 3.4 Arbre binaire de recherche
37
Arbre binaire de Recherche
Dans les méthodes classiques de recherche, en représentant l’ensemble
des éléments par un tableau (liste linéaire implémentée de manière
contigüe), on peut faire de la recherche en O(logN) par une méthode
dichotomique. C’est une bonne complexité, mais cette structure de
données est mauvaise si on veut faire des ajouts ou des suppressions, à
cause des décalages (complexité O(N)). Il faut trouver une structure de
données offrant une recherche aussi bien, càd en O(logN) aussi. Cela
existe, c’est l’arbre binaire de recherche.
Définition. Un arbre binaire de recherche est un arbre binaire tel que
la valeur stockée dans chaque sommet est supérieure à celles
stockées dans son sous-arbre gauche et inferieure à celles de son
sous-arbre droit.
Remarque : les éléments stockés dans l’arbre peuvent être compliqués.

39. 3.4 Arbre binaire de recherche
Arbre binaire de
Recherche
39

40. 3.4 Arbre binaire de recherche
40

41. 3.4 Arbre binaire de recherche
Ajout
Ajout d’un élément dans un arbre binaire de Recherche : On suppose que l’
élément n’est pas déjà dans l’arbre.
41

42. 3.4 Arbre binaire de recherche
42

43. 3.4 Arbre binaire de recherche
43
Ici, on ajoute le sommet en tant que feuille. On pourrait aussi ajouter en
tant que racine :
• couper l’arbre en deux sous-arbres (binaires de recherche) G et D, G
contenant tous les éléments de valeur plus petite que celle à ajouter,
et D contenant tous les éléments de valeur plus grande que celle à
ajouter,
• créer un nouveau sommet de valeur voulue en lui mettant G
comme sous-arbre gauche et D comme sous-arbre droit.
Exemple : Ajout de l’élément 32 dans l’arbre binaire de recherche AB :

44. 3.4 Arbre binaire de recherche
44

45. 3.4 Arbre binaire de recherche
45
Suppression
La suppression commence par la recherche de l’élément. Puis :
• si c’est une feuille, on la supprime sans problèmes
• si c’est un sommet qui n’a qu’un fils, on le remplace par ce fils
• si c’est un sommet qui a deux fils, on a deux solutions :
-le remplacer par le sommet de plus grande valeur dans le sous-arbre
gauche
- le remplacer par le sommet de plus petite valeur dans le sous-arbre
droit puis supprimer (récursivement) ce sommet.
Exemple : Suppression de l’élément 37 dans l’arbre binaire de recherche
AB :

46. 3.4 Arbre binaire de recherche
46

47. 3.4 Arbre binaire de recherche
47

48. 3.4 Arbre binaire de recherche
Arbres binaires de recherche équilibrés
La complexité de tous ces algorithmes est majorée par la hauteur de
l’arbre. On a donc intérêt à avoir des arbres les moins hauts possible.
Ainsi, pour améliorer ces algorithmes, on pourrait donc faire un
rééquilibrage de temps à autres, c’est à dire : récupérer tous les éléments
par un parcours symétrique, puis reconstruire un arbre quasi-parfait à
partir de ces éléments (tout en gardant son critère d’arbre binaire de
recherche).
48

49. 3.4 Arbre binaire de recherche
49
On peut chercher à avoir tout le temps un arbre de moindre hauteur, c’est
à dire un arbre tel que les hauteurs des sous-arbres de chaque sommet
diffèrent d’au plus 1 (i.e. un arbre parfait grignoté d’un étage à gauche, à
droite, au milieu, ...), et donc rééquilibrer comme il faut après chaque
ajout ou suppression.
On pourrait appeler un tel arbre : arbre AVL, du nom de leurs inventeurs
Adelson, Velskii et Landis.
Arbres A.V.L:
Définition .8: Un arbre binaire est dit H-équilibré si en tout sommet de
l’arbre les hauteurs des sous-arbres gauche et droit diffèrent au plus de 1.
Théorème .9: La hauteur d’un arbre H-équilibré est en O(logN).
Définition .10: Un arbre AVL est un arbre binaire de recherche H-
équilibré.
Donc dans un AVL :
– la recherche d’un élément est en O(logN) puisque la hauteur est en O(logN)

50. 3.4 Arbre binaire de recherche
Exemple :
Le problème de maintenance de la propriété AVL se pose au moment de
l’insertion ou de l’effacement d’un élément.
Supposons qu’un nouvel élément soit inséré dans les feuilles de l’arbre. Cette
insertion peut entrainer un déséquilibre de l’arbre, qui cessera alors d’être
un arbre AVL.
Exemple : Ici l’arbre n’est plus AVL, puisque le sous-arbre gauche du nœud
20 a pour longueur 2, alors que le sous-arbre de droite a pour longueur 0.
50

51. 3.4 Arbre binaire de recherche
Dans d’autres cas, la propriété AVL peut être conservée.
Ainsi :
On dira donc qu’un nœud est équilibré si les chemins les plus longs, dans
chaque sous arbre partant d’un nœud, sont égaux. Si le chemin du sous
arbre est plus long d’une unité que celui de droite, on dira qu’il est lourd
à gauche. Inversement, si le nœud n’est ni équilibré ni lourd à gauche, il
sera lourd à droite. Dans un arbre AVL, chaque nœud se trouve dans l’un
de ces états.
51

52. 3.4 Arbre binaire de recherche
52
Ajout d’un élément dans un arbre AVL
Cela provoque un changement d’état d’un ou de plusieurs nœuds. Les trois
cas possibles sont les suivants :
1. Un nœud équilibré devient lourd à droite ou lourd à gauche.
2. Un nœud lourd (à gauche ou à droite) devient équilibré.
3. Un nœud lourd (à gauche ou à droite) devient totalement déséquilibré
par l’insertion
d’un nouvel élément dans le sous-arbre déjà lourd. On dit que le nœud
correspondant devient critique.
• Les deux premiers cas ne changent pas la propriété AVL de l’arbre.
• Dans le 3ème
cas il convient de réorganiser l’arbre pour lui permettre de
conserver sa
propriété AVL.
Les trois possibilités peuvent être représentées de la manière suivante :

53. 3.4 Arbre binaire de recherche
2 .Le second cas est plus complexe, et peut être
représenté par :
53

54. 3.4 Arbre binaire de recherche
Un élément est ajouté à gauche de B, ce qui déséquilibre le sous-arbre
gauche de A. pour parvenir à une structure équilibrée, il suffit d’effectuer
une rotation vers la droite qui place B à la racine. Le même cas peut se
présenter à droite.
3. Le 3ème
cas est représenté par :
54

55. 3.4 Arbre binaire de recherche
Si un élément est ajouté à l’un des sous-arbres de C le nœud A devient lourd à
gauche. Dans ce cas, pour rééquilibrer A il suffit d’effectuer une rotation
double, d’abord (B, C) à gauche, puis (C, A) à droite.
Exemple 1 : Le nœud critique est 20. On réequilible en appliquant la régle 1 :
55

56. 3.4 Arbre binaire de recherche
Exemple 2 : Le nœud critique est
14.
56

57. 3.4 Arbre binaire de recherche
L’arbre devient après
équilibrage :
57

58. 3.4 Arbre binaire de recherche
Exemple 3 : Le point critique est le
10.
58

59. 3.4 Arbre binaire de recherche
Devient après
équilibrage :
59

60. 3.5 Structure de données TAS
Définition: Un tas est un arbre binaire quasi-parfait tel que la valeur de
chaque sommet est inferieure à la valeur de (son ou) ses fil(s). Cette
structure de données permet en particulier de faire un tri super géant en
termes de complexité.
Implémentation d'un arbre binaire (quasi-)parfait:
On sait qu'il y aura un seul
élément au premier niveau,
2 au deuxième, 4 au
troisième, ..., 2i
au ième
, ...

61. Tri pas tas
‒ Le tri par tas comporte les étapes suivantes :
• Construire un tas contenant les éléments a trier
• soit en ajoutant les éléments un par un
• soit en construisant directement le tas
‒ éplucher le tas c'est a dire :
• écrire la racine (qui est le plus petit élément)
• la supprimer et réorganiser pour que ca reste un tas
• recommencer jusqu'a ce que le tas soit vide.
3.5 Structure de données TAS

62. Ajout d'un élément dans le tas
3.5 Structure de données TAS
On ajoute le sommet en tant que première feuille possible (a la fin du
tableau) puis on l‘échange avec son père jusqu'a ce que ca forme de
nouveau un tas.

63. 3.5 Structure de données TAS

64. 3.5 Structure de données TAS
Epluchage
"Eplucher" c'est retourner le plus petit élément du tas, le supprimer et
faire en sorte que ce qui reste soit toujours un tas, cela est réalise comme
suit :
• on retourne la racine (le plus petit élément).
• on met la dernière feuille a la place de la racine (on la supprime).
• on fait descendre cette "racine" a sa bonne place en l‘échangeant avec
le plus petit de ses deux fils.

65. 3.5 Structure de données TAS

66. 3.5 Structure de données TAS

67. 3.5 Structure de données TAS
La complexité est majorée par la hauteur de l'arbre binaire. Comme
l'arbre est quasi parfait, on obtient O(logN) .

68. Exemple de tri par TAS
3.5 Structure de données TAS
Etant donnes la suite d‘éléments entiers a trier, arrivant dans cet ordre :
30, 21, 4, 10, 36, 17, 20, 8, 11, 5. Le tri se fait en construisant tout d'abord
le TAS en insérant les éléments un a un, et ensuite en faisant son
épluchage.
1) Construction du TAS
Insérer l‘élément de valeur 30 :
Insérer l‘élément de valeur 21 :

69. 3.5 Structure de données TAS
Insérer l‘élément de valeur 4 :
Insérer l‘élément de valeur 36 :
Insérer l‘élément de valeur 10 :

70. 3.5 Structure de données TAS
Insérer l‘élément de valeur 17 :
Insérer l‘élément de valeur 20 :
Insérer l‘élément de valeur 8 :

71. 3.5 Structure de données TAS
Insérer l‘élément de valeur 11 :
Insérer l‘élément de valeur 5 :

72. 2) épluchage du TAS
3.5 Structure de données TAS
Le résultat du tri par ordre croissant correspond a la séquence des valeurs lus
lors de l‘étape d‘épluchage du TAS.
Lire la racine 4 puis la supprimer du TAS :

73. Lire la racine 5 puis la supprimer du TAS :
Lire la racine 8 puis la supprimer du TAS :

74. Lire la racine 10 puis la supprimer du TAS :
Lire la racine 11 puis la supprimer du TAS :

75. Lire la racine 17 puis la supprimer du TAS :
Lire la racine 20 puis la supprimer du TAS :

76. Lire la racine 21 puis la supprimer du TAS :
Lire la racine 30 puis la supprimer du TAS :
Lire la racine 36 puis la supprimer du TAS ce qui donnera un TAS vide à la fin.

77. Exercices & Solutions sur les Arbres
77
Exercice 1:
Calculer la hauteur d'un arbre en vous basant sur la définition
récursive :
- un arbre vide est de hauteur 0 ;
-un arbre non vide a pour hauteur 1 + la hauteur maximale
entre ses fils.

78. Exercices & Solutions sur les Arbres
78
Solution 1:
fonction hauteur(R: sommet , T : arbre ):entier
Debut
si (Vide( R )) renvoyer 0
sinon renvoyer 1 + max (hauteur ( FilsGauche(R, T) , T) ,
hauteur(FilsDroit(R,T), T) )
finsi
Fin

79. Exercices & Solutions sur les Arbres
3
86
9
15
27
48
Root
42
12
79

80. Exercices & Solutions sur les Arbres
80
Exercice 2:
Calculer le nombre de nœuds en vous basant sur la définition
récursive :
- si l'arbre est vide : renvoyer 0 ;
-sinon renvoyer 1 plus la somme du nombre de nœuds des sous-
arbres.

81. Exercices & Solutions sur les Arbres
81
Solution 2
fonction NombreNœud(R: sommet, T : arbre ): entier
debut
si (Vide( R )) renvoyer 0;
sinon renvoyer 1 + NombreNœud(FilsGauche(R, T), T) +
NombreNœud(FilsDroit(R, T), T);
finsi
fin

82. Exercices & Solutions sur les Arbres
82
Exercice 3:
Calculer le nombre de feuilles en vous basant sur la définition
récursive :
un arbre vide n'a pas de feuille ;
un arbre non vide a son nombre de feuilles défini de la façon
suivante :
• si le nœud est une feuille, alors on renvoie 1,
• si c'est un nœud interne, alors le nombre de feuilles est la
somme du nombre de feuilles de chacun de ses fils.

83. Exercices & Solutions sur les Arbres
83
Solution 3:
fonction NombreFeuilles (R: sommet ,T : arbre ):entier
Debut
si (Vide( R)) alors renvoyer 0;
sinon si (feuille (R, T)) alors renvoyer 1
sinon renvoyer NombreFeuilles( FilsGauche(R,T), T) +
NombreFeuilles( FilsDroit(R, T), T );
Finsi
fin

84. Exercices & Solutions sur les Arbres
84
Exercice 4:
Calculer le nombre de nœuds internes en vous basant sur la
définition récursive :
un arbre vide n'a pas de nœud interne.
si le nœud en cours n'a pas de fils alors renvoyer 0
si le nœud a au moins un fils, renvoyer 1 plus la somme des
nœuds interne des sous-arbres.

85. Exercices & Solutions sur les Arbres
85
Solution 4:
fonction NombreNoeudsInternes(R: sommet , T : arbre ):entier
Debut
si (Vide( R)) alors renvoyer 0;
sinon si (Feuille(R)) alors renvoyer 0 ;
sinon renvoyer 1 + NombreNoeudsInternes(FilsGauche(R,T), T) +
NombreNoeudsInternes(FilsDroit(R,T), T);
finsi
fin