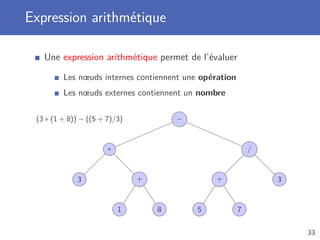
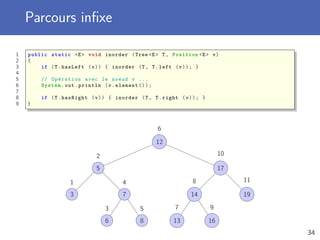
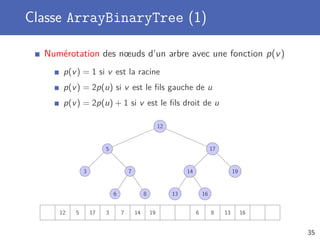
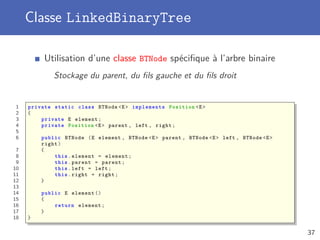
Le document traite de la programmation orientée objet avec un accent particulier sur les arbres et les algorithmes de recherche. Il présente les concepts de structures de données, les différentes propriétés des arbres, leurs implémentations, ainsi que les algorithmes de parcours et de recherche. Des exemples de méthodes spécifiques pour manipuler des arbres binaires et leur utilisation dans divers contextes sont également fournis.

1. PO3T Programmation orientée objet
Séance 7
Arbre et algorithme
de recherche
Sébastien Combéfis, Quentin Lurkin lundi 9 novembre 2015

2. Ce(tte) œuvre est mise à disposition selon les termes de la Licence Creative Commons
Attribution – Pas d’Utilisation Commerciale – Pas de Modification 4.0 International.

3. Rappels
Structure de données et complexités
Type abstrait de données (TAD)
Complexité temporelle des méthodes
Complexité spatiale de la structure de données
TAD pour représenter des séquences d’éléments
Pile, file, deque et vecteur
Implémentation par structure chainée
Classe interne pour cacher l’implémentation
3

4. Objectifs
Arbre
Le TAD Tree
Implémentation par tableau ou structure chainée
Le TAD BinaryTree
Algorithme de recherche
Recherche séquentielle et dichotomique
Le TAD BinarySearchTree
4

5. Arbre

6. TAD Arbre (1)
Un arbre stocke des éléments de manière hiérarchique (tree)
Tout élément possède un parent et zéro, un ou plusieurs enfants
La racine de l’arbre n’a pas de parent
Un arbre possède une unique racine
Bière
Trappiste
Rochefort 8
Trappe
Quadruple
Abbaye
Leffe Rituel
Autre
Maes Raedler CaraPils
6

7. Propriétés des arbres (1)
Ensemble de nœuds liés par une relation parent-enfant
Un arbre non vide possède une racine (qui n’a pas de parent)
Les nœuds v ont un parent unique w (v est enfant de w)
Chaque nœud de l’arbre stocke un élément
Deux nœuds avec le même parent sont frère/sœur (siblings)
Un nœud externe (feuille) n’a pas d’enfants (leaf)
Un nœud interne a un ou plusieurs enfants
7

8. Propriétés des arbres (2)
Le nœud u est un ancêtre du nœud v
si u = v
ou si u est un ancêtre du parent de v
Nœud v descendant de u si u ancêtre de v
Sous-arbre enraciné en un nœud v
Arbre avec v en racine et tous ses descendants comme nœuds
8

9. Propriétés des arbres (3)
Bière
Trappiste
Rochefort 8
Trappe
Quadruple
Abbaye
Leffe Rituel
Autre
Maes Raedler CaraPils
Racine
frère/sœur
parent/enfant
ancêtre/descendant
Nœud interne
Nœud externe
Trappiste parent de Rochefort 8 et Rochefort 8 enfant de Trappiste
Bière ancêtre de CaraPils et CaraPils descendant de Bière
9

10. TAD Arbre (2)
Méthodes spécifiques au TAD arbre
root() renvoie la racine de l’arbre (erreur si vide)
parent(v) renvoie le parent de v (erreur si racine)
children(v) renvoie un itérateur des enfants de v
Méthodes d’interrogation de l’arbre
isInternal(v) teste si v est un nœud interne
isExternal(v) teste si v est un nœud externe
isRoot(v) teste si v est la racine
10

11. TAD Arbre (3)
Méthodes de mise à jour
Décrites plus loin...
Méthodes additionnelles
size() renvoie la taille de l’arbre
isEmpty() teste si l’arbre est vide
elements() renvoie un itérateur des éléments de l’arbre
positions() renvoie un itérateur des nœuds de l’arbre
replace(v, e) remplace l’élément du nœud v par e et renvoie
l’élément qui s’y trouvait avant
11

12. Interface Tree (1)
1 public interface Tree <E>
2 {
3 public Position <E> root () throws EmptyTreeException ;
4
5 public Position <E> parent (Position <E> v)
6 throws InvalidPositionException , BoundaryViolationException ;
7
8 public Iterator <Position <E>> children (Position <E> v)
9 throws InvalidPositionException ;
10
11 public boolean isInternal (Position <E> v) throws InvalidPositionException ;
12
13 public boolean isExternal (Position <E> v) throws InvalidPositionException ;
14
15 public boolean isRoot (Position <E> v) throws InvalidPositionException ;
16
17 public int size ();
18
19 public boolean isEmpty ();
20
21 public Iterator <E> elements ();
22
23 public Iterator <Position <E>> positions ();
24
25 public E replace (Position <E> v, E e) throws InvalidPositionException ;
26 }
12

13. Interface Tree (2)
EmptyTreeException lorsque opération sur arbre vide
Ne devrait jamais arriver puisqu’on connait la taille de l’arbre
InvalidPositionException pour position pas dans l’arbre
Ne devrait jamais arriver car on reçoit les positions de l’arbre
BoundaryViolationException si opération sur la racine
Ne devrait jamais arriver puisqu’on sait tester la racine
13

14. Profondeur
La profondeur de v est son nombre d’ancêtres (v exclu)
Mesure de la distance par rapport à la racine
La racine est à une profondeur de zéro
1 public static <E> int depth (Tree <E> T, Position <E> v)
2 {
3 if (T.isRoot (v))
4 {
5 return 0;
6 }
7 return 1 + depth (T, T.parent (v));
8 }
14

15. Hauteur
La hauteur se définit aussi récursivement
Un nœud externe a une hauteur de zéro
La hauteur de v vaut 1 plus la hauteur maximale de ses enfants
La hauteur d’un arbre non vide est celle de sa racine
1 public static <E> int height (Tree <E> T, Position <E> v)
2 {
3 if (T.isExternal (v))
4 {
5 return 0;
6 }
7
8 int h = 0;
9 for (Position <E> child : T.children (v))
10 {
11 h = Math.max (h, height (T, child))
12 }
13 return 1 + h;
14 }
15

16. Parcours d’un arbre
Un parcours d’arbre traverse tous ses nœuds
Traversée systématique, visite de tous les nœuds
Deux principaux types de parcours
Préfixe : racine puis chaque sous-arbre
Postfixe : chaque sous-arbre puis racine
A
B C D
G H
E
I
F
16

17. Parcours préfixe
A B C D G H E I F
1 public static <E> void preorder (Tree <E> T, Position <E> v)
2 {
3 // Opération avec le noeud v ...
4 System.out.println (v.element ());
5
6 for (Position <E> child : T.children (v))
7 {
8 preorder (T, child);
9 }
10 }
A
1
B
2
C
3
D
4
G
5
H
6
E 7
I 8
F
9
17

18. Structure d’un document
Parcours préfixe utilisé pour parcourir un document
Si on représente la structure en chapitres/sections/...
Rapport
Intro Chap 1 Chap 2
Sec 1.1 Sec 1.2
Chap 3
Sec 3.1
Conclu
18

19. Parcours postfixe
B C G H D I E F A
1 public static <E> void postorder (Tree <E> T, Position <E> v)
2 {
3 for (Position <E> child : T.children (v))
4 {
5 postorder (T, child);
6 }
7
8 // Opération avec le noeud v ...
9 System.out.println (v.element ());
10 }
A
9
B
1
C
2
D
5
G
3
H
4
E 7
I 6
F
8
19

20. Système de fichiers
Parcours postfixe utilisé pour calculer la taille d’un répertoire
Il faut sommer la taille du contenu du répertoire
/home/combefis/ecam/2015/coo
planning.pdf
12 Ko
students.xlsx
42 Ko
slides
cours1.pdf
1.17 Mo
cours2.pdf
2.24 Mo
examens
jan2015.pdf
122 Ko
secret.txt
18 Ko
20

21. Interface Position
Nœuds de l’arbre représentés par l’interface Position
element() renvoie l’élément stocké dans le nœud
La position stocke l’élément et d’autres informations
Informations sur la structure de l’arbre et les liens entre nœuds
1 public interface Position <E>
2 {
3 public E element ();
4 }
21

22. Classe LinkedTree (1)
1 public class LinkedTree <E> implements Tree <E>
2 {
3 private Position <E> root;
4 private int size;
5
6 public LinkedTree ()
7 {
8 root = null;
9 size = 0;
10 }
11
12 private static class TreeNode <E> implements Position <E>
13 {
14 private E element;
15 private TreeNode <E> parent;
16 private List <TreeNode <E>> children;
17
18 public TreeNode (E element , TreeNode <E> parent)
19 {
20 this.element = element;
21 this.parent = parent;
22 this.children = new LinkedList <TreeNode <E>>();
23 }
24
25 public E element ()
26 {
27 return element;
28 }
29 }
22

23. Classe LinkedTree (2)
1 public Position <E> root () throws EmptyTreeException
2 {
3 if (root == null)
4 {
5 throw new EmptyTreeException ();
6 }
7 return root;
8 }
9
10 public int size ()
11 {
12 return size;
13 }
14
15 public boolean isEmpty ()
16 {
17 return size == 0;
18 }
23

24. Classe LinkedTree (3)
1 private TreeNode <E> checkPosition (Position <E> v) throws
InvalidPositionException
2 {
3 if (! (v instanceof TreeNode))
4 {
5 throw new InvalidPositionException ();
6 }
7 return (TreeNode <E>) v;
8 }
9
10 public Position <E> parent (Position <E> v) throws InvalidPositionException ,
BoundaryViolationException
11 {
12 if (isRoot (v))
13 {
14 throw new BoundaryViolationException ();
15 }
16 return (( TreeNode <E>) v).parent;
17 }
18
19 public Iterator <Position <E>> children (Position <E> v) throws
InvalidPositionException
20 {
21 TreeNode <E> tn = checkPosition (v);
22 List <Position <E>> children = new LinkedList <Position <E>>();
23 for (TreeNode <E> p : tn.children)
24 {
25 children.add (p);
26 }
27 return children.iterator (); 24

25. Classe LinkedTree (4)
1 public boolean isInternal (Position <E> v) throws InvalidPositionException
2 {
3 return ! isExternal (v);
4 }
5
6 public boolean isExternal (Position <E> v) throws InvalidPositionException
7 {
8 TreeNode <E> tn = checkPosition (v);
9 return tn.children.isEmpty ();
10 }
11
12 public boolean isRoot (Position <E> v) throws InvalidPositionException
13 {
14 checkPosition (v);
15 return v == root;
16 }
17
18 public E replace (Position <E> v, E e) throws InvalidPositionException
19 {
20 TreeNode <E> tn = checkPosition (v);
21 E old = tn.element;
22 tn.element = e;
23 return old;
24 }
25
26 // ... et elements () et positions () non implémentés .
27 }
25

26. Arbre binaire

27. Arbre ordonné et binaire
Un arbre ordonné définit un ordre pour les enfants des nœuds
On peut définir le premier enfant, le deuxième...
Un arbre binaire est un arbre ordonné tel que
Chaque nœud possède au maximum deux enfants
Chaque nœud est soit un fils gauche, soit un fils droit
Le fils gauche précède le fils droit dans l’ordre des enfants
Sous-arbres gauche et droit pour chaque nœud
27

28. Propriétés des arbres binaires
Un arbre binaire peut être propre (ou impropre)
Chaque nœud possède zéro ou deux enfants
Une arête d’un arbre est une paire (u, v) avec u parent de v
Un arbre possède au maximum 2h+1 − 1 nœuds
A
B
D E
C
28

29. TAD Arbre Binaire (1)
Les nœuds d’arbre binaire ont max deux enfants (binary tree)
Un nœud est le fils gauche ou le fils droit
Méthodes spécifiques au TAD arbre binaire
left(v) renvoie le fils gauche de v (erreur si absent)
right(v) renvoie le fils droit de v (erreur si absent)
hasLeft(v) teste si v a un fils gauche
hasRight(v) teste si v a un fils droit
29

30. TAD Arbre Binaire (2)
Méthodes de mise à jour
addRoot(e) crée et renvoie un nœud stockant e et en fait la
racine de l’arbre (erreur si arbre non vide)
insertLeft(v, e) crée et renvoie un nœud stockant e et en fait
le fils gauche de v (erreur si déjà fils gauche)
insertRight(v, e) crée et renvoie un nœud stockant e et en
fait le fils droit de v (erreur si déjà fils droit)
remove(v) supprime le nœud v et le remplace par son fils (erreur
si deux fils)
attach(v, T1, T2) attache T1 et T2 comme sous-arbres gauche
et droit du nœud v (erreur si v interne)
30

31. Interface BinaryTree
L’interface BinaryTree étend l’interface Tree
La méthode children renvoie les fils dans le bon ordre
1 public interface BinaryTree <E> extends Tree <E>
2 {
3 public Position <E> left (Position <E> v)
4 throws InvalidPositionException , BoundaryViolationException ;
5
6 public Position <E> right (Position <E> v)
7 throws InvalidPositionException , BoundaryViolationException ;
8
9 public boolean hasLeft (Position <E> v) throws InvalidPositionException ;
10
11 public boolean hasRight (Position <E> v) throws InvalidPositionException ;
12 }
31

32. Arbre de décision
Un arbre de décision représente un processus de décision
Les nœuds internes contiennent une question
Les nœuds externes contiennent une décision
Les arêtes sont étiquetées avec Oui/Non
Y a-t-il du soleil ?
On est en décembre ?
On fait une raclette !
Oui
On fait un BBQ !
Non
Oui
On dort !
Non
32

33. Expression arithmétique
Une expression arithmétique permet de l’évaluer
Les nœuds internes contiennent une opération
Les nœuds externes contiennent un nombre
(3 ∗ (1 + 8)) − ((5 + 7)/3) −
∗
3 +
1 8
/
+
5 7
3
33

34. Parcours infixe
1 public static <E> void inorder (Tree <E> T, Position <E> v)
2 {
3 if (T.hasLeft (v)) { inorder (T, T.left (v)); }
4
5 // Opération avec le noeud v ...
6 System.out.println (v.element ());
7
8 if (T.hasRight (v)) { inorder (T, T.right (v)); }
9 }
12
6
5
2
3
1
7
4
6
3
8
5
17
10
14
8
13
7
16
9
19
11
34

35. Classe ArrayBinaryTree (1)
Numérotation des nœuds d’un arbre avec une fonction p(v)
p(v) = 1 si v est la racine
p(v) = 2p(u) si v est le fils gauche de u
p(v) = 2p(u) + 1 si v est le fils droit de u
12
5
3 7
6 8
17
14
13 16
19
12 5 17 3 7 14 19 6 8 13 16
35

36. Complexité de ArrayBinaryTree
Complexité temporelle des opérations
Méthode Complexité
size, isEmpty O(1)
elements, positions O(n)
replace O(1)
root, parent, children, left, right O(1)
hasLeft, hasRight, isInternal, isExternal, isRoot O(1)
Complexité spatiale en O(2h+1 − 1)
En notant bien qu’il y a une capacité maximale fixée
36

37. Classe LinkedBinaryTree
Utilisation d’une classe BTNode spécifique à l’arbre binaire
Stockage du parent, du fils gauche et du fils droit
1 private static class BTNode <E> implements Position <E>
2 {
3 private E element;
4 private Position <E> parent , left , right;
5
6 public BTNode (E element , BTNode <E> parent , BTNode <E> left , BTNode <E>
right)
7 {
8 this.element = element;
9 this.parent = parent;
10 this.left = left;
11 this.right = right;
12 }
13
14 public E element ()
15 {
16 return element;
17 }
18 }
37

38. Complexité de LinkedBinaryTree
Complexité temporelle des opérations
Méthode Complexité
size, isEmpty O(1)
elements, positions O(n)
replace O(1)
root, parent, children, left, right O(1)
hasLeft, hasRight, isInternal, isExternal, isRoot O(1)
insertLeft, insertRight, attach, remove O(1)
Complexité spatiale en O(n)
Il y a exactement un nœud par élément de l’arbre
38

39. Définition récursive
Définition récursive d’un arbre binaire
Arbre vide
Un nœud avec un élément et sous-arbres binaires gauche et droit
1 public class RecursiveBT <E>
2 {
3 private final E element;
4 private final RecursiveBT <E> left , right;
5
6 public RecursiveBT (E element , RecursiveBT <E> left , RecursiveBT <E> right)
7 {
8 this.element = element;
9 this.left = left;
10 this.right = right;
11 }
12 }
39

40. Algorithme de recherche

41. Recherche linéaire
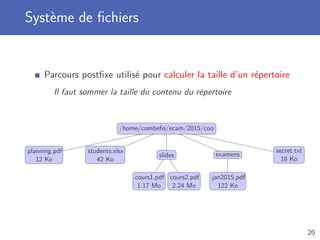
Parcours de la structure de donnée, élément par élément
Jusqu’à trouver l’élément ou avoir parcouru toute la structure
Complexité temporelle en O(n)
Dans le pire des cas, tous les élément sont parcourus
1 public static boolean find (int [] data , int elem)
2 {
3 for (int i = 0; i < data.length; i++)
4 {
5 if (data[i] == elem)
6 {
7 return true;
8 }
9 }
10 return false;
11 }
41

42. Recherche dichotomique
Recherche plus efficace si les données sont triées
Il faut évidemment avant tout trier les données
Complexité temporelle en O(log n)
On réduit l’espace de recherche de moitié à chaque itération
Recherche de 44
4 6 9 11 12 17 21 23 40 41 44 49 51 59 92 99
start endmid
42

43. Recherche dichotomique
Recherche plus efficace si les données sont triées
Il faut évidemment avant tout trier les données
Complexité temporelle en O(log n)
On réduit l’espace de recherche de moitié à chaque itération
Recherche de 44
4 6 9 11 12 17 21 23 40 41 44 49 51 59 92 99
start endmid
42

44. Recherche dichotomique
Recherche plus efficace si les données sont triées
Il faut évidemment avant tout trier les données
Complexité temporelle en O(log n)
On réduit l’espace de recherche de moitié à chaque itération
Recherche de 44
4 6 9 11 12 17 21 23 40 41 44 49 51 59 92 99
start endmid
42

45. Recherche dichotomique
Recherche plus efficace si les données sont triées
Il faut évidemment avant tout trier les données
Complexité temporelle en O(log n)
On réduit l’espace de recherche de moitié à chaque itération
Recherche de 44
4 6 9 11 12 17 21 23 40 41 44 49 51 59 92 99
start endmid
42

46. Arbre Binaire de Recherche
Un arbre binaire de recherche est un arbre binaire propre
chaque nœud interne stocke un élément e
les éléments du sous-arbre gauche sont <= e
les éléments du sous-arbre droit sont >= e
tous les nœuds externes ne stockent aucun élément
Un parcours infixe permet un parcours par ordre croissant
Complexité temporelle de la recherche en O(h)
43

47. Recherche d’un élément
1 public static <E> boolean find (BinaryTree <E> T, E value)
2 {
3 return T.isInternal (search (T, T.root (), value));
4 }
5
6 private static <E> Position <E> search (BinaryTree <E> T, Position <E> v, E e)
7 {
8 if (T.isExternal (v))
9 {
10 return v;
11 }
12
13 if (e.compareTo (v.element ()) < 0)
14 {
15 return search (T, T.left (v), e);
16 }
17 else if (e.compareTo (v.element ()) > 0)
18 {
19 return search (T, T.right (v), e);
20 }
21 else
22 {
23 return v;
24 }
25 }
44

48. Autres arbres de recherche
Arbre AVL (AVL Tree)
Premier arbre binaire de recherche automatiquement équilibré
Arbre splay (Splay Tree)
Les éléments récemment accédés sont rapidement accessibles
Arbre (2, 4) ((2, 4) Tree)
Arbre général automatiquement équilibré
Arbre rouge et noir (Red-Black Tree)
Arbre binaire automatiquement équilibré
45

49. Crédits
https://www.flickr.com/photos/127497725@N02/16695848708
https://www.flickr.com/photos/arenamontanus/14770259458
https://www.flickr.com/photos/tudor/295942966
46