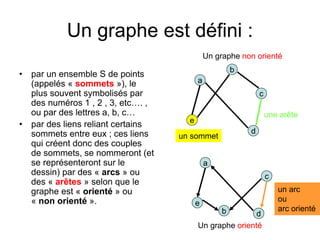
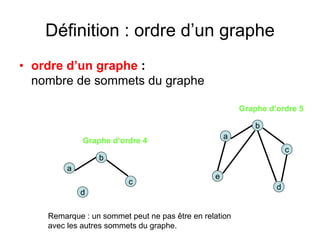
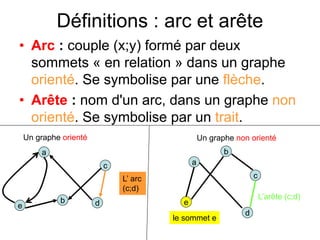
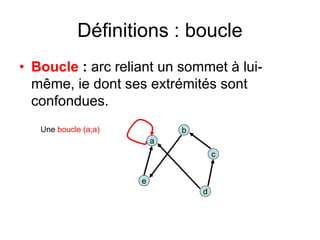
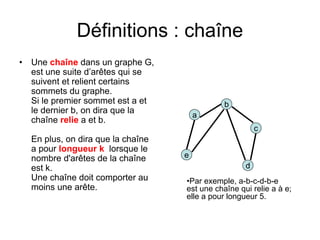
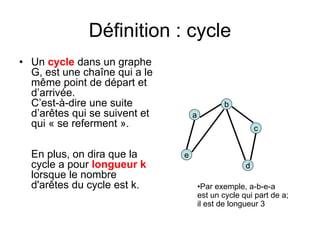
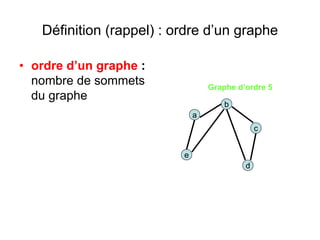
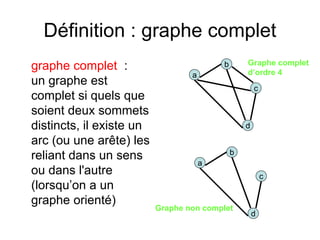
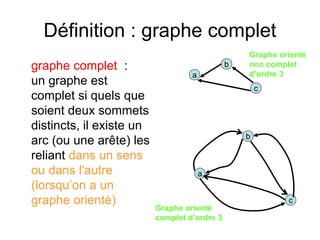
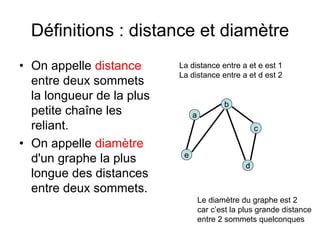
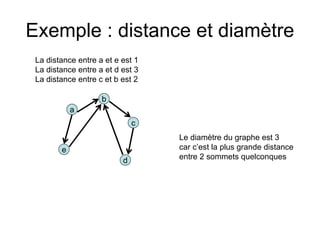
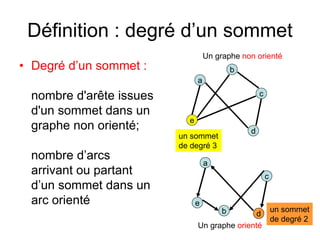
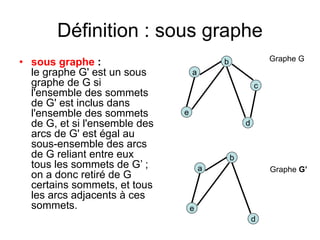
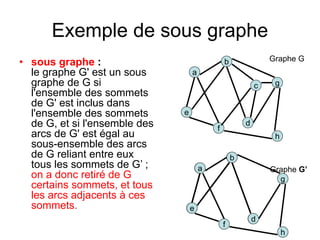
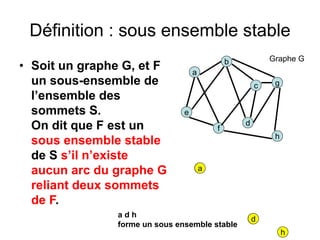
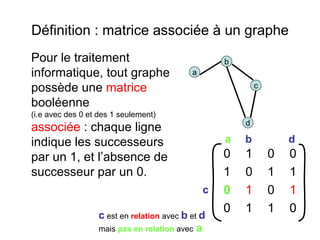
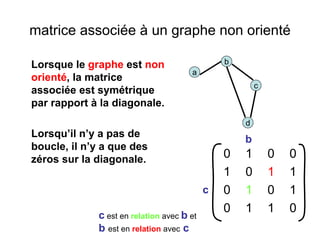
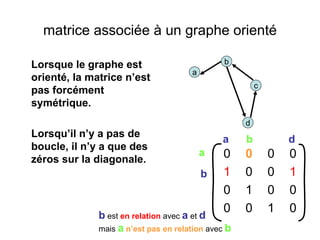
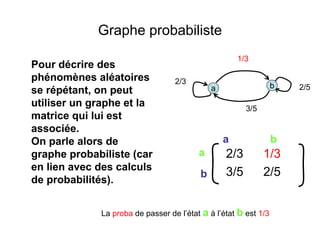
Le document présente une introduction à la théorie des graphes, en définissant des concepts clés tels que sommets, arcs, arêtes, chaînes et cycles. Il explique également des notions comme le degré d'un sommet, la distance entre deux sommets et les graphes complets. Enfin, il aborde les graphes orientés et non orientés, ainsi que la matrice associée à un graphe pour des applications informatiques.

1. Théorie des graphes
Un peu de vocabulaire
Présenté Par
Mohamed Bouhamed

2. Théorie des graphes
L’objectif est de décrire des objets
(d’où un vocabulaire spécifique) dont
nous aurons besoin pour résoudre
différents problèmes.

3. Un graphe est défini :
• par un ensemble S de points
(appelés « sommets »), le
plus souvent symbolisés par
des numéros 1 , 2 , 3, etc…. ,
ou par des lettres a, b, c…
• par des liens reliant certains
sommets entre eux ; ces liens
qui créent donc des couples
de sommets, se nommeront (et
se représenteront sur le
dessin) par des « arcs » ou
des « arêtes » selon que le
graphe est « orienté » ou
« non orienté ».
a
d
b
e
c
Un graphe non orienté
Un graphe orienté
a
db
e
c
une arête
un sommet
un arc
ou
arc orienté

4. Définition : ordre d’un graphe
• ordre d’un graphe :
nombre de sommets du graphe
a
d
b
e
c
Graphe d’ordre 5
a
d
b
c
Graphe d’ordre 4
Remarque : un sommet peut ne pas être en relation
avec les autres sommets du graphe.

5. Définitions : arc et arête
• Arc : couple (x;y) formé par deux
sommets « en relation » dans un graphe
orienté. Se symbolise par une flèche.
• Arête : nom d'un arc, dans un graphe non
orienté. Se symbolise par un trait.
a
d
b
e
c
Un graphe non orienté
L’arête (c;d)
le sommet e
Un graphe orienté
a
db
e
c
L’ arc
(c;d)

6. Définitions : boucle
• Boucle : arc reliant un sommet à lui-
même, ie dont ses extrémités sont
confondues.
a
d
b
e
c
Une boucle (a;a)

7. Définitions : chaîne
• Une chaîne dans un graphe G,
est une suite d’arêtes qui se
suivent et relient certains
sommets du graphe.
Si le premier sommet est a et
le dernier b, on dira que la
chaîne relie a et b.
En plus, on dira que la chaîne
a pour longueur k lorsque le
nombre d'arêtes de la chaîne
est k.
Une chaîne doit comporter au
moins une arête.
a
d
b
e
c
•Par exemple, a-b-c-d-b-e
est une chaîne qui relie a à e;
elle a pour longueur 5.

8. Définition : cycle
• Un cycle dans un graphe
G, est une chaîne qui a le
même point de départ et
d’arrivée.
C’est-à-dire une suite
d’arêtes qui se suivent et
qui « se referment ».
En plus, on dira que la
cycle a pour longueur k
lorsque le nombre
d'arêtes du cycle est k.
a
d
b
e
c
•Par exemple, a-b-e-a
est un cycle qui part de a;
il est de longueur 3

9. Définition (rappel) : ordre d’un graphe
• ordre d’un graphe :
nombre de sommets
du graphe
a
d
b
e
c
Graphe d’ordre 5

10. Définition : graphe complet
graphe complet :
un graphe est
complet si quels que
soient deux sommets
distincts, il existe un
arc (ou une arête) les
reliant dans un sens
ou dans l'autre
(lorsqu’on a un
graphe orienté)
a
d
b
c
a
d
b
c
Graphe non complet
Graphe complet
d’ordre 4

11. Définition : graphe complet
graphe complet :
un graphe est
complet si quels que
soient deux sommets
distincts, il existe un
arc (ou une arête) les
reliant dans un sens
ou dans l'autre
(lorsqu’on a un
graphe orienté)
a
b
c
Graphe orienté
complet d’ordre 3
Graphe orienté
non complet
d’ordre 3
a
b
c

12. Définitions : distance et diamètre
• On appelle distance
entre deux sommets
la longueur de la plus
petite chaîne les
reliant.
• On appelle diamètre
d'un graphe la plus
longue des distances
entre deux sommets.
a
d
b
e
c
La distance entre a et e est 1
La distance entre a et d est 2
Le diamètre du graphe est 2
car c’est la plus grande distance
entre 2 sommets quelconques

13. Exemple : distance et diamètre
a
d
b
e
c
La distance entre a et e est 1
La distance entre a et d est 3
La distance entre c et b est 2
Le diamètre du graphe est 3
car c’est la plus grande distance
entre 2 sommets quelconques

14. Définition : degré d’un sommet
• Degré d’un sommet :
nombre d'arête issues
d'un sommet dans un
graphe non orienté;
nombre d’arcs
arrivant ou partant
d’un sommet dans un
arc orienté
a
d
b
e
c
Un graphe non orienté
Un graphe orienté
a
db
e
c
un sommet
de degré 3
un sommet
de degré 2

15. Définition : sous graphe
• sous graphe :
le graphe G' est un sous
graphe de G si
l'ensemble des sommets
de G' est inclus dans
l'ensemble des sommets
de G, et si l'ensemble des
arcs de G' est égal au
sous-ensemble des arcs
de G reliant entre eux
tous les sommets de G’ ;
on a donc retiré de G
certains sommets, et tous
les arcs adjacents à ces
sommets.
a
d
b
e
c
Graphe G
Graphe G’a
d
b
e

16. Exemple de sous graphe
• sous graphe :
le graphe G' est un sous
graphe de G si
l'ensemble des sommets
de G' est inclus dans
l'ensemble des sommets
de G, et si l'ensemble des
arcs de G' est égal au
sous-ensemble des arcs
de G reliant entre eux
tous les sommets de G’ ;
on a donc retiré de G
certains sommets, et tous
les arcs adjacents à ces
sommets.
a
d
b
e
c
Graphe G
Graphe G’a
d
b
e
g
f
h
a
d
b
e
g
f
h

17. Définition : sous ensemble stable
• Soit un graphe G, et F
un sous-ensemble de
l’ensemble des
sommets S.
On dit que F est un
sous ensemble stable
de S s’il n’existe
aucun arc du graphe G
reliant deux sommets
de F.
a
d
b
e
c
Graphe G
a d h
forme un sous ensemble stable
a
d
g
f
h
a
d
h

18. Définition : successeur dans un graphe
orienté
Dans un graphe orienté,
pour un arc (x;y) donné,
on dit que
y est le successeur de x
x est le prédécesseur de y
t
y
x
z

19. Définition : matrice associée à un graphe
Pour le traitement
informatique, tout graphe
possède une matrice
booléenne
(i.e avec des 0 et des 1 seulement)
associée : chaque ligne
indique les successeurs
par un 1, et l’absence de
successeur par un 0.
a
d
b
c
0 1 0 0
1 0 1 1
0 1 0 1
0 1 1 0
c
b d
c est en relation avec b et d
mais pas en relation avec a
a

20. matrice associée à un graphe non orienté
Lorsque le graphe est non
orienté, la matrice
associée est symétrique
par rapport à la diagonale.
Lorsqu’il n’y a pas de
boucle, il n’y a que des
zéros sur la diagonale.
a
d
b
c
0 1 0 0
1 0 1 1
0 1 0 1
0 1 1 0
c
b
c est en relation avec b et
b est en relation avec c

21. matrice associée à un graphe orienté
Lorsque le graphe est
orienté, la matrice n’est
pas forcément
symétrique.
Lorsqu’il n’y a pas de
boucle, il n’y a que des
zéros sur la diagonale.
a
d
b
c
0 0 0 0
1 0 0 1
0 1 0 0
0 0 1 0
b
a d
b est en relation avec a et d
mais a n’est pas en relation avec b
b
a

22. Graphe probabiliste
Pour décrire des
phénomènes aléatoires
se répétant, on peut
utiliser un graphe et la
matrice qui lui est
associée.
On parle alors de
graphe probabiliste (car
en lien avec des calculs
de probabilités).
a
2/3 1/3
3/5 2/5b
a b
a
b
1/3
2/5
3/5
2/3
La proba de passer de l’état a à l’état b est 1/3