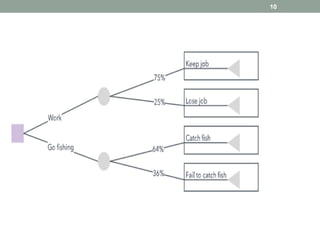
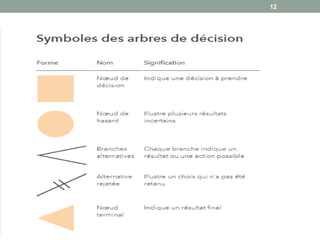
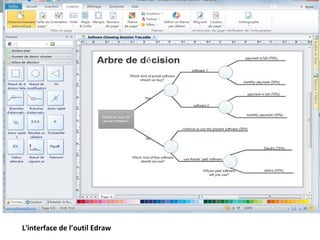
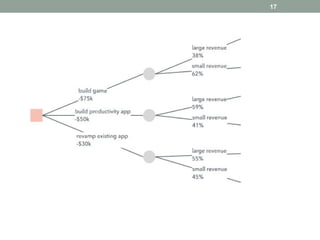
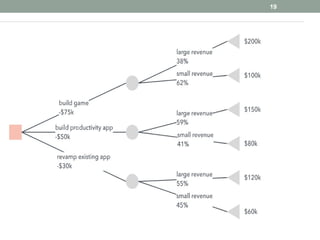
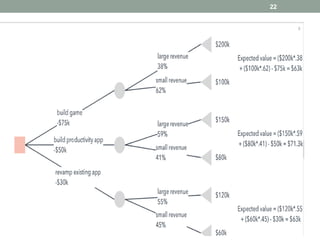
Les arbres de décision sont des outils d'analyse utilisés en business intelligence pour évaluer les choix possibles en fonction de leurs coûts et bénéfices. Ils se composent de différents types de nœuds (décision, hasard, terminal) et sont utilisés pour la classification et la régression. Les arbres de décision sont appréciés pour leur simplicité et leur capacité à visualiser des options, bien qu'ils présentent des inconvénients liés à la complexité et au surapprentissage.

1. Les arbres de décisions
Realisé par : Chaabene Mariem
Encadré par : Mourad Tissaoui
11

2. Le plan
• Introduction
• Origines
• Définition
• Comment dessiner un arbre de décision ?
• Les avantages
• Inconvénients
• Qu’est-ce que sont les arbres de classification et les arbres de régression ?
• Arbres de classification et Arbres de classification et algorithme CART
• Le pré-élagage
• Le post-élagage
• conclusion
•
•
•
•
•
22

3. Introduction
Depuis déjà quelques années, la Business Intelligence
occupe une place de choix dans la liste des priorités des
entreprises.
Les techniques et les méthodes d'analyse des données de
l'entreprise améliorent la prise de décision. Et dans ce
contexte on site : Les incontournables arbre de décision,
les Arbre de décision, outil d'analyse de la Business
Intelligence
3

4. Origines
• Ces méthodes ont pris essentiellement leur essor dans le
cadre des approches d'apprentissage automatique
(machine learning) en Intelligence Artificielle.
• Particularités (de l'I.A. en général): met l'accent sur sur la
convivialité et l'intelligibilité (ou la lisibilité) des résultats =>
en classification supervisée: sortie de résultats sous la
forme de règles logiques de classification: "SI tel ensemble
de conditions sur telles variables est satis fait ALORS le cas
appartient à telle classe".
=> résultats plus facilement interprétables et donc exploitables
=> communication plus aisée avec les spécialistes du
domaine traité.
44

5. • Ex d'algorithme: ID3 (Inductive Decision Tree) et son
successeur C4.5, CART (Classification and Regression
Tree), CHAID (Chi-Square Automatic Interaction
Detection), QUEST (Quick, Unbiased, Efficient Statistical
Trees).
5

6. 6

7. Définition
• Un arbre de décision est un schéma représentant les
résultats possibles d'une série de choix interconnectés.
• Il permet à une personne ou une organisation d'évaluer
différentes actions possibles en fonction de leur coût,
leur probabilité et leurs bénéfices.
• Il peut être utilisé pour alimenter une discussion informelle
ou pour générer un algorithme qui détermine le meilleur
choix de façon mathématique.
77

8. Définition
• Un arbre de décision commence généralement par un
nœud d'où découlent plusieurs résultats possibles.
Chacun de ces résultats mène à d'autres nœuds, d'où
émanent d'autres possibilités.
88

9. Comment dessiner un arbre de décision ?
Les noeuds
• Il existe trois types de nœuds différents : des nœuds de
hasard, des nœuds de décision et des nœuds terminaux.
• Un nœud de hasard: représenté par un cercle, montre les
probabilités de certains résultats.
• Un nœud de décision: représenté par un carré, illustre une
décision à prendre,
• un nœud terminal: le résultat final d'un chemin de décision
99

10. 1010

11. • Les arbres de décision peuvent aussi être dessinés avec
des symboles d’organigramme .
• Certaines personnes jugent que ce procédé génère des
schémas plus simples à lire et à comprendre.
•
1111

12. 1212

13. Comment dessiner un arbre de décision ?
• Pour dessiner un arbre de décision, choisissez d'abord un
support. Vous pouvez le dessiner à main levée sur du
papier ou sur un tableau blanc, ou vous pouvez utiliser
un logiciel d'arbres de décision spécialisé.
• Exemple : Sipina ,Edraw
•
1313

14. L'interface de l’outil Edraw
14

15. Dans tous les cas, voici les étapes à
suivre :• Commencez par la décision principal Dessinez une
petite boîte pour la représenter, puis dessinez une ligne
partant de la boîte vers la droite pour chaque solution ou
action possible. Étiquetez-les.
•
1515

16. • Ajoutez des nœuds de hasard et de décision pour
développer l'arborescence comme suit :
• Si une autre décision est nécessaire, dessinez une autre
boîte.
• Si le résultat est incertain, dessinez un cercle (les cercles
représentent les nœuds de hasard).
• Si le problème est résolu, n'ajoutez rien.
1616

17. 1717

18. • 3. Continuez à développer l'arbre jusqu'à ce que
chaque ligne débouche sur un nœud terminal,
indiquant qu'il n'y a plus de choix à faire ni de résultats
possibles à prendre en considération. Ensuite, assignez
une valeur à chaque résultat possible. Cela peut être un
score abstrait ou une somme d'argent. Ajoutez des
triangles pour signaler les nœuds terminaux.
1818

19. 1919

20. •
• Une fois l'arbre de décision terminé, vous pouvez
commencer à analyser la décision qui s'impose à vous.
2020

21. Exemple d'analyse d'un arbre de
décision• En calculant l'utilité ou la valeur attendue de chaque choix
de l'arbre, vous pouvez minimiser les risques et
optimiser les chances de parvenir à un résultat
satisfaisant.
• Pour calculer l'utilité espérée d'un choix, il vous suffit de
soustraire le coût de cette décision des bénéfices
attendus.
• Les bénéfices attendus sont égaux à la valeur totale de
tous les résultats qui pourraient être dus à ce choix,
chaque valeur étant multipliée par la probabilité de
réalisation du choix qui lui est associé. Voici comment
nous calculerions ces valeurs pour l'exemple ci-dessus :
•
2121

22. 2222

23. • Lors de l'identification du résultat le plus souhaitable, il est
important de prendre en compte les préférences du
décideur.
• Par exemple, certains peuvent préférer des options à
faible risque tandis que d'autres sont prêts à prendre
des risques pour gagner davantage.
•
2323

24. les Avantages
• La popularité des arbres de décision se justifie par les raisons suivantes :
• Ils sont faciles à comprendre.
• De nouvelles options peuvent être ajoutées aux arbres existants.
• Ils permettent de sélectionner l'option la plus appropriée parmi plusieurs.
• Il est facile de les associer à d'autres outils de prise de décision.
•
2424

25. Les inconvénients
• L'apprentissage de l'arbre de décision optimal est NP-
complet concernant plusieurs aspects de l'optimalité
• L'apprentissage par arbre de décision peut amener des
arbres de décision très complexes, qui généralisent mal
l'ensemble d'apprentissage (il s'agit du problème
de surapprentissage On utilise des procédures
d'élagage pour contourner ce problème
25

26. Les inconvénients
• Certains concepts sont difficiles à exprimer à l'aide
d'arbres de décision (comme XOR ou la Parité). Pour
résoudre ce problème, plusieurs moyens existent, tels
que la proportionnalisation, ou l'utilisation d'algorithmes
d'apprentissage utilisant des représentations plus
expressives (par exemple la programmation logique
inductive).
•
26

27. Critère de segmentation
• Usuellement, les algorithmes pour construire les arbres
de décision sont construits en divisant l'arbre du sommet
vers les feuilles en choisissant à chaque étape une
variable d'entrée qui réalise le meilleur partage de
l'ensemble d'objets, comme décrit précédemment. Pour
choisir la variable de séparation sur un nœud, les
algorithmes testent les différentes variables d'entrée
possibles et sélectionnent celle qui maximise un critère
donné.
2727

28. Qu’est-ce que sont les arbres de classification,
et les arbres de régression ?
• Les arbres de classification et de régression (parfois
aussi appelés arbres de segmentation ou de décision)
sont des méthodes qui permettent d’obtenir des
modèles à la fois explicatifs et prédictifs.
• Parmi leurs avantages on notera d’une part leur simplicité
du fait de la visualisation sous forme d’arbres, d’autre
part la possibilité d’obtenir des règles en langage
naturel.
28

29. Les arbres de classification et de
régression
• On distingue notamment deux cas d’utilisation de ces
modèles :
• on utilise les arbres de classification pour expliquer et/ou
prédire l’appartenance d’objets (observations, individus)
à une classe (ou modalité ou catégorie) d’une variable
qualitative, sur la base de variables explicatives
quantitatives et/ou qualitatives.
29

30. Les arbres de classification et de
régression• Dans le cas des arbres de classification, il s'agit d'un problème
de classification automatique .
• Le critère d’évaluation des partitions caractérise l'homogénéité
(ou le gain en homogénéité) des sous-ensembles obtenus par
division de l'ensemble.
• Ces métriques sont appliquées à chaque sous-ensemble candidat
et les résultats sont combinés (par exemple, moyennés) pour
produire une mesure de la qualité de la séparation
• Il existe un grand nombre de critères de ce type, les plus utilisés
sont l’Entropie de Shanon, le coefficient de GINI et leurs
variantes.
•
30

31. 31
•
•
•
•

32. • Définition de la régression
• La régression est un ensemble de méthodes statistiques
très utilisées pour analyser la relation d'une variable par
rapport à une ou plusieurs autres.
•
• on utilise les arbres de régression pour expliquer et/ou
prédire les valeurs prise par une variable dépendante
quantitative, en fonction de variables explicatives
quantitatives et/ou qualitatives.
•
32

33. Le pré-élagage
• La première stratégie utilisable pour éviter un
surapprentissage des arbres de décision consiste à
proposer des critères d’arrêt lors de la phase
d’expansion.
33

34. Le post-élagage
• La seconde stratégie consiste à construire l’arbre en deux
temps : on produit d'abord l’arbre dont les feuilles sont le
plus homogènes possibles dans une phase
d’expansion,
• en utilisant une première fraction de l’échantillon de
données (échantillon d’apprentissage à ne pas
confondre avec la totalité de l’échantillon, appelé en
anglais growing set pour lever l'ambiguïté), puis on
réduit l’arbre, en s’appuyant sur une autre fraction des
données de manière à optimiser les performances de
l’arbre, c’est la phase de post-élagage
34

35. CONCLUSION
• Les arbres de décision sont largement utilisés pour aider
à faire de bons choix dans de nombreuses disciplines
différentes, y compris le diagnostic médical, le science
cognitive, l'intelligence artificielle, la théorie du
programme, l'ingénierie et l'exploration de données.
35

36. webographie
• https://www.google.tn/search?q=Un+arbre+de+décision+comm
:
•
3636

37. 37