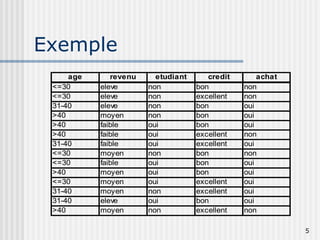
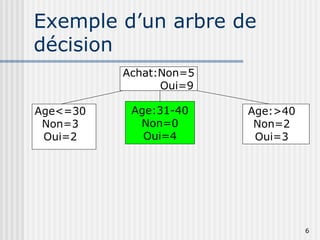
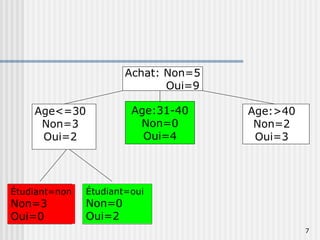
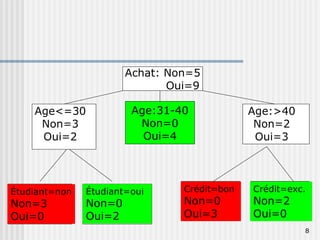
Les arbres de décision sont des outils utilisés pour prédire une variable cible à partir de plusieurs variables explicatives en divisant les données en sous-groupes. Ils permettent de générer des règles simples pour la segmentation de la population et l'identification des variables discriminantes. Des algorithmes comme CHAID et CART sont couramment utilisés pour construire ces arbres, avec des conditions spécifiques pour leur croissance et leur élagage.

1. 1
Les Arbres de décision ou
régression (exemple )

2. 2
Contexte
 Supposons que nous désirons comprendre
ou expliquer le profil des gens qui achète
un ordinateur. Pour ce faire, nous
considérons les variables suivantes:
 Âge, revenu, étudiant ou non,cote de crédit
 Quel raisonnement ou démarche fait-on
naturellement pour établir ce profil?

3. 3
Les arbres de décision
 Les arbres de décision sont utilisés pour la
prédiction ou l’explication d’une variable cible (Y)
(target variable, variable dépendante) à partir
d’un ensemble de variable explicatives (X) (input
variables, variables indépendantes)
 Le principe des arbres de décision est de diviser
l’ensemble des données d’apprentissage
successivement en sous-groupes, selon les
valeurs prises par les variables explicatives qui à
chaque étape discrimine le mieux la variable
cible.

4. 4
 Le résultat est un ensemble de
règles simples qui permettent de
réaliser des prévisions, de
segmenter la population ou
d’identifier qu’elles sont les variables
qui discriminent le plus la variable
cible.

5. 5
Exemple
age revenu etudiant credit achat
<=30 eleve non bon non
<=30 eleve non excellent non
31-40 eleve non bon oui
>40 moyen non bon oui
>40 faible oui bon oui
>40 faible oui excellent non
31-40 faible oui excellent oui
<=30 moyen non bon non
<=30 faible oui bon oui
>40 moyen oui bon oui
<=30 moyen oui excellent oui
31-40 moyen non excellent oui
31-40 eleve oui bon oui
>40 moyen non excellent non

6. 6
Exemple d’un arbre de
décision
Achat:Non=5
Oui=9
Age:31-40
Non=0
Oui=4
Age:>40
Non=2
Oui=3
Age<=30
Non=3
Oui=2

7. 7
Achat: Non=5
Oui=9
Age:31-40
Non=0
Oui=4
Age:>40
Non=2
Oui=3
Age<=30
Non=3
Oui=2
Étudiant=non
Non=3
Oui=0
Étudiant=oui
Non=0
Oui=2

8. 8
Achat: Non=5
Oui=9
Age:31-40
Non=0
Oui=4
Age:>40
Non=2
Oui=3
Age<=30
Non=3
Oui=2
Étudiant=non
Non=3
Oui=0
Étudiant=oui
Non=0
Oui=2
Crédit=bon
Non=0
Oui=3
Crédit=exc.
Non=2
Oui=0

9. 9
Algorithmes et logiciels les plus
répandus pour construire les arbres de
décision:
 CHAID  Chi-Square Automatic
Interaction Detection (1975)
 CART  Classification And
Regression Trees (Breiman et al.,
1984)
 Knowledge seeker

10. 10
Algorithme
1) Pour chaque nœud de l’arbre:
 Pour chacune des variables explicatives X, jumelage
des modalités à partir du test du chi-carré.
 Après le jumelage des modalités pour chaque X,
Sélection de la variable X la plus fortement lié avec la
variable cible Y, c.-à-d. p-value du test du chi-carré le
plus petit.
1) Pour chaque nœud fils suivant, reprise des étapes a) et b)
2) Le processus s’arrête lorsque à tous les nœuds de l’arbre,
les tests du chi-deux entre les variables X et Y sont tous
non significatifs c.-à-d. p-value > α

11. 11
Conditions d’arrêt de la
croissance de l’arbre
 Développement de l’arbre complet:
 toutes les observations dans le nœud
appartiennent à la même classe de la
variable cible;
 il n’y a plus de variables explicatives X
à considérer pour poursuivre la
croissance de l’arbre;
 trop peu d’observations dans le nœud
pour poursuivre.

12. 12
L’élagage (pruning)
 L’arbre complet est le meilleur, en terme
de taux d’erreur, pour prédire la variable
cible, pour l’ensemble des données
d’apprentissage!
 Qu’en est-il pour un nouvel ensemble de
données?
 L’arbre complet n’est probablement pas la
meilleure solution!
 Évaluer les sous-arbres:
 Utiliser un échantillon de validation.
 Utiliser la validation croisé.

13. 13
Construire un arbre à partir
d’excel
 Nous pouvons générer un arbre
manuellement à partir d’excel:
 On utiliser la fonction ‘pivot tables’ pour
obtenir nous comptes
 On utilise les utilitaire graphiques
d’excel.
 Exemple.