Ce document présente plusieurs exercices d'analyse de fonctions mathématiques, incluant l'étude des variations, la détermination des tangentes et des points d'intersection entre différentes courbes. Chaque exercice aborde des concepts comme les dérivées, les propriétés des fonctions (parité, asymptotes) et des représentations graphiques. La méthode inclut des étapes de calcul et des vérifications graphiques à l'aide de calculatrices.

1. ETUDE DES FONCTION
EXERCICE 1
Soit f la fonction définie par f (x) = x3 - x² + 1 et (C) la courbe représentative de f dans un repère
orthonormal (O, , ).
1. Étudier les variations de f.
2. On appelle A le point de (C) dont l'abscisse est 2.
a) Déterminer une équation de la tangente (D) à (C) en A. (Écrire cette équation sous la forme y
= t(x)).
b) On pose d(x) = f(x) - t(x). Vérifier que d(x) = x(x - 2)².
c) Préciser la position de la courbe (C) par rapport à la tangente (D).
d) Dessiner (C) et (D).
EXERCICE 2
Soient (C) et (C') les courbes d'équations respectives y = x 3 - 2x + 3 et y = 2x² - 3x + 3.
1. Déterminer les coordonnées des points communs à (C) et (C').
2. Déterminer les équations des tangentes à (C) et (C') en chacun de leurs points communs.
3. Étudier les variations des fonctions : x x3 - 2x + 3 et x 2x² - 3x + 3.
4. Dessiner (C) et (C') dans le repère (O, , ).
EXERCICE 3
Soit f la fonction définie sur R-{2} par : f (x) = et (C) sa courbe représentative dans
un plan muni d'un repère orthonormal. Déterminez a, b, c pour que (C) ait les propriétés suivantes
:
(C) passe par le point A(0 ; 5)
la tangente à (C) au point A est parallèle à l'axe des abscisses ;
la tangente à (C) au point B d'abscisse 1 a pour coefficient directeur -3.
Étudier les variations de la fonction f ainsi obtenue.
Tracer (C).

2. EXERCICE 4
On considère la fonction f définie sur par : et C sa courbe représentative
dans un repère orthonormal d'unité 1 cm.
1. a) Déterminer les réels et tels que, pour tout réel : .
b) Montrer que f est impaire. Que peut-on en déduire pour la courbe C ?
2. Soit la dérivée de .
a) Montrer que .
b) Étudier les variations de .
3. Préciser une équation de la tangente T à la courbe C à l'origine.
4. Soit D la droite d'équation .
a) Étudier la position de C relativement à la droite D.
b) Montrer que, pour tout non nul : .
En déduire la limite de quand tend vers + . Que peut-on en conclure pour la courbe C
?
5. Tracer D, T et C sur un même graphique. (On précisera les points d'intersection de la courbe C
avec l'axe des abscisses).
EXERCICE 5
Etude d'une fonction définie sur [-2; 2] par: f (x) = x3 + 2x et C sa courbe représentative dans le plan
muni du repère orthogonal (O, , ) (unités: 3 cm pour 1 sur (O, ) et 0,5 cm pour 1 sur (O, )).
1. f est-elle impaire?
2. Étudier les variations de f.
3. Déterminer une équation de la tangente T à C au point d'abscisse 0.
4. Déduire de l'étude du signe de l'expression f (x) - 2x, la position de la courbe C par rapport à la
tangente T, lorsque x varie dans [-2, 2].
5. Construire C et T après avoir déterminé les coordonnées d'une dizaine de points à l'aide d'une
calculatrice programmable.

3. COURIGER
EXERCICE 1
1. Soit définie sur .
est dérivable sur .
On étudie le signe de puis on en déduit les variations de :
Donc
Avec :
2. Soit A(2; ) (C).
2. a) est dérivable en 2 donc (D) existe bien.
Ainsi, (D) a pour équation :
Donc
2. b) Posons
2. c) Position relative de (C) par rapport à (D).
Il faut étudier le signe de la différence des deux fonctions et soit, étudier le signe
de .
Ainsi,
sur ] ;0[:

4. sur ]0;2[ ]2; [:
2. d)
EXERCICE 2
Soit (C) courbe d'équation . Posons définie sur .
est dérivable sur donc .
Soit (C') courbe d'équation . Posons définie sur .
est dérivable sur donc .
1. Déterminer les coordonnées des points communs à (C) et (C') revient à déterminer les solutions
de l'équation :
Ainsi, et (C) et (C') ont deux points communs et d'abscisse respective 0 et 1
Calcul de leur ordonnée :

5. Les points communs à (C) et (C') sont donc et .
2. Tangente à (C) en :
est dérivable en 0 donc la tangente existe bien
; ;
.
Tangente à (C') en :
est dérivable en 0 donc la tangente existe bien.
; ; [nl
Tangente à (C) en :
est dérivable en 1 donc la tangente existe bien.
; ;
Tangente à (C') en :
est dérivable en 1 donc la tangente existe bien.
; ;
3. Étude des variations de :
Soit définie sur .
est dérivable sur .
On cherche les solutions de l'équation :
ou
Étude des variations de :
Soit définie sur .
est dérivable sur .
On cherche les solutions de l'équation :

6. EXERCICE 3
Soit définie sur .
C passe par le point A(0;5) :
La tangente à (C) au point A(0;5) est parallèle à l'axe des abscisses :
Posons et
est dérivable sur .

7. Donc,
La tangente à (C) au point B(1; ) a pour coefficient directeur -3 :
Ainsi, on a déterminé , et pour que (C) réponde aux trois propriétés proposées. Il est possible
de vérifier que l'on ne s'est pas trompé en affichant le graphique à sur la calculatrice et en vérifiant
les 3 propriétés graphiquement.
Soit définie sur
est dérivable sur Df

8. EXERCICE 4
1. a) Si
Par identification :
Donc
1. b) Soit et Df=
Df symétrique par rapport à 0
Donc est impaire et sa courbe représentative C est symétrique par rapport à l'origine du repère.
2. a) Soit et Df=
Posons
et
est dérivable sur
2. b) Soit

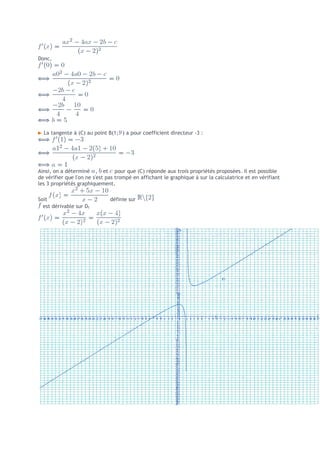
9. 3. ; ;
4. a) Soit D la droite d'équation
sur ] ;0[ :
sur ]0; [:
Il suffit de faire la différence entre C et D puis étudier le signe de l'expression ainsi obtenue.
C est en dessous de D sur ]- ;0[
C est au dessus de D sur ]0;+ [
4. b)
La limite de est nulle
D'ou la droite d'equation est un asymptote de Cf
5.

10. EXERCICE 5
Soit et Df=[-2;2]
1.
Df est symétrique par rapport à 0
Donc est une fonction impaire.
2. est dérivable sur [-2;2]
3. Équation de la tangente T à C au point d'abscisse 0.
; ;
4.

11. sur]-2;0[ :
sur]0;-2[ :
5.