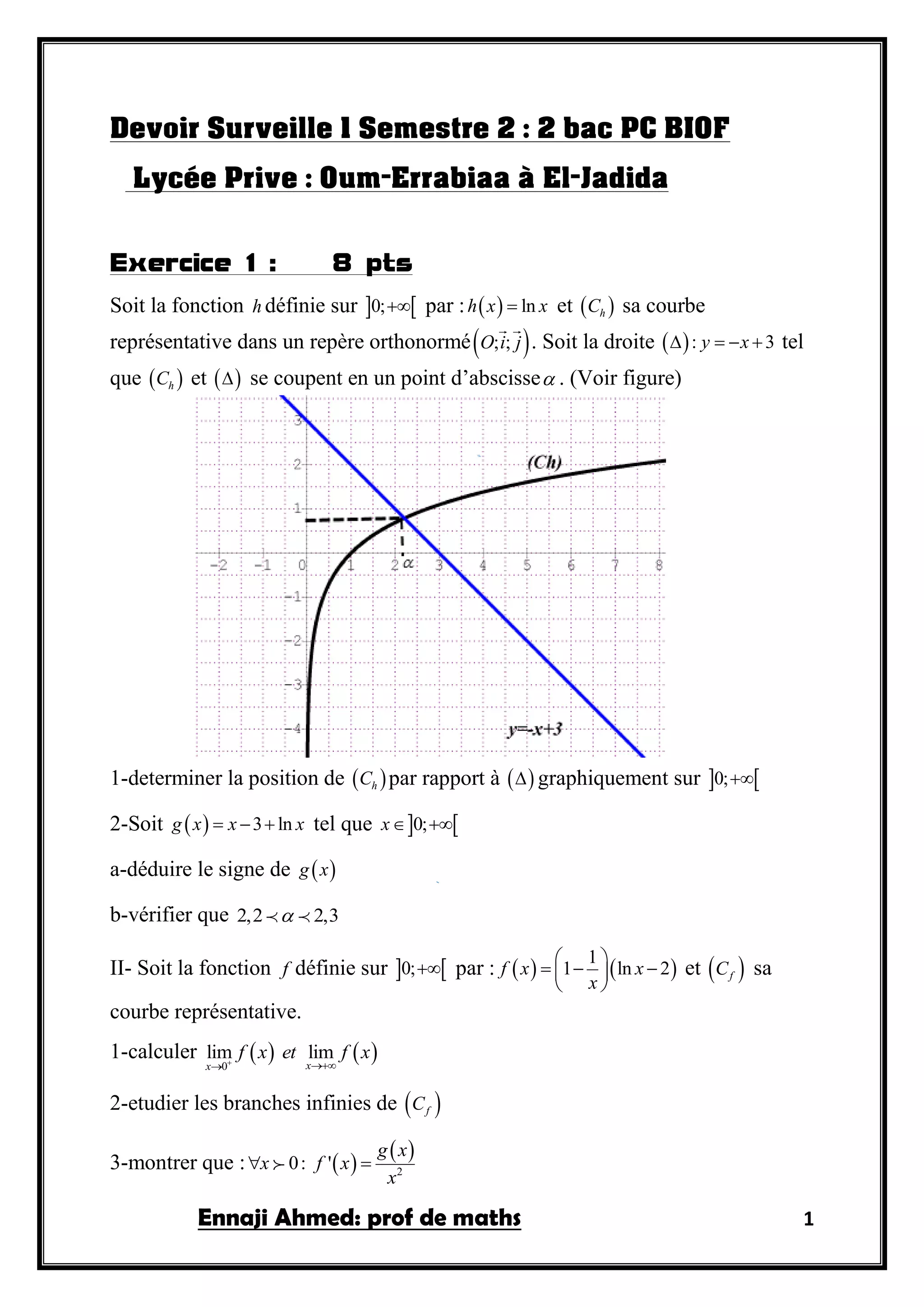
Le document présente un devoir de mathématiques comprenant plusieurs exercices sur des fonctions, des dérivées et des intégrales, ainsi que des équations différentielles. Chaque exercice contient des questions spécifiques qui nécessitent des calculs, des représentations graphiques et des analyses des comportements des fonctions. Le travail est destiné à des élèves de lycée dans un contexte académique de maths avancées.

1. Ennaji Ahmed: prof de maths 1
Devoir Surveille 1 Semestre 2 : 2 bac PC BIOF
Lycée Prive : Oum-Errabiaa à El-Jadida
Exercice 1 : 8 pts
Soit la fonction h définie sur  0; par :   lnh x x et  hC sa courbe
représentative dans un repère orthonormé ; ;O i j . Soit la droite  : 3y x    tel
que  hC et   se coupent en un point d’abscisse . (Voir figure)
1-determiner la position de  hC par rapport à   graphiquement sur  0;
2-Soit   3 lng x x x   tel que  0;x 
a-déduire le signe de  g x
b-vérifier que 2,2 2,3
II- Soit la fonction f définie sur  0; par :    
1
1 ln 2f x x
x
 
   
 
et  fC sa
courbe représentative.
1-calculer    0
lim lim
xx
f x et f x

2-etudier les branches infinies de  fC
3-montrer que :  
 
2
0: '
g x
x f x
x
 

2. Ennaji Ahmed: prof de maths 2
4-donner le tableau de variation de f
5-montrer que :  
 2
1
f




  en déduire un encadrement de  f 
6-etudier la position de  fC avec l’axe des abscisses et construire  fC sur
l’intervalle 2
0;e  
III-Soit F la primitive de f sur  0; tel que :  1 3F  
1-montrer que la courbe de la fonction F admet deux tangentes parallèles à l’axe
des abscisses en deux points dont on déterminera leurs abscisses.
2-montrer que la fonction : lnx x x x est une primitive de la fonction   lnh x x
3-endeduire l’expression de F(x).
Exercice 2 : 6pts
1-calculer
 
1 2
40 1
2
;
1 1
x
x
e
dx dx
x e 
 
2-montrer que  
2
3 4 5 1
2 : 3 2
2 2
x x
x IR x
x x
 
      
 
et calculer :
2
3
1
3 4 5
2
x x
dx
x
  
 
 

3-par la méthode d’intégration par parties, calculer  
2
3
1
lnx x dx
Exercice 3 : 6 pts
1-Résoudre l’équation différentielle suivante :
 : " 2 ' 5 0E y y y  
2-determiner la fonction g solution de l’équation différentielle (E) qui vérifie :
   0 1 ' 0 1g et g 
3-en déduire que :  0
1
cos 2
5
x e
e x

 
