Ce document traite de la fonction exponentielle, en présentant sa définition, ses propriétés, et ses dérivées. Il inclut également des exemples d'application ainsi que des exercices pour illustrer les concepts abordés. Les propriétés de la fonction exponentielle ainsi que ses liens avec le logarithme népérien sont également expliqués.

1. 2éme Bac PC-SVT
www.etude-generale.com
www.etude-generale.com
Matière : Mathématiques
Professeur : Yahya MATIOUI
Fonction exponentielle
1 Dé…nition et résultats
Dé…nition 1 La fonction réciproque de la fonction ln s’
appelle la fonction
exponentielle est notée exp; et
exp R ! ]0; +1[
x 7 ! exp x
avec exp(0) = 1:
Notation nouvelle :
exp x = exp(x 1) = (exp(1))x
= ex
: On note pour tout x réel, on a
exp x = ex
Résultats
La fonction exponentielle est dé…nie sur l’
ensemble R:
La fonction exponentielle est continue et dérivable sur R; et on a : (ex
)0
=
ex
:
La fonction exponentielle est strictement croissante sur R:
(8x 2 R); ex
0
1

2. 2 Propriétés
Propriété 2 Pour tous les nombres réels x et y, et l’
entier naturel n; on a :
1. e0
= 1 et e1
w 2; 718
2. ex+y
= ex
ey
3. ex y
= ex
ey
4. e x
= 1
ex
5. (ex
)n
= enx
6. ex
6= 0
Remarque 3 (Lien avec le logarithme népérien)
1. 8x 2 R; ln(ex
) = x:
2. 8x 2 ]0; +1[ ; eln x
= x:
Propriété 4 1. (8x 2 R)(8a 2 ]0; +1[); ex
= a () x = ln a
2. 8x; y 2 R; ex
= ey
() x = y
3. 8x; y 2 R; ex
ey
() x y
Exemple 5 Résoudre dans l’
ensemble R l’
équation (E) : e2x2+3
= e7x
:
e2x2+3
= e7x
() 2x2
+ 3 = 7x () 2x2
7x + 3 = 0
Calculons le discriminant de l’
équation du second degré.
= 49 24 = 25 0
x1 =
b +
p
2a
=
7 + 5
4
= 3 et x2 =
b
p
2a
=
7 5
4
=
1
2
donc
S =
1
2
; 3
Résoudre dans l’
ensemble R l’
inéquation (I) : e3x
ex+6
:
e3x
ex+6
() 3x x + 6 () x 3
donc
S = ] 1; 3[
2

3. 3 Limites de références
Propriété 6 Soit n 2 N:
1. limx !+1 ex
= +1:
2. limx !+1
ex
x
= +1 et limx !+1
ex
xn = +1:
3. limx ! 1 ex
= 0:
4. limx ! 1 xex
= 0 et limx ! 1 xn
ex
= 0:
5. limx !0
ex 1
x
= 1:
Exemple 7 Calculer les limites suivantes :
lim
x !+1
(x + e 3x
) ; lim
x ! 1
e1 1
x et lim
x !+1
ex
+ x
ex x2
Calculons la limite : limx !+1(x + e 3x
):
lim
x !+1
(x + e 3x
) = +1 + 0 = +1
Car : lim
x !+1
e 3x
= 0
Calculons la limite : limx ! 1 e1 1
x :
lim
x ! 1
e1 1
x = e
Car : lim
x ! 1
(1
1
x
) = 1
Calculons la limite : limx !+1
ex+x
ex x2
lim
x !+1
ex
+ x
ex x2
= lim
x !+1
ex
(1 + x
ex )
ex(1 x2
ex )
= lim
x !+1
1 + x
ex
1 x2
ex
Comme : lim
x !+1
x
ex
= lim
x !+1
1
ex
x
= 0: car lim
x !+1
ex
x
= +1
et lim
x !+1
x2
ex
= lim
x !+1
1
ex
x2
= 0: car lim
x !+1
ex
x2
= +1
alors
lim
x !+1
ex
+ x
ex x2
= 1
3

4. 4 Courbe représentative de la fonction expo-
nentielle
D’
après les résultats obtenus dans le premier paragraphe, on déduit le tableau
de variations de la fonction exponentielle ainsi sa courbe représentative dans
un repère orthonormé (O;
!
i ;
!
j ) :
f R ! ]0; +1[
x 7 ! ex
La courbe représentative de la fonction exponentielle.
2 3
-1
-2
-3
-4
-5
2
3
4
5
0 1
1
x
y
4

5. 5 Fonction de la forme x 7 ! eu(x)
5.1 Dérivée de la fonction eu
:
Propriété 8 Soit la fonction u dérivable sur un intervalle I, alors la fonc-
tion eu
est dérivable sur I et :
(eu
)0
= u0
eu
Exemple 9 Soient f et g deux fonctions dé…nies sur R par : f(x) = e2x 1
et g(x) = e x2
:
f et g sont dérivable sur R, donc f0
(x) = 2e2x 1
et g0
(x) = 2xe x2
:
Propriété 10 Soit u une fonction dérivable sur un intervalle I: Les fonc-
tions u et eu
ont le même sens de variations.
5.2 Primitives
Propriété 11 Soit u une fonction dérivable sur un intervalle I:
L’
ensemble des fonctions primitives de la fonction u0
eu
sur I sont les
fonctions eu
+ k avec k 2 R:
Exemple 12 On considère la fonction f dé…nie sur ] 1; +1[ par :
f(x) =
1
2
p
x + 1
e
p
x+1
La fonction f est continue sur ] 1; +1[, elle admet donc des fonctions
primitives sur ] 1; +1[ :
f est de la forme u0
eu
avec u(x) =
p
x + 1 et u0
(x) = 1
2
p
x+1
pour tout
x 2 ] 1; +1[ :
On a
f(x) = (
p
x + 1)0
e
p
x+1
donc
F(x) = e
p
x+1
+ k; (k 2 R)
5

6. 6 Exercice d’
application
Exercice 13 Soit f la fonction dé…nie sur R par :
f(x) = xe
x
2
et (Cf ) sa courbe représentative dans un repère orthonormé (O;
!
i ;
!
j ):
1. Calculer : limx !+1 f(x) et limx ! 1 f(x):
2. Calculer la dérivée de la fonction f; et dresser le tableau de variations
de la fonction f:
3. Tracer la courbe représentative de la fonction f:
Solution 14 1. La limite de la fonction f en +1:
lim
x !+1
f(x) = lim
x !+1
xe
x
2
= lim
x !+1
x
e
x
2
= lim
x !+1
2x
2
e
x
2
= lim
x !+1
2
e
x
2
x
2
= 0
car : lim
x !+1
e
x
2
x
2
= +1
La limite de la fonction f en 1:
lim
x ! 1
f(x) = lim
x ! 1
xe
x
2 = 1
car : lim
x ! 1
e
x
2 = +1 et lim
x ! 1
x = 1:
2. Justi…ons d’
abord la dérivabilité de la fonction f sur R:
La fonction f s’
écrit comme le produit de deux fonctions u et v:
u(x) = x et v(x) = e
x
2
6

7. * u est une fonction polynôme dérivable sur R:
On pose h la fonction dé…nie par : h : x 7 ! x
2
:
* h est une fonction polynôme dérivable sur R; donc la fonction v est
dérivable sur R:
On déduit que la fonction f est dérivable sur R comme le produit
de deux fonctions derivables:
Calculons f0
(x) pour tout x 2 R:
f0
(x) = (xe
x
2 )0
= e
x
2 + x (
1
2
)e
x
2
= (1
x
2
)e
x
2
Comme e
x
2 0, alors le signe de f0
(x) sur R est celui de (1 x
2
):
On dresse le tableau de variations :
3. La courbe représentative de la fonction f:
2 3 4 5 6 7
-1
-2
-3
-4
2
3
-1
-2
-3
0 1
1
x
y
7

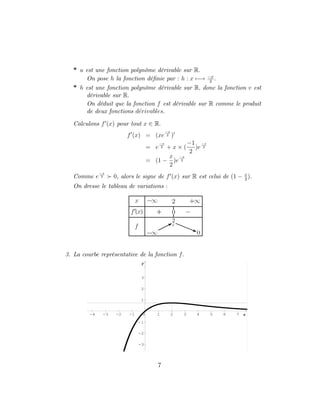
8. 7 La fonction exponentielle de base a 2 R+
7.1 Dé…nition et propriétés
Dé…nition 15 La fonction dé…nie sur R telle que x 7 ! ex ln a
s’
appelle la
fonction exponentielle de base a, notée ax
:
Propriété 16 Pour tous réels x et y, on a :
1. ax+y
= ax
ay
2. ax y
= ax
ay
3. (ax
)y
= axy
4. a x
= 1
ax :
Propriété 17 Soit a un élément de R+ n f1g :
1. (8x 2 R)(8y 2 ]0; +1[); ax
= y () x = ln y
ln a
:
2. (8x 2 R); loga(ax
) = x:
Exemple 18 Résoudre dans R l’
équation : 4x
= 18
4x
= 18 () x =
ln 18
ln 4
donc
S =
ln 18
ln 4
8 L’
étude de la fonction x 7 ! ax
Propriété 19 La fonction x 7 ! ax
est dérivable sur R et on a : (ax
)0
=
ln a ax
:
Propriété 20 1. Si a 1 alors la fonction x 7 ! ax
est strictement
croissante sur R:
2. Si 0 a 1 alors la fonction x 7 ! ax
est strictement décroissante
sur R:
8

9. 3. Si a 1 alors limx !+1 ax
= +1 et limx ! 1 ax
= 0:
4. Si 0 a 1 alors limx !+1 ax
= 0 et limx ! 1 ax
= +1:
FIN
Pr : Yahya MATIOUI
www:etude generale:com
9