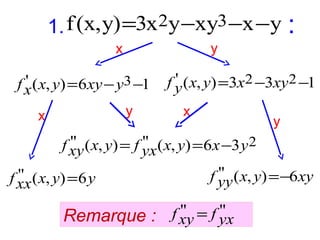
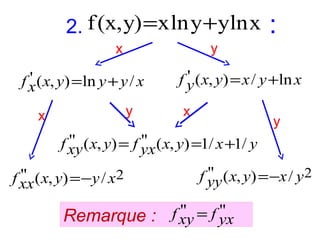
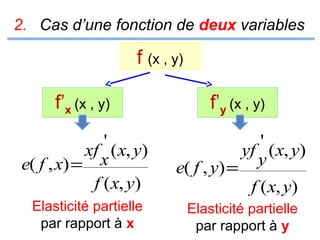
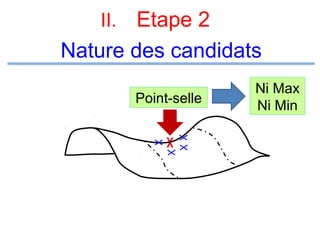
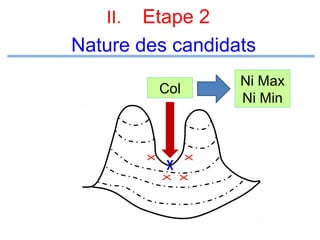
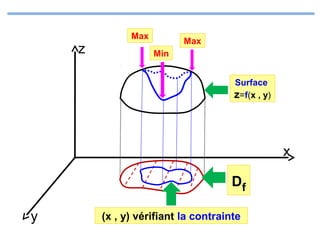
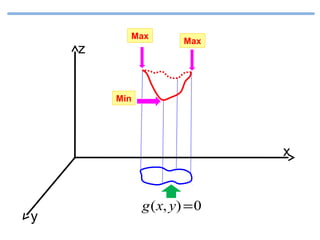
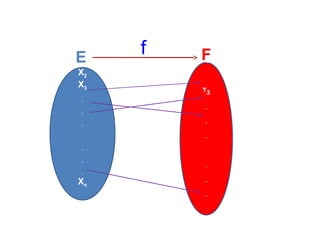
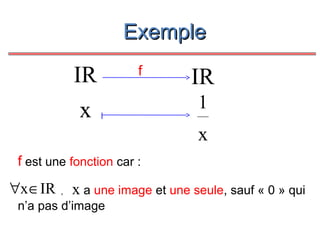
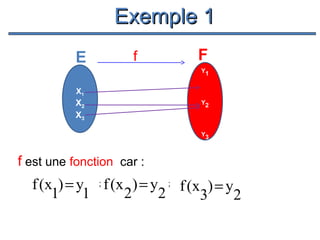
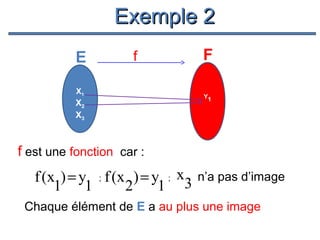
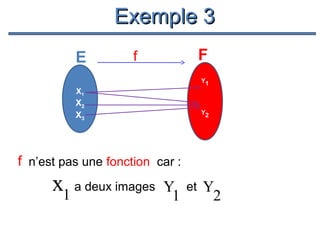
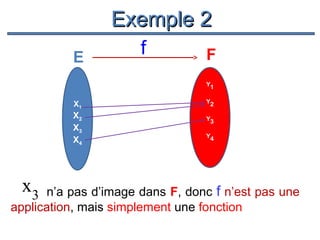
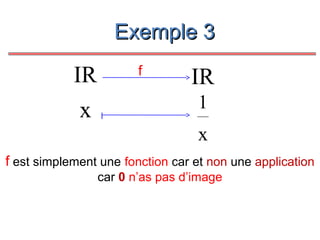
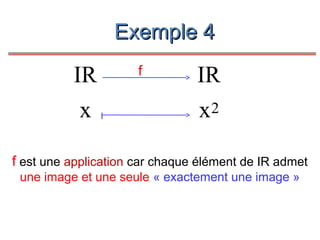
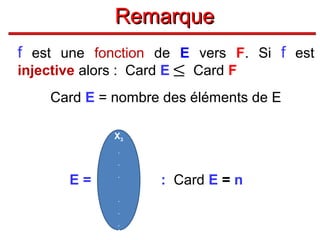
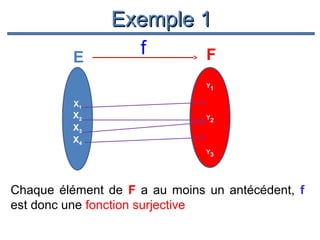
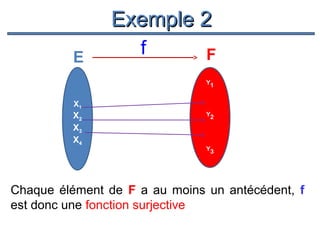
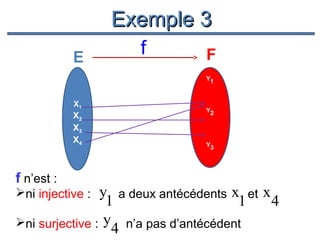
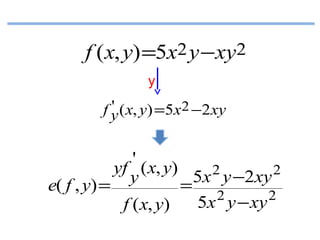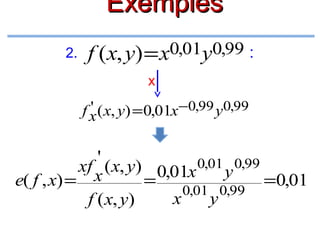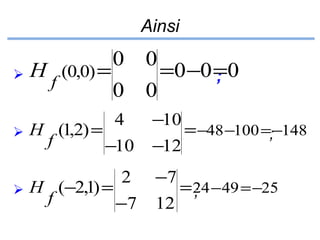Le document présente un cours de mathématiques sur l'analyse, axé sur les fonctions à une ou deux variables réelles. Il explique les notions de fonction, d'injection, de surjection, de bijection, ainsi que des exemples illustratifs, et décrit également les domaines de définition de différentes fonctions. Cette synthèse est destinée aux étudiants de l'université Hassan II pour l'année universitaire 2008/2009.

1. Université Hassan II
Faculté des Sciences Juridiques,
Économiques et Sociales de
Mohammedia
Année Universitaire 2008/2009
MATHEMATIQUES (Semestre 2)
– ANALYSE –
Professeur : M.REDOUABY

2. ANALYSE
Contenu du cours :
A.
Fonctions à une variable réelle
B.
Fonctions à deux variables réelles

3. Séance n° 1

4. A. Fonctions à une variable réelle
1.Introduction
a)
b)
c)
d)
e)
Notion de fonction
Notion d’injection
Notion de surjection
Notion de bijection
Bijection et bijection réciproque

5. a) Notion de fonction
Définition
Une fonction est une relation entre deux
ensembles E et F telle que :

Chaque élément de E (ensemble des
antécédents) a au plus une image dans F
(ensemble des images)

6. Y1
E
X
1
X2
X3
f
F
Y2
Y3
.
.
.
.
.
.
.
.
.
.
Xn
.
.
Ym

7. 
E = ensemble de départ, contient ‘n’ éléments :
X1 ; X2 ; X3 ; …. ; Xn ,
Ce sont les antécédents

F = ensemble d’arrivée, contient ‘m’ éléments :
Y1 ; Y2 ; Y3 ; …., Ym
Ce sont les images
Nous avons :
f (x1) = y1 ; f (x2) = y3 ; f (x3) = y2 ;
…….. ;
f (xn) = ym

8. Y1 est
l’image de X1 ; X1 est l’antécédent de Y1
Y3 est l’image de X2 ; X2 est l’antécédent de Y3
……
Ym est
l’image de Xn ; Xn est l’antécédent de Ym
Pour que f soit une fonction,
chaque élément de E doit avoir
au plus une image dans F

9. Exemple
IR
x
f
I
IR
1
x
f est une fonction car :
∀x∈IR
,
x a une image et une seule, sauf « 0 » qui
n’a pas d’image

10. 
Ainsi, par une fonction, un
élément de E ne peut jamais avoir
plus d’une image dans F

11. Exemple 1
E
f
F
Y1
X1
X2
X3
Y2
Y3
f est une fonction car :
f (x ) = y ; f (x ) = y ; f (x ) = y
2
2
1 1
3
2

12. Exemple 2
E
f
X1
X2
X3
F
Y1
f est une fonction car :
f ( x ) = y ; f (x ) = y ; x3
1 1
2
1
n’a pas d’image
Chaque élément de E a au plus une image

13. Exemple 3
E
F
f
Y1
X1
X2
X3
Y2
f n’est pas une fonction car :
x1 a deux images
Y
1
et
Y
2

14. Remarque Importante
Fonction et Application
Une application est une fonction particulière.
C’est une fonction telle que chaque antécédent
a exactement une image (s’il y a un antécédent
qui n’as pas d’image alors c’est simplement une
fonction et non une application)

15. Exemple 1
E
f
F
Y1
X1
X2
X3
X4
Y2
Y3
Y4
Chaque antécédent a une image et une seul, f est
donc mieux qu’une fonction, c’est une application

16. Exemple 2
E
f
F
Y1
X1
X2
X3
X4
x3
Y2
Y3
Y4
n’a pas d’image dans F, donc f n’est pas une
application, mais simplement une fonction

17. Exemple 3
IR
x
f
I
IR
1
x
f est simplement une fonction car et non une application
car 0 n’as pas d’image

18. Exemple 4
IR
x
f
I
IR
x2
f est une application car chaque élément de IR admet
une image et une seule « exactement une image »

19. b) Notion d’injection
« fonction injective »
Définition
f est une fonction de E vers F. f est dite
injective lorsque chaque élément de F a au
plus un antécédent dans E : un antécédent ou
rien

20. Exemple 1
E
f
F
Y1
X1
X2
X3
X4
Y2
Y3
Y4
Chaque élément de F a au plus un antécédent, f est
donc une fonction injective

21. Exemple 2
E
f
F
Y1
Y2
X1
X2
X3
Y3
Y4
Chaque élément de F a au plus un antécédent, f est
donc une fonction injective

22. Exemple 3
E
f
F
Y1
X1
Y2
X2
X3
X4
Y3
Y4
f n’est pas une fonction injective car :
Y1 a deux antécédents
:
x1
et
x2

23. Exemple 4
IR
x
IR
f
x2
I
f n’est pas injective car :
par exemple 1 a deux antécédents +1 et -1
.
IR
.
IR
+1
1
0
0
-1
.
.
.
.
.
f
.
.

24. Par contre
IR+
x
g
I
IR
x2
g est injective car :
 Si Y est négatif
 Si Y est positif
(Y < 0) , alors Y n’a pas d’antécédent
(Y ≥ 0) ,Y a un seul antécédent : Y

25. A retenir
f est une fonction de E vers F. f est injective si
elle vérifie :
∀x ;x ∈E
1 2
:
f (x ) =f (x ) ⇔x = x
1
2
1 2
C’est-à-dire : deux antécédents ont la même
image si et seulement si ils sont égaux

26. Remarque
f est une fonction de E vers F. Si f est
injective alors : Card E ≤ Card F
Card E = nombre des éléments de E
X1
X2
X3
.
.
E=
.
.
.
.
Xn
: Card E = n

27. Remarque
Méthode de la règle : Voir TD

28. c) Notion de surjection
« fonction surjective »
Définition
f est une fonction de E vers F. f est dite
sujective lorsque chaque élément de F a au
moins un antécédent dans E : un antécédent
ou plusieurs antécédents

29. « fonction surjective »
f est surjective si et seulement si :
∀y∈F
∃x∈E /
f (x) = y

30. Exemple 1
E
f
F
Y1
X1
X2
X3
X4
Y2
Y3
Chaque élément de F a au moins un antécédent, f
est donc une fonction surjective

31. Exemple 2
E
f
F
Y1
X1
X2
X3
X4
Y2
Y3
Chaque élément de F a au moins un antécédent, f
est donc une fonction surjective

32. Exemple 3
E
f
F
Y1
X1
X2
X3
X4
f n’est :
Y2
Y3
Y4
y a deux antécédents x et x
1
1
4
ni surjective : y n’a pas d’antécédent
4
ni injective :

33. Remarque
f est une fonction de E vers F. Si f est
surjective alors : Card E ≥ Card F
Card E = nombre des éléments de E

34. Remarque
Méthode de la règle : Voir TD

35. d) Notion de bijection
« fonction bijective »
Définition
f est une fonction bijective (ou une bijection)
de E vers F si et seulement f est une
application qui est à la fois injective et
surjective
C’est-à-dire chaque élément de E a une image
et une seule et chaque élément de F a un
antécédent et un seul

36. Exemple 1
E
f
F
Y1
X1
X2
X3
X4
f est une bijection de E vers F :
 f est injective
 f est surjective
Y2
Y3
Y4

37. Exemple 2
E
f
X1
X2
X3
X4
F
Y1
Y2
Y3
Y4
f n’est pas bijective de E vers F :
Y5
 f n’est pas surjective car y5 n’a pas d’antécédent

38. Exemple 3
E
f
F
Y1
X1
X2
X3
X4
Y2
Y3
f n’est pas une bijection de E vers F :
 f n’est pas injective
 f n’est pas surjective

39. Exemple 4
E
f
F
Y1
X1
X2
X3
X4
Y2
Y3
f n’est pas une bijection de E vers F car :
 f n’est pas une application : x3 n’a pas d’image

40. Remarque
f est une fonction de E vers F.
Si f est bijective alors :
Card E = Card F

41. e) bijection et bijection réciproque
E
f
f-1
F

42. f
E
X
1
F
Y1
X2
X3
Y2
Y3
.
.
.
.
.
.
.
.
.
.
Xn
.
f-1
x
f
f-1
Yn
y

43. bijection et bijection réciproque
Comment passer de f à f-1 et inversement :
f (x) = y ⇔f −1(y) = x

44. Ainsi si:
X
E
1
X2
X3
.
.
f
F
Y1
Y2
Y3
.
.
.
.
.
.
.
Xn
.
.
Yn

45. alors:
F
Y1
Y2
Y3
f-1
X
E
1
X2
X3
.
.
.
.
.
.
.
.
.
.
Yn
.
Xn

46. Relation fondamentale entre f et
-1
f
f
E
F
f-1
x
∀x∈E:f −1f (x) = x
f
f-1
et
y
∀y∈F:f f −1(y) = y

47. Exemple
IR+
x
IR+
f
IR+
f-1
x2
IR+
I
x
I
On a : ∀x ∈IR +
et :
∀x ∈IR +
x
f −1 f (x) = x 2 = x = x
f  f −1(x) = ( x )2 = x

48. Exemple
IR*+
x
I
IR
x
On a :
et :
f = ln
f-1 = exp
I
∀x ∈IR*+
∀x ∈IR
IR
ln x
IR*+
ex
f −1 f (x) = eln x = x
f  f −1(x) = ln ex = x

49. Séance n° 2

50. Remarque
Relation entre
la courbe de f et la courbe de sa réciproque f-1
A retenir : La courbe de f «Cf» et la courbe
de sa fonction réciproque f-1 «Cf-1» sont
symétriques par rapport à la 1ère bissectrice
(la droite d’équation y = x)

51. Y
2ème bissectrice
Y=x
1
45°
1ère bissectrice
x
1

52. Exemple
la courbe de ln « logarithme népérien » et la
courbe de sa réciproque exp « exponentielle »
sont symétriques par rapport à la droite y = x
Cexp
Y=x
Cln

53. A. Fonctions à une variable réel
2. Domaine de définition
f
IR
IR
f (x )
xI


admet une image 
D = x∈IR x



f 

= x∈IR f (x) est définie « on peut





la calculer » 

54. Exemples
1. Fonctions polynômiales :
f (x) = a n x n +....+ a1x + a 0
fonction polynômiale (ou polynôme) de degré n
Df = IR

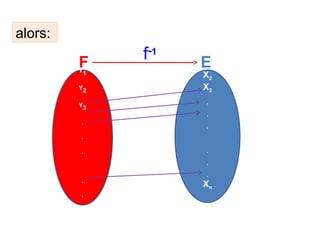
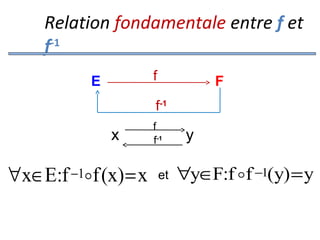
55. Fonctions polynômiales
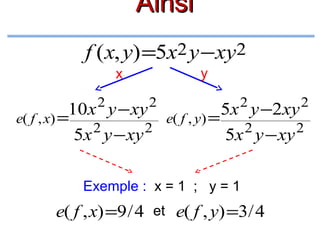
Exemples :
•
•
•
f (x) = 3x2 + x − 5
;
f (x) = 7x3 − x 2 + x +15
;
f (x) = 7x5 − x 4 + x 2 − 24
;
Pour toutes ces fonctions :∞;+∞[
D = IR =]−
f

56. Exemples
2. Fonctions rationnelles :
P(x)
f (x ) =
Q(x)
P(x) et Q(x) sont deux polynômes
Df = x∈IR Q(x) ≠ 0








57. Fonctions rationnelles
Exemple :
2x +1
f (x ) =
2
2
(x −1)(x +1)
Q(x) = 0 ⇔ (x 2 −1)(x2 +1) = 0 ⇔ x2 −1= 0
x2 +1≠ 0 , ainsi :
Car
Q(x) = 0 ⇔ x 2 =1⇔ x = ±1 ⇒ Df
= IR − ±1
Df =]− ∞;−1[∪]−1;1[∪]1;+∞[









58. Exemples
3. Fonctions racines (nèmes) :
f (x) = n u(x) ; n est un entier naturel non nul
n = 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; ……….
A retenir :
• Si n est pair :
Df = x∈IR u(x) ≥ 0
• Si n est impair :





Df = Du




59. Fonctions racines (nèmes)
Exemples :
• « racine carrée » :
f (x) = 2x +1
On doit avoir :
2x +1≥ 0 ⇔ x ≥ −1/ 2 ⇒ Df =[−1/ 2;+∞[
• « racine cubique » :
3
f (x ) =
2x +1
u(x) = 2x +1 définie quelque soit x donc
Df = Du = IR =]− ∞;+∞[

60. Exemples
4. Fonctions puissances :
f (x) = u(x)α ; α est un
nombre rationnel
α = m/n
m et n sont deux entiers naturels non nuls
On écrit :
f (x) = u(x)m / n =(u(x)m)1/ n
n u(x) m
⇒ f (x ) =

61. Fonctions puissances
Exemples :
1.
f (x) = (2x +1)4 / 5 ici α = 4 / 5
5
On a : f (x) =
(2x +1)
4
; racine impaire,
on regarde alors le domaine de définition de
(2x +1)4
(2x +1)4
:
est une fonction polynômiale définie
D = IR
f

62. Fonctions puissances
Exemples :
f (x) = (2x +1)− 3/ 4
1
On a : f (x) =
2.
; racine paire,
4 (2x +1)3
on doit avoir :
(2x +1)3 ≥ 0
et
(2x +1)3 ≠ 0
(2x +1)3 > 0 ⇔ 2x +1> 0 ⇔ x > −1/ 2
Df =]−1/ 2;+∞[

63. Exemples
5. Fonctions logarithmiques :
f (x) = ln(u(x)) ; ln désigne le logarithme népérien
Df = x∈IR u(x) > 0






Exemple :






f (x) =ln(1−x 2)
2





Df = x∈IR 1− x > 0
or
;
1−x 2 =(1−x)(1+ x) , tableau des signes

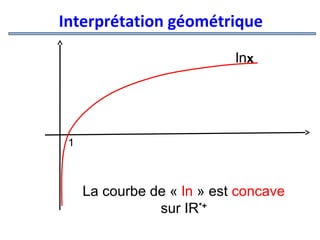
64. Fonctions logarithmiques
Exemple :
x
1-x
f (x) =ln(1−x 2)
∞
1+x
1-x2
Ainsi :
-1
+
-
+
0
0
+
+
1
0
-
0
+
-
Df =]−1;+1[

65. Exemple 2 : f (x) =ln((2x +7)(x −5))
Df = x∈IR (2x + 7)(x −5) > 0







Tableau des signes :
x
2x+7
x-5
Donc :
Produit
-7/2
- 0
+
+
-
0
5
+
0
0
+
+
Df =]− ∞;−7 / 2[∪]5;+∞[

66. Exemples
6. Fonctions exponentielles :
u (x )
f (x ) = e
; alors
Df = Du
« l’exponentielle est toujours définie »
Exemples :
2
f (x) =ex + x +2 ⇒D =IR ;
f
• f (x) =e x ⇒D = IR +
;
f
1/(x −2) ⇒D = IR −2

 
• f (x ) = e
 

f
•

67. A. Fonctions à une variable réel
3.Continuité
I⊂ IR
x I
f
IR
f (x )
f est une fonction définie sur un intervalle I de IR

68. 3. Continuité
a)Continuité en un point a :
a droite de a
a gauche de a
a

69. 3. Continuité
a)Continuité en un point a :
Définition : f est continue au point a lorsque :
lim f (x) = lim f (x) = f (a)
−
+
x →a
x →a
limite à droite = limite à gauche = image de
a

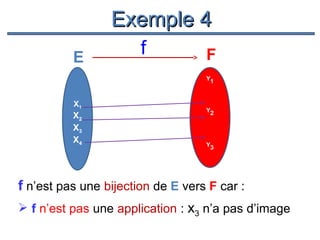
70. Exemples
1.
x ;si x∈[0;1]
f (x ) =
; continuité en 1
2 − x ;si x∈]1;2]







On a :
et
lim f (x) = lim 2 − x = 1 =1
+
+
x →1
x →1
lim f (x) = lim x = 1 =1
−
−
x →1
x →1
f (1) = 1 =1 ; f est donc continue au point 1

71. 2.
x +1;si x∈[0;1[
f (x) = 2 − x;si x∈]1;2]
f (1) = 3/ 2
On a :









; continuité en 1
lim f (x) = lim 2 − x = 2 −1=1
+
+
x →1
x →1
lim f (x) = lim x +1=1+1= 2
−
−
x →1
x →1
et f (1) = 3/ 2 ;
f est donc discontinue au point 1

72. 3. Continuité
b)Continuité sur un intervalle :
Définition :
f est continue sur l’intervalle I=[a;b] lorsque f
est continue en tout point de l’intervalle ouvert
]a;b[ ; continue à gauche de b et continue à
droite de a.

73. • f est continue à gauche de b lorsque :
lim f (x) =f (b)
−
x →b
• f est continue à droite de a lorsque :
lim f (x) =f (a)
+
x →a

74. Continuité sur un intervalle [a ; b]
à gauche de b
à droite de a
a
x
b

75. Exemples
x ;si x∈[0;1]
1. f (x) =
2 − x ;si x∈]1;2]







;
f est continue sur l’intervalle [0 ; 2] car :
• f est continue en tout point de l’intervalle
]0 ; 2[ (en particulier au point 1),
• f est continue a droite de 0 et à gauche de 2.

76. Exemples
2.
x +1;si x∈[0;1[
f (x) = 2 − x;si x∈]1;2] ;
f (1) = 3/ 2









f n’est pas continue sur l’intervalle [0 ; 2] car
elle discontinue au point 1

77. Séance n° 3

78. Propriétés des fonctions continues
Si f et g sont deux fonctions continues sur un
intervalle I alors :
•
•
f +g est continue sur I
αf est continue sur I (α∈IR)
•
f ×g est continue sur I
•
f / g est continue sur I (g ≠ 0 sur I )

79. Conséquences
• Les fonctions polynômiales sont continues
sur IR
• Les fonctions rationnelles ; racines nèmes ;
puissances ; logarithmiques et
exponentielles sont continues sur leurs
domaines de définition

80. bijection et bijection réciproque
I
f
J
f-1
f est une fonction bijective de I vers J. Si f est
continue sur l’ intervalle I alors sa fonction
réciproque f-1 est continue sur l’intervalle J
(car les courbes de f et f-1 sont symétriques par
rapport à la droite d’équation y = x)

81. Remarque
f est continue sur l’ intervalle I
⇔
sa courbe Cf est continue
« ne présente aucune coupure »
Voir TD (Exercice 2)

82. Théorème des Valeurs Intermédiaires
« T.V.I »
T.V.I : Si f est continue sur l’intervalle [a; b]
et
f (a)×f (b) <0 alors f s’annule sur ]a ; b[ ;
C’est-à-dire :
∃c∈ a;b[ tel que : f (c) =0
]

83. Interprétation géométrique
f(b) > 0
a
I
f(a) < 0
c
b
I

84. Ou
f(a) > 0
a
I
c
b
I
f(b) < 0

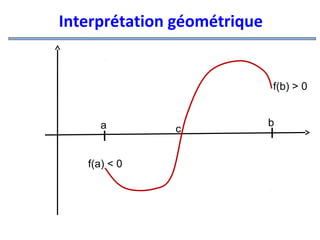
85. Exemple
Montrer que la fonction f (x) = x3 + x −3
s’annule (au moins une fois) sur [0 ; 2]
 La fonction f est une fonction polynomiale
donc définie et continue sur IR, en particulier
sur l’intervalle [0 ; 2]. De plus :
f (0) = −3<0 et f (2) =7 >0
Donc d’après le T.V.I : ∃c∈ 0;2[
]
tel que f (c) =0

86. A. Fonctions à une variable réel
4.Dérivabilité
I⊂ IR
x I
f
IR
f (x )
f est une fonction définie sur un intervalle I
I
a
I
x0
I
b

87. a) Dérivabilité en un point x0
Définition
On dit que la fonction f est dérivable en x0 si :
lim
x→x
f (x ) − f (x )
0
x−x
0 existe.
0
Cette limite « quand elle existe » est appelée :
dérivée de f au point x0 et on la note f’(x0)

88. Ainsi
f '(x0) = lim
x→x
f (x) − f (x )
0
x−x
0
0
A retenir :
toutes les formules de dérivation qu’on
utilise sont une conséquence directe de
cette définition.

89. Exemples
1. Pourquoi la dérivée d’une constante est
égale à 0 ?
On pose :
f (x) =C , soit x0∈IR
I
x0
IR

90. f (x) −f (x )
f '(x0) = lim
x →x
0
x −x
0
0
C −C =0
= lim
x → x x −x
0
Ainsi :
0
∀x0∈IR, f '(x0) =0
Ou encore (en notant x au lieu de x0) :
∀x∈IR,
f '(x) =0

91. Exemples
2. Pourquoi :
(ax2 + bx + c)'= 2ax + b
On pose : f (x) =ax 2 +bx +c , soit
x0∈IR
I
x0
f '(x0) = lim
x →x
0
f (x) −f (x )
x −x
0
0

92. Donc :
= lim
x →x
2
+bx +c) −(ax +bx +c)
0
0
x −x
0
= lim
x →x
(ax
2
a(x
0
2
0
2
−x ) +b(x −x )
0
0
x −x
0
= lim a(x + x0) +b =a(x0 +x0) +b
x →x
0
= 2ax0 +b

93. Ainsi :
∀x ∈IR, f '(x ) =2ax +b
0
0
0
Ou encore (en notant x au lieu de x0) :
∀x∈IR, f '(x) =2ax +b
finalement :
f (x) = ax2 + bx + c ⇒ f '(x) = 2ax + b

94. 3. Pourquoi :
Exemples

'
1
1

 =−


2
x


x
1
On pose : f (x) =
x
f '(x0) = lim
x →x
0
, soit
x0∈IR*
f (x) −f (x )
x −x
0
0

95. Donc :
f '(x0) = lim
x →x
0
1− 1
x x0
x −x 0
x 0 −x
= lim
x →x
−(x −x 0 )
0
xx 0
x −x 0
1
= lim
= lim −
xx 0
x → x xx (x −x ) x →x
0
0
0
0
1 ⇒f '(x ) =− 1
=− 2
0
2
x0
x0

96. finalement :
*, f '(x ) =− 1
∀x ∈IR
2
0
0
x
0
Ou encore (en notant x au lieu de x0) :
*, f '(x) =− 1
∀x∈IR
2
x
Les formules qui suivront sont aussi
conséquence
directe
de
la
définition
précédente :

97. b) Mémento du petit dériveur
fonction
ax+b
xα ( α∈Q )
fonction dérivée
a
αxα −1
x
1 /2 x
lnx
1/x

98. fonction
ex
fonction dérivée
ex
Sin x
Cos x
Cos x
-Sin x
tanx
1+ tan2x

99. Plus général : (u désigne une fonction)
fonction
au+b
uα ( α∈Q )
fonction dérivée
au’
αu'×uα −1
u
u' /2 u
lnu
u'/u

100. fonction
eu
fonction dérivée
u'×eu
Sin u
u'×Cos u
Cos u
-u'×Sin u
tanu
(1+ tan2u)×u'

101. Sans oublier, lorsque la fonction se présente
sous forme de « blocs », qu’on a :
fonction
fonction dérivée
u+ v
u'+v'
u×v
u'v+uv'
u/v
(u'v−uv')/v2
uv
(u'v)×v'

102. Exercice
Calculer les dérivées des fonctions suivantes :
2x
1.f(x) = x 2 −1
2.f(x) = ln(x 2 + x −3)
3.f(x) =
4.f(x) =
x eSinx
5 (x +1)3
(x 2 +1)2/15
5.f(x) =

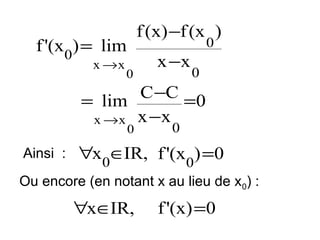
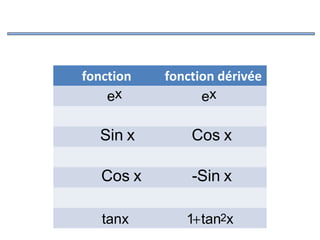
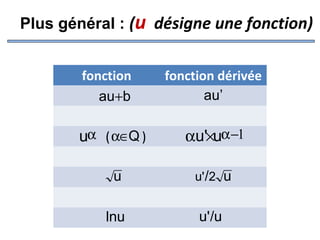
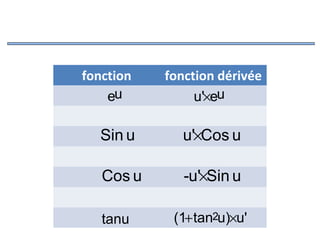
103. c) Dérivabilité sur un intervalle
Définition
Une fonction f est dérivable sur l’intervalle
[a ; b] si elle est dérivable en tout point
de [a ; b]

104. Exemples
1.
f (x ) = x
définie et continue sur
[0;+∞[
1 définie pour x∈ 0;+∞[
]
f '(x) =
2 x
Donc la fonction f n’est pas dérivable sur
[0;+∞[ car f n’est pas dérivable en 0, mais
dérivable seulement sur l’intervalle ]0;+∞[

105. Exemples
2.
3
f (x ) =
x −1
définie et continue IR
Question :
f est-elle dérivable sur l’intervalle [0 ; 2] ?
3
f (x ) =
1/ 3 ⇒ f '(x) = 1 (x −1)− 2 / 3
x −1 = (x −1)
3
C’est-à-dire :
f '(x) =
1
3
3
(x −1)
2

106. f '(x) =
1
2
3 (x −1)
3
donc f n’est pas dérivable en x = 1, et par
conséquent f n’est pas dérivable sur l’intervalle
[0 ; 2]

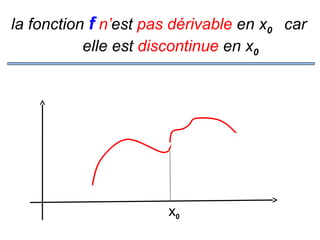
107. Remarques
1. f est dérivable en x0
⇒ f est continue en x
2. f est dérivable sur [a ; b]
sur [a ; b]
⇒ f est continue
0

108. Donc « contraposée »
3. f est discontinue en x0
dérivable en x0
⇒ f n’est pas
4. f est discontinue sur [a ; b]
dérivable sur [a ; b]
Contraposée :
p⇒ q
⇒f n’est pas
⇔ non q ⇒ non p

109. la fonction f n’est pas dérivable en x0 car
elle est discontinue en x0
x0

110. Séance n° 4

111. Exercice « Corrigé »
Calculer les dérivées des fonctions suivantes :
2
1.f(x) =
2x ⇒f '(x) =− 2(x +1)
2
2
x 2 −1
(x −1)
2.f(x) =
ln(x 2 +x −3) ⇒f 'x) =
2x +1
2
x +x −3
x eSinx
3.f(x) =
1 eSinx + x CosxeSinx
⇒f '(x) =
2 x

112. Exercice « Corrigé »
4.f(x) =
5.f(x) =
(x +1)3 =(x +1)3 / 5
3
⇒f '(x) =
5 (x +1) 2
5
5
(x 2 +1)2/15
4x
⇒f '(x) =
15 (x 2 +1)13
15

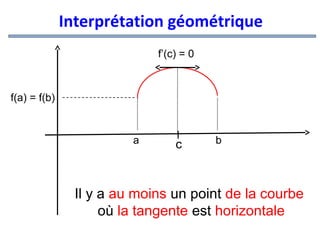
113. Théorème de Rolle
Théorème :
Si f est une fonction continue sur l’intervalle
[a ; b] ; dérivable sur l’intervalle ouvert ]a ;
b[ etf:(a) =f (b)
alors :
∃c∈ a;b[ tel que f '(c) =0
]

114. Interprétation géométrique
f’(c) = 0
f(a) = f(b)
a
I
c
b
Il y a au moins un point de la courbe
où la tangente est horizontale

115. Remarque
Les hypothèses du Théorème de Rolle :
a) f est continue sur [a ; b]
b) f est dérivable sur ]a ; b[
c) f(a) = f(b)
sont nécessaires.

116. Exemple
Peut-on appliquer le Théorème de Rolle
à la fonction :
2
3
f (x) =1− (x −1)
sur l’intervalle [0 ; 2] ?

117. Réponse
a)
3
f (x) =1−
(x −1)
2
: la racine cubique
« racine impaire » est définie sur IR, donc
Df = IR
• f est la somme d’une fonction constante
3 (x −1) 2
«1» et d’une fonction racine « −
»
donc continue sur son domaine de définition
IR,
en particulier f est continue sur l’intervalle [0 ; 2]

118. Réponse
b)
2 =1−3 1 =0
f (0) =1− (0 −1)
3
2 =1−3 1 =0
f (2) =1− (2 −1)
3
ainsi
f(0) = f(2)

119. Réponse
c) Dérivabilité de f sur l’intervalle ]0 ; 2[
f (x) =1−3
2
(x −1) =1−(x −1)2 / 3
2
⇒f '(x) =−
33 x −1
 f n’est pas dérivable en x = 1 « f’(1) n’est
pas définie », donc f n’est pas dérivable

120. Conclusion
On ne peut pas appliquer le Théorème de
3
Rolle à la fonction f (x) =1−
(x −1)
2
sur l’intervalle [0 ; 2] car l’hypothèse de
dérivabilité n’est pas vérifiée !!!
Voir Exercice 5, Série de TD

121. Théorème des accroissements finis
« T.A.F »
Théorème :
Si f est une fonction :
a) continue sur [a ; b]
b) dérivable sur ]a ; b[
alors : ∃c∈ a;b[ tel que :
]
f (b) −f (a) =(b −a)f '(c)

122. 2
ème
version « T.A.F »
Théorème :
Si f est une fonction :
a) continue sur [a ; b]
b) dérivable sur ]a ; b[
alors : ∃c∈ a;b[ tel que :
]
f (b) −f (a) =f '(c)
b −a

123. 3ème version « T.A.F »
… premier développement limité
Théorème :
Si f est une fonction :
a) continue sur [a ; b]
b) dérivable sur ]a ; b[
alors : ∃c∈ a;b[ tel que :
]
f (b) =f (a) +(b −a)f '(c)

124. Remarque : Pourquoi on dit :
accroissements finis ?
Comme
f (b) −f (a) =(b −a)f '(c)
« 1ère version »
Si la dérivée première « f’ » est une fonction
bornée :
f '(x) ≤ M sur l’intervalle considéré,
alors on a :
f (b) −f (a) ≤M(b −a)

125. Ainsi, si l’ordre de grandeur de f’ est fixé,
les accroissements de la fonction f « f(b)f(a) » sont bornés « finis »

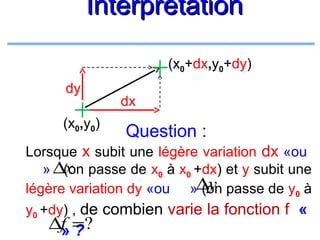
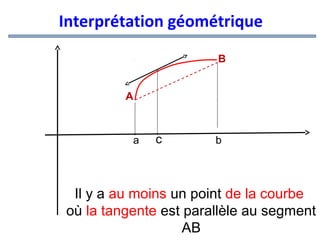
126. Interprétation géométrique
∃c∈ a;b[
]
f (b) −f (a) =f '(c)
tel que
b −a
Veut dire : Il y a au moins un point de la courbe
où la tangente est parallèle au segment AB

127. Interprétation géométrique
B
A
a
c
b
Il y a au moins un point de la courbe
où la tangente est parallèle au segment
AB

128. Conséquences
f est une fonction continue et dérivable sur
l’intervalle [a ; b] :
•
Si f’(x)=0 (x∈[a;b] ) alors f est constante
∀
•
≥ (
Si f’(x) 0∀x∈[a;b] ) alors f est
croissante
•
≤
∀x∈[a;b]
Si f’(x) 0 (
décroissante
) alors f est

129. Preuve
a
I
x
I
c
I
y
I
b
I
Soient x et y deux nombres quelconques
de l’intervalle [a ; b] tels que : x≤ y
• Si f’(x)=0 (∀x∈[a;b] ), dans ce cas ; T.A.F :
f (y) −f (x) =(y −x)f '(c) =(y −x)×0 =0
⇒f (y) =f (x) : f est donc constante sur
l’intervalle [a ; b]

130. Preuve
• Si f’(x) ≥0 (∀x∈[a;b] ), dans ce cas ; T.A.F :
f (y) −f (x) =(y −x)f '(c) ≥0
y −xcar0:
≥
f '(c) ≥et ⇒f (y) ≥f (x)
0
f est donc croissante sur l’intervalle [a ; b]

131. Preuve
• Si f’(x) ≤0 (∀x∈[a;b] ), dans ce cas ; T.A.F :
f (y) −f (x) =(y −x)f '(c) ≤0
y −xcar0:
≥
f '(c) ≤et ⇒f (y) ≤f (x)
0
f est donc décroissante sur l’intervalle [a ; b]

132. A. Fonctions à une variable réel
5.Calcul de limites
« Règle de l’HOSPITAL »
Exemple :
lim Sinx =?
x→0 x
Problème : lorsque x →0 :
Sinx →0 et x →0

133. 0 =?
La forme indéterminée
0
Exemples :
1.
2.
3.
x 2 = lim x =;0
lim x
x→0
x→0
x = lim 1 =±∞
lim 2
;
x→0 x
x→0 x
.
lim 5x =5
x→0 x

134. La forme indéterminée
Nous avons une forme indéterminée
lorsqu’on ne peut pas prévoir le résultat
d’avance.
Les formes indéterminées :
0 =? ; ∞=? ; ∞−∞=? ;
0×∞=?
0
∞

135. 0 =?
La forme indéterminée
0
0 =? , on peut
Pour la forme indéterminée
0
utiliser la Règle de l’Hospital :
R-H :
Si
lim f (x) = lim g(x) =0
x→a
x→a
f (x) = lim f '(x)
lim
alors x→
a g(x) x→a g'(x)

136. Exemples
1.
lim Sinx =?
x
x→0
Règle de l’Hospital :
lim Sinx = lim Cosx =Cos0 =1
x→0 x
x→0 1

137. Exemples
2.
lim ln x =?
x→ x −1
1
Règle de l’Hospital :
lim ln x = lim 1/ x =1/1=1
x→ x −1 x→ 1
1
1

138. Exemples
ex −1=?
3. lim
x→0+ x2
Règle de l’Hospital :
ex −1=
lim+
x→0 x2
0
ex = e = 1 =+∞
lim+
x→0 2x 0+ 0+

139. Remarque
La règle de l’Hospital est un outil
puissant pour le calcul des limites.
Elle peut être utilisée plusieurs fois
de suite.

140. Exemples
4.
ex −x −1=?
lim
x→0 x2
Règle de l’Hospital « 1ère fois »:
ex −1
= lim
x→0 2x
Règle de l’Hospital « 2ème fois »:
0
ex = e = 1
= lim
x→0 2 2 2

141. Exemples
sin x −x −x3 =?
5. lim
x4
x→0+
Règle de l’Hospital « 1ère fois »:
Cosx −1−3x 2
= lim+
x→0
4x3
Règle de l’Hospital « 2ème fois »:
= lim+ −Sinx −6x
x→0
12x 2

142. Exemples
Règle de l’Hospital « 3ème fois »:
−Cosx −6 = −7 =−∞
= lim+
+
x→0
24x
0

143. Séance n° 5

144. A. Fonctions à une variable réel
6.Dérivées d’ordre supérieur;
Formule de Taylor
Développements limités

145. Dérivées d’ordre supérieur
La dérivée d’ordre n (on dit aussi : la
dérivée nème) s’obtient en dérivant f n
fois :
f
on
dérive
f’
on
dérive
on
dérive
f’’
on
dérive
on
dérive
f(3)
f(n)

146. Exemples
1. f (x) =ln x
•
f '(x) =1/ x
;
f ''(x) =−1/ x 2
•
•
f (3)(x) =2 / x3
;
; …;
(n)(x) =(−1)n +1(n −1)!/ x n
• f

147. Exemples
2.
f (x) =ex
•
f '(x) =ex
•
f ''(x) =ex
•
f (n)(x) =ex
;
;…;

148. Utilisation de la dérivée
seconde « f’’ »
Convexité & Concavité
f
on
dérive
f’
on
dérive
f’’

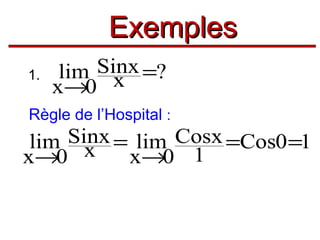
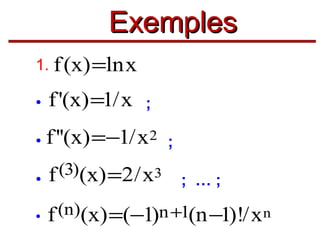
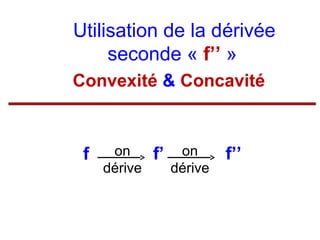
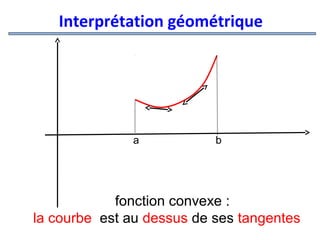
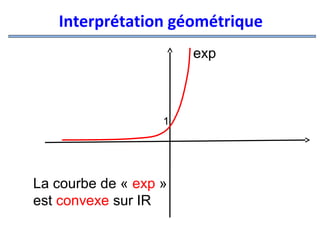
149. Convexité
Définition
Une fonction
f est dite convexe sur
l’intervalle [a ; b] lorsque sa courbe C f sur
l’intervalle [a ; b] est au dessus de toutes
ses tangentes

150. Interprétation géométrique
a
b
fonction convexe :
la courbe est au dessus de ses tangentes

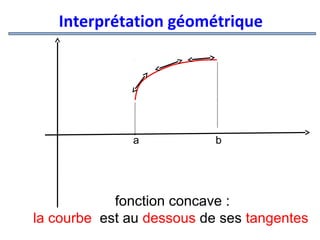
151. Concavité
Définition
Une fonction
f est dite concave sur
l’intervalle [a ; b] lorsque sa courbe C f sur
l’intervalle [a ; b] est au dessous de toutes
ses tangentes

152. Interprétation géométrique
a
b
fonction concave :
la courbe est au dessous de ses tangentes

153. Convexité
Si
f ''(x) ≥0
Théorème
ceci
∀x∈ a;b] , alors
[
la fonction f est convexe sur l’intervalle [a ;
b]

154. Concavité
Si
f ''(x) ≤0
Théorème
ceci
∀x∈ a;b] , alors
[
la fonction f est concave sur l’intervalle [a ;
b]

155. Exemples
Étudier la convexité des fonction
suivantes sur leurs domaines de
définition :
1.
f (x) =ln x ;
2.
f (x) =ex

156. 1. f (x) =ln x ;
f (x) =ln x ⇒f '(x) =1/ x
⇒f ''(x) =−1/ x2 avec x∈D =IR*+
f
ainsi
∀x∈D
f
on a
f ''(x) <0
La fonction « ln » est concave sur
IR*+

157. Interprétation géométrique
lnx
1
La courbe de « ln » est concave
sur IR*+

158. 2.
f (x) =ex ;
f ''(x) =ex >0 ceci ∀x∈Df =IR
La fonction « exp » est convexe sur IR

159. Interprétation géométrique
exp
1
La courbe de « exp »
est convexe sur IR

160. Exercice
Étudier la convexité des fonctions suivantes
sur leurs domaines de définition :
1.
f (x) = x
2.
f (x) =1/ x ;
3.
f (x) =3 x ;
4.
f (x) =x3 −3x2 +x −5
;

161. Dérivées d’ordre supérieur
Formule de Taylor
f(b)
f(a)
a
b
Question fondamentale en Analyse :
Connaissant la valeur de f au point a, peut-on
donner une estimation de f(b) ???

162. Exemple « Météo »
24°
21°
Mardi
Dimanche
Connaissant la température enregistrée Mardi,
peut-on prévoir la température de Dimanche
prochain ???

163. Réponse « Taylor »
f(b)
f(a)
a
b
On peut donner une valeur approchée de f(b),
à condition de connaître f(a)…mais aussi :
f’(a) ; f’’(a) ; f(3)(a) ; f(4)(a) ; …. ; f(n)(a) ; …

164. A savoir :
Notre estimation de f(b) est meilleure lorsque :
 n est grand
 b est proche de a
proches
I
a
I
b

165. Exemple « Météo »
?
22°
21°
Mardi Mercredi
Dimanche
Connaissant la température de Mardi, il est
plus simple de prévoir la température de
Mercredi « proche de Mardi » que celle de
Dimanche « loin de Mardi »

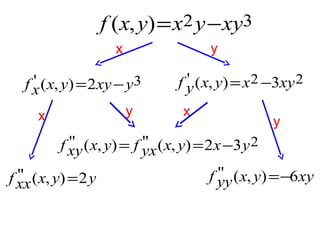
166. La « fameuse » Formule de Taylor
Théorème :
Si f est une fonction dérivable
à l’ordre n+1 alors :
2
(b −a) f ''(a) +
f (b) =f (a) +(b −a)f '(a) +
2!
3
n
(b −a) f (3)(a) +...+ (b −a) f (n)(a) +
3!
n!
n +1
(b −a)
]
f (n +1)(c) avec c∈ a;b[
(n +1)!
I
I
I
a
c
b

167. Développements limités : a=0 et b=x
Théorème :
Si f est une fonction dérivable
à l’ordre n+1 alors :
2
3
x f ''(0) + x f (3)(0) +
f (x) =f (0) + xf '(0) +
...+
avec
n
x
n!
c∈ 0; x[
]
2!
f (n)(0) +
3!
n +1
x
f (n +1)(c)
(n +1)!
c
I
x
I

168. Notation de Young
Formule de Taylor-Young
2
3
x f ''(0) + x f (3)(0) +
f (x) =f (0) + xf '(0) +
2!
3!
n
x f (n)(0) +x nε(x)
...+
n!
x f (n +1)(c)
avec ε(x) =
(n +1)!

169. Remarque
1.
2.
ε(x) →0 lorsque x →0
ε(x) n’est pas une fonction, c’est une
manière symbolique d’écrire : quantité qui
tend vers 0 avec x. Donc :
ε
 La différence de deux (x) n’est pas 0
mais un (x) , prendre par exemple x 2
et x3
 Le produit de deux (x) est un (x)
ε
ε
ε

170. Quelques
Développements limités importants
1. f (x) =ex
; La formule de Taylor-Young
donne :
2
n
x =e0 + xe0 + x e0 +...+ x e0 +x nε(x)
e
2!
n!
Ainsi :
2
n
x =1+ x + x +...+ x +x nε(x)
(D1) e
2!
n!

171. c’est-à-dire : pour x proche de 0
2
n
x ≈1+ x + x +...+ x
e
2!
n!
Exemple :
0,1 ≈1+0,1+ 0,01+...
e
2
−0,1 ≈1−0,1+ 0,01−...
e
2

172. 1 =(1−x)−1
2. f (x) =
:
1−x
La formule de Taylor-Young donne :
•
f (0) =1 ;
•
f '(x) = −1×(1−x)−2 ×(−1) ⇒f '(0) =1 ;
•
f ''(x) = −2×(1−x)−3×(−1) ⇒f ''(0) =2! ;
•
f (3) ( x) = −6×(1− x)− 4 ×(−1) ⇒ f (3) (0) =3!
;
...f (n)(0) =n!
•
on obtient ainsi :

173. 1 =1+x + x 2 +x3 +...+ x n + x nε(x)
(D2)
1−x
En remplaçant x par –x on obtient : (D3)
1 =1−x + x 2 −x3 +...+(−1)n x n + x nε(x)
1+ x
En intégrant D3 on obtient : (D4)
ln(1+ x) = x −
x
2
2
+
x
3
3
+...+
(−1)
n
(n +1)!
x n +1 + x n +1ε(x)

174. Application : calcul de limites
Exemple :
1
Calculer lim (1+x) x
x →0
1
1 (x + xε(x))
ln(1+x)
 (1+x) x =e x
=e x
1
Développement limité (D4) à l’ordre 1

175. Calcul de limites
Ainsi :
1
lim
(1+x) x = lim e
x →0
x →0
car
ε(x) →0
(1+ε(x))
1 =e
=e

176. Séance n° 6

177. Calcul de limites
« Exercice »
Calculer :
1) x )
1. lim x(e −(1+
;
x
x →+∞
5) x
lim (1+
2.
;
x
x →+∞

178. 1 ) 3x
lim (1+
3.
;
x
x →+∞
(x cos x −sin x)
4. lim
; 2
x →0 e x −1−x − x
2

179. corrigé
1 ) x ) =?
1. lim x(e −(1+
x
x →+∞
1)
x x ln(1+
On a : (1+ 1 ) =e
x
x
Or lorsque
x →+∞
alors
1 →0
x

180. 1 ) = 1 − 1 + 1 ε( 1 )
Or ln(1+
2
2
x x 2x x x
Développement limité (D4) à l’ordre 2 !!
Remarque :

1
C’est
qui joue le rôle de x ici, car
x
1 →0 donc 1 est proche de 0
x
x

181. Ainsi :
1 − 1 + 1 ε( 1 ))
x(
1 )x =e x 2x 2 x 2 x
(1+
x
1 + 1 ε( 1 )
1−
2x x x
=e
1 + 1 ε( 1 )
−
1
2x x x
=e ×e

182. Or pour t proche de 0 ( t→0) on a :
t
e =1+t +tε(t)
Développement limité (D1) à l’ordre 1 !!
Donc : ( t =−1/ 2x )
e
1 + 1 ε( 1 )
−
2x x x
1 + 1 ε( 1 )
=1−
2x x x

183. Par conséquent :
1 ) x =e1 ×(1− 1 + 1 ε( 1 ))
(1+
x
2x x x
e + 1 ε( 1 )
=e −
2x x x
finalement :
1 )x ) = x( e + 1 ε( 1 ))
x(e −(1+
2x x x
x

184. C’est-à-dire :
1 )x ) = e +ε( 1 ))
x(e −(1+
2
x
x
Conclusion
1 )x ) = e
lim x(e −(1+
2
x
x →+∞
Car
1 ) = lim ε(t) =0
lim ε(
x →+∞ x t →0

185. 5) x
2. lim (1+
:
x
x →+∞
5)
x ln(1+
x
5 ) x =e
On a : (1+
x
5) = 5 + 1 ε( 1 )
1
Or : ln( +
x x x x
Développement limité (D4) à l’ordre 1

186. 5 →0 lorsque x →+∞
Car
x
Donc :
5) x =e
(1+
x
5 + 1 ε( 1 ))
x(
x x x

187. 1)
5+ε(
x
5) x =e
C’est-à-dire : (1+
x
5 ) x =e 5
lim (1+
Ainsi :
x
x →+∞
Car
1 ) = lim ε(t) =0
lim ε(
x →+∞ x t →0

188. 1 ) 3x
3. lim (1+
:
x
x →+∞
1 ) 3x =e
(1+
x
1 ) = 1 + 1 ε( 1 )
ln(1+
x x x x
On a :
Or :
1)
3x ln(1+
x
Développement limité (D4) à l’ordre 1

189. 1 →0 lorsque x →+∞
Car
x
Donc :
1 ) 3x =e
(1+
x
1 + 1 ε( 1 ))
3x(
x x x

190. 1)
3+ε(
x
1 ) 3x =e
C’est-à-dire : (1+
x
1 ) 3x =e 3
lim (1+
Ainsi :
x
x →+∞
1 ) = lim ε(t) =0
lim ε(
Car
x →+∞ x t →0

191. Remarque
Refaire le calcul des 3 limites
précédente en posant « au début » :
1
t=
x

192. (x cos x −sin x) :
4. lim
2
x →0 e x −1−x − x
2
Nous avons besoin des développements
limités de Cos x et Sin x à l’ordre 3, car
le dénominateur montre qu’il faut
ex
développer la fonction
à l’ordre 3

193.
Développements limités à l’ordre 3
de Cos x et Sin x
1. f (x) =Cosx
;
à
l’ordre 3 donne :
La formule de Taylor-Young
2
x Cos''0
Cosx =Cos0 + xCos'0 +
2!
3
x Cos (3) 0 + x3ε(x)
+
3!

194. Or :
Cos0 =1 ;
Cos'0 =−Sin0 =0
Cos''0 =−Cos0 =−1
Cos(3)0 =Sin0 =0
2
x +0x3 +x3ε(x)
Donc : Cosx =1+0x −
2
C’est-à-dire :
2
x + x3ε(x)
Cosx =1−
2

195. De même pour la fonction Sinus
1.
f (x) =Sinx; La formule de Taylor-Young
à
l’ordre 3 donne :
2
x Sin''0
Sinx =Sin0 + xSin'0 +
2!
3
x Sin (3) 0 +x3ε(x)
+
3!

196. Or :
Donc :
Sin0 =0 ;
Sin'0 =Cos0 =1
Sin''0 = −Sin0 =0
Sin(3) 0 = −Cos0 = −1
2
3
x
x ×0 + ×−1+ x3ε(x)
Sinx =0 + x ×1+
2
6
C’est-à-dire :
3
x + x3ε(x)
Sinx = x −
6

197. x cos x −sin x =
Par conséquent :
2
x
x
e −1−x −
2
2 / 2) −(x −x 3 / 6) +x 3ε(x)
x(1−x
3 / 6+x 3ε(x)
x
Nous avons utiliser le D. L. de ex à l’ordre 3

198. 3 / 3+x 3ε(x) −1/ 3+ε(x)
−x
=
=
3 / 6+x 3ε(x) 1/ 6+ε(x)
x
Ainsi :
(x cos x −sin x) =−2
lim
2
x →0 e x −1−x − x
2

199. 2
ème
Partie du Cours
B. Fonctions à deux
variables réelles

200. Exemples introductifs
I. Une entreprise commercialise 3 produits :
A, B et C. Le prix de vente unitaire du
produit A est 12 DH, celui du produit B est
15 DH et celui du produit C est 22 DH.
 On vend une quantité x du produit A, une
quantité y du produit B et une quantité z
du produit C. La recette R(x ; y ; z) est
donnée par :
R(x ; y ; z) = 12x + 15y + 22 z
La recette de cet exemple est une fonction
de 3 variables x, y et z

201. Exemples introductifs
II. Une entreprise fabrique 2 produits A et B.
Si x désigne la quantité fabriquée de A et
y celle de B, la recette escomptée lors de
la vente de x articles de A et de y articles
de B est donnée par :
R(x , y) = -3x2 -2y2 +220x +140y
 Le coût d’une unité de A (respectivement
de B) qu’on note CA (respectivement CB)
dépend des quantités x et y comme suit :
CA = 2x +y et CB = x +3y

202. Exemples introductifs
a. Exprimer en fonction de x et de y le coût
c(x , y) de fabrication de x unités de A et
de y unités de B.
 C(x , y) = x CA + y CB
= x (2x +y) + y (x +3y)
= 2x2 +3y2 +2xy
On obtient une fonction de 2 variables x et y

203. Exemples introductifs
b. Exprimer le bénéfice B(x , y) réalisé lors de
la vente de x articles de A et de y articles de
B.
 B(x , y) = R(x , y) – c(x , y)
= (-3x2 -2y2 +220x +140y) – (2x2 +3y2 +2xy)
= -5x2 -5y2 -2xy +220x +140y
le bénéfice est une fonction de 2 variables x et
y

204. Séance n° 7

205. Exemples de fonctions à
plusieurs variables
a.
y +yex
f (x, y) =xe
x + y +100
b. f (x, y) =
y x
c.
: 2 variables
: 2 variables
f (x, y) =x3 +y3 −3xy
: 2 variables

206. Exemples de fonctions à
plusieurs variables
d.
f (x, y, z) = xyz −x +5 y +3z : 3 var
e.
f (x, y, z) =ln(x2 + y2 −4z)
f.
f (x, y, z,t) = x3 + y2 −z + t
:3 var
:4 var

207. Remarque
1. Dans le cas de n variables (
peut noter les variables :
n≥5 ), on
x1 , x2 , x3 , … , xn
la fonction f est notée dans ce cas :
f(x1 , x2 , x3 , … , xn)

208. Remarque
2. On s’intéresse dans le cadre de ce cours
aux fonctions de deux variables x et y
(x, y)∈IR×IR →f (x, y)

209. 1.Domaine de définition
D f ⊂ IR× IR
( x, y) I
f
IR
f ( x, y)
Le domaine de définition est
un domaine du plan IR2
(IR2 = IR x IR)

210. Interprétation géométrique
y
Le plan IR2
x

211. Interprétation géométrique
Df
Df ⊂ IR
2

212. Exemples
1.

f (x, y) =x2 +y2 −xy −2x +y
∀x∈IR
et
∀y∈IR
:
on a :
f (x, y) est définie (on peut la calculer)
Donc
D =IR×IR =IR
f
x
y
2

213. Interprétation géométrique
D =IR×IR
f
le plan tout
entier

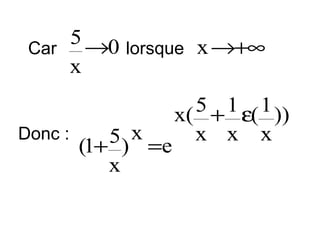
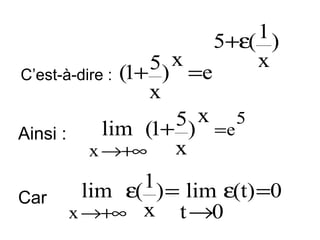
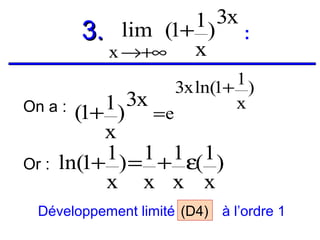
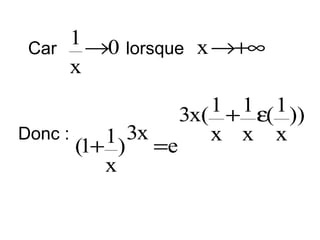
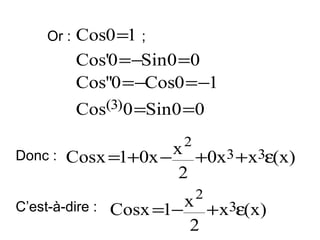
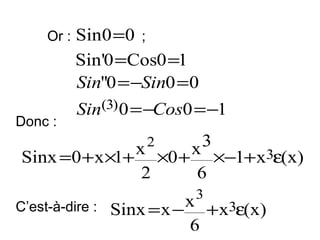
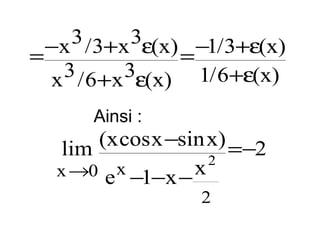
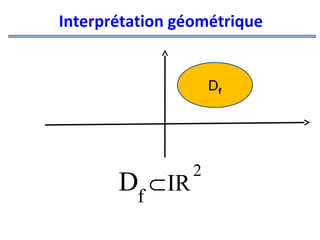
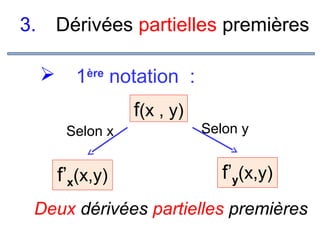
214. Exemples
2.
f (x, y) =x ln(y) +y2 +3
 on doit avoir
y>0
pour que f (x, y)
soit définie, donc
D =IR×]0,+∞[
f
x
:
y

215. Interprétation géométrique
y
D
f
x
la moitié
supérieure
du plan
Sans l’axe Ox

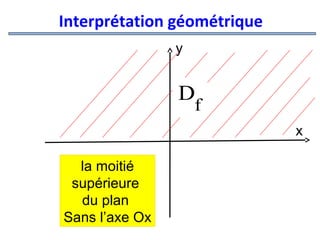
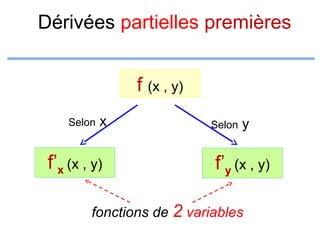
216. Exemples
3.
f (x, y) =ln(x) +ln(y) +1 :
 On doit avoir :
pour que
Donc
x >0
et
y>0
f (x, y) soit définie
D =]0,+∞[×]0,+∞[
f
x
y

217. Interprétation géométrique
D
f
¼ du plan
Sans les
axes

218. Remarque
à réviser :
 Équation d’une droite dans le plan IR 2 :
Une droite partage le plan en 3 zones…..
 Équation d’un cercle dans le plan IR 2 :
Un cercle partage le plan en 3 zones…..
Voir TD

219. Exercice
Voir Exercice 1
« TD, Partie 2 »

220. 2.Courbes de niveaux & Sections
a) Courbes de niveaux :

Ce sont des sous ensembles du
domaines de définition D.
 Elles correspondent à des coupes
horizontales de la surface z = f(x , y)
projetées sur le domaine de définition
D.

221. a)Courbes de niveaux
Définition
 La courbe de niveau k, notée Ck ou Nk,
est l’ensemble des points du domaine de
définition D tels que leur image f(x , y) est
égale à k :
C = (x, y)∈D /f (x, y) = k
k











222. Exemple
•

f (x, y) = y −x2
D =IR
:
2
f
 La Courbe de niveau k : On cherche les
couples (x , y) du domaine de définition IR 2
tels que :
f (x, y) = k

223. f (x, y) = k ⇔ y − x2 = k ⇔ y = x2 + k
La Courbe de niveau k est la parabole
d’équation y = x 2 +k :
 C0 : (k=0) parabole d’équation
 C1 :(k=1)
//
//
 C-1 :(k=-1) //
//
y=x2
y =x2 +1
y =x2 −1

224. b) Sections ou « abaques »

Elles correspondent à des coupes
verticales de la surface z = f(x , y)

225.  Sections selon x
 On fixe x : ( x = k ) et on trace la
courbe z = f(k , y) dans le plan Oyz
z
y

226.  Sections selon y
 On fixe y : ( y = k ) et on trace la
courbe z = f(x , k) dans le plan Oxz
z
x

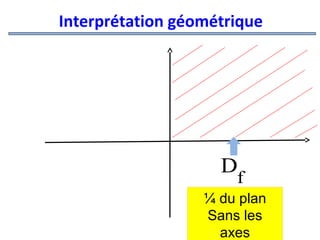
227. Exemple
•
f (x, y) =ln(xy)
:
 Domaine de définition :
xy > 0 ⇔ x > 0
et
y> 0 ou x < 0 et y< 0
D =]−∞,0[×]−∞,0[∪]0,+∞[×]0,+∞[
f

228. Interprétation géométrique
D
f

229. Section selon x = 1
 On fixe x : ( x = 1 ) et on trace la
courbe : z = f(1 , y) = ln y (y>0)
dans le plan Oyz
z
z=ln y
y

230. Section selon y = -1
 On fixe y : ( y = -1 ) et on trace la
courbe : z = f(x , -1) = ln -x (x<0)
dans le plan Oxz
z=ln -x
z
x

231. 3.
Dérivées partielles premières

1ère notation :
f(x , y)
Selon x
f’x(x,y)
Selon y
f’y(x,y)
Deux dérivées partielles premières

232. 2
ème
notation
∂ : Se prononce « d rond »
f(x , y)
Selon x
∂f (x, y)
∂x
∂f (x, y)
∂y

233. Règle de base
Les premiers pas…dans le calcul différentiel
Lorsqu’on dérive par rapport à
une variable, l’autre variable
est supposée constante

234. Dérivées partielle première
par rapport à x
'
f x ( x0, y0) = lim
x→ x
0
f ( x, y ) − f ( x , y )
0
x− x
0
0
x est variable et tend vers x0,
alors que y est fixé : y = y0
0

235. Dérivées partielle première
par rapport à y
'
f y ( x0, y0) = lim
y→ y
f ( x , y) − f ( x , y )
0
0
y− y
0
0
x est fixé : x = x0 alors que y est
variable et tend vers y0
0

236. Remarque
Lorsqu’on calcule une dérivée
partielle, on utilise les règles de
dérivation d’une fonction d’une
variable réelle
« car une des deux variable est fixée »

237. Exemples
1. f (x, y) =x2 +xy + y4 +3 :
Selon x
'
f x (x, y) =2x +y
Selon y
'
f y(x, y) =x +4y3

238. Exemples
y +x 2y :
2. f (x, y) =xe
Selon x
Selon y
'
' (x, y) =ey +2xy f y(x, y) =xey +x2
fx

239. Exemples
3. f (x, y) =x3 + y3 −3xy :
Selon x
Selon y
'
'
f x (x, y) =3x2 −3y f y(x, y) =3y2 −3x

240. Séance n° 8

241. Dérivées partielles premières
f (x , y)
Selon
x
f’x (x , y)
Selon
y
f’y (x , y)
fonctions de 2 variables

242. Une dérivée partielle est une
fonction de deux variables x et y,
on peut alors la dériver à son tour!

243. Schème de dérivation
f(x , y)
x
y
f’x(x,y)
x
f’’xx(x,y)
y
f’’xy(x,y)
f’y(x,y)
x
f’’yx(x,y)
y
f’’yy(x,y)
quatre dérivées partielles secondes

244. Dérivées partielles secondes
ou d’ordre 2
f’’xx
: On dérive f 2 fois par rapport à x
f’’xy
: On dérive f par rapport à x ensuite
f’’yx
f’’yy
par rapport à y « dérivée croisée »
: On dérive f par rapport à y ensuite
par rapport à x « dérivée croisée »
: On dérive f 2 fois par rapport à y

245. Exercice
 Calculer les dérivées partielles
premières
et
secondes
des
fonctions suivantes :
1. f (x, y) =3x 2y −xy3 −x −y ;
2. f (x, y) = x ln y + yln x ;
2
2 ;
3. f (x, y) = x + y

246. f (x, y) =3x2y −xy3 −x −y :
1.
y
x
'
f x ( x, y) = 6 xy − y3 −1
y
x
'
f y ( x, y) =3x2 −3xy2 −1
x
y
''
''
f xy ( x, y) = f yx ( x, y) = 6 x −3 y 2
''
f xx ( x, y) = 6 y
Remarque :
''
f yy ( x, y) = −6xy
''
''
f xy = f yx

247. 2. f (x, y) =x ln y + yln x
y
x
'
f x ( x, y) = ln y + y / x
y
x
:
'
f y ( x, y) = x / y +ln x
x
y
''
''
f xy ( x, y) = f yx ( x, y) =1/ x +1/ y
''
f xx ( x, y) = − y / x2
Remarque :
''
f yy ( x, y) = −x / y 2
''
''
f xy = f yx

248. 3. f ( x, y) = x 2 + y 2
:
y
x
' ( x, y) = x / x 2 + y 2 f ' ( x, y) = y / x 2 + y 2
fx
y
y
x
x
y
'' = f '' = −xy / ( x 2 + y 2 )3
f xy
yx
''
f xx = y 2 / ( x 2 + y 2 )3
''
f yy = x2 / ( x 2 + y 2 )3

249. Remarque
a)
Théorème de Schwartz
Si f est une fonction «de classe C2»
alors les dérivées secondes croisées
sont égales : f '' = f ''
xy

yx
Toutes les fonctions économiques
considérées dans ce cours vérifient
le Théorème de Schwartz

250. Remarque
b)
Une fonction de deux variables
admet :
1.
2.
3.
4.
n.
2 dérivées partielles d’ordre 1 « premières »
4 dérivées partielles d’ordre 2
8 dérivées partielles d’ordre 3
16 dérivées partielles d’ordre 4 … etc
2n dérivées partielles d’ordre n

251. 4. Quelques définitions
a)
Les fonctions homogènes :
Définition
f est homogène de degré k lorsque :
∀(x, y)∈D
f
et
∀α >0
f (αx,αy) =αk f (x, y)

252. Exemples
1.
f (x, y) =5x2 y −xy2
Soit
:
α > 0 , on a :
f (αx,αy) =5(αx)2(αy) −(αx)(αy)2
⇒ f (αx,αy) =5α3x2 y −α3xy2
=α3(5x2 y − xy2) =α3 f ( x, y)
f est homogène de degré 3

253. 2. f ( x, y) = 2
xy
x −y
Soit
2 :
α > 0 , on a :
f (αx,αy) =
(αx)(αy)
2 2
2 2
α x −α y
=
xy
2
x −y
2
⇒ f (αx,αy) = f ( x, y) =α0 f (x, y)
f est homogène de degré 0

254. 3. f ( x, y) = 5
y
x +y
Soit
5 :
α > 0 , on a :
f (αx,αy) =
αy
5 5
5 5
α x +α y
=α −4
y
5
x +y
⇒ f (αx,αy) =α −4 f (x, y)
f est homogène de degré -4
5

255. 4.
Soit
f (x, y) = xy + x + y +1:
α > 0 , on a :
f (αx,αy) =α 2 xy +αx +αy +1
Si on prend par exemple α = 2 et
x =1, y =1
f (2×1,2×1) = f (2,2) =9
f (1,1) =4⇒ f (2×1,2×1) ≠2× f (1,1)
On obtient :
f n’est pas une fonction homogène

256. Règle Pratique
Pour montrer que f est homogène (ou non
homogène), on peut utiliser :
 La définition
ou
 Le Théorème d’Euler

257. Théorème d’Euler
f est homogène de degré k
⇔
'
'
xf x(x, y) + yf y (x, y) = k × f (x, y)

258. Exemple
f (x, y) =5x2 y −xy2
x
'
f x ( x, y) =10 xy − y 2
y
'
f y ( x, y) =5x2 −2xy
'
'
On a : xf x ( x, y) + yf y ( x, y) =15x2 y − 3xy2
'
'
⇒ xf x( x, y) + yf y ( x, y) = 3 f ( x, y)
f est homogène de degré 3

259. 4. Quelques définitions
b)
Elasticités
1. Cas d’une fonction d’une variable :
L’élasticité de f est par définition :
x
xf '(x)
E =e( f , x) =
f
f (x)

260. Exemple
f (x) = x2 + x −2
On a :
x(2x +1)
2
2x + x
e( f , x) =
=
=
2
2
f ( x) x + x −2 x + x −2
xf '( x)
5
Exemple : e( f ,2) =
2

261. 2. Cas d’une fonction de deux variables
f (x , y)
f’x (x , y)
f’y (x , y)
'
xf ( x, y)
e( f , x) = x
f ( x, y)
'
yf ( x, y)
y
e( f , y) =
f ( x, y)
Elasticité partielle
par rapport à x
Elasticité partielle
par rapport à y

262. Exemples
1.
f (x, y) =5x2 y −xy2 :
x
'
f x ( x, y) =10 xy − y 2
'
xf ( x, y) 10x 2 y − xy 2
e( f , x) = x
=
2
2
f ( x, y) 5x y − xy

263. f (x, y) =5x2 y −xy2
y
'
f y ( x, y) =5x2 −2xy
'
yf ( x, y)
2
2
5x y −2xy
y
e( f , y) =
=
2
2
5x y − xy
f ( x, y)

264. Ainsi
f (x, y) =5x2 y −xy2
y
x
2
2
2
2
10x y − xy e( f , y) = 5x y −2xy
e( f , x) =
2
2
2
2
5x y − xy
5x y − xy
Exemple : x = 1 ; y = 1
e( f , x) =9 / 4 et e( f , y) =3/ 4

265. Exemples
2.
f (x, y) = x0,01y0,99 :
x
'
f x ( x, y) = 0,01x−0,99 y0,99
'
xf ( x, y) 0,01x 0,01 y 0,99
e( f , x) = x
=
=0,01
0,01 0,99
x
y
f ( x, y)

266. f (x, y) = x0,01y0,99
y
'
f y ( x, y) = 0,99x0,01y −0,01
'
0,01 0,99
yf ( x, y)
0,99x
y
y
e( f , y) =
=
=0,99
0,01 0,99
x
y
f ( x, y)

267. Ainsi
0,01y0,99
f (x, y) = x
x
e( f , x) =0,01
y
e( f , y) =0,99

268. D’une manière générale
α yβ
f (x, y) =kx
x
e( f , x) =α
y
e( f , y) = β

269. Séance n° 9

270. 4. Quelques définitions
c) Différentielle totale

271. Définition
La différentielle totale de f au point
(x0 , y0) avec les accroissements dx et dy
est la quantité :
'
'
df ( x , y ) = f x ( x0, y0)×dx + f y ( x0, y0)×dy
0
0

272. Exemple
f (x, y) = x2 y + xy2 = xy(x + y)
Calculer la différentielle totale de f au
point (20,30) avec les accroissements
dx = 1 et dy = -1

273. Réponse
'
'
df (20,30) = f x (20,30)×1+ f y (20,30)×(−1)
Or :
'
'
 f,x ( x, y) = 2xy + y2 ⇒ f x (20,30) = 2100
'
'
 f y,( x, y) = x2 +2xy ⇒ f y (20,30) =1600
⇒df (20,30) = 2100×1+1600×(−1) =500

274. Interprétation
(x0+dx,y0+dy)
dy
(x0,y0)
dx
Question :
Lorsque x subit une légère variation dx «ou
x
» ∆(on passe de x0 à x0 +dx) et y subit une
légère variation dy «ou »∆y passe de y0 à
(on
y0 +dy) , de combien varie la fonction f «
∆f =?
»?

275. Réponse
1. Calcul direct :
∆f = f ( x0 +dx, y0 +dy) − f ( x0, y0)
2. Valeur approchée :
∆f ≅ df
(x , y )
0
0

276. Exemple
Soit la fonction U (appelée fonction d’utilité)
donnée par :
U ( x, y) = x1/ 3 y2 / 3
 Calculer U(x,y) pour x=8 et y=1
 De combien varie la fonction d’utilité U
si x augmente de dx=0,1 et y diminue de
dy=0,01
(Utiliser deux méthodes)

277. Réponse
1. Calcul direct :
On a :
x0 =8 ; y0 =1 ; dx =0,1 ; dy =−0,01
∆U =U ( x0 + dx; y0 + dy) −U ( x0; y0 )
=U (8,1;0,99) −U (8;1)
=3 8,1×3
2
0,99 −2 = −0,00511..

278. Réponse
2. Valeur approchée :
∆U ≅ dU (8,1)
dx =0,1
avec les accroissements
dy = −0,01





'
dU (8,1) =U x (8,1)×0,1+U 'y (8,1)×(−0,01)

279.  U ' ( x, y) = 1 x − 2 / 3 y 2 / 3 ⇒U ' (8,1) =
x
x
1
3
12
;
'y ( x, y) = 2 x1/ 3 y −1/ 3 ⇒U 'y (8,1) = 4
U
3
3;

dU (8,1) =1/12×(0,1) + 4 / 3×(−0,01)
Donc :
C’est-à-dire :
dU (8,1) = −0,005
On obtient ainsi :
∆U ≅ −0,005

280. Quelques Interprétations
Economiques
Variation &
Variation relative

281. Exemple
Le salaire S d’un employé a été
augmenté de 1300 DH
On parle ici de variation du Salaire :

∆S =1300
Le nouveau salaire est :
S '= S +∆S = S +1300

282. Exemple
Le salaire S d’un employé a été
augmenté de 5% : ⇒∆S =5%×S
On parle ici de variation relative du
Salaire :
∆S

S
=5%
Le nouveau salaire est :
S '= S +∆S = S +0,05×S =1,05×S

283. A. Cas d’une fonction
« économique » d’une variable
 Variation de f :
On rappelle que :
f '( x0 ) = lim
x→ x
f ( x) − f ( x )
0
x − x0
0

284. Lorsque x → x0 ; f ( x) → f ( x0 ) (f est continue)
On note : df = f ( x) − f ( x0 ) et dx = x − x0
que l’on appelle respectivement différentielle
de f et différentielle de x, on a donc :
df
f '( x) =
dx
ou encore
df = f '( x)×dx
Exemples :
1
dx ;
• f ( x) = x ⇒ df =
2 x
1
1 .
• f ( x) = ⇒ df = − dx
2
x
x

285. Notations
dx
: Variation infiniment petite de x
df
: Variation infiniment petite de f
∆x : Variation très petite « faible» de x
∆f
: Variation très petite « faible» de f

286. En pratique
si la variation ∆x que subit x est faible :
la variation subit par la fonction f est faible
et on a :
∆f ≅ f '(x)×∆x
Remarque : dans la formule
nous avons remplacé :
dx par ∆x
et
df
df = f '( x)×dx
par
∆f

287. Exemple
 Le coût global de la fabrication d’un
bien en quantité x est donnée par la
formule :
C(x) = 250 − x2
Pour une quantité x=10 (par exemple) :
C(10) = 250 −100 =150

288.  Calculons l’écart (de 2 façons différentes)
résultant d’une augmentation ∆x =1
1) Calcul direct :
C(11)=250−112 =250−121=129
donc
∆C = C(11) − C(10) =129 −150 = −21

289. 2) Valeur approchée : en appliquant la
formule :
∆C ≅ C'( x)× ∆x
On obtient :
C'( x) = −2x ⇒ ∆C ≅ (−20)×(1)
∆C ≅ −20

290. A retenir
• Si x subit une faible variation ∆x , une
valeur approchée de la variation ∆f de f
est donnée par la formule :
∆f ≅ f '(x)×∆x

291. 
On a :
Variation relative
∆f ≅ f '( x)× ∆x ⇔ f '( x) ≅
∆f
∆x
 L’élasticité de f au point x est :
∆f
∆f
x
xf '( x)
∆x ⇒e( f , x) ≅ f
e( f , x) =
≅
∆x
f ( x) f ( x)
x

292. Elasticité de f au point x :
∆f
f
e( f , x) ≅
∆x
x
⇔
∆f ≅ e( f , x)× ∆x
f
x
∆f
représente la variation relative de f
f
∆x représente la variation relative de x
x

293. Exemple
f(x) représente une fonction économique
dépendant de la quantité x d’un bien
distribué.
 On suppose connaitre la valeur de f pour
une quantité x=1000 et que l’élasticité en
x=1000 est : e(f,1000) = 5.

294. Exemple

La quantité distribuée à baissé de 2%
(980 unités ont été distribuées au lieu de 1000),
cela entrainera une variation relative de f :
∆f ≅ e( f , x)× ∆x =5×−2% = −10%
f
x
f a baissé d’environ 10%

295. A retenir
• Si x subit une faible variation relative
, une valeur approchée
∆x/ x
de la variation relative de f est
donnée par la f
∆formule :
∆x
f
≅e( f , x)×
x
e( f , x) désigne l’élasticité de f au point x

296. B. Cas d’une fonction
« économique » de deux
variables

Variation de f :
Nous avons vu que :
∆f ≅ df
( x0 , y0 )
C’est-à-dire :
'
'
∆f ≅ f x ( x0, y0 )×dx + f y ( x0, y0 )×dy

297. En pratique : si la variation ∆x que subit
x est faible et la variation ∆y que subit
y est faible : la variation subit par la
fonction f est faible et on a :
'
'
∆f ≅ f x ( x0, y0 )×∆x + f y ( x0, y0 )×∆y
Voir exemple précédent
« paragraphe 4 c) : différentielle totale »

298. A retenir
• Si x subit une faible variation ∆x
et y subit une faible
∆y
variation
, une valeur
approchée de la variation de f est
donnée par la formule :
'
'
∆f ≅ f x ( x0, y0 )×∆x + f y ( x0, y0 )×∆y

299. 
Variation relative
'
'
On a : ∆f ≅ f x ( x, y)×∆x + f y ( x, y)×∆y
 En divisant par f(x,y) :
' ( x, y)
f
' ( x, y)
f
∆f ≅ x
y
×∆x +
×∆y
f
f ( x, y)
f ( x, y)

300. On fait apparaître les variations
relatives de x et de y :

' ( x, y)
xf
' ( x, y)
yf
∆f ≅ x
∆x + y
∆y
×
×
f
f ( x, y) x
f ( x, y) y
∆f ≅ e( f , x)× ∆x +e( f , y)× ∆y
⇒
f
x
y

301. Variation relative de f
∆f ≅ e( f , x)× ∆x +e( f , y)× ∆y
f
x
y
∆f
représente la variation relative de f
f
∆x et ∆y représentent les variations
y
x
relatives
de x et de y
e( f , x) et e( f , y) représentent les
élasticités
à x et à y
partielles par rapport

302. Exemple
f(x,y)
représente une fonction
économique
dépendant de deux
quantités x et y de deux biens fabriqués.
 On suppose connaitre la valeur de f pour
une quantité x=1000 et y=500. Supposons
aussi que les élasticités partielles en x=1000
et y=500 sont : e(f , x) = 5 et e(f , y) = 3

303. Exemple
 Suite à un incident technique, la fabrication
des deux biens a légèrement varié : x a
diminué de 4% et y a augmenté de 5%.
Quelle variation cela entrainera sur la fonction
économique f ?
∆f ≅ 5×(−4%) +3×5% = −5%
f
la fonction économique f subira une baisse
d’environ 5%

304. A retenir
• Si x subit une faible variation relative
et y subit une faible
∆x/ x
variation relative
, une valeur
∆y/ y
approchée de la variation relative de f
est donnée par la formule :
∆f ≅ e( f , x)× ∆x +e( f , y)× ∆y
f
x
y

305. Fin de
l’interprétation
Economique
Suite du Cours

306. Séance n° 10

307. 4. Quelques définitions
d) Hessien de f
Rappel : déterminant d’ordre 2
a
b
c
=ad −bc
d

308. Définition
Le Hessien de f au point (x , y)
est la quantité :
''
f xx ( x, y)
H (x, y) =
f
''
f yx (x, y)
''
f xy (x, y)
''
f yy (x, y)

309. Exemple
 Soit la fonction
f (x, y) = x2 y − xy3
Calculer le Hessien de f aux points (0;0),
(1;2) et (-2;1)

310. f (x, y) = x2 y − xy3
y
x
'
f x ( x, y) = 2xy − y3
y
x
'
f y ( x, y) = x 2 −3xy 2
x
y
''
''
f xy ( x, y) = f yx ( x, y) = 2x −3 y 2
''
f xx ( x, y) = 2 y
''
f yy ( x, y) = −6xy

311. Donc Le Hessien de f au point (x , y) est
donné par :
H (x, y) =
f
2y
2x −3 y 2
2x −3 y 2
−6xy

312. Ainsi
0
 H (0,0) =
f
0


4
H (1,2) =
f
−10
2
H (−2,1) =
f
−7
0
=0 −0 =0
;
0
−10
−12
−7
12
= −48 −100 =;−148
= 24 −49 = −25
;

313. 5. Optimisation
Ou
Recherche d’Extrema

314. Remarque
Extrema
Ou
Extrémums
Maximum
« MAX »
Ou
Minimum
« MIN »

315. Problème
Soit f(x , y) une fonction de deux variables
définie sur un domaine D
( ( x, y)∈D ⊂ IR2)

On cherche les couples (x , y)
qui rendent f maximale ou minimale

316. Extrémum local ou global
Plus grand
Plus petit
Max
global
Max
local
Min
local
Max
local
Min
local
Min
global
Max
local

317. Un maximum global (s’il existe) est
un point (x0,y0) du domaine D qui vérifie :

∀(x, y)∈D : f ( x, y) ≤ f (x0, y0)
Un minimum global (s’il existe) est
un point (x0,y0) du domaine D qui vérifie :

∀(x, y)∈D : f ( x, y) ≥ f (x0, y0)

318. a) Extrémums ”locaux” libres
On checrche les extrémums “locaux”
de la fonction f sachant qu’il n y a aucune
contrainte sur les variables x et y :
on dit que les variables x et y sont
indépendantes ou libres

319. 
On parle alors d’éxtrémums libres
de la fonction f sur le domaine D

320. Méthode à suivre
I.
Etape 1 : Recherche des candidats
Remarque : On dit aussi points critiques ou
points stationnaires

Ce sont les couples (x , y) solutions
du système :
'
f x(x, y) =0
S: '
f y(x, y) =0












321. On doit résoudre le système S “ étape un
peu difficile !” et donner ses solutions :
(x0 , y0) ; (x1 , y1) ; (x2 , y2) ; etc...
 Les couples (x0
, y0) ; (x1 , y1) ; (x2 , y2)
... sont les candidats ( ...pour être
extrémums), ou les points critiques de la
fonction f
(on dit aussi : points stationnaires de f)

322. Etape 2
Nature des candidats
II.
Max
Min

323. Etape 2
Nature des candidats
II.
Point-selle
Ni Max
Ni Min

324. Etape 2
Nature des candidats
II.
Col
Ni Max
Ni Min

325. Etape 2 : Nature des candidats
 On calcule le Hessien de f pour chaque
candidat.
Soit (x0 , y0) un candidat issu de l’étape 1 :
''
f xx (x0, y0)
H (x0, y0) =
f
''
f yx (x0, y0)
''
f xy (x0, y0)
''
f yy (x0, y0)

326. Etape 2 : Nature des candidats
Si Hf (x0 , y0)
<0⇒pas d’extrémum en (x
0
, y0)
« Ni Max ni Min »
Il s’agit d’un Col ou un point-selle en (x0 , y0)
Si Hf (x0
>0⇒ f présente un extrémum
,y)
0
en (x0 , y0)

327. Pour savoir s’il s’agit d’un Max ou d’un Min, on
regarde le signe de la dérivée seconde par
rapport à x (ou par rapport à y) :
 Si
''
f xx(x0, y0)<0 :
f présente un Maximum en (x
0
, y0)
''
 Si f xx(x0, y0) >0 :
f présente un Minimum en (x
0
, y0)

328. 3ème cas : On ne peut pas conclure
 Si Hf (x0 , y0) = 0 :
Dans ce cas, on ne peut rien conclure
Remarque : Dans ce cas, on peut faire appel à
d’autres méthodes : Des estimations locales
de la fonction au voisinage du point (x0 , y0)
par exemple. Voir «TD : Partie 2 - Exercice 3»

329. Exemple 1
Soit la fonction :
f ( x, y) = −3x2 −4 y 2 −3xy +69x +93 y
 Trouver les extrémums « locaux » de
la fonction f

330. Réponse
I.
Etape 1 : Recherche des candidats

On doit résoudre le système :
'
f x(x, y) =0 ⇔ −6x −3y +69 =0
S: '
−8 y −3x +93= 0
f y(x, y) =0




















6x +3y = 69 ⇔ x = 7
⇔
3x +8 y =93
y =9














Nous avons un seul candidat : le couple (7 , 9)

331. Réponse
II. Etape 2 : Nature des candidats
On calcule le Hessien de f au point (7 , 9) :
''
f xx (x, y)
H (x, y) =
f
''
f yx (x, y)
−6
⇒H ( x, y) =
f
−3
''
f xy (x, y)
''
f yy (x, y)
−3
=39
−8

332. Réponse
Le Hessien de f ne dépend ici de (x , y), nous
avons alors au point (7 , 9) :
⇒H (7,9) =39 >0
f
f présente donc un extrémum au point (7 , 9)
Pour savoir s’il s’agit d’un Max ou d’un Min, on
regarde le signe de la dérivée seconde par
rapport à x :

333. Réponse
''
''
f xx (x, y) =−6 ⇒ f xx (7,9) =−6 <0
f présente donc un Maximum « local » au
point (7 , 9)

La valeur de ce maximum est :
f (7,9) =660

334. Exemple 2
Soit la fonction :
f ( x, y) =3xy − x3 − y3
 Trouver les extrémums « locaux » de
la fonction f

335. I.
Etape 1 : Recherche des candidats

On doit résoudre le système :
'
f x(x, y) =0
3( y − x2) = 0
⇔
S: '
3(x − y2) = 0
f y(x, y) =0































2
y = x2 ⇔ y = x
⇔
2 2
4
x = y2
x = (x ) = x










336. Etape 1 : Recherche des candidats

2











y = x2 ⇔ y = x
⇔
S
3
x − x4 = 0
x(1− x ) = 0
















⇔ y=x
2
⇔ x = 0..ou.. x =1
y =0
y =1
x = 0..ou..x =1














Nous avons ici deux candidats (0 , 0) et (1, 1)

337. Etape 2 : Nature des candidats
On calcule le Hessien de f aux points (0,0),
(1,1) :


H f ( x, y) =
H f (0,0) =
H f (1,1) =
0
3
3
3
−6 y
= −9 <0 ⇒
3 0
−6 3
3
−6x
−6
pas d’extrémum
en (0,0)
=36 −9 = 27 >0 ⇒
pas d’

338. Réponse
On regarde le signe de la dérivée seconde de f
par rapport à x au point (1 , 1) :
''
''
f xx (x, y) =−6x ⇒ f xx (1,1) =−6 <0
f présente donc un Maximum « local » au
point (1 , 1)

La valeur de ce maximum est :
f (1,1) =1

339. Séance n° 11
« Dernière Séance »

340. b) Extrémums ”locaux” liés
On checrche les extrémums “locaux”
de la fonction f sachant que les variables
x et y sont liées par une équation
appelée “contrainte”
Contrainte :
g (x, y) =0

341. 
On parle alors d’éxtrémums de
la fonction f sur le domaine D liés par la
contrainte g ( x, y) =0
Le problème est plus simple que
celui des extrémums libres :


342. z
Max
Max
Min
Surface
z=f(x , y)
x
Df
y
(x , y) vérifiant la contrainte

343. z
Max
Max
Min
x
y
g ( x, y) = 0

344. Deux méthodes :
I.
Méthode de substitution
Ou
II. Méthode du multiplicateur
de Lagrange

345. I.
Méthode de substitution

g
A partir de la contrainte( x, y) =0
,
on exprime y en fonction de x (ou x en
fonction de y) et on remplace dans
la fonction f(x , y)

On obtient alors une fonction d’une
variable réelle :
on cherche ses extrémums

346. Exemple
Chercher les extrémums de la fonction :
f ( x, y) =3xy − x2 − y 2
Sous la contrainte
x + y =2

347. Réponse
On pose :
g (x, y) = x + y −2
« contrainte »

g (x, y) =0 ⇔ y, =2 − x
on remplace y par sa valeur dans f (x , y) :

348. Réponse
f (x, y) = f (x,2 − x)
=3x(2 − x) − x2 −(2 − x)2
= −5x2 +10x −4 =h( x)
On obtient une fonction d’une variable : h(x)

349. Réponse
On cherche les extrémums de la fonction h(x) :

h'( x) = −10x +10 =10(1− x)
x
−∞
h’(x)
1
+ 0
1
_
+∞
h(x)
−∞
Max
−∞

350. Réponse
 La fonction
h présente un extrémum en x=1
x =1
x =1⇒ y = 2 − x =1⇒
y =1





Conclusion
La fonction f présente un seul extrémum sous
la contrainte x + y = 2 : un Maximum en (1 , 1)
 La valeur de ce maximum est : f (1,1) =1

351. Remarque
On utilise la méthode de substitution
lorsque la contrainte g permet d’exprimer
facilement y en fonction de x (ou x en
fonction de y)

352. II. Méthode de Lagrange
 On intègre la contrainte dans le
problème en considérant la fonction de
Lagrange « à 3 variables » suivante :
L(x, y,λ) = f (x, y) +λg (x, y)
λest le multiplicateur de Lagrange

353. II. Méthode de Lagrange
 On cherche alors les extrémums « libres »
de la fonction L :
 Deux étapes :
 Recherche des candidats
 Nature des candidats
Problème à 3 variables !!

354. Etape 1 : Recherche des candidats
 On commence par résoudre le système :
S:

















L'x(x, y,λ) =0
L'y(x, y,λ) =0
'
Lλ (x, y,λ) =0
Les solutions (x1 , y1 , λ1 ) ; (x2 , y2 , λ2) ...
du système S sont les candidats

355. Etape 2 : Nature des candidats
 On calcule le Hessien de L pour chaque
candidat.
Soit (x1 , y1 , λ1 ) un candidat issu de l’étape 1
HL (x1 , y1 , λ1 )

356. ''
Lxx
''
H ( x1, y1,λ1) = L yx
L
''
L
λx
''
Lxy
''
L
''
L
xλ
''
L
''
L
''
L
yy
λy
Calculé au point (x1 , y1 , λ1 )
yλ
λλ

357.  Si HL (x1 , y1 , λ1)
>0
f présente un Maximum en (x
 Si HL (x1 , y1 ,
1
, y1)
1
, y1)
<0
)
λ1
f présente un Minimum en (x

358. 3
ème
cas : On ne peut pas conclure
 Si HL (x1 , y1 , λ1) = 0
Dans ce cas, on ne peut rien conclure

359. Exemple
Soit la fonction :
f ( x, y) = x + y +5
 Chercher les extrémums de
contrainte : x2 + y 2 =1
f sous la

360. Réponse
On pose :
g ( x, y) = x2 + y 2 −1
 La fonction de Lagrange est donnée par :
L(x, y,λ) = f ( x, y) +λg (x, y)
= x + y +5+λ(x2 + y 2 −1)

361. I.
Etape 1 : Recherche des candidats

On doit résoudre le système :
L'x(x, y,λ) =0
1+ 2λx = 0
L'y(x, y,λ) =0 ⇔ 1+ 2λy =0
S:
x2 + y2 −1=0
' (x, y,λ) =0
Lλ
λ = −1/ 2x
⇔ λ = −1/ 2 y
x2 + y2 −1=0












































362. 
Egalité des deux premières
équations :
λ = −1/ 2x = −1/ 2 y⇒ x = y
On remplace dans la 3ème équation :
2 + y2 =1⇔ 2x2 =1⇔ x = ± 2
x
2

363. 2 ⇒ y= 2
 x=
2
2
2 ⇒ y =− 2
 x=−
2
2
1 =− 2
λ
car x=y et= −
2x
2
1= 2
λ
et = −
2x 2

364. Nous avons donc deux candidats :

2 , 2)
2
(
avec λ = −
2 2
2
et
2 ,− 2 ) avec λ = 2
(−
2
2 2

365. Etape 2 : Nature des candidats
 Calcul du Hessien de L :
2λ
λ1
H ( x, y,λ) = 0
L
2x
0
2λ
2y
2x
2y
0
En développant suivant la 1ère ligne par exemple :

366. On obtient :
2λ
H ( x, y,λ) = 2λ
L
2y
2y
0
+2x
0
2λ
=−8λy 2 −8λx2
=−8λ(x2 + y 2)
2x
2y

367. Ainsi :
2 , 2 ) = 8 2 >0
 H (
:
L 2 2
2
Maximum en ( 2 / 2, 2 / 2)
2 ,− 2 ) = −8 2 <0
 H (−
:
L 2
2
2
Minimum en (− 2 / 2,− 2 / 2)

368. Conclusion
La fonction f présente deux extrémums
x2 +
sous la contrainte y 2 =1
:
2 2
 Un Maximum en ( , )
2 2
 Un Minimum en (−
2
2
,−
2
2
)

369. 6. Fonction composée

370. Cas simple
« Une variable »
Exemple
On considère la fonction à deux variables
suivante : f ( x, y) =3xy − x2 − y 2
On pose : F (t) =
F'
Calculer(t)
f (t +1,t 2 −2)

371. Réponse
1)
Méthode directe :
On calcule F (t) puis on dérive :
F (t) = f (t +1,t 2 −2)
= 3(t +1)(t 2 −2) −(t +1)2 −(t 2 −2)2
= −t 4 +3t 3 +6t 2 −8t −11
⇒ F '(t) = −4t 3 +9t 2 +12t −8

372. 2) Formule de dérivation
On pose :
avec
F (t) = f (u(t),v(t))
u(t) =t +1 et v(t) =t 2 −2
 On a alors :
'
'
F '(t ) = f x (u(t ),v(t ))×u'(t ) + f y (u(t ),v(t ))×v'(t )

373. Cette formule de dérivation fait intervenir
les dérivées partielles de f :
f ( x, y) =3xy − x2 − y 2
x
'
f x ( x, y) =3 y −2x
y
'
f y ( x, y) =3x −2 y

374. Ainsi :
'
 f x (u(t ),v(t )) = 3v(t ) −2u(t ) = 3t 2 −2t −8 ,
'
 f y (u(t ),v(t )) = 3u(t ) −2v(t ) = −2t 2 +3t +7 ,
On applique la formule :
'
'
F '(t ) = f x (u(t ),v(t ))×u'(t ) + f y (u(t ),v(t ))×v'(t )
= (3t 2 − 2t −8)×1+ (−2t 2 + 3t + 7) × 2t
= −4t 3 +9t 2 +12t −8

375. A retenir
On considère la fonction à une variable
définie par : F (t) = f (u(t),v(t))
où f est une fonction de deux variables
notées x et y : (x , y)
f (x , y)
 On a alors :
'
'
F '(t ) = f x (u(t ),v(t ))×u'(t ) + f y (u(t ),v(t ))×v'(t )

376. « Fin du Cours »