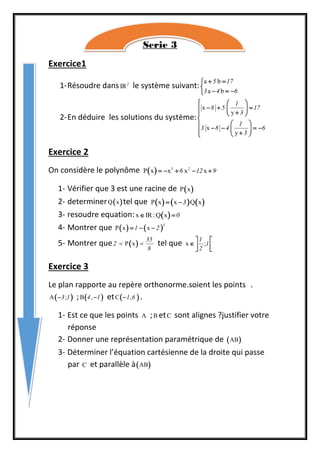
Le document présente une série d'exercices mathématiques, notamment la résolution d'un système d'équations et l'analyse d'un polynôme. Il aborde également des concepts géométriques tels que l'alignement de points et l'équation de droites dans un plan. Les exercices incluent des vérifications de racines, la détermination de polynômes associés et des représentations paramétriques.

1. Serie 3
Exercice1
1-Résoudre dansIR2
le système suivant:
a b
a b
 

  
5 17
3 4 6
2-En déduire les solutions du système:
x
y
x
y
  
    
  

        
1
8 5 17
3
1
3 8 4 6
3
Exercice 2
On considère le polynôme  P x x x x    3 2
6 12 9
1- Vérifier que 3 est une racine de  P x
2- determiner  Q x tel que      P x x Q x 3
3- resoudre equation:  x IR :Q x 0
4- Montrer que    P x x  
3
1 2
5- Montrer que  P x
35
2
8
tel que x ;
 
   
1
1
2
Exercice 3
Le plan rapporte au repère orthonorme.soient les points .
 A ;3 1 ;  B ,4 1 et  C ,1 6 .
1- Est ce que les points A ;B etC sont alignes ?justifier votre
réponse
2- Donner une représentation paramétrique de  AB
3- Déterminer l’équation cartésienne de la droite qui passe
par C et parallèle à AB