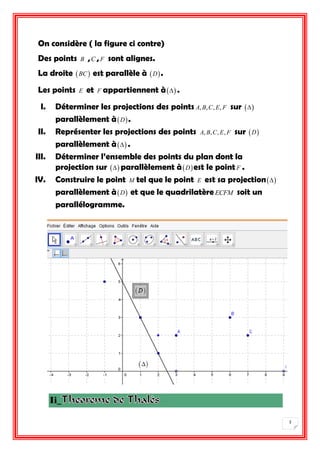
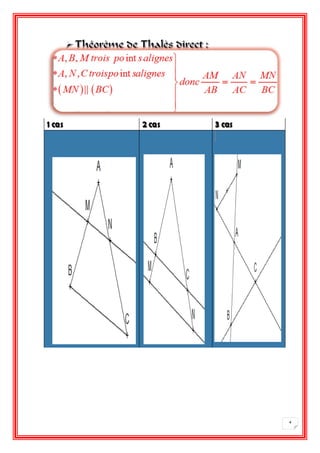
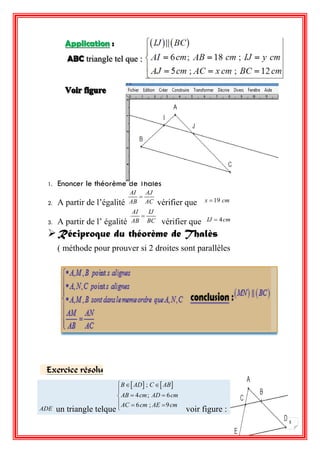
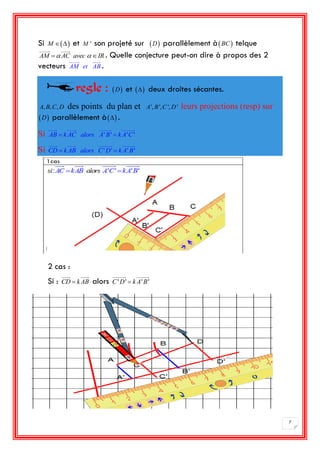
Le document aborde les compétences géométriques, en détaillant le théorème de Thalès et les projections de points sur des droites. Il propose des applications et exercices illustrant la conservation du coefficient de colinéarité lors de projections parallèles. Des cas particuliers et des constructions géométriques sont également explorés pour renforcer la compréhension des concepts.

1. 1
Chapitre 5
Compétences exigibles
i. Définition
ii. Théorème de Thales
iii. Conservation de coefficient de colinéarité de 2
vecteurs
Activite1
On suppose les fils des rayons du soleil prennent la direction de la
droiteD et la droite  représente la surface du sol. L’ombre du
point A sur le sol est le point A' l’intersection de la droite  avec la
droite passant par A et parallèlement à la droiteD .( voir figure ci
contre).
2_ Vocabulaire
B

2. 2
 Le point A' est appelé projection du point A sur 
parallèlement àD .
 B : B est son propre projeté sur  parallèlement àD .
3_ Définition :
Soient D et  deux droites secantes et M un point du plan tel
que M  .
Dire que le point M 'est la projection du point M sur
parallèlement àD veut dire :M 'et MM ' D .
Cas particulier :
Si D   : A' est la projection orthogonale de A
sur  .
4_ Application :

3. 3
On considère ( la figure ci contre)
Des points B ,C , F sont alignes.
La droite BC est parallèle à D .
Les points E et F appartiennent à .
I. Déterminer les projections des points A, B,C, E, F sur 
parallèlement àD .
II. Représenter les projections des points A, B,C, E, F sur D
parallèlement à .
III. Déterminer l’ensemble des points du plan dont la
projection sur  parallèlement àDest le point F .
IV. Construire le point M tel que le point E est sa projection
parallèlement àD et que le quadrilatère ECFM soit un
parallélogramme.
Ii_

4. 4
Soient Regarde figures :

5. 5
Application :
ABC triangle tel que :
1. Enoncer le théorème de Thalès
2. A partir de l’égalité
AI AJ
AB AC

vérifier que x 19 cm
3. A partir de l’ égalité
AI IJ
AB BC

vérifier que IJ  4cm
 Réciproque du théorème de Thalès
( méthode pour prouver si 2 droites sont parallèles
Exercice résolu
ADE un triangle telque
  ;  
4 ; 6
6 ; 9
B AD C AB
AB cm AD cm
AC cm AE cm
  

  
  
 voir figure :

6. 6
Montrons que : BC DE
Ona : donc
ona :
donc : BC ED d’après la réciproque du théorème de Thalès
exercice ; (voir figure ci contre) montrer que BC DE
III_
Activité :
Soient D et  deux droites sécantes en A . Les points M, N,P
appartiennent à talque : AM  2AC ; AN  5AC ; AP  3AC et les
pointsM ', N ', P' sont les projections respectives des pointsM, N,P sur 
parallèlement àBC .
1. Faire une figure géométrique
2. En utilisant le théorème de Thalès établir que :
' ' '
2 ; 5 ; 3
AM AN AP
AB AB AB
  
3. En deduire que AM'  2AB ; AN'  5AB ; AP'  3AB
, ,
, ,
, , ; ;
2
3
A B D sont alignes
A C E sont alignes
A B D sont dans lememeordre que A C E
AB AC
AD AE






  


7. 7
Si M  et M ' son projeté sur D parallèlement àBC telque
AM  AC avec IR . Quelle conjecture peut-on dire à propos des 2
vecteurs AM et AB .
R rregle : D et  deux droites sécantes.
A, B,C,D des points du plan et A',B',C ',D' leurs projections (resp) sur
D parallèlement à .
Si AB  kAC alors A'B'  kA'C'
Si CD  kAB alors C'D'  kA'B'
2 cas :
Si : CD  kAB alors C'D'  kA'B'

8. 8
Exercice résolu :
Soit ABC un triangle et M AB tel que 1
3
AM  AB et N le projeté de
M sur  ACparallèlement à BC .
Montrons que : 1
3
AN  AC
 A est sa propre projection sur  ACparallèlement àBC
 N est la projection de M sur  ACparallèlement àBC
 C est la projection de B sur  ACparallèlement àBC
Et comme 1
3
AM  AB alors 1
3
AN  AC car la projection conserve le
coefficient de colinéarité.

9. 9
EXERCICE 1 :
ABC un triangle et E un point vérifiant EA EB  0
1. Exprimer AE en fonction de AB
2. Soit F le projeté de E sur  AC
parallèlement à BC
. Montrer que
4
5
AF  AC
EXERCICE 2 :
ABCDest un trapèze tel que  AB CD
et AB CD. I le point d’intersection de
ses diagonales
- J est le projeté de I sur  AB
parallèlement à BC
.
- K est le projeté de I sur  AD
parallèlement à BC
.
1. Comparer
AJ
AB et
AI
AC
2. Montrer que  JK BD
.
EXERCICE 3 :
ABC un triangle et A' le milieu de BC
. Soit D un point tel que
3
'
4
AD  AA
.
1. Construire les points E et F tel que E est le projeté de D sur BC
parallèlement à  AB
et F est le projeté de D sur BC
parallèlement à
 AC
.
2. Montrer que
3
'
4
BE  BA
et
3
'
4
CF  CA

10. 10
3. En déduire que A est le milieu de EF

11. 11