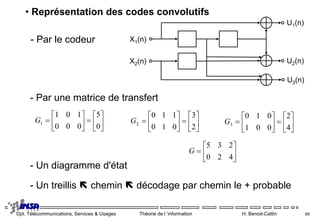
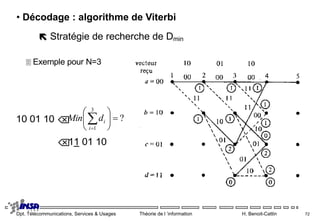
Le document aborde la théorie de l'information en télécommunications, notamment le codage de canal et la détection/correction d'erreurs. Il explique les concepts de taux d'erreur, codes linéaires, codes de Hamming, et codes cycliques, tout en détaillant les matrices de contrôle et de génération. L'accent est mis sur les méthodes permettant de détecter et de corriger les erreurs de transmission.

1. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 40
• 1. Introduction
• 2. Sources discrètes & Entropie
• 3. Canaux discrets & Capacité
• 4. Codage de source
• 5. Codage de canal
• 6. Cryptographie
• 7. Conclusion
Plan

2. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 41
5. Codage de canal
Codeur de canal  introduire une redondance utilisable
 Détecter et/ou corriger les erreurs de transmission

3. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 42
• Théorème des canaux à perturbation (codage de canal)
" Pour une source à débit d'information de R bit/s et un canal de
capacité C bit/s, si R<C, il existe un code ayant des mots de
longueur n, de sorte que la probabilité d'erreur de décodage pE
vérifie :
)
(
.
2 R
E
n
E
p 
 "
Rq1 : un résultat inatendu !
Rq2 : existance ss méthode ...
Rq3 : à pE constant, n augmente si R
tend vers C.
Rq4 : en pratique, si R<0.5 C, des
codes existent avec pE faible.

4. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 43
• Taux d'erreur
transmis
bits
de
Nombre
erronés
bits
de
Nombre
Te 
011001001001100100101001010  011001101100101101000010
125
.
0
24
3 

e
T

• Probabilité d'erreur
r
n
r
r
n
n
erreurs
r p
p
C
P 

 )
1
.(
.
/
n
corrects
bits
n p
P )
1
( 


5. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 44
• Taux de codage
n
k
R 
- k taille du mot d ’information (avant codage)
- n taille du mot-code (après codage)

6. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 45
• Détection et correction d'erreurs
 Détection par écho
 Détection par répétition
 Détection par bit de parité
 Détection par code
 Détection et correction par code

7. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 46
• Détection d'erreurs par bit de parité (caractère)
 VRC (Vertical Redundancy Check)
 Asynchrone
 LRC (Longitudinal Redundancy Check)
 Synchrone

8. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 47
• Codes détecteur et/ou correcteur
 Codes linéaires
• Codes groupes
Parité, Code de Hamming
• Codes cycliques
CRC/FCS, code BCH, Golay
 Codes convolutifs
Algorithme de Viterbi

9. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 48
Codes linéaires
CS CC Canal
P
DC
i v v’
]
[
]
....
....
[ 2
1
2
1 i
c
a
a
a
a
a
a
v n
m
m
m 
 

[ c ] : m symboles de contrôle
[ i ] : k =n-m symboles d'information
 
n



 .....
.
2
1
 
 





 i
i
i
i v
v
v
v







sinon
0
position
ième
la
à
erreur
si
1
i

• Mot-code : v
• Mot-erreur : 
• Notations

10. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 49
• Distance de Hamming
)
(
....
)
(
)
(
)
,
( 2
2
1
1 jn
in
j
i
j
i
j
i a
a
a
a
a
a
v
v
D 






 Le nombre de coordonnées par lesquels les 2
mots diffèrent
• Propriétés des codes linéaires
Les symboles de contrôle sont obtenus par une combinaison
linéaire des symboles d ’information.
 un code linéaire contient v=[0 0 …0]
• Code systématique
Les symboles d ’information et de contrôle sont séparés.

11. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 50
• Illustration spatiale : modèle code groupe
 W = ensemble des N = 2n
mots
 V = ensemble des S = 2k
mots ayant un sens (mot-code) W
V
• Un mot = un vecteur dans un espace à n dimensions !
w=[a1 a2 ... an]

12. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 51
i
i W
v Région
 Région 0 
W équidistant
Détection et correction  si Wi grand
Ex Hamming(S4
)
• Capacité de détection et région de décision
 Détecter d erreurs 
Dmin= d+1
 Corriger e erreurs Dmin= 2e+1
 Corriger e & détecter d erreurs Dmin= 2e + d + 1
Théorème de Hamming

13. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 52
• Principe de détection et correction
k
i S
i
v 2
à
1
pout tout
0
)
( 



erreur
d'
pas
alors
0
)
(
Si i 




 i
i v
v
v

erreur
d'
détection
0
)
(
Si 



 z
vi


 D(z)
connu
est
z
Si
erreur
d'
correction



 i
i v
v 

D
:
opérateurs
Deux 

14. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 53
• Décodage et matrice de contrôle
 













mn
2
m
1
m
n
2
22
21
n
1
12
11
h
...
h
h
...
...
h
h
h
h
...
h
h
H
Soit H(m,n) la matrice de contrôle,













m
1
T
z
:
z
v
.
H
z
Soit z le syndrome (ou correcteur),
 
n
2
1 a
...
a
a
v 
Si z=[0] pas d ’erreur, sinon erreur et +- correction

15. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 54
• Codage et matrice génératrice
G
.
i
v 
Soit G(k,n) la matrice génératrice,
0
H
.
G t












:
A
:
I
:
G m
,
k
k











:
I
:
A
:
H m
m
,
k
t
 
k
2
1 i
...
i
i
i 
 













kn
2
k
1
k
n
2
22
21
n
1
12
11
g
...
g
g
...
...
g
g
g
g
...
g
g
G
Les matrices H et G sont liées par :
et peuvent se mettrent sous la forme systématique

16. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 55
• Exemple k=2, m=1, n=3
 
1
1
1
]
H
[ 
   
0
0
0
1
0
1
1
1
0
0
0 







   
1
1
0
1
0
1
1
1
0
1
0 







   
1
0
1
1
0
1
1
1
0
0
1 







   
0
1
1
1
0
1
1
1
0
1
1 














1
0
1
1
1
0
]
G
[ 1
   
0
0
0
1
0
1
1
1
0
0
0 







   
1
0
1
1
0
1
1
1
0
1
0 







   
1
1
0
1
0
1
1
1
0
0
1 







   
0
1
1
1
0
1
1
1
0
1
1 














1
1
0
1
0
1
]
G
[ 2

17. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 56
 Code de Hamming groupe
 Correction d'une erreur
1
2
1
2 




 m
k
n m
m

   














...
1
0
1
...
1
1
0
...
:
:
:
...
0
0
...
2
1 n
h
h
h
H avec )
(i
bin
hi 

Mot-erreur :  
....
.... i

 
i
T
j
j
j h
z
H
v
H
z
v
v 







 
 .
.

 L'erreur est à la position dec(hi)
Ex Hamming

18. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 57














7
6
5
4
7
6
3
2
7
5
3
1
i
i
i
c
i
i
i
c
i
i
i
c











1
0
1
0
1
0
1
1
1
0
0
1
1
0
1
1
1
1
0
0
0
H  
7
6
5
4
3
2
1 i
i
i
c
i
c
c
v 
0
. 
T
v
H

Circuit de codage

19. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 58
Circuit de décodage





























7
6
5
4
1
7
6
3
2
2
7
5
3
1
3
i
i
i
c
e
i
i
i
c
e
i
i
i
c
e 2
1
1
2
0
3 2
.
2
.
2
.
pour
1 e
e
e
i
i 





20. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 59
Codes cycliques (Cyclic Redundancy Check / Frame Check Sequence)
• Code cyclique = code linéaire + propriété de permutation
1
1
2
2
1
0 ...
)
( 





 n
n x
a
x
a
x
a
a
x
v
]
....
[ 1
1
0 
 n
a
a
a
v
• Mot-code :
• Bloc de n symboles  polynôme de degré n-1 ! :
• Information : ]
i
....
i
i
[
i 1
k
1
0 
 1
k
1
k
2
2
1
0 x
i
...
x
i
x
i
i
)
x
(
i 






  3
2
x
x
1
1
1
0
1 



21. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 60
• Polynôme générateur : g(x)
- g(x) définit le codeur (n,k)
- g(x) est de degré m=n-k
- Il vérifie :
1
k
n
1
k
n
2
2
1 x
a
...
x
g
x
g
1
)
x
(
g 








)
x
(
p
)
x
(
g
x
1 n



Exemple : code cyclique (n=7, k=4)
)
x
x
1
(
)
x
x
1
(
)
x
1
(
x
1 3
3
2
7









g(x) est de degré 3 soit :
)
x
x
1
(
g(x)
ou
)
x
x
1
(
)
x
(
g 3
3
2







22. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 61
• Matrice génératrice et polynôme générateur














)
x
(
g
.
x
...
)
x
(
g
.
x
)
x
(
g
G
1
k
)
n
,
k
(
Exemple : g(x)=(1+x2+x3)













1
1
0
1
.
.
.
.
1
1
0
1
.
.
.
.
1
1
0
1
.
.
.
.
1
1
0
1
G )
7
,
4
(













1
1
0
1
0
0
0
0
1
1
0
1
0
0
1
1
1
0
0
1
0
1
0
1
0
0
0
1
G )
7
,
4
(
s











1
0
0
1
0
1
1
0
1
0
1
1
1
0
0
0
1
0
1
1
1
H )
7
,
3
(
s

23. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 62
• Codage par multiplication
• Codage par division
• Décodage par division
)
x
(
i
.
x
)
x
(
c
)
x
(
v m

 








)
(
)
(
.
)
(
x
g
x
i
x
Reste
x
c
m
)
x
(
g
)
x
(
i
)
x
(
v 








 

)
(
)
(
)
(
x
g
x
v
Reste
x
z
Si z(x)=0  Transmission OK
Sinon  Détection ou correction
Ex 
     
1
1
0
0
0
1
0
1
0
1
1
1
1
1
0
6
5
)
(
3
2
)
(
3
1
)
(











 x
x
x
x
v
x
x
x
x
i
x
x
x
g et
Systématique !
# convolution discrète !

24. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 63
• Exemple de polynômes générateurs
 ATM
- x8
+ x2
+ x + 1 Cellule ATM
- x10
+ x9
+ x5
+ x4
+ x + 1 Couche AAL type 3/4
 CCITT N°41 X25 (HDLC)
- x16
+ x12
+ x5
+ 1
 IEEE 802 Réseaux locaux
- x32
+ x26
+ x23
+ x22
+ x16
+ x12
+ x10
+ x8
+ x7
+ x5
+ x4
+ x2
+ 1

25. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 64
• Code BCH (Bose-Chaudhuri - Hocquenghem)
 Correction de e erreurs



r
i
i x
m
x
g
1
)
(
)
(
1
2
3
2
1 ,....,
, 


 e
r 





 Exemple
n=15 et e=3
 )
1
)(
1
)(
1
(
)
( 2
4
3
2
4
x
x
x
x
x
x
x
x
x
g 








 m=10

26. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 65
• Code Golay
 Correction de e erreurs parfait
 Nb correcteurs = Nb mots-erreur
e Nombre d'erreurs à corriger = 2m
-1

g(x) polynôme minimal de degré m
 Exemple
n=23 et e=3
 m=11 , k=12
11
10
6
5
4
2
1
)
( x
x
x
x
x
x
x
g 








27. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 66
 Les symboles d'information sont traités en flux continu
 Contrainte : m = nb de blocs contrôlés par un bloc donné
 Rque :Blocs de n0 symboles, mais dont les m0 contrôleurs ne
dépendent pas que des k0 symboles d'information !
 Longueur de contrainte : n=m.n0
Codes convolutifs
• Généralités
 Taux d'émission :
0
0
n
k
R 

28. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 67
• Codes convolutifs systématiques
 
1
2
2
1
1 .....
....... j
jY
X
Y
X
Y
X
V 
 .
...... 0
1 k
j
j
j X
X
X 
 .
...... 0
1 m
j
j
j Y
Y
Y  Contrôle
Information
avec
 Mot-code :
• Codes convolutifs non systématiques
 Contrôle et information sont mélangés
 Mot-code :  
.....
.......
2
1 j
U
U
U
V 

29. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 68
n
n
n
n
n x
R
x
R
x
R
x
R
y .
.
.
. 1
1
2
2
3
3
4 


 


• Exemple : m=4, k0=1, m0=1, n0=2
 R=[1011]

30. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 69
• Représentation des codes convolutifs
- Par le codeur
- Par une matrice de transfert
- Un diagramme d'état
- Un treillis  chemin  décodage par chemin le + probable
X1(n)
X2(n)
U1(n)
U2(n)
U3(n)














0
5
0
0
0
1
0
1
1
G 













2
3
0
1
0
1
1
0
2
G 













4
2
0
0
1
0
1
0
3
G







4
2
0
2
3
5
G

31. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 70
 Exemple : n0=2, R=0.5 , m=3
2
)
2
(
2
1
)
1
(








n
n
n
n
n
n
n
x
x
U
x
x
x
U

32. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 71
 Recherche d'erreur à la fréquence N
Dmin = 2e+1

33. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 72
 Stratégie de recherche de Dmin
 Exemple pour N=3
10 01 10  ?
3
1









i
i
d
Min
11 01 10
• Décodage : algorithme de Viterbi

34. Dpt. Télécommunications, Services & Usages Théorie de l ’information H. Benoit-Cattin 73
• Conclusion sur le codage de canal
 Indispensable
 Théories mathématiques complexes des solutions concrètes
 Recherche de codeurs conjoint source / canal
- Reed-Salomon (1984) : BCH Qaire  DVB(204,188,8)
- Turbo-Codes (1993) : Code convolutif V+H
- complexité --
- robustesse ++
- flexibilité ++