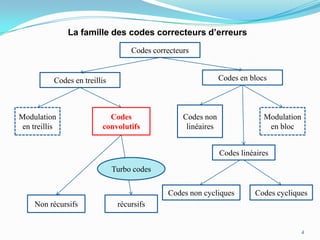
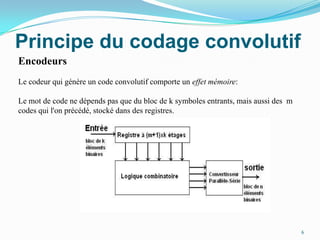
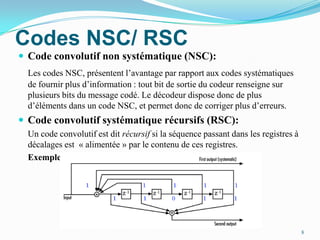
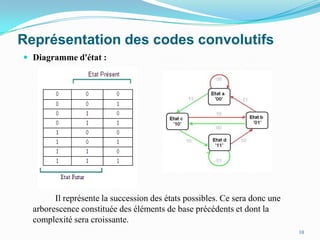
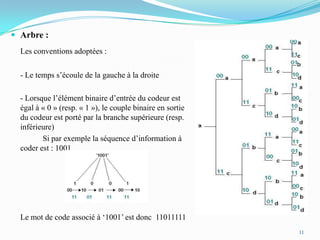
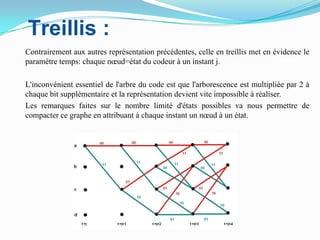
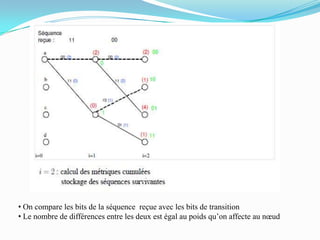
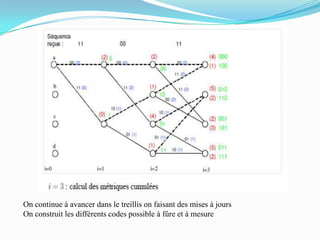
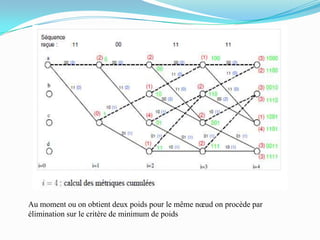
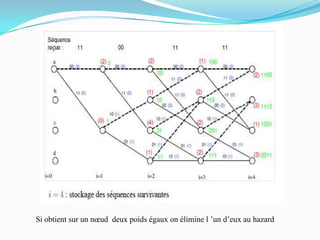
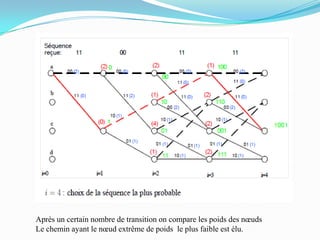
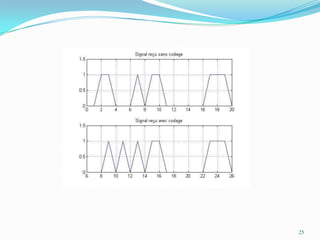
Ce document traite des codes convolutifs dans la théorie de l'information, expliquant leur fonctionnement, leurs propriétés et leurs applications dans les communications modernes. Les codes convolutifs, inventés par Peter Elias en 1954, sont présentés comme des codes correcteurs d'erreurs flexibles et efficaces, largement utilisés dans les systèmes de communication. Il aborde également les algorithmes de décodage, notamment l'algorithme de Viterbi, et donne des exemples d'applications pratiques dans les technologies de télécommunication.

1. 2ème année Génie Des Systèmes De Télécommunications et RéseauxThéorie de l’informationLES CODES CONVOLUTIFSRéalisé par:Proposé par :Assia MOUNIR Mr. LYHYAOUI Anas BENNANI Anouar LOUKILI Ali Broma SIDIBEAnnée scolaire 2008-2009

2. PLANIntroduction Codes convolutifs Généralités Encodeurs Codes NSC/ RSC Diagramme d'états Arbre Treillis Algorithme de décodage: ViterbiMatlabConvenc poly2trellisvitdecExemples & Applications2

3. INTRODUCTIONThéorie de l’information BruitThéorème de Shannon« Tout canal de transmission admet un paramètre C, appelé capacité du canal, tel que pour tout e > 0 et pour tout R < C, il existe un code de taux R permettant la transmission du message avec un taux d’erreurs binaire de e.» 3

4. 4La famille des codes correcteurs d’erreursCodes correcteursCodes en blocsCodes en treillisCodes non linéairesModulation en treillisCodes convolutifsModulation en blocCodes linéairesTurbo codesCodes non cycliquesCodes cycliquesNon récursifsrécursifs

5. Codes convolutifsGénéralités Le principe des codes convolutifs, inventés par ''Peter Elias'' en 1954, est de considérer des séquences semi-infinies a0a1a2… de symboles qui passent à travers une succession de registres à décalage, dont le nombre est appelé mémoire du code, et de générer des séquences semi-infinies. Les codes convolutifs constituent une classe extrêmement flexible et efficace de codes correcteurs d'erreurs. Ce sont les codes les plus utilisés dans les communications fixes et mobiles.5

6. Principe du codage convolutifEncodeurs Le codeur qui génère un code convolutif comporte un effet mémoire:Le mot de code ne dépends pas que du bloc de k symboles entrants, mais aussi des m codes qui l'on précédé, stocké dans des registres.6

7. PropriétésLe rendement du code est: R=k/nLa quantité (m+1).k s'appelle longueur de contrainte du code.LinéaritéStationnarité7

8. Codes NSC/ RSCCode convolutif non systématique (NSC):Les codes NSC, présentent l’avantage par rapport aux codes systématiques de fournir plus d’information : tout bit de sortie du codeur renseigne sur plusieurs bits du message codé. Le décodeur dispose donc de plus d’éléments dans un code NSC, et permet donc de corriger plus d’erreurs.Code convolutif systématique récursifs (RSC): Un code convolutif est dit récursif si la séquence passant dans les registres à décalages est « alimentée » par le contenu de ces registres. Exemple:8

9. ExempleSoit lecodeur convolutif non systématique (k=1, n=2, m=2)Transformée en D9

10. Représentation des codes convolutifsDiagramme d'état : Il représente la succession des états possibles. Ce sera donc une arborescence constituée des éléments de base précédents et dont la complexité sera croissante.10

11. Arbre :Les conventions adoptées : - Le temps s’écoule de la gauche à la droite - Lorsque l’élément binaire d’entrée du codeur est égal à « 0 » (resp. « 1 »), le couple binaire en sortie du codeur est porté par la branche supérieure (resp. inférieure) Si par exemple la séquence d’information à coder est : 1001 Le mot de code associé à ‘1001’ est donc 1101111111

12. Treillis : Contrairement aux autres représentation précédentes, celle en treillis met en évidence le paramètre temps: chaque nœud=état du codeur à un instant j. L'inconvénient essentiel de l'arbre du code est que l'arborescence est multipliée par 2 à chaque bit supplémentaire et la représentation devient vite impossible à réaliser. Les remarques faites sur le nombre limité d'états possibles va nous permettre de compacter ce graphe en attribuant à chaque instant un nœud à un état.

13. Treillis : Un chemin complet commence à l’état S(0,0) et se termine à S(o,L). Un mot de code convolutif n’a pas de longueur fixe, cependant pour des contraintes pratiques la plupart des applications imposent une longueur max du mot . A cet effet, on ajoute m bits (dits bits de queue) nuls, on force ainsi le treillis à revenir à l’état S(0,L).

14. Treillis : Dans ce cas , les codes convolutifs avec terminaison sont vus comme des codes en bloc de rendement: La réduction du taux de codage:ε diminue fortement pour des L>>m

15. Décodage des Codes Convolutifs La contrainte principale du décodage convolutif réside dans le fait que le mot de code est très long, ce qui a tendance à compliquer le circuit décodeur. Les algorithmes de décodage les plus répandus sont : Décodage séquentiel : introduit par WONZENCRAFT(1961) amélioré par FANO(1963) et ZIGANGOROV(1968)Décodage par Seuil : introduit par MASSEY (1963)basé sur la longueur de contrainte du bloc en cours de décodage plutôt que sur l’utilisation de toute la séquence reçue, ce qui conduit à des performances de décodage inférieures aux autres méthodes.Décodage VITERBI : basé sur le principe de max de vraisemblance ( Max Likelihood) Méthode optimale pour le décodage des codes convolutifs.Performances dépendantes de la qualité du canal.Complexité croit exponentiellement avec (m+1)k (contrainte de code)

16. Algorithme de Viterbi : L’algorithme de Viterbi entre dans le cadre du décodage à maximum de vraisemblance des codes convolutifs. Le décodage à maximum de vraisemblance correspond à chercher dans le treillis du code C le chemin le plus proche (le plus vraisemblable) de la séquence reçue.A chaque instant, deux branches appartenant à deux chemins différents, convergent vers chaque nœud. De ces deux chemins, l’un est plus vraisemblable, c’est-à-dire se trouve à une distance plus petite de la séquence reçue, que l’autre chemin. Les distances étant additives, il est possible de ne conserver en chaque nœud que le chemin le plus vraisemblable, appelé survivant. Si deux chemins sont aussi vraisemblables, un seul chemin est arbitrairement conservé.

17. Algorithme de Viterbi: ExempleSoit le treillis élémentaire d'un code convolutif :On considère la séquence d’information suivante : 1001La séquence codée est donc : 11 10 11 11Une erreur survient dans la transmission du troisième bit.La séquence reçue est donc : 11 00 11 11

18. Algorithme de Viterbi: Exemple On décode la séquence reçue en utilisant l’algorithme de Viterbi :

19. On compare les bits de la séquence reçue avec les bits de transition

20. Le nombre de différences entre les deux est égal au poids qu’on affecte au nœudOn continue à avancer dans le treillis on faisant des mises à jours On construit les différents codes possible à fûreet à mesure

21. Au moment ou on obtient deux poids pour le même nœud on procède par élimination sur le critère de minimum de poids

22. Si obtient sur un nœud deux poids égaux on élimine l ’un d’eux au hazard

23. Après un certain nombre de transition on compare les poids des nœuds Le chemin ayant le nœud extrême de poids le plus faible est élu.

24. Partie MatlabConvenc Poly2trellisVitdec24

25. 25

26. 26

27. 27

28. 28

29. 29

30. 30

31. 31

32. 32

33. Exemples et applicationsSatellites de communicationsSatellites militairesSonde spatiale ( voyager)TélémétrieRéseaux sans fils LAN/WANles standards de téléphonie mobile de 2G (GSM) & 3G (UMTS)33

34. 34Exemples :La norme GSM (Global System for Mobile Communications) incorpore un code de longueur de contrainte Kc = 6 et de rendement 1/2.

35. La norme USDC utilise un code avec Kc = 6 et un rendement 1/2.