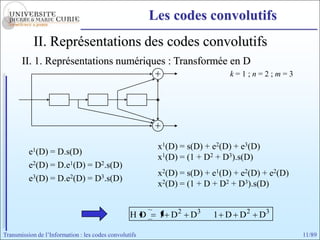
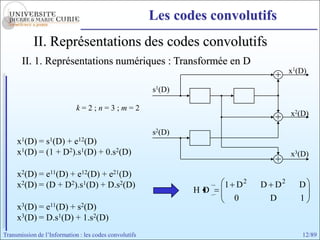
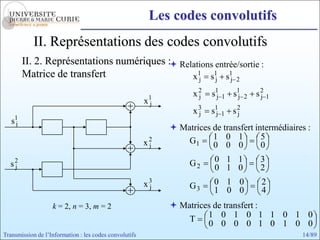
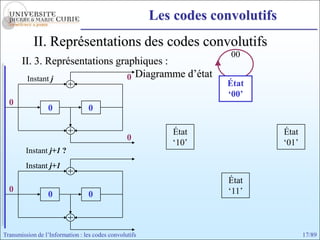
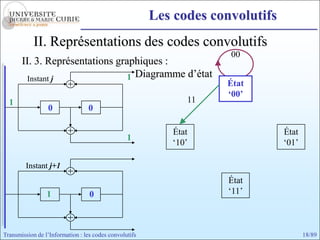
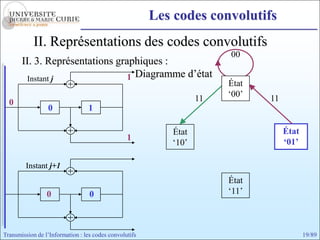
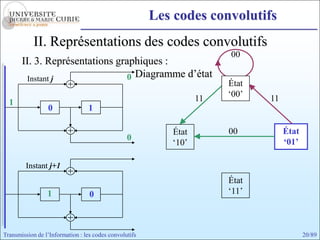
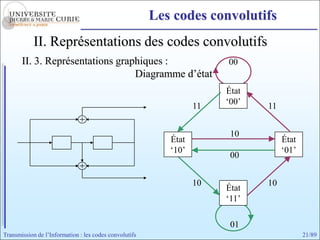
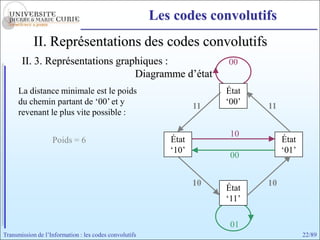
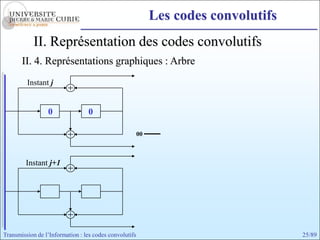
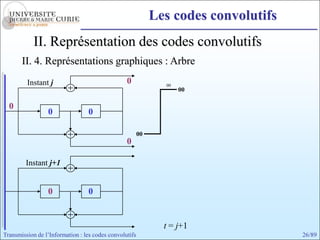
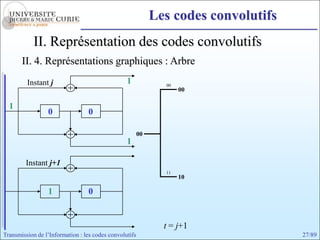
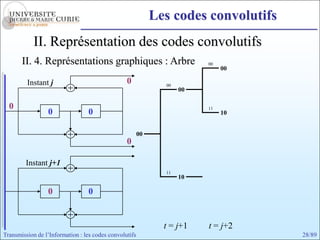
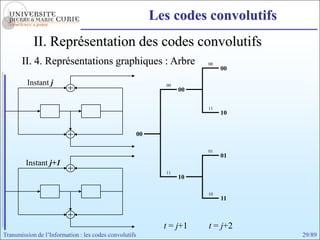
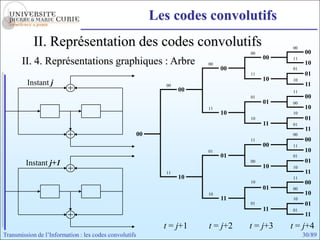
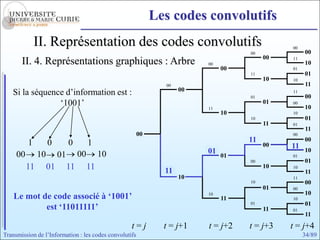
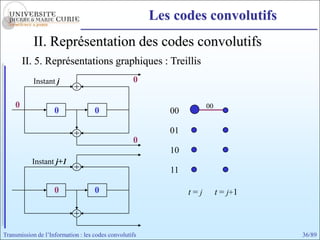
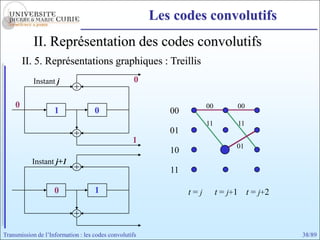
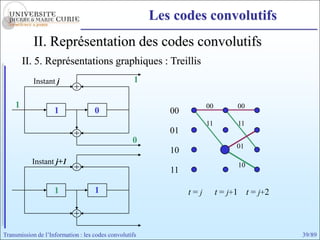
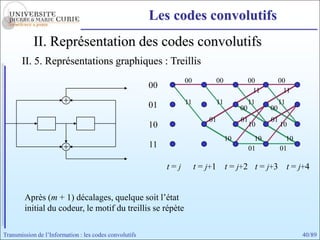
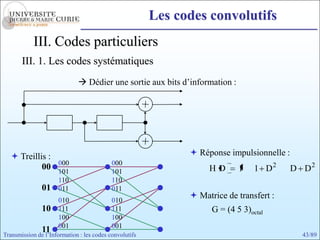
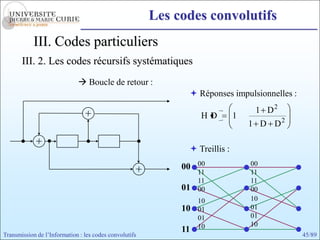
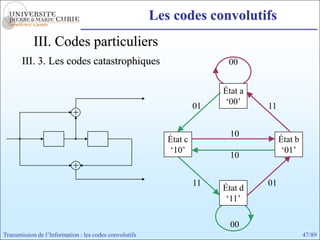
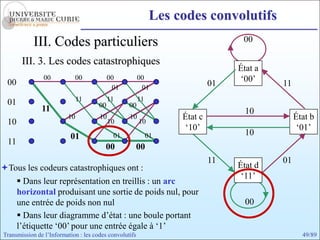
Les codes convolutifs sont des codes correcteurs d'erreur efficaces utilisés dans les communications. Ils reposent sur un principe d'encodage qui utilise des registres de mémoire pour traiter des séquences infinies de symboles. Le document explore les principes de codage, les propriétés des codes, et leurs représentations à travers des diagrammes d'état et des arbres.