La modulation des signaux est essentielle pour transmettre des informations à travers différents supports, en utilisant des techniques telles que la transmission en bande de base et la modulation. Ce document aborde les concepts de bande passante, de spectre, et différents types de modulation (amplitude, fréquence, phase) pour optimiser la transmission des signaux. Il explique également les implications énergétiques et spectrales des différents procédés de modulation sur la qualité de transmission.

![La modulation des signaux vient du besoin de transmettre un signal physique,
support d’une information, entre deux points distants.
Considérons un signal à transmettre s(t), de spectre S(f ).
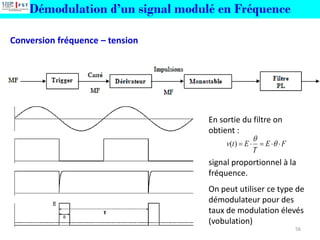
S(f) est la zone de fréquence que le signal occupe, Cette zone appelée largeur
de bande spectrale.
Pour tout signal réel s(t), on a un spectre borné pour lequel on peut définir
une fréquence minimale fm et une fréquence maximale fM telles que S(f)=0
pour toute fréquence en dehors de [fm ,fM].
Exemples :
• signal de parole « téléphonie » : fm = 300 Hz et fM = 3,4 kHz
• signal sonore « haute fidélité » : fm = 20 Hz et fM = 16 kHz
Spectre d’un signal et bande passante d’un support
2
Introduction
Rappels Théoriques](https://image.slidesharecdn.com/modulationanalogique-sahel-221112172757-f1061daa/85/Modulation-Analogique-2-320.jpg)
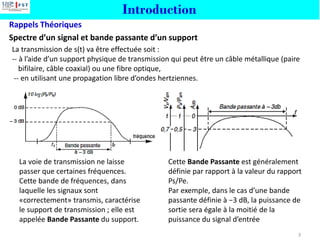


![Nécessité d’une modulation
Introduction
6
Comment transmettre une information si(t) d’un point E (émetteur) vers un
point R (récepteur) ?
si(t) peut être une information issue d’un capteur (microphone, résultat d’une
mesure …) ou un signal traité (résultat d’un calcul, données informatiques …).
Cette information peut aussi être définie dans le domaine spectral, par Si(f).
On suppose que le spectre est compris dans la bande [fL, fH ] ; .](https://image.slidesharecdn.com/modulationanalogique-sahel-221112172757-f1061daa/85/Modulation-Analogique-6-320.jpg)
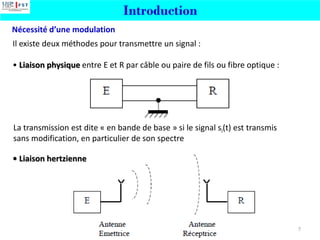



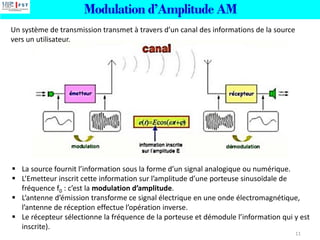









![Modulation d’Amplitude AM
Procédé de modulation, Emetteur
Multiplieurs analogiques à base
d’amplificateurs différentiels
associé à un additionneur:
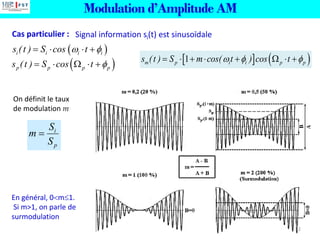
Si l’information est sinusoïdale. E0 permet de régler le taux de modulation m. Pour une
modulation DSBSC, il suffit de faire E0 = 0.
Modulation à multiplication de signaux
Exemple :
25
Elle effectue directement le produit du signal porteur par [1+ms(t)]. Ce multiplieur peut
être représenté par un amplificateur linéaire dont le gain est le signal modulant.](https://image.slidesharecdn.com/modulationanalogique-sahel-221112172757-f1061daa/85/Modulation-Analogique-25-320.jpg)