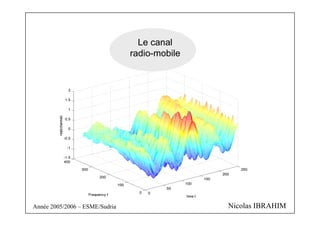
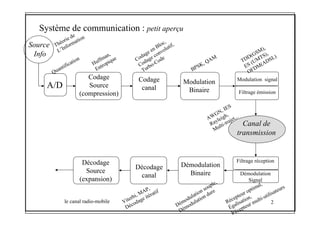
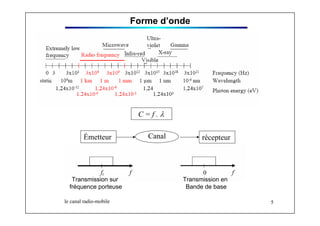
Le document traite du canal radio-mobile, abordant des concepts tels que la modulation, le codage, et les modèles de propagation à long, moyen et court termes. Il décrit également les effets d'évanouissement, les caractéristiques du canal et la modélisation statistique des multipath. Les différentes méthodes de traitement du signal pour optimiser la transmission dans des environnements variés sont également abordées.
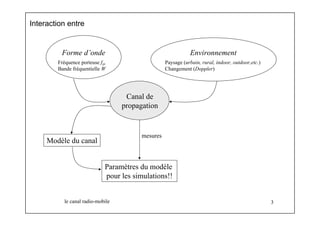


![Modèle de propagation à grande échelle
( ) [dB] 0
⎞
⎛
⎞
⎛
n f
L d
10 , log 10 log 10 α γ + + ⎟ ⎟⎠
= m b f h h
0
10
0
⎜ ⎜⎝
+ ⎟ ⎟⎠
⎜ ⎜⎝
f
d
Le modèle est valable pour une gamme donnée de
distances d , γ
fréquences f , n
hauteur des antennes hm, hb
modèles théoriques Modèles empiriques :
Okumara-Hata, Walfish-Ikegami,
Edwards et Durkin, Carey,
Blonquist et Label, Lee,
Breton et Walfish,
Alsebrook et Parsons,
etc. et etc.
le canal radio-mobile 9](https://image.slidesharecdn.com/nibcours5canalradio-141125011816-conversion-gate02/85/Nib-cours5-canalradio-9-320.jpg)
![Modèle de propagation à moyenne échelle : effet de masque
m±σ
L [dB]
Atténuation en loi log-normale :
10log10(d)
( )
⎞
⎟ ⎟⎠
⎛ −
P g g m
⎜ ⎜⎝
exp
( ) 1
= − 2
2
2 2
πσ σ
2
Suivant les environnements, l’écart type peut varier entre 2 et 12 dB
le canal radio-mobile 10](https://image.slidesharecdn.com/nibcours5canalradio-141125011816-conversion-gate02/85/Nib-cours5-canalradio-10-320.jpg)

![Modélisation temporelle de l’évanouissement
Modèle de Rician, Rayleigh (différence par rapport à la domination du trajet direct)
L’atténuation autour du récepteur est modélisé par :
L(t) = α (t) exp( jφ (t))
φ(t) : variable aléatoire uniformément répartie dans [-π, + π]
α(t) : variable de Rayleigh (variable de Chi centrée du deuxième ordre)
2 2
t x t y t
( ) ( ) ( )
, circulaire si
2
x t N
( ) ~ (0, σ
)
x
( ) ~ (0, )
α
Pr( ) exp
σ σ
⎛
2
α
le canal radio-mobile 12
où
2 y
σ
α
=
⎪⎩
⎪⎨ ⎧
= +
x
y
y t N
⎞
⎟ ⎟⎠
⎜ ⎜⎝
= − 2
2 2
σ
σ
α](https://image.slidesharecdn.com/nibcours5canalradio-141125011816-conversion-gate02/85/Nib-cours5-canalradio-12-320.jpg)
![α(t) : variable de Rice (variable de Chi non-centrée du deuxième ordre)
( )
⎞
⎟ ⎟⎠
⎛
α s I s
⎜ ⎜⎝
⎞
⎟⎠
+ ⎛
2
α
Pr( ) exp
α
α
= − 2 0 2
⎜⎝
2 2
σ
σ
σ
2 2
t x t y t
( ) ( ) ( )
σ
x x , circulaire si ,
s m m
2
x t N m
( ) ~ ( , )
( ) ~ ( , )
x x y
Pr( ) 2
m α
m m
Ω
⎞
⎛
⎛
m
le canal radio-mobile 13
où
2 2 2
2 y
y y
y t N m
= = +
⎪⎩
⎪⎨ ⎧
= +
σ σ
σ
α
α(t) : variable de Nakagami m-distribué
2
[ 2 ] 2
[( 2 )2 ]
2
2 1
E
E ; ,
exp
( )
−Ω
Ω = = =
⎟ ⎟⎠
⎜ ⎜⎝
Ω
− ⎟⎠⎞
⎜⎝
Γ Ω
=
Σ
−
R
R R x m
i
m
α α](https://image.slidesharecdn.com/nibcours5canalradio-141125011816-conversion-gate02/85/Nib-cours5-canalradio-13-320.jpg)



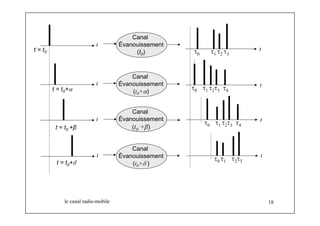
![Modèle du Canal multi-trajet
Le canal est caractérisé par deux profiles :
Profile des retards { τn }
Profile de puissance moyenne associée à chaque retard { Pn }
Pn = E[ (rn)² ]
Autour de la fréquence porteuse, le modèle du canal s’écrit :
L
1
c τ t α π c τ n 2 n t e δ t τ t P n = E[( α
n (t))] Σ−
i f t
( ; ) = ( ) − 2 ( ) ( −
( ))
=
0
n
n
τ est relatif au répétition de l’expérience
t est relatif au déroulement de l’expérience Canal stationnaire : c(t)
c(τ, t) est une variable gaussienne complexe selon la variable τ
le canal radio-mobile 19](https://image.slidesharecdn.com/nibcours5canalradio-141125011816-conversion-gate02/85/Nib-cours5-canalradio-19-320.jpg)
![1- Temps
Pour deux retards différents, quelle est la ressemblance des réponses ?
( , ; ) E[ *
( 1 ; ) ( 2
; )] 1 2 t c t c t t c Φ τ τ Δ = τ τ + Δ
Généralement, pour les canaux radio-mobile,
( ) ( ) ( ) 1 2 1 1 2 Φ τ ,τ ;Δt = Φ τ ;Δt δ τ −τ c c
Donc, indépendance entre les réponses sur les différents trajets
(τ ) (τ ) c c Φ ;0 = Φ
Puissance moyenne du canal
le canal radio-mobile 21
τ](https://image.slidesharecdn.com/nibcours5canalradio-141125011816-conversion-gate02/85/Nib-cours5-canalradio-21-320.jpg)
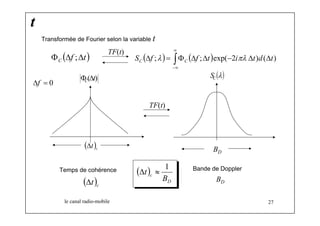
![2- Fréquence
∞
C( f , t) = ∫c(τ , t) exp ( − 2
iπ f τ )dτ
−∞
le canal radio-mobile 23
τ
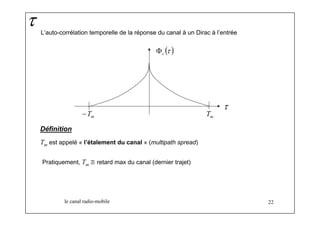
L’auto-corrélation fréquentielle de la réponse du canal à un Dirac à l’entrée
( , ; ) E[ *
( 1 ; ) ( 2
; )] 1 2 f f t C f t C f t t C Φ Δ = + Δ
c(τ ,t) C( f ,t) TF
( f f t) ( f t) C C Φ , ;Δ = Φ Δ ;Δ 1 2 ( t) c Φ , ;Δ 1 2 τ τ TF
Ne dépend que de la différence entre les fréquences !!!](https://image.slidesharecdn.com/nibcours5canalradio-141125011816-conversion-gate02/85/Nib-cours5-canalradio-23-320.jpg)





![Performance sur canal à évanouissment
Modèle du signal reçu
r(t) =α (t)s(t) + n(t)
Probabilité d’erreur est donnée par
⎞
⎟ ⎟
⎠
⎛
Pr( ) 2
⎜ ⎜
γ
Q b
⎝
=
0
N
γ
b
∞
=
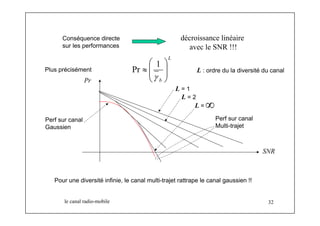
Pr Pr( γ b ) p ( γ b ) dγ b Pr ≈ 1 =
Es
E [( α
2 )]
le canal radio-mobile 31
avec
( (t)s(t))2 E .( (t))2 b s γ = α = α
Les performances instantanées sont dominées par la puissance instantanée du trajet
∫
0
0
γ N
b](https://image.slidesharecdn.com/nibcours5canalradio-141125011816-conversion-gate02/85/Nib-cours5-canalradio-31-320.jpg)