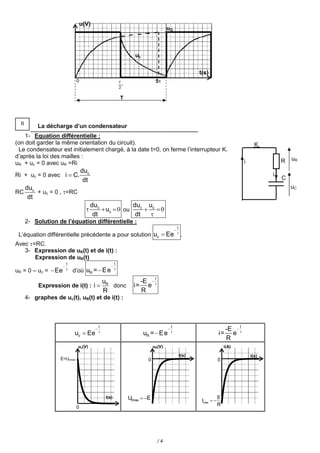
Ce document présente le comportement d'un dipôle RC en réponse à un échelon de tension, comprenant des équations différentielles pour modéliser la charge et la décharge d'un condensateur. Il détaille la solution de ces équations, les relations entre courant, tension et constante de temps, ainsi que des graphiques illustrant ces concepts. Enfin, il aborde la durée de charge d'un condensateur et les régimes transitoire et permanent associés.

1. LYCEE ZAHROUNI-TUNIS-
SCIENCES PHYSIQUES
4ème MATH
Cours
Boussada .A 2 www.physiqueweb2.c4.fr
LE DIPÔLE RC
I
Réponse d’un dipôle RC à un échelon de tension
1 Dipôle RC C
R
Le dipôle RC est constitué d’un condensateur associé en série avec un
résistor (conducteur ohmique).
2 Echelon de tension u(V)
U est une tension appliquée aux bornes du dipôle RC, à t=0 s on E
ferme le circuit. Si :
Pour t<0 ; u =0
Pour t  0 ; u = E.
On dit alors qu’on applique un échelon de tension au dipôle RC. t(s)
3 Relation entre i(t) et uc(t)
dq
En courant variable : i(t) = .
dt
C
+q -q
i dq d(Cuc ) du
i avec q  C.uc donc i   C. c
dt dt dt
uC à retenir
4 Equation différentielle K
(on doit représenter les flèches des tensions avant d’établir l’équation
différentielle). i R uR
Le condensateur est initialement déchargé, à la date t=0, on ferme
uG
l’interrupteur K. E i
d’après la loi des mailles : C
uR + uc + uG= 0 avec uR =Ri et uG= - E uC
duc
Ri + uc - E = 0 or i  C.
dt
duc
RC  uc  E , on pose =RC
dt
duc duc uc E
  uc  E ou  
dt dt  
5 Solution de l’équation différentielle
a- Solution de l’équation différentielle :
L’équation différentielle précédente a pour solution uC = A + Be-t.
Avec A ; B et  sont des constantes positives. Déterminons A ; B et  :
1ère étape : Le condensateur est initialement vide uC(0) = 0.
A + Be0 =0  A + B =0 donc B= - A. D’ou uC = A – Ae-t.
ème
2 étape : lorsque t  + ∞ ; le condensateur est complètement chargé : uC (∞) = E.
A – Ae-∞ = E or e-∞ =0.
A – 0 = E d’où A=E et B= - E.
Donc uC = E – Ee-t.
uC = E( 1 – e-t).
/1

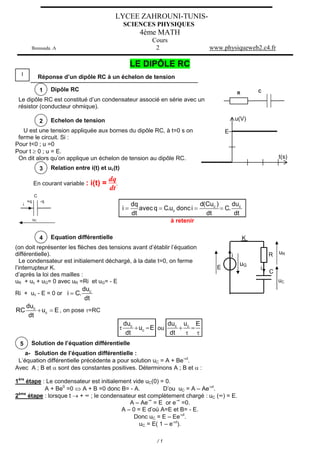
2. duc
3ème étape : Cette solution vérifie l’équation différentielle RC  uc  E
dt
Donc : RCE(0 – (-)e-t) + E( 1 – e-t) = E
RCEe-t + E -E e-t = E  RCEe-t -E e-t = 0  Ee-t( RC - 1 ) = 0.
Or Ee-t >0 d’où RC - 1 = 0  RC = 1   =  = .
RC 
uC = E(1- e-t/ ).
6 Expression de uR(t) et de i(t)
t t t
  
Expression de uR(t) ; uR = E – uc = E - E(1  e  ) = E –E + E e 
d’où uR =E e 
Expression de i(t)
t
u E 
i  R donc i= e
R R
7 Graphes de uc(t), uR(t) et de i(t)
t t t
  E 
uc  E(1  e  ) uR =E e 
i= e
R
uR(V) i(A)
uc
E
E E=URmax Imax 
R
E t(s) t(s)
0 0 0
X
t(s) 0 + t(s) 0 + t(s) 0 +
E E
uc(V) 0 E u (V) E 0 i(A) 0
R R R
8 La constante de temps  C
a- Définition : I
La constante de temps  est une grandeur caractéristique du dipôle RC, elle nous renseigne sur la rapidité
avec laquelle s’effectue la charge ou laC décharge d’un condensateur.
b- Unité de  : E
uR V
R donc R est en S
  R C a v e c { i A d ' où  est en
V A.s
.  s
(seconde) donc  est un temps.
C
q D en
o r q  I.t d o n c C e s t
A.s A V
uc V
c- Détermination de  :
E
S
 Par calcul : Ayant les valeurs de R(en Ω) et de C(en F), on peut calculer directement (en s) ;  = RC .
Y
 Graphiquement : 1ère méthode (utilisation de la tangente à l’origine) : on peut montrer que  est
N
l’abscisse du point d’intersection de la tangente à la courbe de uc (t)[de même pour uR(t), i(t) et q(t)] à la
date t=0 avec l’asymptote (lorsque t+).
T
H u (V) R
TangenteE E=u Rmax
u (V
)
c
S Tangente
E=Uc E
max Asymptote
Point Asymptote
Ex t(s)
d’intersection 0
er 
cic
e1 Point
t(s)
 E d’intersection
0
X
E /2

3. o 2ème méthode (lecture graphique) :
er
1 cas : à partir du graphe de uc(t)
Pour t=, quelle est la valeur de uc ?

uc()  E(1  e )  E(1  e 1)

0, 63.E car e 1 0, 37
Exemple :
On a E= 4 V d’où 0,63.4 =2,52 V donc l’abscisse du point d’ordonnée 2,52 V est égale à 
uc(V)
4
2,52
t(s)
0
2ème cas : à partir du graphe de uR(t) 
uR(V)
Pour t=, quelle est la valeur de uR ?
 4
uR()  E.e   E.e 1 0, 37.E
Exemple :
On a E= 4 V d’où 0,37.4 =1,48 V donc l’abscisse du point
d’ordonnée 1,48 V est égale à . 1,48
9 Durée de charge d’un condensateur t(s)
0 
On peut considérer qu’un condensateur est complètement chargé lorsque
sa tension uc = 0,99E ce qui donne une durée de charge t  5 = 5RC
Le temps de charge augmente avec R et avec C.
Pour t < 5, on a le régime transitoire.
Pour t  5, on a le régime permanent.
Remarque :
 la réponse d’un dipôle RC à un échelon de tension est la charge progressive du condensateur : c’est un
phénomène transitoire.
 Charge d’un condensateur par une tension créneaux.
K Voie YA
i R
G.B.F Voie YB
A
i C uG
uc
B
T
Pour 5 < , pendant une demi-période la tension uc peut atteindre sa valeur finale donc on observe les
2
courbes suivantes (les deux voies ont la même sensibilité verticale) :
u(V)
Um
uc
uG
t(s)
T
5 2
T
T
Pour 5 > , pendant une demi-période la tension uc
2
ne peut pas atteindre sa valeur finale donc on observe les courbes suivantes :
/3

4. u(V)
uG
uc
t(s)
0 T 5
2
T
II
La décharge d’un condensateur
1- Equation différentielle :
(on doit garder la même orientation du circuit). K
Le condensateur est initialement chargé, à la date t=0, on ferme l’interrupteur K.
d’après la loi des mailles : uR
uR + uc = 0 avec uR =Ri i R
duc
Ri + uc = 0 avec i  C. i
dt C
duc uC
RC + uc = 0 , =RC
dt
duc duc uc
  uc  0 ou  0
dt dt 
2- Solution de l’équation différentielle :
t

L’équation différentielle précédente a pour solution uc  Ee 
.
Avec =RC.
3- Expression de uR(t) et de i(t) :
Expression de uR(t)
t t
 
uR = 0 – uc =  Ee 
d’où uR =  E e 
t
uR -E  
Expression de i(t) : i  donc i= e
R R
4- graphes de uc(t), uR(t) et de i(t) :
t t t
  -E  
uc  Ee 
uR =  E e 
i= e
R
uc(V) uR(V) i(A)
t(s) t(s)
E=Ucmax 0 0
t(s) URmax  E E
Imax  
R
0
/4