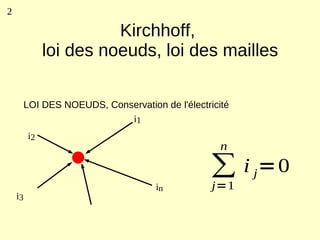
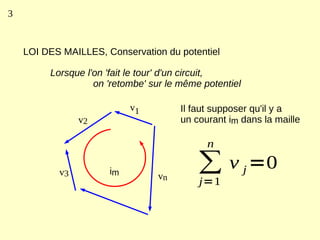
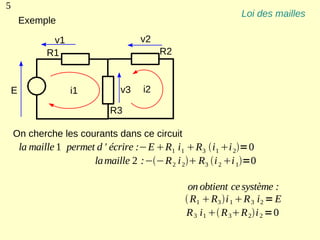
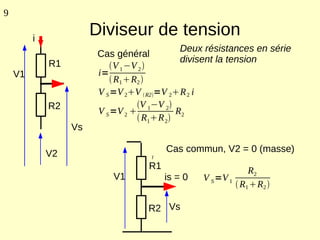
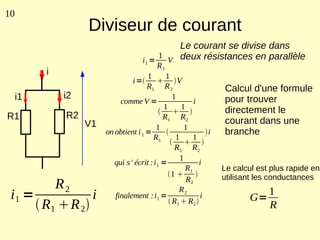
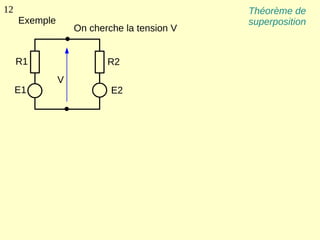
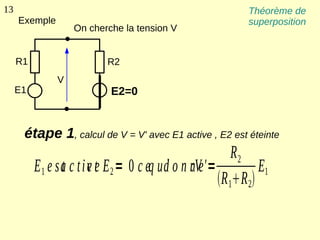
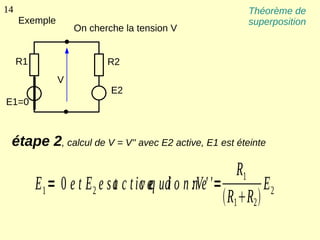
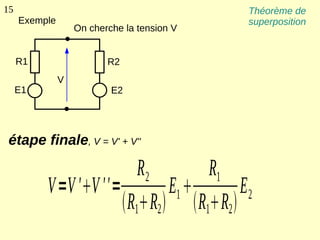
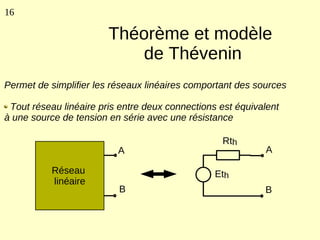
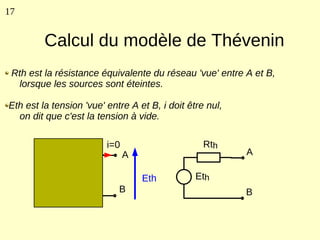
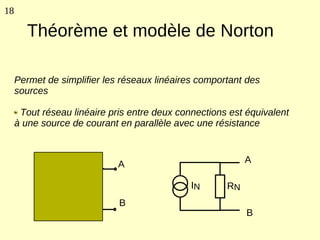
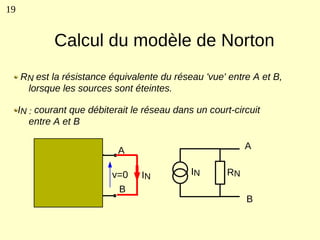
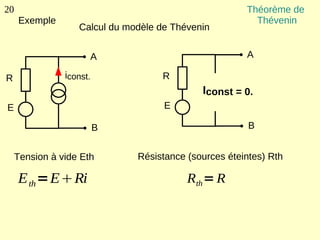
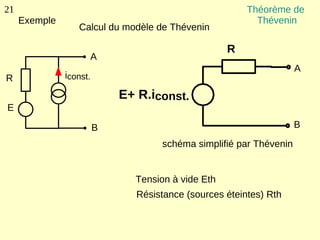
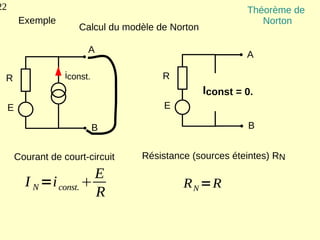
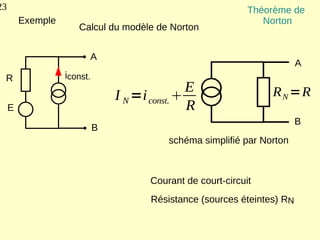
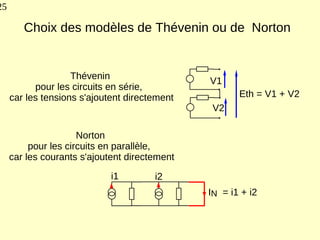
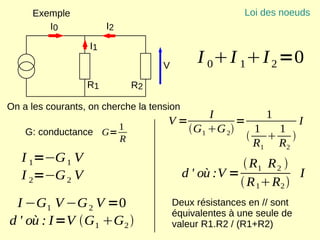
Ce document explique les lois de Kirchhoff concernant les circuits électriques linéaires, incluant la loi des nœuds et la loi des mailles, qui permettent d'analyser et de modéliser divers circuits. Il aborde également les théorèmes et méthodes de réduction, tels que les théorèmes de Thévenin et de Norton, et des techniques pratiques comme le diviseur de tension et le diviseur de courant. Enfin, il présente des cas particuliers permettant de simplifier les calculs dans des configurations courantes de circuits.

1. 1
Lois des circuits
électriques
linéaires
Dominique BERGOGNE

2. 2
Kirchhoff,
loi des noeuds, loi des mailles
LOI DES NOEUDS, Conservation de l'électricité
i1
i2
n
∑ i j=0
in j=1
i3

3. 3
LOI DES MAILLES, Conservation du potentiel
Lorsque l'on 'fait le tour' d'un circuit,
on 'retombe' sur le même potentiel
v1 Il faut supposer qu'il y a
v2 un courant im dans la maille
n
v3 im vn
∑ v j =0
j=1

4. 4
Les lois de Kirchhoff permettent de
mettre en équations tous les réseaux
électriques linéaires.
C'est la méthode utilisée dans les
simulateurs de circuits électriques.

5. 5
Loi des mailles
Exemple
v1 v2
R1 R2
E i1 v3 i2
R3
On cherche les courants dans ce circuit
la maille 1 permet d ' écrire :−E R1 i 1 R3 i 1 i 2=0
la maille 2 :−−R 2 i 2 R3 i 2 i 1=0
on obtient ce système :
 R1 R3 i 1 R 3 i 2 = E
R 3 i 1  R 3R 2i 2 =0

6. 6
Cas remarquables,
formules rapides
On retrouve souvent les même types de circuits.
On peut tirer une formule ou un théorème pour certains cas
particuliers afin ne plus avoir à utiliser Kirchhoff.
association série
association parallèle
diviseur de tension
diviseur de courant
théorème de superposition
théorème et modèle de Thévenin
théorème et modèle de Norton

7. 7
Association série
Plusieurs résistances branchées en série
sont équivalentes à une seule résistance
V1 V2 Vn
i V 1 =R1 i V 2 =R 2 i V n =Rn i
R1 R2 Rn V = R1 R2 ⋯ Rn i
R V V =Réquivalente i
2 n
Le courant est unique Réquivalente = ∑ R j
j=1
n
∑ V j =V
j=1

8. 8
Association parallèle
Plusieurs résistances branchées en parallèle
sont équivalentes à une seule résistance
1 1 1
i 1= V i 2= V i n= V
i R1 R2 Rn
1 1 1
i1 i2 in i=  ⋯ V
R 1 R2 Rn
v
1
i= V
R équivalente
R1 R2 Rn 1
Réquivalente = n
La tension est unique 1
∑ R 
n j =1 j
∑ i j=i
j=1

9. 9
i
Diviseur de tension
Deux résistances en série
Cas général
R1 divisent la tension
V 1 −V 2 
V1 i=
 R1 R2 
V S =V 2V  R2=V 2R 2 i
R2 V 1−V 2
V S =V 2  R2
 R1R 2
Vs
V2 Cas commun, V2 = 0 (masse)
I
R1 R2
V1 is = 0 V S =V 1
 R1 R2 
R2 Vs

10. 10
Diviseur de courant
Le courant se divise dans
V deux résistances en parallèle
1
i1 =
R1
i 1 1
i =  V
R1 R 2 Calcul d'une formule
i1 i2 1 pour trouver
comme V = i
1 1 directement le
  
R1 R2 R1 R2
V1 courant dans une
1 1
on obtient i 1 =  i branche
R1 1 1
  
R 1 R2
1
qui s ' écrit : i 1 = i
R1 Le calcul est plus rapide en
1   utilisant les conductances
R2
R2 R2 1
i1 = i finalement : i 1 = i G=
 R1 R 2  R1  R2 
R

11. 11
Théorème de superposition
Permet de simplifier les calculs en superposant séparément
les actions de chaque source actives dans un réseau linéaire.
Pour étudier l'action d'une source seule, on 'éteint' les autres sources.
Une source de courant éteinte est un circuit ouvert
Une source de tension éteinte est un court-circuit
Les sources liées ne peuvent pas être éteintes
La solution cherchée (un courant ou une tension)
est la somme des solutions trouvées avec chaque source seule

12. 12 Théorème de
Exemple superposition
On cherche la tension V
R1 R2
V
E1 E2

13. 13 Théorème de
Exemple superposition
On cherche la tension V
R1 R2
V
E1 E2=0
étape 1, calcul de V = V' avec E1 active , E2 est éteinte
R2
E 1 e s a c t i v te E 2 = 0 c eq u di o n n e '=
t e :V E1
R 1R 2

14. 14 Théorème de
Exemple superposition
On cherche la tension V
R1 R2
V
E2
E1=0
étape 2, calcul de V = V'' avec E2 active, E1 est éteinte
R1
E 1 = 0 e t E 2 e s a c t i cv eq u di o n :Ve' '=
t e n E2
R1 R2 

15. 15 Théorème de
Exemple superposition
On cherche la tension V
R1 R2
V
E1 E2
étape finale, V = V' + V''
R2 R1
V =V 'V ''= E1  E2
R1R2  R1R2 

16. 16
Théorème et modèle
de Thévenin
Permet de simplifier les réseaux linéaires comportant des sources
Tout réseau linéaire pris entre deux connections est équivalent
à une source de tension en série avec une résistance
Rth
A A
Réseau Eth
linéaire
B B

17. 17
Calcul du modèle de Thévenin
Rth est la résistance équivalente du réseau 'vue' entre A et B,
lorsque les sources sont éteintes.
Eth est la tension 'vue' entre A et B, i doit être nul,
on dit que c'est la tension à vide.
i=0 Rth
A A
Eth Eth
B B

18. 18
Théorème et modèle de Norton
Permet de simplifier les réseaux linéaires comportant des
sources
Tout réseau linéaire pris entre deux connections est équivalent
à une source de courant en parallèle avec une résistance
A A
IN RN
B
B

19. 19
Calcul du modèle de Norton
RN est la résistance équivalente du réseau 'vue' entre A et B,
lorsque les sources sont éteintes.
IN : courant que débiterait le réseau dans un court-circuit
entre A et B
A A
v=0 IN IN RN
B
B

20. 20 Théorème de
Exemple Thévenin
Calcul du modèle de Thévenin
A A
R iconst. R
Iconst = 0.
E E
B B
Tension à vide Eth Résistance (sources éteintes) Rth
E th =ERi Rth = R

21. 21 Théorème de
Exemple Thévenin
Calcul du modèle de Thévenin
R
A
A
R iconst.
E+ R.iconst.
E
B B
schéma simplifié par Thévenin
Tension à vide Eth
Résistance (sources éteintes) Rth

22. 22 Théorème de
Exemple Norton
Calcul du modèle de Norton
A
A
R iconst. R
Iconst = 0.
E E
B B
Courant de court-circuit Résistance (sources éteintes) RN
E
I N =i const.  R N =R
R

23. 23 Théorème de
Exemple Norton
Calcul du modèle de Norton
A
A
R iconst.
E R N =R
I N =i const. 
E R
B
B
schéma simplifié par Norton
Courant de court-circuit
Résistance (sources éteintes) RN

24. 24
Equivalence des modèles de Thévenin et Norton
Les modèles de Thévenin et Norton sont équivalents
car ils sont la représentation du même réseau linéaire.
Il est possible de passer de l'un à l'autre facilement.
R N =Rth Thévenin
pour les circuits en série,
car les tensions s'ajoutent directement
E th=R N I N
Norton
E th pour les circuits en parallèle,
I N= car les courants s'ajoutent directement
R th

25. 25
Choix des modèles de Thévenin ou de Norton
Thévenin
V1
pour les circuits en série,
car les tensions s'ajoutent directement Eth = V1 + V2
V2
Norton
pour les circuits en parallèle,
car les courants s'ajoutent directement
i1 i2
IN = i1 + i2

26. Exemple Loi des noeuds
I0 I2
I1
V
I 0I 1I 2 =0
R1 R2
On a les courants, on cherche la tension
I 1
1
V= = I
G: conductance G= G1 G 2 1 1
R   
R 1 R2
I 1=−G 1 V  R1 R 2 
I 2=−G 2 V d ' où :V = I
 R 1R2 
I −G1 V −G 2 V =0 Deux résistances en // sont
équivalentes à une seule de
d ' où : I =V G1 G2  valeur R1.R2 / (R1+R2)