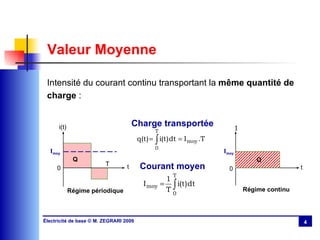
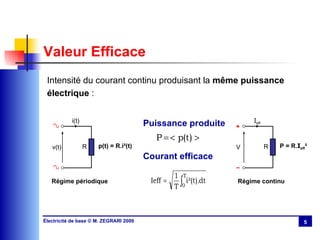
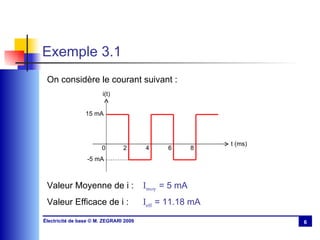
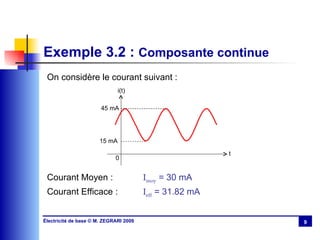
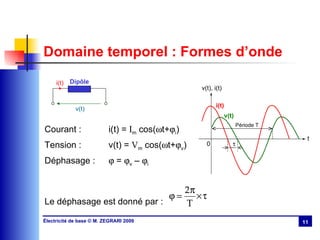
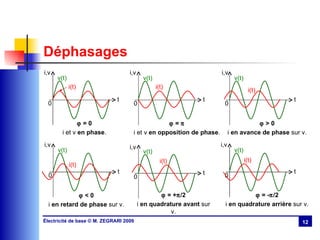
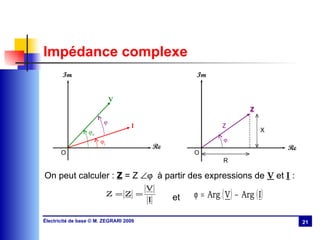
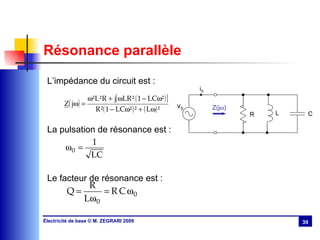
Le chapitre 3 aborde le régime sinusoïdal permanent, présentant les caractéristiques des signaux périodiques et les circuits en régime sinusoïdal. Il traite des concepts tels que la valeur moyenne, la valeur efficace, l'impédance, la puissance active et réactive, ainsi que des lois d'association des circuits. Le chapitre explique également la résonance dans les circuits RLC et discute de l'importance du facteur de puissance et de sa compensation.

1. Chapitre 3 REGIME SINUSOIDAL PERMANENT Prof. Mourad ZEGRARI

2. Plan Caractéristiques des signaux périodiques Grandeur sinusoïdale Étude des circuits en RSP Puissances en RSP Circuits résonnants

3. Grandeur périodique -alternative Grandeur périodique i(t+T) = i(t) : reproduction au bout de la période T. Grandeur alternative Alternativement positive et négative au bout de T. Symétrique É galité des aires positifs et négatifs.

4. Valeur Moyenne Intensité du courant continu transportant la même quantité de charge : Charge transportée Courant moyen I t 0 Q I moy Régime continu 0 T t i(t) I moy Régime périodique Q

5. Valeur Efficace Intensité du courant continu produisant la même puissance électrique : Puissance produite Courant efficace R p(t) = R.i²(t) Régime périodique v(t) i(t) Régime continu + – R P = R. I eff ² V I eff

6. Exemple 3.1 On considère le courant suivant : Valeur Moyenne de i : I moy = 5 mA Valeur Efficace de i : I eff = 11.18 mA i(t) 15 mA -5 mA 0 2 4 6 8 t (ms)

7. Grandeur sinusoïdale Courant sinusoïdal : i(t) = I m cos(  t+  ) i(t) : intensité instantanée (A) I m : valeur maximale (A)  t+  : phase instantanée (rad)  : phase à l’origine, t=0 (rad)  = 2  f : pulsation (rad/s) f : fréquence (Hz) T = 1/ f : période (s) I m cos φ i(t) I m t 0 T - I m

8. Caractéristiques Valeur moyenne : Valeur efficace : Signal à composante continue : i’(t) = I 0 + I m cos(  t+  ) Valeur moyenne : Valeur efficace :

9. Exemple 3.2 : Composante continue On considère le courant suivant : Courant Moyen : I moy = 30 mA Courant Efficace : I eff = 31.82 mA i(t) 45 mA 15 mA t 0

10. Représentations en RSP Domaine temporel On représente la forme d’onde de la grandeur en fonction du temps : i(t) , v(t) ,.. Domaine de Fresnel On représente géométriquement les grandeurs par des vecteurs tournants : I , V ,.. Domaine du phaseur On représente symboliquement les grandeurs dans le plan complexe : I , V ,..

11. Domaine temporel : Formes d’onde Courant : i(t) = I m cos(  t+  i ) Tension : v(t) = V m cos(  t+  v ) Déphasage :  =  v –  i Le déphasage est donné par : 0 t  v(t) i(t) v(t), i(t) Période T i(t) v(t) Dipôle

12. Déphasages v(t) t 0 i(t)  = 0 i et v en phase . i,v v(t) t 0 i(t)  =  i et v en opposition de phase . i,v v(t) t 0 i(t)  > 0 i en avance de phase sur v. i,v v(t) t 0 i(t)  = -  /2 i en quadrature arrière sur v. i,v v(t) t 0 i(t)  < 0 i en retard de phase sur v. i,v v(t) t 0 i(t)  = +  /2 i en quadrature avant sur v. i,v

13. Domaine géométrique : Plan de Fresnel On représente les vecteurs à l’instant t = 0 : i(t) = I m cos(  t+  i ) : Vecteur I de module I m et déphasé de  i . v(t) = V m cos(  t+  v ) : Vecteur V de module V m et déphasé de  v . L’écart angulaire  =  v -  i traduit le déphasage de i par rapport à v. X φ v O ω + I m V m φ φ i Y I V

14. Domaine du Phaseur : Plan complexe On représente les vecteurs I et V dans le plan complexe : i(t) = I m cos(  t+  i ) = R e { I m e j(  t+  i) } : I = I m cos  i + j I m sin  i v(t) = V m cos(  t+  v ) = R e { V m e j(  t+  v) } : V = V m cos  v + j V m sin  v En pratique, on note : I = I m  i et V = V m  v Re φ v O I m V m φ φ i Im I V

15. Impédances et admittances Impédance : Z Quotient des valeurs efficaces : Z = V eff / I eff Impédance complexe : Z Quotient des valeurs complexes : Z = V / I Admittance complexe : Y L’inverse de l’impédance complexe : Y = Z -1 = I / V Lois d’association : Association en série : Z eq = ∑ Z i Association en parallèle : Y eq = ∑ Y i

16. Dipôles Linéaires : Résistance Domaine du temps : Domaine du phaseur : V = R I Domaine de Fresnel : les vecteurs I et V sont en phase. R i(t) v(t) I V

17. Dipôles Linéaires : Inductance Domaine du temps : Domaine du phaseur : V = jL  I Domaine de Fresnel : le vecteur I est en quadrature arrière sur le vecteur V . L i(t) v(t) I V

18. Dipôles Linéaires : Condensateur Domaine du temps : Domaine du phaseur : V = -( j/C  ) I Domaine de Fresnel : le vecteur I est en quadrature avant sur le vecteur V . I V C i(t) v(t)

19. Éléments Linéaires : Résumé Élément Impédance Admittance Résistance R Z R = R Y R = G = 1/R Inductance L Z L = jL  Y L = -j/L  Condensateur C Z C = -j/C  Y C = jC 

20. Impédance : Expression générale En général, une impédance s’écrit : Z = R + jX L’impédance Z s’écrit : Z = Z  et Résistance Réactance i(t) v(t) Dipôle Electrique D R i(t) v(t) jX Z = R + jX

21. Impédance complexe On peut calculer : Z = Z  à partir des expressions de V et I : et Re O I V Im φ φ i φ v Re O Z Im φ R X Z

22. Admittance complexe En Régime Sinusoïdal Permanent : Y = G + jB On peut établir l’équivalence suivante : et R i(t) v(t) jB Conductance Susceptance i(t) v(t) Dipôle Electrique D Y = G + jB

23. Analyse des circuits en RSP Lois de Kirchhoff Loi des nœuds : ∑I k = 0 Loi des mailles : ∑V k = 0 Méthode des courants fictifs Théorèmes généraux Théorème de Millman Théorème de superposition Théorème de Thévenin Théorème de Norton

24. Étapes de synthèse Transformer le circuit dans le domaine des phaseurs Remplacer chaque élément par son impédance en RSP. 2. Établir les phaseurs des courants et des tensions Représenter chaque grandeur par son phaseur. 3. Établir les équations d’équilibre Appliquer les lois et les théorèmes de base de l’électrocinétique 4. Résoudre les équations des phaseurs Déterminer le module et la phase des différentes grandeurs mises en jeu.

25. Exemple d’étude Phaseur du courant : Z eq = 20 + j10.48 = 22.58  27.7°  ; I S = 0.44  -27.7° A Phaseurs des tensions : V R = 8.8  -27.7° V ; V L = 22.12  62.3° V ; V C = 17.51  -62.3° V R = 20  i s C = 10 µF L = 20 mH v S v R v C v S (t) = 10 cos(800  t) On considère le circuit suivant : v L

26. Puissance instantanée Un dipôle parcouru par i et soumis à v tel que : i(t) = I m cos(  t+  i ) ; v(t) = V m cos(  t+  v ) La puissance instantanée p(t) est le produit des valeurs instantanées de i et de v : p(t) = v(t) . i(t) En considérant les valeurs efficaces I et V on obtient : Composante continue Puissance Moyenne Composante alternative Puissance Fluctuante

27. Puissance instantanée t v(t) i(t) t t p(t) Puissance moyenne VIcosφ VI

28. Puissance active C’est la valeur moyenne de la puissance instantanée p(t) : P = < p(t) > En posant :  =  v -  i on peut écrire : P = V I cos  La puissance P correspond à des effets observables physiquement. La nature de fonctionnement est donné selon le signe de P : P > 0 : le dipôle consomme de la puissance : Récepteur P < 0 : le dipôle fournit de la puissance : Générateur

29. Puissance réactive Elle est donnée par la relation : Q = V I sin  La puissance réactive correspond à des effets non observables physiquement. Elle traduit les échanges d’énergie entre la source et une inductance ou un condensateur.

30. Puissance apparente C’est le produit des valeurs efficaces du courant et de la tension : S = V I La puissance apparente correspond à la puissance maximale que peut dissiper le dipôle. Il s'agit surtout d'une puissance de dimensionnement pour les transformateurs et les lignes d'alimentation.

31. Puissance complexe Si on représente les puissances dans le plan complexe : On en déduit : On montre que : Re O Im φ P Puissance active Puissance réactive Q Puissance complexe S Puissance apparente S

32. Répartition des puissances On considère une impédance : Z = R + jX La puissance dissipée dans l’impédance Z est : Puissance active P = R I ² Puissance réactive Q = X I ² i(t) v(t) Z = R + jX D R i(t) v(t) jX

33. Puissances en RSP : Résumé Puissance complexe : Puissance apparente : S = │ S │ = VI (VA) Puissance active : P = Re { S } = VI cos  (W) Puissance réactive : Q = Im { S } = VI sin  (VAR) Facteur de puissance : Fp = P/S = cos 

34. Facteur de puissance Pour une puissance active donnée, plus le facteur de puissance est faible, plus la puissance apparente est grande et plus le courant sur la ligne est élevé. Ceci entraîne des équipements d'alimentation (ligne de transport, transformateurs) de grande capacité ainsi que des pertes Joule sur la ligne de transport trop élevées.

35. Compensation du facteur de puissance Afin d'augmenter le facteur de puissance de l'installation, on connecte en parallèle un condensateur de valeur appropriée. Avant : P , Q , S ;  Après : P , Q’ , S’ ;  ’ Le condensateur fournit la puissance réactive nécessaire pour compenser celle absorbée par la charge inductive. P Q S Q C S’ Q’

36. Résonance dans les circuits RLC On considère un circuit RLC alimenté par une source de tension sinusoïdale v S de pulsation  variable : L’impédance du circuit : Z = Z(j  ) Le circuit est en résonance à la pulsation  0 si l’impédance Z (j  ) est purement résistive à cette fréquence : Z (j  0 ) = R 0 = réelle i S v S Circuit RLC A B Z(j  )

37. Facteur de qualité Ce facteur est définit comme : Où : W m : valeur maximale de l’énergie emmagasinée. W d : énergie dissipée pendant une période : Q L : puissance réactive totale dans les inductances. Q C : puissance réactive totale dans les condensateurs. P : puissance active totale dissipée dans les résistances.

38. Résonance série L’impédance du circuit est : La pulsation de résonance est : Le facteur de résonance est : C i S R L v S Z(j  )

39. Résonance parallèle L’impédance du circuit est : La pulsation de résonance est : Le facteur de résonance est : C i S R L v S Z(j  )

40. Résonance série-parallèle L’impédance du circuit est : La pulsation de résonance est : Le facteur de résonance est : C i S R L v S Z(j  )

41. Résonance parallèle-série L’impédance du circuit est : La pulsation de résonance est : Le facteur de résonance est : C i S R L v S Z(j  )