Norton thevenin

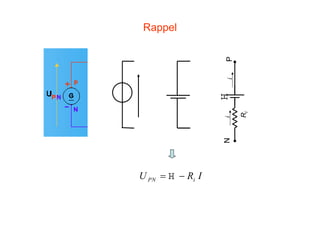
1. Rappel
PN iU R I= −E
iPN
Ri
Ei

2. Rappel

3. Loi de Kirchhoff
Déterminer le courant I

4. Cherchons la valeur des courants I1, I2 et I3 dans le circuit
Loi de Kirchhoff

5. Appliquer les lois de Kirchhoff au circuit suivant afin de déterminer les
valeurs et les sens corrects des courants I1, I2 et I3. Préciser ensuite la
fonction des trois accumulateurs et, enfin, calculer le potentiel du
point B si l’on relie le point A à la masse (VA = 0).
Les sens des courants sont
choisis arbitrairement. on
constate que seul le
sens du courant I3 doit être
modifié. Les trois
accumulateurs sont des
générateurs
Loi de Kirchhoff

6. Comporte 6 mailles, 3 noeuds et 5 branches. Il nous faudra cinq équations
indépendantes pour trouver les 5 courants.
Loi de Kirchhoff

7. Théorème de Thévenin
Théorème de Thévenin
Un réseau compris entre deux noeuds A et B est équivalent à un
générateur indépendant de tension parfait ETh en série avec le dipôle
composé ZTh.
A
B
?
A
B
UAB
ZTh
E T h
ETh représente la tension UAB
lorsque AB est ouvert
ZTh est l'impédance entre les
points A et B lorsqu’on supprime
les générateurs

8. Schéma équivalent de Thevenin du dipôle AB
1
1 3
E
i
R R
=
+
Exprimer le courant i2 en fonction des
éléments du montage (Thévenin)
E1 = 10 V, E2 = 5 V, R1 = 15 W,
R2 = 10 W et R3 = 5 W
A remplacer par
Générateur de Thevenin
AB ThU E=
On supprime les
générateurs
On détermine la tension
entre A et B: UAB
i On applique la loi des
mailles pour déterminer
le courant
3AB ThU R i E= =

9. Schéma équivalent de Thevenin du dipôle AB
ETh
RTh
On applique la loi des mailles pour
déterminer le courant

10. Dans le circuit représenté ci-dessous, on veut prévoir le courant qui traversera
une résistance R placée entre A et B.
On commence par enlever cette résistance et on calcule la valeur du courant qui
passe dans la maille de manière à pouvoir calculer la tension équivalente de
Thévenin, tension entre les bornes A et B, en l’absence de charge (c’est-à-dire, si
R n’est pas relié)
Résistance équivalente de
Thévenin; correspond à la résistance
mesurée entre les bornes A et B
lorsqu’on annule la tension des deux
sources.
Schéma équivalent de Thévenin du dipôle AB

11. Théorème de Norton
Un réseau compris entre deux noeuds A et B est équivalent à une source
indépendante de courant réelle IN en parallèle avec une impédance ZN.
IN est le courant électromoteur, c'est à dire lorsque AB est en court-circuit.
ZN est obtenue lorsqu’on supprime tous les générateurs (comme pour
Thévenin).
A
B
?
A
B
UAB
ZNIN

12. Schéma équivalent de Norton du dipôle AB
Déterminer le dipôle équivalent de
Norton du dipôle AB ci-contre
On court-circuite AB: courant équivalent
de Norton (Icc)
Les lois des mailles et des nœuds

13. Schéma équivalent de Norton du dipôle AB
Les sources E1 et E2 sont remplacées
par leur « résistance interne » (Pour une
source de tension, c’est une résistance
nulle)
la résistance équivalente

14. Équivalent de Thévenin-Norton.
Tout dipôle linéaire peut être modélisé par un dipôle équivalent de
Thévenin ou par un dipôle équivalent de Norton
ETH est la tension vue entre les deux bornes du dipôle est à vide.
(réseau linéaire non relié à un autre réseau électrique).
Icc est le courant de court-circuit entre les deux bornes de ce dipôle.
Req est la résistance vue entre les deux bornes du dipôle lorsque
toutes les sources indépendantes sont remplacées par leur
résistance interne.
Les modèles de Thévenin et de Norton sont reliés par la relation

15. Équivalent de Thévenin-Norton.
Nous avons déterminé un dipôle
équivalent de Norton Icc, Req au dipôle
constitué de E1, R1 et E2, R2. (Sans
toucher à la branche qui contient i3).
Le dipôle équivalent de Norton Icc, Req peut
maintenant être transformé en son
équivalent de Thévenin.

16. En déduire la valeur de i3
Appliquer la loi des mailles

17. Exercice 2
Quel est dipôle équivalent entre les bornes A et B
Le dipôle AB se comporte comme un
simple conducteur

18. Exercice 3
On considère le réseau représenté par
le schéma ci-contre: En utilisant le
théorème de Thévenin, calculer le
courant dans la résistance R.
On donne:
E1 = 3 V. R1 = R2 = R3 = 2 .
E 2 = 1 V. R = 5 .
E3 = 2 V.

19. Exercice 3
Ces deux dipôles sont en parallèle . On
peut les remplacer par un dipôle
équivalent de Norton

20. Exercice 3
équivalents de Thévenin.
Ensuite, on appliquera la loi des mailles
pour calculer le courant I.

21. Exercice 4
Par application du théorème de THEVENIN, calculer le modèle équivalent entre
les bornes A et B à l’ensemble du réseau dont le schéma encadré est ci-contre.
(Déterminer le schéma équivalent au dipôle à gauche de A1B1. Faire de même
avec A2B2. Puis faire de même avec AB).

22. Exercice 4
Une source de tension en parallèle avec un autre dipôle se
comporte vis à vis du reste du montage comme la source de
tension seule.

23. Exercice 4
Par la formule du pont diviseur de tension
La résistance « vue » entre les bornes A2/B2
est constituée de deux résistances en parallèles

24. Exercice 4

25. Exercice 4
Loi des mailles :
Formule du pont diviseur de tension
La résistance « vue » entre les bornes A/B est constituée de deux
résistances en parallèle

26. Exercice 5
Calculer le courant dans la résistance R1 en fonction de E, I, R et R1.
Chercher l’Équivalent Norton

27. Exercice 5
Chercher l’Equivalent Norton

28. Exercice 5
En utilisant la dualité Norton/Thévenin, on en déduit

29. Exercice 5

30. En appliquant la loi des mailles

31. Exercice 6 -THEVENIN - NORTON
En appliquant la transformation THEVENIN - NORTON et une loi des mailles,
calculer le courant I1 en fonction de E, I, R

32. Exercice 6
E1
R1 R2 R3
A
M
E2
Exercice 6: Déterminer l’intensité du
courant I2 qui traverse R2, en utilisant le
théorème de Thévenin.
1 3
e
1 3
R q
R R
R R
=
+
3
1
3 1 1
1 3
AM Th
AM M A
U E
U V V R i
E
R i E R i i
R R
=
= − =
= − ⇒ =
+
1
3
1 3
Th
E
E R
R R
=
+
2 2 2 2
2
2
2
0Th Th
Th
Th
R i E R i E
E E
i
R R
+ − − =
−
=
+
i2

33. Exercice 7
R1 R2
R3
A
M
I1 B
1 2 3
1 2 3
( )
RN
R R R
R R R
+
=
+ +
Exercice 7 : On cherche le dipôle
équivalent Norton entre B et M.
R1 R2
R3
A
M
I1 B
ICCIcc
I1
I2
IN = Icc est obtenu en court-circuitant BM
Loi des mailles
2 1 2 1
1
1 2 1 2
0cc
cc
cc
R I R I R
I I
I I I R R
− + = ⎫
⇒ =⎬
= + +⎭

34. Exercice 8
Exercice 8 : Calculer le dipôle équivalent
Thévenin entre les bornes B et M.
1 2
1 2 2
1 2
2
1 1 2 2 1 1
1 2
( ) 0
T CD D C
T
R R
R U V V R I
R R
R
E R R I E E
R R
= = − =
+
− + = =
+
4
1
3 4
3 4 1
2
1
Th
R
E E
R R
R R R
R
=
⎛ ⎞+
+ + +⎜ ⎟
⎝ ⎠
1 2 3 1 2
4
1 2 1 2 3 4
( )
( )( )
Th
R R R R R
R R
R R R R R R
+ +
=
+ + +
4BM ThU E R I= =
4
1
1 3 4
Th T
T
R
E E
R R R
=
+ +
1 3 4
1
1 3 4
( )T
T
T
R R R
R
R R R
+
=
+ +
1 1 3 4( ) 0T TE R I R R I− − + =

35. Théorème de Millman
Le théorème de Millman, appelé aussi théorème des noeuds, permet de
déterminer le potentiel d'un noeud où aboutissent des branches
composées d'un générateur de tensions.
La démonstration de ce théorème consiste à transformer chaque
branche en source de courant, de courant électromoteur
E 1 E 2 E 3 E n
Z1
Z3 ZnZ2
A
B
V
∑
∑
=
== n
i
i
n
i
ii
Y
Y
V
1
1
E
i
i
Z
Y
1
=
ii
i
i
i Y
Z
I E
E
==
i
i
AB
i
i
I
I
V
Y Y
= =
∑
∑
Z1 Z2
Z
E 1 E 2
I
A
B
1 2
1 2 2 1 1 2
1 2 2 1
1 2
( )
1 1 1AB
Z Z Z Z Z Z
V
Z Z Z Z Z Z
Z Z Z
+ +
+
= =
+ ++ +
E E 0
E E