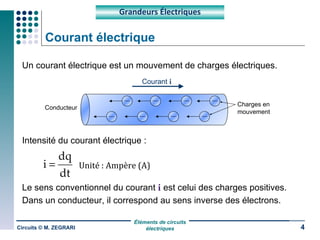
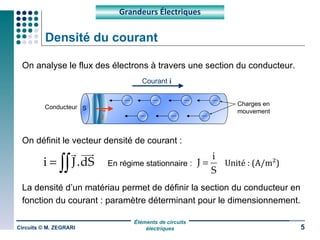
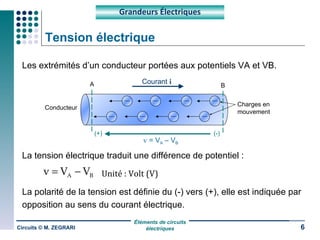
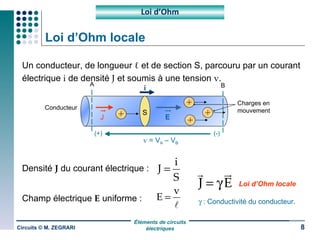
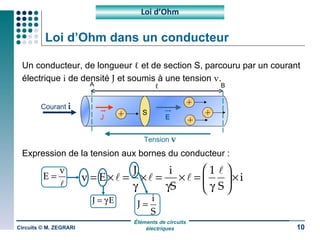
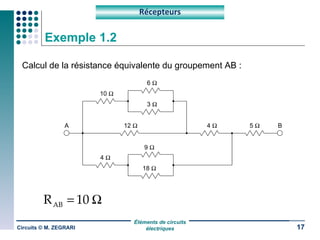
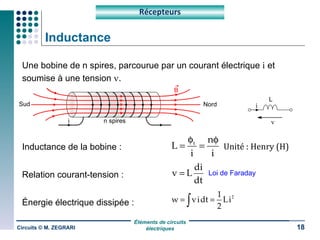
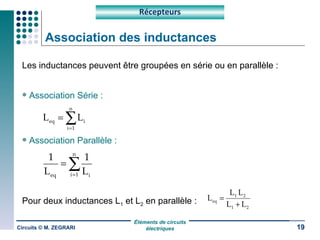
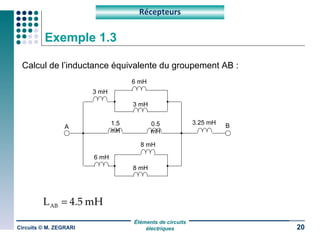
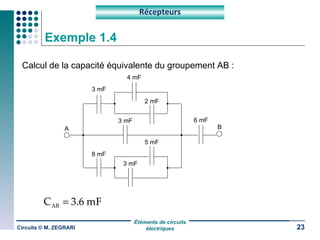
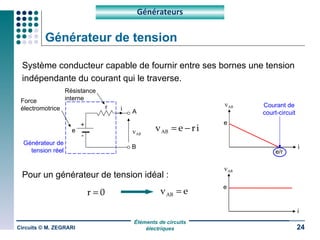
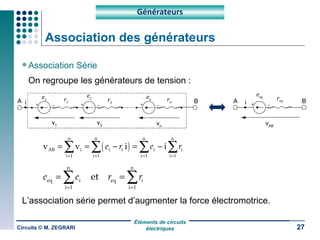
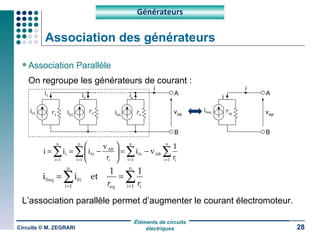
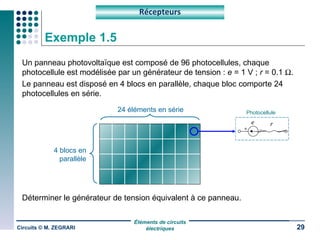
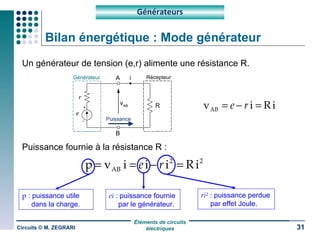
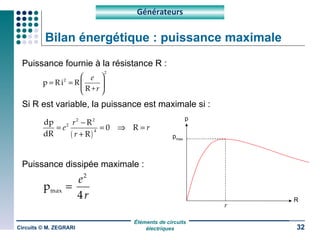
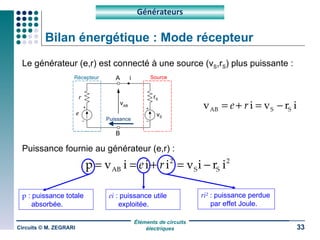
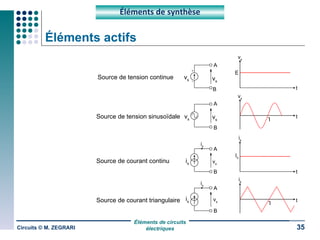
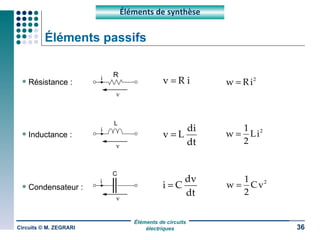
Ce document traite des circuits électriques, en abordant les concepts fondamentaux tels que la loi d'Ohm, les grandeurs électriques, et les classifications des matériaux selon leur conductivité. Il explique également le fonctionnement des composants comme les récepteurs, inductances, condensateurs et générateurs, ainsi que les principes de calcul liés à leur résistance, capacité et puissance. Enfin, il décrit la synthèse des circuits électriques et les étapes de conception d'un système électrique.

1. Cours CIRCUITS ÉLECTRIQUES ÉLÉMENTS DE CIRCUITS ÉLECTRIQUES Prof. Mourad ZEGRARI Chapitre 1

2. Plan Grandeurs électriques Loi d’Ohm Récepteurs de l’énergie électrique Générateurs de l’énergie électrique Éléments de synthèse des circuits électriques Linéarité des circuits électriques Circuits © M. ZEGRARI Éléments de circuits

3. Rupture de l’équilibre Deux conducteurs A et B reliés par u fil conducteur. Un champ électrique est créé à l’intérieur du conducteur : Mouvement des charges mobiles (Force de Coulomb). Création d’un courant électrique, maintenu tant que V A  V B Circuits © M. ZEGRARI Grandeurs Électriques V A V B A B Mouvement des électrons

4. Courant électrique Un courant électrique est un mouvement de charges électriques. Intensité du courant électrique : Le sens conventionnel du courant i est celui des charges positives. Dans un conducteur, il correspond au sens inverse des électrons. Circuits © M. ZEGRARI Grandeurs Électriques Courant i Conducteur Charges en mouvement Unité : Ampère (A)

5. Densité du courant On analyse le flux des électrons à travers une section du conducteur. On définit le vecteur densité de courant : La densité d’un matériau permet de définir la section du conducteur en fonction du courant : paramètre déterminant pour le dimensionnement. Circuits © M. ZEGRARI Grandeurs Électriques Courant i Conducteur Charges en mouvement S J Unité : (A/m²) En régime stationnaire :

6. Tension électrique Les extrémités d’un conducteur portées aux potentiels VA et VB. La tension électrique traduit une différence de potentiel : La polarité de la tension est définie du (-) vers (+), elle est indiquée par opposition au sens du courant électrique. Circuits © M. ZEGRARI Grandeurs Électriques Courant i Conducteur Charges en mouvement A B v = V A – V B (+) (-) Unité : Volt (V)

7. Énergie et puissance électriques Un conducteur parcouru par un courant i et soumis à une tension v . Énergie électrique Puissance électrique Circuits © M. ZEGRARI Grandeurs Électriques Unité : Joule (J) ou (Wh) Unité : Watt (W) p - w Puissance p(t) Énergie w(t) t

8. Loi d’Ohm locale Un conducteur, de longueur ℓ et de section S, parcouru par un courant électrique i de densité J et soumis à une tension v . Densité J du courant électrique : Champ électrique E uniforme : Circuits © M. ZEGRARI Loi d’Ohm i Conducteur Charges en mouvement A B v = V A – V B (+) (-) S E Loi d’Ohm locale  : Conductivité du conducteur. J

9. Classification des matériaux Les matériaux sont classés électriquement suivant leur conductivité : Les conducteurs électriques : matériaux à conductivité élevée, le nombre d’électrons libres est grand et permet la circulation de courants électriques importants. Les isolants électriques : matériaux à faible conductivité, le nombre d’électrons libre est faible et le courant électrique est négligeable. Les semi-conducteurs : leur conductivité est intermédiaire entre celles des conducteurs et des isolants. Le matériau doit être polarisé pour qu’un courant électrique puisse circuler. Les semi-conducteurs sont utilisés dans la fabrication des composants électroniques. Circuits © M. ZEGRARI Loi d’Ohm

10. Loi d’Ohm dans un conducteur Un conducteur, de longueur ℓ et de section S, parcouru par un courant électrique i de densité J et soumis à une tension v . Expression de la tension aux bornes du conducteur : Circuits © M. ZEGRARI Loi d’Ohm Courant i A B Tension v S E ℓ J

11. Résistance d’un conducteur Un conducteur, de longueur ℓ et de section S, parcouru par un courant électrique i de densité J et soumis à une tension v . Tension aux bornes du conducteur : Résistance du conducteur : Conductance d’un conducteur : Circuits © M. ZEGRARI Loi d’Ohm Courant i A B Tension v S ℓ Loi d’Ohm Unité : Ohm (  ) Unité : Siemens (S)

12. Résistivité d’un conducteur La résistance d’un conducteur s’écrit : La résistivité  du conducteur est donnée par : La résistivité dépend également de la température : Circuits © M. ZEGRARI Loi d’Ohm Unité : Ohm-mètre (  .m)  0 : résistivité à la température  = 0 °C.  : coefficient de température du matériau.  : température d’utilisation en °C.

13. Exemple 1.1 L'enroulement d'un transformateur est bobiné avec un fil en cuivre, de résistivité  = 1.7  10 -8  .m et de coefficient de température  = 4  10 -3 . La résistance du fil à 20 °C est de 0,2  . Pendant le fonctionnement normal, cette résistance est portée à 0,25  . Calculer la température de fonctionnement de ce transformateur. Expression de la résistance : Rapport entre les résistances : Température de fonctionnement : Circuits © M. ZEGRARI Loi d’Ohm

14. Effet Joule Lorsqu’un courant électrique circule dans un conducteur, les électrons libres entrent en collision avec les ions fixes du conducteur. Ces chocs répétitifs entraînent une augmentation de la température : effet Joule . Soit un conducteur de résistance R, parcouru par un courant d’intensité i et soumis à une tension v . La puissance dissipée par effet Joule est : L’énergie consommée est entièrement convertie en chaleur. Circuits © M. ZEGRARI Loi d’Ohm

15. Résistance Un conducteur cylindrique, de longueur ℓ et de section S, parcouru par un courant électrique i et soumis à une tension v . Résistance du conducteur : Relation courant-tension : Énergie électrique dissipée : Circuits © M. ZEGRARI Récepteurs Unité : Ohm (  ) Loi d’Ohm i A B v S ℓ v i R

16. Association des résistances Les résistances peuvent être groupées en série ou en parallèle : Association Série : Association Parallèle : Pour deux résistances R 1 et R 2 en parallèle : Circuits © M. ZEGRARI Récepteurs

17. Exemple 1.2 Calcul de la résistance équivalente du groupement AB : Circuits © M. ZEGRARI Récepteurs A B 10  6  3  12  9  4  18  4  5 

18. Inductance Une bobine de n spires, parcourue par un courant électrique i et soumise à une tension v . Inductance de la bobine : Relation courant-tension : Énergie électrique dissipée : Circuits © M. ZEGRARI Récepteurs Nord Sud i n spires B Unité : Henry (H) Loi de Faraday v i L

19. Association des inductances Les inductances peuvent être groupées en série ou en parallèle : Association Série : Association Parallèle : Pour deux inductances L 1 et L 2 en parallèle : Circuits © M. ZEGRARI Récepteurs

20. Exemple 1.3 Calcul de l’inductance équivalente du groupement AB : Circuits © M. ZEGRARI Récepteurs A B 6 mH 3 mH 3 mH 8 mH 6 mH 8 mH 1.5 mH 3.25 mH 0.5 mH

21. Condensateur Un condensateur plan, les armatures sont une surface S et séparées par un diélectrique d’épaisseur e et de permittivité  . Capacité du condensateur : Relation courant-tension : Énergie électrique dissipée : Circuits © M. ZEGRARI Récepteurs Unité : Farad (F) Loi de Gauss Isolant - q +q A B S E e v i C

22. Association des condensateurs Les condensateurs peuvent être groupées en série ou en parallèle : Association Série : Association Parallèle : Pour deux condensateurs C 1 et C 2 en parallèle : Circuits © M. ZEGRARI Récepteurs

23. Exemple 1.4 Calcul de la capacité équivalente du groupement AB : Circuits © M. ZEGRARI Récepteurs A B 4 mF 2 mF 3 mF 5 mF 8 mF 3 mF 3 mF 6 mF

24. Générateur de tension Système conducteur capable de fournir entre ses bornes une tension indépendante du courant qui le traverse. Pour un générateur de tension idéal : Circuits © M. ZEGRARI Générateurs r B v AB i e A Générateur de tension réel + - Force électromotrice Résistance interne v AB i e Courant de court-circuit v AB i e e/r

25. Générateur de courant Système conducteur capable de fournir un courant indépendant de la tension à ses bornes. Pour un générateur de courant idéal : Circuits © M. ZEGRARI Générateurs r 0 B v AB i i 0 A Générateur de courant réel + - Courant électromoteur Résistance interne v AB i r 0 i 0 i 0 v AB i e i 0

26. Équivalence entre les générateurs Deux générateurs sont équivalents s’ils présentent la même caractéristique courant-tension : Circuits © M. ZEGRARI Générateurs r B v AB i e A Générateur de tension + - r 0 B v AB i i 0 A Générateur de courant + - v AB i e e/r v AB i r 0 i 0 i 0

27. Association des générateurs Association Série On regroupe les générateurs de tension : L’association série permet d’augmenter la force électromotrice. Circuits © M. ZEGRARI Générateurs B A v AB e 1 e 2 r 1 r 2 e n r n v 1 v 2 v n A r eq e eq i B i

28. Association des générateurs Association Parallèle On regroupe les générateurs de courant : L’association parallèle permet d’augmenter le courant électromoteur. Circuits © M. ZEGRARI Générateurs B A v AB B i i 01 r 1 i 1 i 02 r 2 i 2 i 0n r n i n i 0eq r eq i A v AB i

29. Exemple 1.5 Un panneau photovoltaïque est composé de 96 photocellules, chaque photocellule est modélisée par un générateur de tension : e = 1 V ; r = 0.1  . Le panneau est disposé en 4 blocs en parallèle, chaque bloc comporte 24 photocellules en série. Déterminer le générateur de tension équivalent à ce panneau. Circuits © M. ZEGRARI Récepteurs 4 blocs en parallèle 24 éléments en série e r Photocellule

30. Exemple 1.5 Générateur de tension équivalent à chaque : Transformation du générateur de chaque bloc en générateur de courant : Générateur de courant équivalent au panneau : Générateur de tension équivalent au panneau : Circuits © M. ZEGRARI Récepteurs

31. Bilan énergétique : Mode générateur Un générateur de tension (e,r) alimente une résistance R. Puissance fournie à la résistance R : Circuits © M. ZEGRARI Générateurs ri² : puissance perdue par effet Joule. A B i v AB Puissance Récepteur R p : puissance utile dans la charge. ei : puissance fournie par le générateur. e r Générateur

32. Bilan énergétique : puissance maximale Puissance fournie à la résistance R : Si R est variable, la puissance est maximale si : Puissance dissipée maximale : Circuits © M. ZEGRARI Générateurs p max p R r

33. Bilan énergétique : Mode récepteur Le générateur (e,r) est connecté à une source (v S ,r S ) plus puissante : Puissance fournie au générateur (e,r) : Circuits © M. ZEGRARI Générateurs ri² : puissance perdue par effet Joule. e A B r i v AB Puissance Source Récepteur p : puissance totale absorbée. ei : puissance utile exploitée. r S v S

34. Synthèse des circuits électriques Un système électrique est un ensemble de composants électriques connectés suivant une certaine configuration afin de réaliser une fonction spécifique. Les étapes de conception d’un système électrique sont : Analyser le comportement du système dans les différentes états. Décomposer le système global en plusieurs entités simples. Représenter chaque entité par une description mathématique. Connecter les différentes entités pour obtenir le modèle du système. Le modèle du système ainsi obtenu est appelé circuit électrique . Circuits © M. ZEGRARI Éléments de synthèse

35. Éléments actifs Circuits © M. ZEGRARI Éléments de synthèse E t v s B A t v s B A T v s Source de tension sinusoïdale Source de tension continue i s t v s B A t v s B A T i s Source de courant triangulaire Source de courant continu i s i s I 0 v s v s v s i s i s

36. Éléments passifs Résistance : Inductance : Condensateur : Circuits © M. ZEGRARI Éléments de synthèse v i R v i L v i C

37. Transformateurs Éléments magnétique à deux paires de bornes : Rapport de transformation : Circuits © M. ZEGRARI Éléments de synthèse Source Charge Circuit magnétique Récepteur à la source. n 1 n 2 i 1 v 1 Primaire Secondaire Générateur à la charge. v 2 i 2 v 2 v 1 i 2 i 1 Symbole du transformateur. m  1 : transformateur élévateur de tension. m  1 : transformateur abaisseur de tension. m = 1 : transformateur d’ isolement .