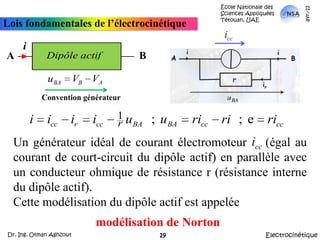
Ce document présente les lois fondamentales de l'électrocinétique, qui étudie le transport des charges électriques dans les circuits conducteurs. Il décrit des concepts clés tels que la circulation du courant électrique, les dipôles, les circuits en série et en parallèle, ainsi que des applications pratiques, incluant des calculs d'intensité et de charge. De plus, il aborde les conventions de signaux et les caractéristiques des dipôles actifs et passifs.

1. Electrocinétique IElectrocinétique IIRégime continuDr. Ing. Otman Aghzout

2. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueIntroductionL’Electrocinétique est la branche de l’´Electromagnétisme qui étudie le transport des charges électriques dans les circuits conducteurs. Elle a envahi tous les secteurs de l’économie et de la vie quotidienne. Il suffit d’imaginer ce qu’il nous arriverait si la terre était privée de tout courant électrique pendant vingt-quatre heures. . .L’énergie électrique est essentiellement obtenue par conversion d’énergie chimique, dans les centrales thermiques – les énergies hydrauliques (barrages) et nucléaires (centrales) restant minoritaires à l’échelle planétaire. l’Electrocinétique est enseignée dans un but pratique. Il ne s’agit pas d’exposer des théories spectaculaires ou de réaliser des prouesses mathématiques, mais de décrire les situations simples et concrètes que rencontre la technologie.ElectrocinétiqueDr. Ing. Otman Aghzout2

3. +-École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueCourant électriqueLe courant électrique est un déplacement de charges électriques dans la matière.Les électrons chargés négativement circulent :de la borne – vers la borne + du générateur.Quantité d’électricitéL’unité de charge électrique est le COULOMB (C). La charge d’un électron est de : - 1,6 x 10-l 9 C.ElectrocinétiqueDr. Ing. Otman Aghzout3

4. +-École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueCourant électriqueLe sens de circulation conventionnel du courant électrique est de la borne + vers la borne - du générateur.L’unité d’intensité est I’AMPÈRE (A).Multiples :Le Kilo ampère : 1kA = 103 A.Sous-multiples :Le milliampère : l mA = 10-3 A.Le microampère : 1A = 10-6 A.Le nanoampère : 1nA = 10-9 A.ElectrocinétiqueDr. Ing. Otman Aghzout4

5. I = - 3mA+A+AI = 3mABB--École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueReprésentation d’un même courant électriqueDeux manières de représenter un courant de 3 mA circulant de A vers B.ElectrocinétiqueDr. Ing. Otman Aghzout5

6. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueI – Définitions sur les circuits électriques :1 – Réseaux et dipôles :Un réseau est un circuit électrique complexe, formé de fils conducteurs et de composants reliés à l’extérieur par 2 bornes (des dipôles).Des dipôles peuvent être placés en série :Dipôle 1Dipôle 2Ou en parallèle (en dérivation):Dipôle 1Dipôle 2ElectrocinétiqueDr. Ing. Otman Aghzout6

7. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétique2 – Maille, branche et nœud :Nœud : un nœud du réseau est un point d’interconnexion relié à au moins trois dipôles.Branche : une branche est une portion de circuit comprise entre deux nœuds. Elle peut comprendre un ou plusieurs dipôles placés en série.Maille : une maille est un ensemble de branches, formant une boucle fermée, qui ne passe qu’une fois par un nœud donné.ElectrocinétiqueDr. Ing. Otman Aghzout7

8. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueApplicationIntensité du courant dans un dipôleDéterminer les intensités I1 et I2 non précisées sur le schéma ci-dessous.B0.8 A1.2 AI1A-0.3 A0.7 AI2ElectrocinétiqueDr. Ing. Otman Aghzout8

9. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueApplicationIntensité du courant dans un dipôleSolution Les courants d’intensité o,8 A, 1,2 A et -0,3 A arrivant en A, alors que les courants d’intensité 0,7 A et I2Repartent de A . D’après la loi des nœuds:0,8+1,2-0,3=0,7+ I2, d’où: I2= 1 A De même, le courant d’intensité I1 arrive en B et les courants d’intensités 0,8 et 1,2 A repartent de B, D’après la loi des nœuds :I1=0,8+1,2=2 AElectrocinétiqueDr. Ing. Otman Aghzout9

10. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétique3 – Nature du courant électrique (dans les métaux) :Le courant électrique est dû à un mouvement d’ensemble des électrons de conduction. Intensité d’un courant électrique (dans un métal):I en ampères.Q en coulombs.t en secondes.On note dq la quantité de charges électriques qui circulent dans le sens positif choisi pendant l’intervalle de temps dt à travers la section transverse s du conducteur.L’intensité idu courant électrique est alors : ElectrocinétiqueDr. Ing. Otman Aghzout10

11. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueSi i > 0 : le courant va réellement de A vers B (et les électrons de B vers A).Si i < 0 : le courant va réellement de B vers A (et les électrons de A vers B, car dq < 0).Si i = cste = I, on parle de régime continu (indépendant du temps).A un instant donné, l’intensité d’un courant variable est la même tout le long d’un circuit sans dérivation : c’est l’approximation des régimes quasi-stationnaires (on néglige le temps de propagation du signal électrique).ElectrocinétiqueDr. Ing. Otman Aghzout11

12. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueApplicationCharge d’une batteriePour recharger une batterie, un chargeur délivre un courant d’intensité 5 mAsous une tension de 12 Vet fonctionne pendant 10 heures.Quelle quantité d’électricité circule dans les fils d’alimentation de la batterie lors de cette charge?Les porteurs de charge sont les électrons. Combien d’électrons ont circulé pendant cette charge?ElectrocinétiqueDr. Ing. Otman Aghzout12

13. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueApplicationCharge d’une batterieSolutionL’intensité du courant I=5 A est constante. La durée de la charge est t=10h =3,6.104 s . La quantité d’électricité circulant dans les fils d’alimentation vaut donc: Q=It=5.10-3 x 3,6.104 = 1,8.102 CLa valeur absolue de la charge d’un électron est e= 1,6.10-19 C. Pour avoir la charge Q, il a donc circulé dans les fils N électrons tels que:Q=Ne d’où : N=Q/e= 1,8.102 / 1,6.10-19 =1,1 1021 électronsElectrocinétiqueDr. Ing. Otman Aghzout13

14. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueII – Conventions de signe, caractéristiques de dipôles :1 – Conventions générateur et récepteur :iiDipôle Dipôle ABABConvention récepteurConvention générateurLe choix arbitraire des conventions n’indique pas pour autant le type de fonctionnement réel (générateur ou récepteur) du dipôle.Si deux dipôles sont reliés entre eux, les conventions sontnécessairement récepteur pour l’un et générateur pour l’autre.ElectrocinétiqueDr. Ing. Otman Aghzout14

15. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétique2 – Caractéristiques de conducteurs ohmiques, loi d’Ohm : iDipôle ohmique ABConvention récepteurDroite de pente RR est la résistance du conducteur (exprimée en ohm, W) G est la conductance du conducteur (exprimée en siemens, S)ElectrocinétiqueDr. Ing. Otman Aghzout15

16. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétique3 – Caractéristiques de générateurs (dipôles actifs linéaires) :iDipôle actif AB0Convention générateurCaractéristique linéaireL’équation de la caractéristique du dipôle actif linéaire est :ElectrocinétiqueDr. Ing. Otman Aghzout16

17. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiquetension à vide (i = 0) , mesurée avec un voltmètre. intensité de court-circuit , mesurée avec un ampèremètre.Le dipôle actif linéaire est ainsi équivalent aux deux éléments suivants :iOn note :ABDipôle actif AlorsConvention générateurElectrocinétiqueDr. Ing. Otman Aghzout17

18. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueiABDipôle actif Un générateur idéal de tension de fém notée e (égale à la tension à vide aux bornes du dipôle) en série avec Un conducteur ohmique de résistance r (résistance interne du dipôle actif).Cette modélisation du dipôle actif est appelée Convention générateur(modélisation de Thévenin)ElectrocinétiqueDr. Ing. Otman Aghzout18

19. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueiABUn générateur idéal de courant électromoteur (égal au courant de court-circuit du dipôle actif) en parallèle avec un conducteur ohmique de résistance r (résistance interne du dipôle actif).Cette modélisation du dipôle actif est appelée Convention générateurmodélisation de Norton ElectrocinétiqueDr. Ing. Otman Aghzout19

20. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueModélisationd’ungénérateurlinéaireOnpeututiliserlesdeuxmodèleséquivalentssuivants:Onpose E=U0 etR=U0/I0 et doncU=E-R.I Onpeutremplacerledipôleparunesource detensionidéaledef.e.m.Eensérieavec unerésistanceR.Modèle source de tensionIAREUABBElectrocinétiqueDr. Ing. Otman Aghzout20

21. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueModélisationd’ungénérateurlinéaireOnpeutremplacerledipôleparunesourcede courantidéaled’intensitéJenparallèleavec unerésistanceR.Modèle source de courantOnposeJ=I0etG=I0/U0etdonc: I=J-G.UIAG.UJBElectrocinétiqueDr. Ing. Otman Aghzout21

22. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueModélisationd’ungénérateurlinéaireCesdeuxreprésentationssontduales: G=1/RJ=E/R R=1/GE=R.JSilesdipôlesainsimodéliséssontdesgénérateurspurs,larésistanceRsenommela résistanceinternedugénérateur.Elleestnullepourungénérateurdetensionidéaletinfinie pourungénérateurdecourantidéal.Eestlaforceélectromotrice(f.e.m.)àvidec’est-à-dire sanschargeentreAetB.ElectrocinétiqueDr. Ing. Otman Aghzout22

23. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiquehttp://subaru2.univ-lemans.fr/enseignements/physique/02/electri/kirchhoff.html4 – Associations de dipôles :Associations de conducteurs ohmiques :En série :Les résistances s’ajoutent :En parallèle (en dérivation) :Les conductances s’ajoutent :soitElectrocinétiqueDr. Ing. Otman Aghzout23

24. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueApplicationTrouvez la représentation en circuit équivalente à la structure suivante:Trouvez la résistance équivalente RAentre A1 et A2 de même la résistance équivalente RB entre B1 et B2ElectrocinétiqueDr. Ing. Otman Aghzout24

25. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueApplicationLa résistance équivalente entre A1 et A2 est : RA = 65 WLa résistance équivalente entre B1 et B2est : RB = 57,6 W2.Solution1.A1A1A1A1A1RAA2A2A2A2A2ElectrocinétiqueDr. Ing. Otman Aghzout25

26. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueAssociations de dipôles actifs linéaires :En série (choix du modèle de Thévenin) :Les fém s’ajoutent (algébriquement) et les résistances internes s’additionnent.ir1r2ABe1e2iréqABeéqElectrocinétiqueDr. Ing. Otman Aghzout26

27. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueAssociations de dipôles actifs linéaires :En parallèle (choix du modèle de Norton) :Les courants électromoteurs s’ajoutent (algébriquement) et les conductances s’additionnent.ElectrocinétiqueDr. Ing. Otman Aghzout27

28. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueAssociations de dipôles actifs linéaires :En parallèle (choix du modèle de Norton) :Les courants électromoteurs s’ajoutent (algébriquement) et les conductances s’additionnent.ElectrocinétiqueDr. Ing. Otman Aghzout28

29. RabÉcole Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueThéorème de KennellyLe théorème de Kennelly, permet la transformation d’un montage de dipôles de type triangle en montage de type étoile ou visse versa. Ce théorème est utile dans le cas où l’on souhait simplifier des schémas. En réalité il s’agit surtout d’équations simples permettant une équivalence de montage.Montage TriangleMontage étoileABABRanRbnnRcbRacRcnCCElectrocinétiqueDr. Ing. Otman Aghzout29

30. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueApplicationThéorème de KennellyTrouvez la représentation en circuit équivalente à la structure suivante:ElectrocinétiqueDr. Ing. Otman Aghzout30

31. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueApplicationThéorème de KennellyNous allons simplifier le schéma en remplacent l’étoile (Ra, Rb et Rc) par un triangle (Rf, Rg et Rh). Parfois les montages sont très complexes ainsi il faut procéder méthodiquement, marquer les points de l’étoile (points verts), rayer les trois résistances à modifier puis relier les points avec de nouvelles résistances (Rf, Rg et Rh).Nous notons la disparition du nœud central de l’étoile (point rouge), attention Kennelly ne s’applique pas si ce nœud est connecté à un 4éme élément.ElectrocinétiqueDr. Ing. Otman Aghzout31

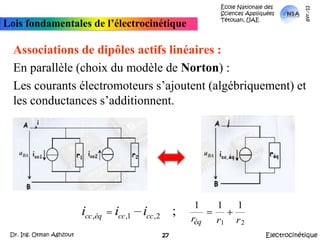
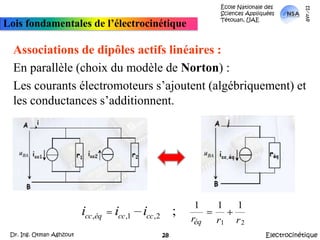
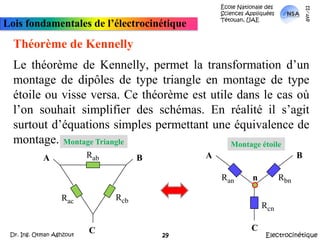
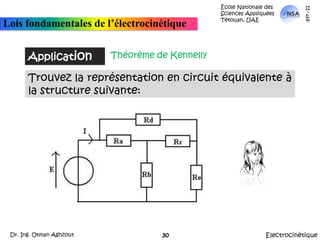
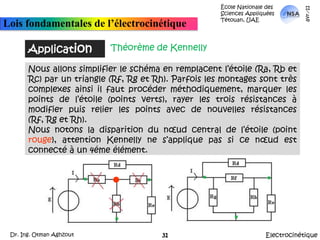
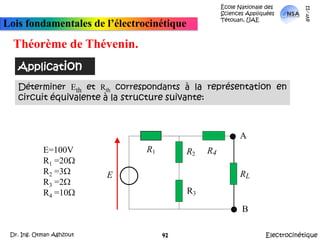
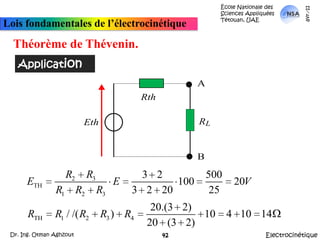
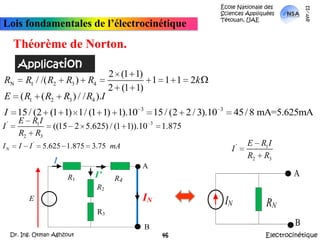
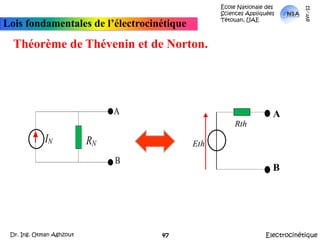
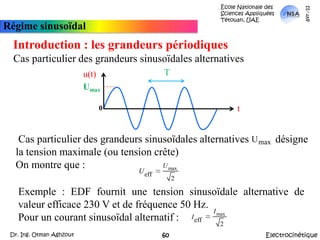
32. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueApplicationThéorème de KennellyA partir de là, Réq = {[(Rd parallèle Rf) en série avec (Rh parallèle Re)] parallèle Rg}.Autrement: Réq = {[(Rd //Rf) + (Rh//Re)]//Rg}ElectrocinétiqueDr. Ing. Otman Aghzout32

33. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueThéorème de MillmanIl permet de trouver le potentiel d'un point du circuit lorsqu'on connaît les autres.ElectrocinétiqueDr. Ing. Otman Aghzout33

34. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueThéorème de MillmanLa démonstration est immédiate à l'aide de la modélisation par un ensemble de 3 générateurs en parallèle :ElectrocinétiqueDr. Ing. Otman Aghzout34

35. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueThéorème de PouilletiEBAUBAElectrocinétiqueDr. Ing. Otman Aghzout35

36. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueEffet JouleUn courant électrique est un déplacement d'électrons libres dans un matériau conducteur. Lorsqu'ils se déplacent les électrons entrent en collision avec les atomes formant le matériau et donc ceux-ci se mettent à vibrer. Ces atomes étant liés entre eux, les vibrations s'amplifient dans tout le matériau, et donc sa température (qui est une mesure de leur agitation) augmente.Cet échauffement du conducteur lors du passage du courant électrique s'appelle l'effet Jouleplaques de cuissonradiateur électriqueGrille-painfer à repasser

37. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueEffet JouleEnergie électrique ou travailLe déplacement d’une charge Q entre deux points A et B avec VA et VB les potentiels correspondants, s’accompagnent du travail électrique :Puissance électriqueSi le déplacement se fait à travers une résistance R.ElectrocinétiqueDr. Ing. Otman Aghzout37

38. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueEffet JouleEnergie électrique ou travailLa loi de Joule décrit le phénomène de l'effet Joule :l'énergie calorique (en joule) dégagée par un conducteur électrique de résistance R (en ohm) traversé par un courant I (en ampère) pendant un temps t (en seconde) est donnée par la relation suivante :Loi de joule.Le travail par unité de temps est la puissance :ElectrocinétiqueDr. Ing. Otman Aghzout38

39. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueThéorème de Thévenin et de Norton.Toute portion de circuit comprise entre 2 bornes A et B et qui ne contient que des éléments linéaires peut être modélisée par un unique générateur équivalent de Thévenin ou de Norton. Exemple :ElectrocinétiqueDr. Ing. Otman Aghzout39

40. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueThéorème de Thévenin.Valeur à donner à ETHC'est la même que la valeur de la tension existant "à vide" entre A et B, c'est à dire celle que relèverait un voltmètre idéal placé entre les bornes A et B.Pour l'exemple précédent on a :diviseur de tension.ElectrocinétiqueDr. Ing. Otman Aghzout40

41. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueThéorème de Thévenin.ApplicationDéterminer Eth et Rth correspondants à la représentation en circuit équivalente à la structure suivante:E=100VR1 =20WR2 =3WR3 =2WR4 =10WElectrocinétiqueDr. Ing. Otman Aghzout41

42. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueThéorème de Thévenin.ApplicationElectrocinétiqueDr. Ing. Otman Aghzout42

43. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueThéorème de Norton.Valeur à donner à INC'est celle de l'intensité qui circulerait à travers un fil reliant les bornes A et B c'est à dire celle mesurée par un ampèremètre idéal placé entre A et B.Dans notre exemple on obtient :INsoit : (R2 étant court-circuitée.)ElectrocinétiqueDr. Ing. Otman Aghzout43

44. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueThéorème de Norton.Pour calculer le circuit Norton équivalent :On calcule le courant entre les bornes A et B (IAB), quand les bornes A et B sont court-circuitées, c'est-à-dire quand la charge est nulle entre A et B. Ce courant est IN.La tension de sortie VAB est calculée, quand aucune charge externe n'est connectée c'est-à-dire avec une résistance infinie entre A et B. RN est égal à VAB divisé par IN.Le circuit équivalent consiste en une source de courant INen parallèle avec une résistance RN.ElectrocinétiqueDr. Ing. Otman Aghzout44

45. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueThéorème de Norton.ApplicationDéterminer IN et RN correspondant à la représentation en circuit équivalente à la structure suivante:E=15VR1 =2kWR2 =1kWR3 =1kWR4 =1kWElectrocinétiqueDr. Ing. Otman Aghzout45

46. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueThéorème de Norton.ApplicationElectrocinétiqueDr. Ing. Otman Aghzout46

47. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Lois fondamentales de l’électrocinétiqueThéorème de Thévenin et de Norton.ElectrocinétiqueDr. Ing. Otman Aghzout47

48. Electrocinétique IIRégime sinusoïdalDr. Ing. Otman Aghzout

49. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Régime sinusoïdalIntroduction : les grandeurs périodiques Période Un signal périodique est caractérisé par sa période :Tu(V)10 V24T=2mst(ms)01.5ElectrocinétiqueDr. Ing. Otman Aghzout49

50. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Régime sinusoïdalIntroduction : les grandeurs périodiquesFréquenceLa fréquence f (en hertz) correspond au nombre de périodes par unité de temps :A.N.T = 2 ms f = 500 Hz (500 périodes par seconde)PulsationLa pulsation est définie par : (en radians par seconde)ElectrocinétiqueDr. Ing. Otman Aghzout50

51. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Régime sinusoïdalIntroduction : les grandeurs périodiquesLa plus grande partie de sa courte vie fut consacrée à la recherche scientifique. Dans le but de donner une base expérimentale à la théorie électromagnétique de la lumière, mise en équations par maxwell , Hertz étudia systématiquement les champs électrique et magnétique crées par des circuits oscillants de capacité et d'inductance de plus en plus petites. Il parvint ainsi, en 1888, à mettre en évidence l'existence d'ondes électromagnétiques très courtes grâce à son " résonateur". La mesure directe de leurs longueurs d'onde lui permit de vérifier que la célérité de leur propagation est, conformément aux prévisions de maxwell, égale à celle de la lumière. En 1885, Hertz découvrit l'effet photoélectrique en montrant qu' une plaque de zinc électrisée se décharge lorsqu'elle reçoit de la lumière ultraviolette .HEINRICH HERTZ RUDOLF. Physicien allemand, né à Hambourg en 1857 et mort à Bonn en 1894.ElectrocinétiqueDr. Ing. Otman Aghzout51

52. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Régime sinusoïdalIntroduction : les grandeurs périodiques Valeur moyenneOn note <u> la valeur moyenne dans le temps de la tension u(t) :u(t)10 V<u>=2.5 Vt00.75TTElectrocinétiqueDr. Ing. Otman Aghzout52

53. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Régime sinusoïdalIntroduction : les grandeurs périodiques Composante continue (DC =) et composante alternative (AC ~)Une grandeur périodique a deux composantes :la composante continue (c’est la valeur moyenne ou «offset»)

54. et la composante alternativecomposante continue u(t)=10 V02.5 V0ttcomposante alternative u(t) = <u> + u AC(t) +7.5 V0t-2.5 V

55. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Régime sinusoïdalIntroduction : les grandeurs périodiques Remarques : la composante alternative a une valeur moyenne nulle : <u AC> = 0 une grandeur périodique alternative n’a pas de composante continue : <u> = 0ElectrocinétiqueDr. Ing. Otman Aghzout54

56. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Régime sinusoïdalIntroduction : les grandeurs périodiquesPuissance électriquedipôleABp(t)=u(t)×i(t)est la puissance électrique consommée à l’instant t (ou puissance instantanée).En régime périodique, ce n’est pas p(t) qu’elle est intéressant de connaître mais la puissance moyenne dans le temps :Attention : en général, ElectrocinétiqueDr. Ing. Otman Aghzout55

57. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Régime sinusoïdalIntroduction : les grandeurs périodiquesValeur efficacePar définition, la valeur efficace Ueff de la tension u(t) est :u2(t)100 V2.75TT<u2>=25 V2t0ElectrocinétiqueDr. Ing. Otman Aghzout56

58. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Régime sinusoïdalIntroduction : les grandeurs périodiques Remarques :La valeur efficace est une grandeur positive.Valeur efficace d’un courant électrique :ElectrocinétiqueDr. Ing. Otman Aghzout57

59. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Régime sinusoïdalIntroduction : les grandeurs périodiquesSignification physique de la valeur efficaceSoit une résistance parcourue par un courant continu :RLa résistance consomme une puissance électrique(loi de Joule)ElectrocinétiqueDr. Ing. Otman Aghzout58

60. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Régime sinusoïdalIntroduction : les grandeurs périodiquesSoit la même résistance parcourue par un courant périodique i(t) devaleur efficaceRABLa puissance moyenne consommée est :Pour avoir les mêmes effets thermiques, il faut que Ieff soit égal à la valeur du courant en régime continu I (idem pour les tensions) :La notion de valeur efficace est liée à l’énergie.ElectrocinétiqueDr. Ing. Otman Aghzout59

61. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Régime sinusoïdalIntroduction : les grandeurs périodiques Cas particulier des grandeurs sinusoïdales alternativesTu(t)Umaxt0 Cas particulier des grandeurs sinusoïdales alternatives désigne la tension maximale (ou tension crête)On montre que :Exemple : EDF fournit une tension sinusoïdale alternative de valeur efficace 230 V et de fréquence 50 Hz.Pour un courant sinusoïdal alternatif :ElectrocinétiqueDr. Ing. Otman Aghzout60

62. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Régime sinusoïdalIntroduction : les grandeurs périodiquesApplicationCalculer la valeur efficace de la tension suivante :20VElectrocinétiqueDr. Ing. Otman Aghzout61

63. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Régime sinusoïdalReprésentation des grandeurs sinusoïdalesFonction mathématiqueavec : : valeur efficace (A) : pulsation (rad/s)t : temps (s) : phase (rad) : phase à l’origine (rad)ElectrocinétiqueDr. Ing. Otman Aghzout62

64. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Régime sinusoïdalReprésentation des grandeurs sinusoïdalesReprésentation de FresnelC’est une représentation vectorielle des grandeurs sinusoïdales.Le vecteur de Fresnel associé au courant i(t) est défini de la façon suivante :+Axe d’origine des phasesx0ElectrocinétiqueDr. Ing. Otman Aghzout63

65. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Régime sinusoïdalReprésentation des grandeurs sinusoïdalesNombre complexe associéLe nombre complexe I associé au courant i(t) est défini de la façon suivante :ElectrocinétiqueDr. Ing. Otman Aghzout64

66. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Régime sinusoïdalReprésentation des grandeurs sinusoïdalesApplicationDéterminer le nombre complexe associé à la tension :ElectrocinétiqueDr. Ing. Otman Aghzout65

67. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Régime sinusoïdalDéphasage (ou différence de phase) entre deux grandeurs sinusoïdalesSoit deux grandeurs sinusoïdales (de même fréquence) :Le déphasage de u par rapport à i est par convention :t : décalage (en s) entre les deux signaux.ElectrocinétiqueDr. Ing. Otman Aghzout66

68. École Nationale des Sciences Appliquées Tétouan, UAEmars-11Régime sinusoïdalDéphasage (ou différence de phase) entre deux grandeurs sinusoïdalesDéphasages particuliers déphasage nul (t = 0) :les grandeurs sont en phase déphasage de 180°(t = T/2) :les grandeurs sont en opposition de phase déphasage de 90° (t = T/4) :grandeurs en quadrature de phaseN.B. Le déphasage est une grandeur algébrique : : uest en quadrature avance sur i.ElectrocinétiqueDr. Ing. Otman Aghzout67