Le document fournit un cours d'électrocinétique sur les circuits électriques en régime stationnaire, abordant des concepts tels que le courant, la tension, la loi d'Ohm, ainsi que les méthodes d'analyse des circuits. Il détaille également les dipôles actifs et passifs, les sources d'énergie, et inclut des explications sur les instruments de mesure comme les voltmètres et ampèremètres. Des exercices sont intégrés tout au long du document pour renforcer la compréhension des concepts présentés.

































![3 – Méthodes d’étude d’un circuit électrique en régime permanent
37
On isole tout d’abord la branche AB à travers laquelle circule l’intensité que l’on veut cal-
culer. Pour cela, on retrace le circuit en mettant clairement en évidence les associations
en parallèle et en série. On reconnaît en effet les associations suivantes :
• le générateur de f.é.m. et le résistor sont en série ;
• le générateur de f.é.m. et le résistor sont en série ;
• les générateurs de Thévenin et sont en parallèle.
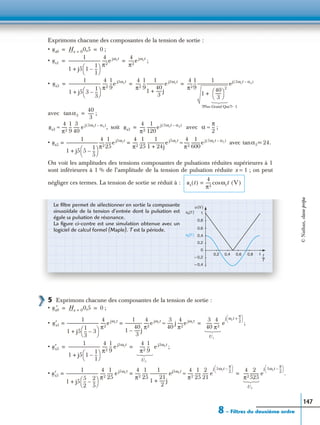
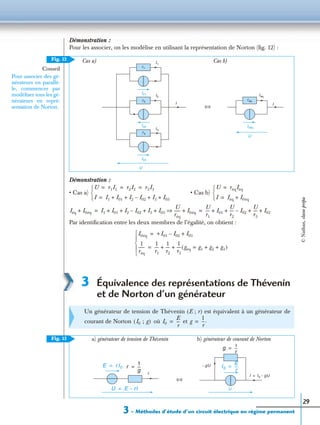
2 – Étude d’un circuit comportant
un potentiomètre
Considérons un réseau constitué de 2 générateurs
idéaux de f.é.m. et alimentant une même
résistance r. Le circuit est fermé par l’intermé-
diaire d’un potentiomètre CD et muni d’un cur-
seur B réalisant un contact mobile dont la
position est caractérisée par un paramètre réel
La résistance totale de la branche C
et D est R, le curseur sépare la partie CB (résis-
tance de la partie BD (résistance
Calculer l’intensité I du courant circulant dans la branche centrale du circuit.
E2E1
A
B
C D
R
xR 1 x–( )R
I
r
E1 E2
x 0 ; 1[ ]∈ .
xR), 1 x–( )R).
résolution méthodique
On ne cherche que la valeur d’une seule intensité, la méthode de réduction du circuit est donc
bien adaptée. On pourrait aussi utiliser la loi des nœuds en terme de potentiel mais nous ne la
traitons pas dans cette correction.
E1 xR
E2 1 x–( )R
E1 ; xR( ) E2 ; 1 x–( )R( )
Prendre l’habitude de refaire les schémas pour :
– faire apparaître clairement les associations série et parallèle ;
– distinguer clairement la branche AB du réseau qui l’alimente.
E2E1 r
A
B
C D
xR 1 x–( )R
E
F
G
H
I
©Nathan,classeprépa](https://image.slidesharecdn.com/electrocintiqueclasspr-160118183523/85/Electrocinetique-class-prepas-37-320.jpg)







![4 – Circuits RC, RL, RLC série soumis à un échelon de tension
49
2. Solution particulière de l’équation différentielle complète :
3. Solution générale de l’équation complète.
a. Régime apériodique
b. Régime pseudo-périodique
ou
c. Régime critique
4. Conditions initiales imposées au circuit
À la fermeture de l’interrupteur (date :
• la tension aux bornes du condensateur ne subit pas de discontinuité. S’il est initialement
déchargé, alors : D’où :
• l’intensité du courant qui traverse la bobine ne subit pas de discontinuité donc :
On en déduit les valeurs des constantes dans chacun des cas.
a. Régime apériodique
;
;
Si le discriminant est positif ; le régime est apériodique.
Si le discriminant est négatif ; le régime est pseudo-périodique.
Si le discriminant est nul ; le régime est critique.
• Exprimer la solution de l’équation caractéristique.
Si les solutions sont réelles : et
Si les solutions sont complexes. On pose : avec
D’où : et
Si la solution est double :
• Exprimer la solution de l’équation différentielle sans second membre.
Si alors avec et constantes réelles.
Si alors avec et constantes
réelles, ou avec et constantes réelles.
Si alors avec et constantes réelles.
σ 1Ͼ Q
1
2
---Ͻ
,
σ 1Ͻ Q
1
2
---Ͼ
,
σ 1= Q
1
2
---=
,
Remarque
Le régime critique est
un cas limite sans réa-
lité physique car la
valeur de σ ne peut
être exactement égale
à 1.
σ 1,Ͼ r1 σ– ∆+= r2 σ– ∆.–=
σ 1,Ͻ ∆ j 2 ∆–= j 2 1.–=
r1 σ– j ∆–+= r2 σ– j ∆–+=
σ 1,= r1 r2 1.–= =
σ 1,Ͼ yssm A1er1x
A2er2x
+= A1 A2
σ 1,Ͻ yssm e σx– B1 ∆– x( )cos B2 ∆– x( )sin+[ ]= B1 B2
yssm B ′e σx– ∆– x ϕ+( )cos= B ′ ϕ
σ 1,= yssm e x– C1x C2+[ ]= C1 C2
yp 1.=
σ 1Ͼ( )
y 1 A1er1x
A2er2x
.+ +=
σ 1Ͻ( )
y 1 e σx– B1 ∆– x( )cos B 2 ∆– x( )sin+[ ]+= y 1 B ′e σx– ∆– x ϕ+( ).cos+=
σ 1=( )
y 1 e x– C1x C2+[ ].+=
t 0+)=
u 0( ) 0.= y 0( ) 0.=
i 0( ) C
du
dt
------
0( )
0
dy
dx
------
0( )
⇒ 0.= = =
y 0( ) 1 A1 A2+ + 0= =
dy
dx
------
0( )
r1A1 r2A2+ 0= =
A1⇒
r2
r1 r2–
---------------= A2
r1
r1 r2–
---------------.–=
©Nathan,classeprépa](https://image.slidesharecdn.com/electrocintiqueclasspr-160118183523/85/Electrocinetique-class-prepas-49-320.jpg)
![retenir l’essentiel
50
b. Régime pseudo-périodique
;
;
c. Régime critique
;
La solution complète de l’équation différentielle s’écrit :
a. Régime apériodique
b. Régime pseudo-périodique
c. Régime critique
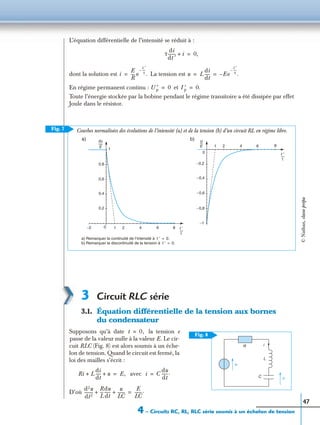
3.3. Évolution de la tension et de l’intensité
Il suffit de remplacer, dans les équations précédentes, x par et y par
a. Régime apériodique
;
b. Régime pseudo-périodique
;
L’expression fait apparaître la pseudo-pulsation :
Pseudo-période :
c. Régime critique
;
L’expression de l’intensité se déduit de celle de la tension par la relation
y 0( ) 1 B1+ 0= =
dy
dx
------
0( )
σB1– 1 σ2– ; B2+ 0= =
B1 1–=⇒ B2
σ
1 σ2–
-------------------.–=
y 0( ) 1 C2+ 0= =
dy
dx
------
0( )
C2– C1+ 0= =
C2⇒ C1 1– .= =
y 1
σ σ2 1–+
2 σ2 1–
-----------------------------e σ– σ2 1–+( )x σ– σ2 1–+
2 σ2 1–
---------------------------------e σ– σ2 1––( )x.––=
y 1 e σx– 1 σ2– x( )cos
σ
1 σ2–
------------------- 1 σ2– x( )sin+ .–=
y 1 e x– x 1+[ ]–= .
ω0t
u
E
----.
σ 1Ͼ Q
1
2
---Ͻ
u
E
---- 1
σ σ2 1–+
σ2 1–
-----------------------------e σ– σ2 1–+( )ω0t σ– σ2 1–+
σ2 1–
---------------------------------e σ– σ2 1––( )ω0t
.+ +=
σ 1Ͻ Q
1
2
---Ͼ
u
E
---- 1 e σω0t–
ω0 1 σ2– t( )cos
σ
1 σ2–
------------------- ω0 1 σ2– t( )sin+–=
ω ω0 1 σ2– .=
T
2π
ω
------
2π
ω0 1 σ2–
--------------------------
T0
1 σ2–
-------------------.= = =
σ 1= Q
1
2
---=
u
E
---- 1 e ω0t–
ω0t 1+[ ].–=
i C
du
dt
------.=
Électrocinétique PCSI, MPSI, PTSI - © Nathan, Classe prépa
©Nathan,classeprépa](https://image.slidesharecdn.com/electrocintiqueclasspr-160118183523/85/Electrocinetique-class-prepas-50-320.jpg)






![savoir résoudre les exercices
58
La loi des nœuds permet d’écrire :
3 Écrivons les différentes relations entre les grandeurs qui vont nous servir :
(loi des nœuds), et (loi d’Ohm).
Il vient :
Ce qui conduit à :
4 Divisons l’équation par LC :
On peut alors identifier les termes recherchés :
et et
Remarque : Un circuit RLC série devient idéal quand ; il se réduit alors à un circuit
.
Pour réduire à un circuit LC un circuit RLC parallèle il faut que On comprend
alors que les expressions du facteur de qualité de chacun des circuits soient inverses l’une
de l’autre.
Le régime est pseudo-périodique car l’amortissement est inférieur à 1 (facteur de qualité
supérieur à 0,5).
i0+ i R0+ i L0++ i R0+ 20 mA( )= = =
i i L i R+= i C–
du
dt
------,= u L
diL
dt
--------,= u Ri R=
Il faut mettre un signe moins car le condensateur est en convention générateur.
u L
di L
dt
--------- L
d
dt
----- i i R–[ ] L
d
dt
----- C–
du
dt
------
u
R
---– L C–
d2u
dt 2
---------
1
R
---
du
dt
------– .= = = =
LC
d2u
dt 2
---------
L
R
---
du
dt
------ u+ + 0=
d2u
dt 2
---------
1
RC
--------
du
dt
------
u
LC
-------+ + 0.=
ω0
1
LC
------------ 3,1 103 rad s 1–· ·= =
2ω0σ
1
RC
-------- ⇒= σ
1
2R
-------
L
C
---- 0,16= = Q
1
2σ
------- R
C
L
---- 3,16= = =
Les expressions de et de Q ne sont pas celles du circuit RLC série car les trois composants sont en
parallèle. En série, alors que,
σ
Qsérie
Lω0
R
--------
1
R
---
L
C
----,= = Qparallèle
1
Qsérie
-----------
R
Lω0
--------.= =
R 0=
LC
R ∞.=
Électrocinétique PCSI, MPSI, PTSI - © Nathan, Classe prépa
©Nathan,classeprépa](https://image.slidesharecdn.com/electrocintiqueclasspr-160118183523/85/Electrocinetique-class-prepas-58-320.jpg)
![4 – Circuits RC, RL et RLC série soumis à un échelon de tension
59
5 Voir § 3.2 de « Retenir l’essentiel » pour établir l’équation différentielle réduite.
Appliquons la méthode donnée dans « Retenir l’essentiel » (point méthode 2) pour
résoudre l’équation différentielle.
a. Solution générale.
• Équation caractéristique :
Discriminant réduit :
• Solutions : et avec et
Les solutions sont complexes, le régime est pseudopériodique.
• Solution de l’équation différentielle :
avec A et B constantes réelles.
b. Détermination des constantes en écrivant les conditions initiales imposées au circuit, à
savoir :
• Continuité de la tension aux bornes du condensateur :
• Continuité de l’intensité du courant qui traverse la bobine :
Il faut chercher D’après la deuxième question, la condition implique
Par ailleurs et ;
donc D’où :
c. Solution de l’équation différentielle
Une équation différentielle réduite (sous forme canonique) ne contient que des termes sans
dimensions. Cela simplifie sa résolution.
r2 2σr 1+ + 0.=
∆ σ2 1– 0,98– ?Moi= =
r 1
σ– j ∆–+= r 2
σ– j ∆– ,+= ∆ j2 ∆–= j2 1.–=
y e σx– A ∆– x( )cos B ∆– x( )sin+[ ],=
ut 0+= ut 0–= U0 yx 0=⇒ 1 A⇒ 1.= = = =
iL0+ 0.=
dy
dx
------
0+
. iL0+ 0=
i0+ iR0+
u0+
R
-------
U0
R
------.= = = i0+ C
du
dt
------
0+
–=
du
dt
------
d U0y( )
d
x
ω0
------
------------------ U0ω0
dy
dx
------= =
dy
dx
------
0+
1
Cω0
----------
du
dt
------
0+
–
i0+
Cω0U0
------------------–
1
RCω0
---------------– 2σ.–= = = =
dy
dx
------
0
σA– B ∆–+ 2σ– B⇒
σ–
∆–
-----------.= = =
C’est bien en écrivant la continuité de l’intensité du courant qui traverse la bobine que l’on
détermine la constante B. Mais ici, comme parfois, la détermination de la relation entre les
constantes est indirecte.
y e σx– ∆– x( )cos
σ
∆–
----------- ∆– x( )sin– .=
La résolution d’une équation différentielle du second ordre sans second membre impose l’intro-
duction de deux constantes :
Il faut écrire la solution complète de l’équation différentielle avant de déterminer les constantes.
Les constantes sont déterminées en écrivant les continuités :
– de la tension aux bornes des condensateurs,
– et de l’intensité du courant qui traverse les bobines.
©Nathan,classeprépa](https://image.slidesharecdn.com/electrocintiqueclasspr-160118183523/85/Electrocinetique-class-prepas-59-320.jpg)
![savoir résoudre les exercices
60
A.N. :
Sachant que et que il vient :
L’expression de l’intensité se déduit de la relation
On vérifie qu’à la date l’intensité est égale à 20 mA.
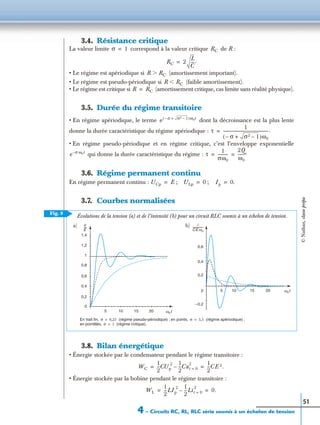
6 Les courbes sont tracées ci-dessous.
y e 0,158x– 0,987x( )cos 0,16 0,987x( )sin–[ ].=
Il faut maintenant revenir à la fonction en utilisant les relations etu t( ) x ω0t= u U0 y.=
ω0 3,1 103 rad s 1–· ·= U0 20 V,=
u t( ) 20e 5,0– 102t· 3,1 103t·( )cos 0,16 3,1 103t·( )sin–[ ] V( )=
i C–
du
dt
------.=
i t( ) e 5,0– 102t· 20 3,1 103t·( )cos 60 3,1 103t·( )sin+[ ] mA( )=
t 0=
20
u V( ) i A( )
t s( ) t s( )
15
10
5
0
−5
−10
0,002 0,0020,006 0,0060,01 0,01
0
0,01
0,02
0,03
0,04
0,05
−0,01
−0,02
−0,03
0,004 0,0080,004 0,008
• Une équation différentielle réduite (sous forme canonique) ne contient que des
termes sans dimension. Cela simplifie sa résolution.
• La résolution d’une équation différentielle du second ordre sans second membre
impose l’introduction de deux constantes.
Il faut écrire la solution complète de l’équation différentielle avant de déterminer les
constantes.
Les constantes sont déterminées en écrivant les continuités :
– de la tension aux bornes des condensateurs,
– et de l’intensité du courant qui traverse les bobines.
• Le facteur de qualité Q d’un circuit RLC parallèle s’écrit Q
R
Lω0
---------.=
en conclusion
Électrocinétique PCSI, MPSI, PTSI - © Nathan, Classe prépa
©Nathan,classeprépa](https://image.slidesharecdn.com/electrocintiqueclasspr-160118183523/85/Electrocinetique-class-prepas-60-320.jpg)

![savoir résoudre les exercices
62
3 Appliquons la méthode donnée dans « Retenir l’essentiel » (point méthode 2) pour
résoudre l’équation différentielle.
a. Solution générale de l’équation différentielle.
• Équation caractéristique :
• Posons avec Les solutions sont complexes :
et
• Solution de l’équation différentielle :
avec A et B constantes réelles.
b. Détermination des constantes en écrivant les conditions initiales imposées au circuit, à
savoir :
• Continuité de la tension bornes du condensateur :
• Continuité de l’intensité du courant qui traverse la bobine :
c. Solution de l’équation différentielle : ;
A.N. :
L’expression de l’intensité se déduit de la relation En effet :
A.N. :
4 L’énergie du circuit est la somme des énergies des deux composants :
⇒
L’énergie totale est constante. Elle est égale à l’énergie initialement stockée dans le conden-
sateur.
r2 ω0
2
+ 0 r2⇒ ω0
2
.–= =
r2 j2ω0
2
= j2 1.–=
r 1
jω0= r 2
jω0.–=
u A ω0t( )cos B ω0t( ),sin+=
ut 0+= ut 0–= U0 A⇒ U0.= = =
i0+ i0– 0.= =
i0+ C
du
dt
------
0+
– 0
du
dt
------
0
⇒ ω0B 0 B⇒ 0.= = = = =
u U0 ω0t( )cos=
u t( ) 20 1,0 104t·( ) V( )cos=
i C–
du
dt
------.=
i C–
du
dt
------ CU0ω0 ω0t( )sin= =
i t( ) 0,20 1,0 104t·( ) A( )sin=
Le régime d’un circuit LC est sinusoïdal.
w wC wL+
1
2
---Cu2 1
2
---Li 2+
1
2
---C U0 ω0t( )cos[ ]2 1
2
---L CU0ω0 ω0t( )sin[ ]2+= = =
w
1
2
---CU0
2
ω0t( )cos[ ]2 ω0t( )sin[ ]2+( )=
w
1
2
---CU0
2
0,20 mJ= =
Un circuit LC est un oscillateur électrique ; la tension et l’intensité sont des fonctions
sinusoïdales du temps.
L’énergie d’un circuit LC est constante ; elle est alternativement stockée par le con-
densateur et par la bobine. C’est un circuit idéal, sans réalité physique.
en conclusion
Électrocinétique PCSI, MPSI, PTSI - © Nathan, Classe prépa
©Nathan,classeprépa](https://image.slidesharecdn.com/electrocintiqueclasspr-160118183523/85/Electrocinetique-class-prepas-62-320.jpg)














![5 – Circuits linéaires en régime sinusoïdal forcé
79
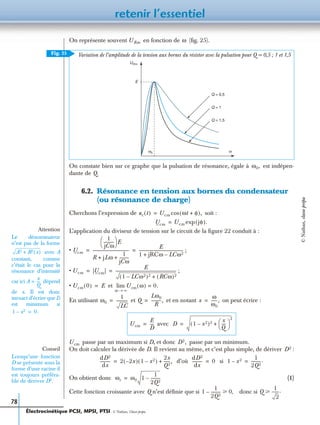
La courbe passe donc par un maximum pour On parle de résonance
de tension aux bornes du condensateur ou de résonance de charge car la charge du
condensateur est proportionnelle à la tension.
Il y a deux différences importantes entre la résonance d’intensité et la résonance de
charge : la résonance de charge n’existe que pour des valeurs de Q suffisamment grandes
et quand elle existe, la pulsation de résonance dépend de Q.
Le calcul conduit à (2)
On constate bien sûr sur ce graphe qu’il n’y a pas de résonance si
et que la pulsation de résonance est d’autant plus grande que Q est grand
6.2.1. Étude du déphasage
La courbe représentant en fonction de se déduit donc de la courbe représentant
par un simple décalage vers le bas de donc
Variation de l’amplitude de la tension aux bornes du condensateur avec la pulsation pour Q = 0,5 ; 1
et 1,5.
Variation de la phase de la tension aux bornes du condensateur avec la pulsation
Ucm ω( ) Q
1
2
-------.уAttention
Les résonances d’in-
tensité et de charge
sont très différentes, il
ne faut pas les confon-
dre. Une erreur fré-
quente consiste par
exemple à écrire qu’il
y a résonance de
charge pour ωr ω0.= Ucm ωr( )
QE
1
1
4Q2
---------–
-----------------------.=
Uc m
ωr1 ω
Q = 1,5
Q = 1
Q = 0,5
ωr1,5
Fig. 26
Q 0,5= (Q
1
2
-------Ͻ 0,71)=
ωr1 ωr1,5Ͻ( ).
Ucm
1
jCω
----------
Icm φ⇒ ϕ
π
2
---–= =
φ ω ϕ
π
2
---,– φ 0 ; π–[ ].∈
0
ω0 ω
π
2
---–
π–
φ(rad)
Fig. 27
©Nathan,classeprépa](https://image.slidesharecdn.com/electrocintiqueclasspr-160118183523/85/Electrocinetique-class-prepas-79-320.jpg)


![savoir résoudre les exercices
82
et avec
; et puisque on a :
On a donc avec
• R et sont des impédances ;
• ;
•
L’amplitude de la tension est bien homogène à une tension et est sans dimension.
A.N. :
ou
Pour connaître la bonne valeur de évaluons :
;
Transformation d’une grandeur complexe en grandeur réelle
Connaissant avec
• L’amplitude de de est le module de l’amplitude complexe
• La phase de est l’argument de
x t( ) Xm
jωt( ),exp= x t( ) Xm ωt ϕ+( ).cos=
Xm x t( ) Xm
.
ϕ x t( ) Xm
.
Im | Im| ⇒= Im
Em
R 2 1
Cω
--------
2
+
----------------------------------=
ϕ Imarg ϕ⇒ ϕ′–= = ϕ′ R
1
jCω
----------+
arg R
j
Cω
--------–
arg= =
ϕ′tan
1
Cω
--------–
R
------------
1
RCω
------------–= = ϕ–( )tan ϕ,tan–=
ϕtan
1
RCω
------------=
i t( )
Em
R 2 1
Cω
--------
2
+
---------------------------------- ωt ϕ+( ),cos= ϕtan
1
RCω
------------.=
Vérifier l’homogénéité des expressions obtenues.
1
Cω
--------
Im[ ]
Em[ ]
Z[ ]2 Z[ ]2+
--------------------------------
Em[ ]
Z[ ]
------------= =
ϕ( )tan[ ]
Z[ ]
Z[ ]
--------.=
ϕtan
Im
10
1,0 103·( )2 1
0,16 10 6–· 63 102·×
----------------------------------------------------
2
+
--------------------------------------------------------------------------------------------------- 7,1 mA.= =
ϕtan
1
1,0 103· 0,16 10 6– 63 102·×·×
------------------------------------------------------------------------------- 1 ϕ⇒
π
4
---= = =
5π
4
------.
ϕ, ϕcos
Im
Em
R
1
jCω
----------+
--------------------
Em R
j
Cω
--------+
R2 1
Cω
--------
2
+
-------------------------------- Im ϕcos j ϕsin+( )= = =
Électrocinétique PCSI, MPSI, PTSI - © Nathan, Classe prépa
©Nathan,classeprépa](https://image.slidesharecdn.com/electrocintiqueclasspr-160118183523/85/Electrocinetique-class-prepas-82-320.jpg)
![5 – Circuits linéaires en régime sinusoïdal forcé
83
donc
Donc
2 Avec les mêmes notations qu’au 1., la loi de Pouillet donne donc :
et avec
puisque on a :
On a donc avec
• R et sont des impédances ;
• ;
•
L’amplitude de l’intensité est bien homogène à une intensité et est sans dimension.
A.N. :
ou
Pour connaître la bonne valeur de évaluons :
donc
Donc
ϕcos
R
R 2 1
Cω
--------
2
+
---------------------------------- 0,Ͼ= ϕ
π
4
---.=
i t( ) mA( ) 7,1 63 102t
p
4
---+·
.cos=
Im
Em
R jLω+
--------------------,=
Im | Im| ⇒= Im
Em
R 2 Lω( )2+
---------------------------------=
ϕ Imarg ϕ⇒ ϕ′–= = ϕ′ R jLω+( )arg=
ϕ′tan
Lω
R
--------,= ϕ–( )tan ϕ,tan–=
ϕtan
Lω
R
--------–=
i t( )
Em
R 2 Lω( )2+
--------------------------------- ωt ϕ+( ),cos= ϕtan
Lω
R
--------.–=
On vérifie l’homogénéité des expressions obtenues.
Lω
Im[ ]
Em[ ]
Z[ ]2
---------------
Em[ ]
Z[ ]
------------= =
ϕ( )tan[ ]
Z[ ]
Z[ ]
--------.=
ϕtan
Im
10
1,0 103·( )2 0,091 63× 102·( )2+
-------------------------------------------------------------------------------------- 8,7 mA= =
ϕtan
0,091 63× 102·
1,0 103·
---------------------------------------– 0,57– ϕ⇒
π
6
---–= = =
5π
6
------.
ϕ, ϕcos
Im
Em
R jLω+
--------------------
Em R jLω–( )
R 2 Lω( )2+
--------------------------------- Im ϕcos j ϕsin+( )= = =
ϕcos
R
R 2 Lω( )2+
--------------------------------- 0Ͼ= ϕ
π
6
---–=
i t( ) mA( ) 8,7cos 63 102t
p
6
---–·
.=
©Nathan,classeprépa](https://image.slidesharecdn.com/electrocintiqueclasspr-160118183523/85/Electrocinetique-class-prepas-83-320.jpg)


![savoir résoudre les exercices
86
1 a. Le générateur, le résistor, le condensateur et la bobine
étant en parallèle, la tension est la même
aux bornes de chacun d’eux.
Soit et
• avec ;
• ;
•
Vérification de l’homogénéité
est le rapport entre l’impédance d’une bobine et celle d’un condensateur,
c’est donc une grandeur sans dimension ;
;
b. et
qui est une grandeur positive, passe
donc par un maximum. Cherchons pour
quelle valeur de
L’expression de obtenue au 1. a. com-
porte le facteur à la fois au numérateur et
au dénominateur, ce qui rend l’étude de la
recherche du maximum plus difficile que
dans le cas étudié en cours pour le circuit
RLC série. On peut facilement simplifier
l’étude en divisant le numérateur et le déno-
minateur par On obtient :
Cette fraction est maximale si le dénominateur est minimal, donc si :
soit
résolution méthodique
i 0 u
u Um ωt ϕ+( )cos=
Um
Um jϕ( )exp= I0m I0m.=
I0m Y Um
,= Y
1
R
---
1
jLω
--------- jCω+ +=
Um
I0m
1
R
---
1
jLω
--------- jCω+ +
-------------------------------------
I0mR jLω
jLω R R LCω2–+
----------------------------------------------
I0mRLω
Lω jR 1 LCω2–( )–
------------------------------------------------= = =
Um | Um
|
I0mRLω
L2ω2 R 2 1 L Cω2–( )2
+
---------------------------------------------------------------.= =
L Cω2 Lω
1
Cω
--------
-------------=
Um[ ]
I0m[ ] Z[ ]2
Z[ ]2
------------------------- I0m[ ] Z[ ]= =
ϕ( )tan[ ]
Z[ ]
Z[ ]
--------.=
Um
Ummax
ωω0
Ummax
2
----------------
Um 0( ) 0= Um 0=
ω ∞→
lim
Um,
ω.
Um
ω
ω.
Um | Um
|
I0mRL
L2 R 2 1
ω
---- L Cω–
2
+
-------------------------------------------------------.= =
1
ω
---- L Cω– 0,= ω ω0
1
L C
------------.= =
Électrocinétique PCSI, MPSI, PTSI - © Nathan, Classe prépa
©Nathan,classeprépa](https://image.slidesharecdn.com/electrocintiqueclasspr-160118183523/85/Electrocinetique-class-prepas-86-320.jpg)
![5 – Circuits linéaires en régime sinusoïdal forcé
87
c.
Les solutions positives (seules pertinentes) de ces deux équations sont :
et
Vérification de l’homogénéité des relations de type :
• le rapport est bien sans dimension (rapport entre deux impédances au carré).
Remarque : On peut aussi vérifier l’homogénéité de cette dernière relation en remarquant
que est homogène à un temps, comme En effet, une pulsation est homogène à
l’inverse d’un temps
•
Remarque : On peut aussi vérifier l’homogénéité de cette dernière relation directement en
remarquant que RC est homogène à un temps.
On remarque que ce facteur de qualité est l’inverse de celui d’un circuit RLC série. En
fait, dans les deux cas, un facteur de qualité infini correspond à un circuit non amorti,
constitué uniquement d’une bobine idéale et d’un condensateur. En effet,
• Quand on obtient une fonction comportant à la fois au numérateur et au dénominateur,
on essaye, lorsque c’est possible, de simplifier afin que seul le dénominateur dépende de
Il est alors plus simple de chercher la valeur de pour laquelle cette fonction est extrémale.
• Quand le dénominateur se présente sous la forme avec A constant, cette fonction
est minimale quand est minimale. Assez souvent, pour obtenir le minimum, il suffit de cher-
cher la valeur de pour laquelle est nul. Si ce n’est pas possible, il faut dériver la fonction.
ω
ω.
ω
A2 B2 ω( )+
B2 ω( )
ω B ω( )
Um ω0( ) Ummax RI0m= =
Um ω1 ω2,( )
Ummax
2
---------------
L
L2 R 2 1
ω
---- L Cω–
2
+
-------------------------------------------------------⇒
1
2
-------= =
2L2 L2 R 2(
1
ω
---- LCω)2–+ L = R
1
ω
---- LCω–
±⇒=
Lω± R RLCω2– RLCω2 Lω± R–⇒ 0.= =
ω1
1
2RC
-----------–
∆
2RLC
---------------+
1
2RC
----------- 1– 1
4R 2
L2ω0
2
------------++
= =
ω2
1
2RC
-----------
∆
2RLC
---------------+
1
2RC
----------- 1 1
4R 2
L2ω0
2
------------++
.= =
Q
ω0
∆ω
--------
ω0
ω2 ω1–
------------------- RCω0
R
Lω0
----------= = = = ⇒ Q
R
Lω0
----------=
ω1
1
2RC
-----------–
∆
2RLC
---------------+
1
2RC
----------- 1– 1
4R 2
L2ω0
2
------------++
.= =
4R 2
L2ω0
2
------------
L
R
---
1
ω0
------.
ω
2π
T
------=
.
1
Cω
-------- R[ ] ω[ ]⇒
1
2RC
----------- .= = ©Nathan,classeprépa](https://image.slidesharecdn.com/electrocintiqueclasspr-160118183523/85/Electrocinetique-class-prepas-87-320.jpg)
![6 – Puissance en régime sinusoïdal forcé
retenir l’essentiel
89
Puissance
en
régime sinusoïdal forcé
1 Puissance instantanée et puissance moyenne
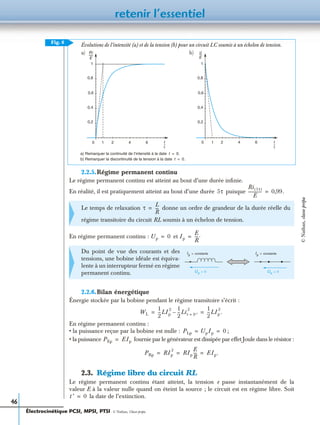
1.1. Notations utilisées
Considérons un dipôle D linéaire représenté
en convention récepteur (figure 1).
On note
et
où R est la résistance du dipôle
et S sa réactance,
On peut écrire R et S en fonction de Z et :
En utilisant la loi d’ohm en représentation complexe, on a :
est l’avance de phase de la tension sur l’intensité (déphasage).
1.2. Puissance instantanée
Le dipôle D reçoit la puissance instantanée (convention récepteur).
(1)
Fig. 1
i(t)
u(t)
u t( ) Um ωt ϕu+( )cos=
i t( ) Im ωt ϕi+( ).cos=
Z R jS,+=
Z Zexp jϕ( )=
ϕ
R Z ϕcos=
S Z ϕsin=
Um Z Im=
ϕu ϕ ϕi+=
ϕ
p t( ) u t( ) i t( )=
p t( ) Um ωt ϕu+( )Imcos ωt ϕi+( )cos=
UmIm
2
--------------- 2ωt ϕu ϕi+ +( )cos ϕu ϕi–( )cos+[ ]=
UmIm
2
--------------- 2ωt ϕu ϕi+ +( )cos ϕ( )cos+[ ]=
©Nathan,classeprépa](https://image.slidesharecdn.com/electrocintiqueclasspr-160118183523/85/Electrocinetique-class-prepas-89-320.jpg)
![retenir l’essentiel
90
Cette puissance varie au cours du temps (figure 2) de façon sinusoïdale (pulsation
autour de la valeur
1.3. Puissance moyenne – Facteur de puissance
On verra sur des exemples (exercice 2) que dans de nombreuses applications, la grandeur
pertinente n’est pas la puissance instantanée, mais la puissance moyenne :
En effet, la valeur moyenne d’une fonction sinusoïdale est nulle (voir exercice 1 de
« S’entraîner », chapitre 5) et celle d’un terme constant est évidemment égale à ce terme.
Le terme est appelé facteur de puissance.
Remarque : La puissance moyenne est aussi appelée puissance active.
1.4. Autre expression de la puissance moyenne,
valeur efficace
Nous serons parfois amenés à utiliser une autre expression de
Or donc :
Seule la partie réelle R (la résistance) de l’impédance complexe intervient dans l’expression
de la puissance moyenne reçue.
Point maths. On a utilisé la formule
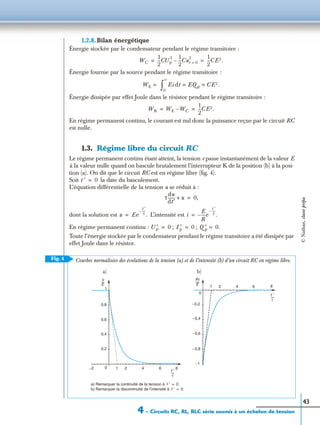
Variation de la puissance instantanée
La puissance moyenne s’écrit :
a( )cos b( )cos
1
2
--- a b+( )cos a b–( )cos+[ ].=
2ω)
ᏼmoy
UmIm
2
--------------- ϕ( ).cos=
p t( )
t
p(t)
ᏼmoy
Fig. 2
ᏼmoyAttention
On ne peut pas direc-
tement utiliser les
grandeurs complexes
et pour cal-
culer il faut uti-
liser les grandeurs
réelles et
Nous développerons
cette remarque dans
l’exercice 4 de « Tester
ses connaissances ».
u t( ) i t( )
p t( ),
u t( ) i t( ).
ᏼmoy p t( )〈 〉
UmIm
2
--------------- 2ωt ϕu ϕi+ +( )cos〈 〉 ϕ( )cos〈 〉+[ ].= =
ᏼmoy
UmIm
2
--------------- ϕ( ).cos=
ϕ( )cos
ᏼmoy .
Um ZIm ᏼmoy⇒
UmIm
2
--------------- ϕ( )cos
Im
2
2
------Z ϕ( ).cos= = = Z ϕ( )cos R ,=
ᏼmoy
RIm
2
2
-----------.=
Électrocinétique PCSI, MPSI, PTSI - © Nathan, Classe prépa
©Nathan,classeprépa](https://image.slidesharecdn.com/electrocintiqueclasspr-160118183523/85/Electrocinetique-class-prepas-90-320.jpg)









![7 – Transfert d’un système linéaire – Filtres du premier ordre
101
1.6. Filtre
Un filtre idéal est un quadripôle linéaire pour lequel la tension de sortie est nulle dans un
domaine de fréquences caractéristique.
Un filtre réel est un quadripôle linéaire pour lequel la tension de sortie est atténuée dans
un domaine de fréquences caractéristique.
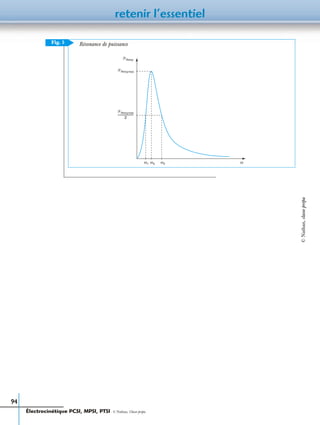
2 Diagramme de Bode d’un filtre
2.1. Forme réduite de la fonction de transfert d’un filtre
2.2. Diagramme de Bode d’un filtre
Le diagramme de Bode est la représentation de la fonction de transfert d’un filtre.
Il est constitué de deux courbes :
• la courbe de réponse en gain, exprimé en décibels, en fonction de
;
• la courbe de réponse en phase en fonction de
On peut aussi tracer les courbes et en fonction du loga-
rithme décimal de la valeur numérique de noté
Amplificateur opérationnel (AO) en régime linéaire
• x est la pulsation réduite, ou fréquence réduite, avec
• est la pulsation caractéristique du filtre, f 0 est la fréquence caractéristique.
Point maths. L’expression « » désigne le logarithme décimal de x.
Point maths. L’échelle logarithmique. Décade
L’axe des abscisses de chacune des courbes et est gradué en échelle loga-
rithmique (figure 3). Les valeurs de x sont en général représentées par décades (
1, …).
Une décade est l’intervalle de fréquence tel que :
Fig. 2
us
i+ 0=
ε 0=
u+
u–
+
−
i− 0=
• Le courant d’entrée inverseuse – est nul.
• Le courant d’entrée non inverseuse + est nul.
• La tension différentielle ε est nulle.
Remarque. L’alimentation en énergie électrique n’est pas
représentée.
H jx( )
us
ue
----- H x( ) ejϕ x( )= =
x
ω
ω0
------
f
f0
-----.= =
ω0
H jx( )
G x( ) 20log H jx( )=
log x( )
ϕ x( ) log x( ).
log x( )
G ω( ) 20log H jω( )= ϕ ω( )
ω, log ω( ).
Attention
Le point d’abscisse
n’apparaît pas
sur le diagramme
de Bode puisque
x 0=
log 0( ) ∞.–=
G x( ) ϕ x( )
…10 3– ,
10 2– , 10 1– , 101, 102, 103
f1 ; f2[ ]
f2
f1
----- 10.=
©Nathan,classeprépa](https://image.slidesharecdn.com/electrocintiqueclasspr-160118183523/85/Electrocinetique-class-prepas-101-320.jpg)


![7 – Transfert d’un système linéaire – Filtres du premier ordre
105
3.6. Bande passante à –3 dB
Exemple du filtre passe-bas du premier ordre :
• Détermination de la valeur maximale du module de la fonction de transfert :
• Résolution de l’équation :
4 Filtre passe-haut du premier ordre
4.1. Fonction de transfert
Le terme en d’ordre 1, est celui dont l’ordre est le plus élevé d’où le nom de premier
ordre donné au filtre. Nous travaillerons dans la suite avec la valeur
Point méthode. Détermination de la bande passante à –3 dB d’un filtre
a) Déterminer la valeur maximale du module de la fonction de transfert.
b) Résoudre l’équation Selon le cas, on travaille avec la pulsation, la
fréquence ou la fréquence réduite.
• Autre méthode : déterminer la valeur maximale Gmax du gain, puis résoudre l’équa-
tion
La bande passante à –3 dB d’un filtre passe-bas du premier ordre de fréquence de
coupure est :
Fonction de transfert et forme réduite de la fonction de transfert
d’un filtre passe-haut du premier ordre :
;
• est la pulsation de coupure et est la fréquence de coupure.
• est une constante réelle.
H max
H
H max
2
----------------.=
G Gmax 3.–=
H max
Hmax Hx 0= 1.= =
H jx( ) 1
1 jx+
--------------
1
1 x2+
-------------------
Hmax
2
------------- x⇒ 1 f⇒ fc.= = = = =
fc
∆f 0 ; fc[ ].=
H jω( ) H jx( )
H jω( ) A0
j
ω
ωc
------
1 j
ω
ωc
------+
----------------- A0
j
f
fc
----
1 j
f
fc
----+
---------------= = H jx( ) A0
jx
1 jx+
--------------.=
ωc fc
A0
ω
ωc
------,
A0 1.=
©Nathan,classeprépa](https://image.slidesharecdn.com/electrocintiqueclasspr-160118183523/85/Electrocinetique-class-prepas-105-320.jpg)

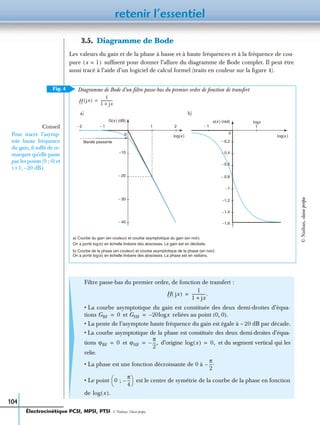
![7 – Transfert d’un système linéaire – Filtres du premier ordre
107
4.5. Diagramme de Bode
Remarque :
La courbe de réponse en phase du filtre passe-haut se déduit de celle du filtre passe-bas
par translation positive de le long de l’axe des phases.
a) Courbe du gain (en couleur) et courbe asymptotique du gain (en noir).
On a porté log(x ) en échelle linéaire des abscisses. Le gain est en décibels.
b) Courbe de la phase (en couleur) et courbe asymptotique de la phase (en noir).
On a porté log(x ) en échelle linéaire des abscisses. La phase est en radians.
Filtre passe-haut du premier ordre, de fonction de transfert
• La courbe asymptotique du gain est constituée des deux demi-droites d’équa-
tions et reliées au point
• La pente de l’asymptote basse fréquence du gain est égale à +20 dB par décade.
• La courbe asymptotique de la phase est constituée des deux demi-droites d’équations
et d’origine et du segment vertical qui les relie.
• La phase est une fonction décroissante de à 0.
• Le point est le centre de symétrie de la courbe de la phase en fonction
de
Fig. 5
G(x) (dB)
log(x)
ϕ(x) (rad)
1
1,2
0,8
0,6
−10
−20
−30
−40
Bande passante
a)
− 2 − 1 1 2
log(x)
b)
0,2
0,4
1,4
0
0
− 2 − 1 1
1,0
Diagramme de Bode d’un filtre passe-haut du premier ordre de fonction de transfert H jx( )
jx
1 jx+
--------------=
Conseil
Pour tracer l’asymp-
tote basse fréquence
du gain, il suffit de re-
marquer qu’elle passe
par les points (0 ; 0) et
(−1 ; −20 dB).
H jx( )
jx
1 jx+
--------------.=
GBF 20log x( )= GHF 0= 0 ; 0( ).
ϕBF
π
2
---= ϕHF 0,= log x( ) 0,=
π
2
---
0 ;
π
4
---
log x( ).
H jx( )[ ]passe
haut
jx
1 jx+
-------------- jx
1
1 jx+
-------------- xe
j
π
2
---
H jx( )[ ]passe
bas
ϕ x( )[ ]passe
haut
⇒
π
2
--- ϕ x( )[ ]passe
bas
+= = = =
π
2
---
©Nathan,classeprépa](https://image.slidesharecdn.com/electrocintiqueclasspr-160118183523/85/Electrocinetique-class-prepas-107-320.jpg)














![savoir résoudre les exercices
122
5
Aussi petite que soit la valeur de la tension le terme varie de manière monotone ;
il y a donc saturation de la sortie ; le montage ne peut pas fonctionner en intégrateur.
6 a. Appliquons la loi des nœuds en termes de
potentiels (théorème de Millmann) au point A,
de potentiel nul (figure ci-contre) :
avec :
b. Le filtre a un caractère intégrateur si on peut écrire :
ce qui implique :
c. La condition avec donne :
A.N. :
d. Une tension de décalage E en entrée provoque, en régime permanent, une tension de
décalage en sortie d’expression :
A.N. :
Il n’y a donc pas de saturation en sortie ; le montage fonctionne en intégrateur pour des
fréquences supérieures à 100 Hz.
us
1
τ
---–= ε f t( )+[ ]dt
1
τ
---–=
0
t
∫ f t( )dt ε
t
τ
--– .
0
t
∫
ε, ε–
t
τ
--
ue
+
−
E
R
A
S
C
R
us
uA
1
R′
----- jCω
1
R
---+ +
uE
R
-----
1
R′
----- jCω+
uS+ 0= =
H jω( )
us
ue
-----
1
R
R′
----- jRCω+
---------------------------–
R′
R
-----–
1
1 jωτ′+
--------------------,= = =
A0
R′
R
-----–=
H jω( )
R′
R
-----–
1
jωτ′
----------
1
jωτ
--------– ,= =
ωτ′ Ͼ1Ͼ
f
fc′
---- 10Ͼ f 100 Hz=
f′c 10 2πR′C⇒Ͻ
1
10
------.Ͼ
R′ 16 kΩϾ .
Us
Us H ω 0=( )E
R′
R
-----E.–= =
Us 1,6 mV– .=
En régime permanent, une tension d’entrée constante peut-être considérée comme une
tension sinusoïdale de fréquence nulle (période infinie). La tension de sortie correspondante
s’écrit :
Ue
Us
Us H ω 0=( )Ue.=
Électrocinétique PCSI, MPSI, PTSI - © Nathan, Classe prépa
©Nathan,classeprépa](https://image.slidesharecdn.com/electrocintiqueclasspr-160118183523/85/Electrocinetique-class-prepas-122-320.jpg)





![8 – Filtres du deuxième ordre
129
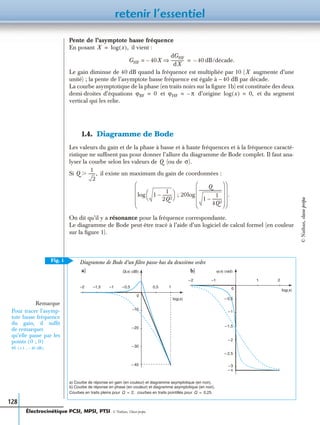
2 Filtre passe-bande du deuxième ordre
2.1. Fonction de transfert
2.2. Courbe de réponse en phase
Nous travaillons dans la suite avec la valeur
Filtre passe-bas du deuxième ordre, de fonction de transfert :
• La courbe asymptotique du gain est constituée des deux demi-droites d’équa-
tions et reliées au point
• La pente de l’asymptote haute fréquence du gain est égale à –40 dB par décade.
• Si il existe une résonance de pulsation réduite
• La courbe asymptotique de la phase est constituée des deux demi-droites d’équations
et d’origine et du segment vertical qui les relie.
• La phase est une fonction décroissante de 0 à
• Le point est le centre de symétrie de la courbe de la phase en fonction
de
La fonction de transfert d’un filtre passe-bande du deuxième ordre est :
• est la pulsation propre (ou pulsation de résonance) du filtre et la fréquence
propre (ou fréquence de résonance).
• est le facteur de qualité, est l’amortissement, avec
• est une constante réelle.
La forme réduite de la fonction de transfert d’un filtre passe-bande du deuxième
ordre est :
avec
• Autre forme :
H jx( )
1
1 j
x
Q
--- jx( )2+ +
----------------------------------.=
GHF 0= GBF 40– log x( )= 0 ; 0( ).
Q
1
2
-------,Ͼ xr 1.Ͻ
ϕBF 0= ϕHF π,–= log x( ) 0,=
π.–
0 ;
π
2
---–
log x( ).
H jω( ) A0
j
1
Q
---
ω
ω0
------
1 j
1
Q
---
ω
ω0
------ j
ω
ω0
------
2
+ +
---------------------------------------------- A0
j2σ
f
f0
----
1 j2σ
f
f0
---- j
f
f0
----
2
+ +
----------------------------------------------.= =
ω0 f0
Q σ σ
1
2Q
-------.=
A0
H jx( ) A0
j
x
Q
---
1 j
x
Q
--- jx( )2+ +
---------------------------------- A0
2jσx
1 2jσx jx( )2+ +
-----------------------------------------,= = x
ω
ω0
------
f
f0
----.= =
H jx( ) A0
1
1 jQ x
1
x
---–
+
----------------------------------- A0
1
1
j
2σ
------- x
1
x
---–
+
----------------------------------.= =
A0 1.=
H jx( )[ ] passe
bande
j
x
Q
---
1
1 j
x
Q
--- jx( )2+ +
---------------------------------- e
j
π
2
--- x
Q
--- H jx( )[ ]passe
bas
ϕ x( )[ ] passe
bande
π
2
--- ϕ x( )[ ]passe
bas
+=⇒= =
©Nathan,classeprépa](https://image.slidesharecdn.com/electrocintiqueclasspr-160118183523/85/Electrocinetique-class-prepas-129-320.jpg)


![retenir l’essentiel
132
3 Filtre passe-haut du deuxième ordre
3.1. Fonction de transfert et forme réduite
3.2. Courbe de réponse en phase
Nous travaillons dans la suite avec la valeur
La courbe de réponse en phase du filtre passe-haut se déduit de celle du filtre passe- bande
du deuxième ordre par translation positive de le long de l’axe des phases.
La courbe asymptotique de la phase (en traits noirs sur la figure 4b) est constituée des
deux demi-droites d’équations et d’origine et du seg-
ment vertical qui les relie.
La fonction de transfert d’un filtre passe-haut du deuxième ordre est :
• est la pulsation caractéristique du filtre et la fréquence caractéristique.
• est le facteur de qualité, est l’amortissement, avec
• est une constante réelle.
La forme réduite de la fonction de transfert d’un filtre passe-haut du deuxième
ordre est :
avec
H jω( ) A0
j
ω
ω0
------
2
1 j
1
Q
---
ω
ω0
------ j
ω
ω0
------
2
+ +
--------------------------------------------- A0
j
f
f0
----
2
1 j2σ
f
f0
---- j
f
f0
----
2
+ +
----------------------------------------------.= =
ω0 f0
Q σ σ
1
2Q
-------.=
A0
H jx( ) A0
jx( )2
1 j
x
Q
--- jx( )2+ +
---------------------------------- A0
jx( )2
1 j2σx jx( )2+ +
-----------------------------------------,= = x
ω
ω0
------
f
f0
----.= =
A0 1.=
H jx( )[ ]passe
haut
jQx
j
x
Q
---
1 j
x
Q
--- jx( )2+ +
----------------------------------=
e
j
π
2
---
Qx H jx( )[ ] passe
bande
ϕ x( )[ ]passe
haut
⇒
π
2
--- ϕ x( )[ ] passe
bande
+= =
π
2
---
ϕBF π= ϕHF 0,= log x( ) 0,=
Électrocinétique PCSI, MPSI, PTSI - © Nathan, Classe prépa
©Nathan,classeprépa](https://image.slidesharecdn.com/electrocintiqueclasspr-160118183523/85/Electrocinetique-class-prepas-132-320.jpg)


![8 – Filtres du deuxième ordre
135
d’où l’équation différentielle :
5.2. Stabilité du système
5.2.1. Stabilité du système en régime libre
Le système est stable en régime libre si la solution de la solution de l’équation diffé-
rentielle converge vers zéro quand t tend vers l’infini.
Nous l’écrirons sous la forme pour l’étude suivante.
• Équation caractéristique de l’équation différentielle :
• Soient et les solutions, avec et
• Discriminant de l’équation caractéristique :
a. Cas où le discriminant est positif
La solution et constantes) de l’équation différentielle converge
vers zéro si et sont négatives, ce qui impose et Les
deux inégalités sont satisfaites si et sont du même signe.
b. Cas où le discriminant est négatif
Dans ce cas ; a et c sont du même signe.
Les solutions de l’équation caractéristique s’écrivent :
et avec
La solution avec A et B constantes réelles, converge vers
zéro si donc si b et a sont du même signe. Au total, a, b et c doivent être du même signe.
c. Cas où le discriminant est nul
Dans ce cas (relation 1).
La solution de l’équation caractéristique est double :
La solution avec et constantes réelles, converge vers zéro
si (relation 2). Les relations 1 et 2 imposent que , et soient du même signe.
Dans les trois cas, la solution converge vers zéro si a, b et c sont du même signe.
Un système du second ordre est stable en régime libre si les coefficients
et (resp. et du dénominateur de la fonction de transfert :
(resp. )
sont du même signe.
D2
d2us
dt2
---------- D1
dus
dt
-------- D0us+ + N2
d2ue
dt2
----------- N1
due
dt
-------- N0ue.+ +=
usL
D2
d2usL
dt2
------------- D1
dusL
dt
---------- D0usL+ + 0=
a
d2usL
dt2
------------- b
dusL
dt
---------- cusL+ + 0=
ar2 br c+ + 0.=
r1 r2 r1 r2+
b
a
--–= r1r2
c
a
--.=
∆ b2 4ac.–=
usL A1er1t
A2er2t
+= (A1 A2
r1 r2
b
a
-- r1– r2– 0Ͼ= r1r2
c
a
-- 0.Ͼ=
a, b c
∆ b2 4ac– 0 4ac⇒Ͻ b2 0Ͼ Ͼ=
r1
b– ∆––
2a
------------------------
b
2a
------– jΩ–= = r1
b– ∆–+
2a
------------------------
b
2a
------– jΩ,+= = Ω
∆–
2a
-----------.=
usL e
b
2a
------t–
A Ωt( )cos B Ωt( )sin+[ ],=
b
a
-- 0Ͼ
∆ b2 4ac– 0 4
a
b
--⇒
b
c
--= = =
r1 r2
b
2a
------.–= =
usL e
b
2a
------t–
A′t B′)+[ ],= A′ B′
b
a
-- 0Ͼ a b c
usL
D0, D1
D2 D ′0, D ′1 D ′2)
H jω( )
N0 jωN1 jω( )2N2+ +
D0 jωD1 jω( )2D2+ +
--------------------------------------------------------= H jx( )
N′0 N′1 jx N′2 jx( )2+ +
D ′0 D′1 jx D′2 jx( )2+ +
----------------------------------------------------=
©Nathan,classeprépa](https://image.slidesharecdn.com/electrocintiqueclasspr-160118183523/85/Electrocinetique-class-prepas-135-320.jpg)






![savoir résoudre les exercices
142
Le point M est à la masse donc Il vient :
Finalement :
3 Par identification avec la relation donnée au § 2.1 du cours, il vient :
On remarque que
4 Le gain est maximal quand le module de la fonction de transfert
est maximal soit pour
5 La pulsation caractéristique du filtre est telle que d’où :
6 Appliquons la méthode de détermination de la bande passante donnée au chapitre 7.
• Valeur maximale du module de la fonction de transfert :
et
us
1
R
--- jCω
1
R
1
jCω
----------+
--------------------+ +
1
R
--- uM jCω uM
1
R
1
jCω
----------+
--------------------ue.+ +=
uM 0.=
us
1
R
--- jCω
1
R
1
jCω
----------+
--------------------+ +
1
R
1
jCω
----------+
--------------------ue=
us
1 jx+
R
--------------
jCω
jx+1
------------+
jCω
jx+1
------------ue
us
R
---- 1 jx
jx
jx+1
------------+ +⇒
jx
jx+1
------------
ue
R
-----= =
us 1 jx+( )2 jx+[ ]⇒ jxue.=
H
1
3 j x
1
x
---–
+
-----------------------------=
La méthode du diviseur de tension est plus simple et plus rapide ; elle doit être préférée.
Q
1
3
---=
A0
1
3
---.=
H
1
9 x
1
x
---–
2
+
-----------------------------=
x 1.=
H max
1
3
---= Gmax G x 1=( ) 20log
1
3
---
9,5 dB–= = =
ω0 x 1,=
RCω0 RC 2πf0 1 ⇒= = f0
1
2πRC
--------------- 0,16 kHz= =
H max
1
3
---.=
Électrocinétique PCSI, MPSI, PTSI - © Nathan, Classe prépa
©Nathan,classeprépa](https://image.slidesharecdn.com/electrocintiqueclasspr-160118183523/85/Electrocinetique-class-prepas-142-320.jpg)

![savoir résoudre les exercices
144
On en déduit les équations des asymptotes haute fréquence :
et
b. La courbe asymptotique du gain est constituée des deux demi-droites qui se coupent
au point de coordonnées
Les courbes asymptotiques du gain et de la phase en fonction de sont en traits
noirs sur les figures ci-dessous.
c. Les quelques valeurs du gain et de la phase du tableau suivant permettent de tracer l’allure
du diagramme de Bode. On peut aussi utiliser un logiciel de calcul formel (figures ci-dessous).
Remarque : Les valeurs montrent que les courbes sont symétriques par rapport aux axes
verticaux.
9
En remplaçant, d’une part l’expression par et d’autre part l’expression par
il vient :
x 0,1 x1 = 0,3 1 x1 = 3,3 10
log(x) −1 −0,52 0 0,52 1
G (x) (en dB) −20 −12,5 −9,5 −12,5 −20
j (en rad) 1,3 0,78 0 −0,78 −1,3
GHF 20– log x( )= ϕHF
π
2
---.–=
0 ; 0( ).
log x( )
a. Gain b. Phase
G (x )
1
log (x)
0,50– 0,5– 1
– 5
(dB)
– 10
– 15
– 20
Q (x )
log (x)
1
(rad)
0
– 1
– 1,5
– 0,5– 1–1,5 0,5 1 1,5
log (x2)log (x1)
3 dB
π
4
---–
π
4
---
H jx( )
jx
1 3jx jx( )2+ +
-------------------------------------
jωτ
1 3jωτ jωτ( )2+ +
---------------------------------------------= = 1 3jωτ jωτ( )2+ +[ ]us⇒ jωτue=
jω
d
dt
----- jx( )2 d2
dt2
--------,
us 3τ
dus
dt
-------- τ2
d2us
dt2
----------+ + τ
due
dt
--------.=
L’équation différentielle d’un système du deuxième ordre se déduit de la fonction de transfert en
remplaçant chaque terme par l’opérateur et chaque terme par l’opérateurjω
d
dt
----- jω( )2 d2
dt2
-------.
Électrocinétique PCSI, MPSI, PTSI - © Nathan, Classe prépa
©Nathan,classeprépa](https://image.slidesharecdn.com/electrocintiqueclasspr-160118183523/85/Electrocinetique-class-prepas-144-320.jpg)