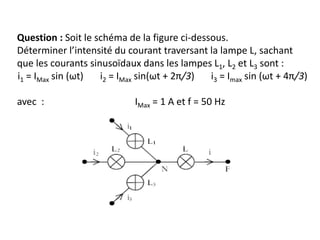
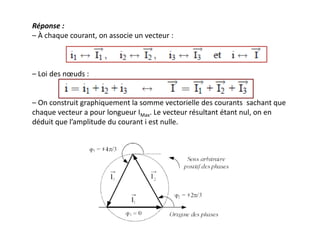
Le document traite du régime sinusoïdal permanent dans les circuits électriques linéaires où les grandeurs sont sinusoïdales synchrones avec la source. Il décrit des méthodes de calcul, notamment via la construction vectorielle de Fresnel et l'utilisation de nombres complexes, en abordant l'impédance et l'admittance complexes. Enfin, il souligne l'importance du facteur de puissance pour l'efficacité énergétique et les implications de la puissance active et réactive dans les systèmes alimentés.

1. Chapitre 1 :
RÉGIME SINUSOÏDAL PERMANENT :
MÉTHODES DE CALCULS

2. Lorsqu’un circuit électrique linéaire (composé de dipôles
linéaires) est alimenté en permanence par une source
d’énergie électrique sinusoïdale, les grandeurs
électriques du circuit sont toutes sinusoïdales de même
fréquence égale à celle de la source. On dit alors que
l’on est en régime sinusoïdal forcé et établi ou régime
sinusoïdal permanent.
Bien entendu, les calculs sur les valeurs instantanées
restent possibles, mais ils deviennent vite délicats. Afin
de faciliter les calculs, on utilise deux outils, qui font
abstraction du temps : le formalisme complexe, ou la
construction vectorielle de Fresnel.

3. Attention !
Les lois générales de l’électricité
(Les lois des nœuds, des mailles et
les théorèmes de Superposition,
Thévenin, Norton, Millmann, etc.) ,
restent valables à condition de les
appliquer aux valeurs instantanées,
ou bien, de les transposer au calcul
complexe ou au calcul vectoriel.

4. 1- Construction vectorielle de Fresnel
Méthode : À chaque grandeur sinusoïdale on
associe un vecteur, et réciproquement

5. Question : Soit le schéma de la figure ci-dessous.
Déterminer l’intensité du courant traversant la lampe L, sachant
que les courants sinusoïdaux dans les lampes L1, L2 et L3 sont :
i1 = IMax sin (ωt) i2 = IMax sin(ωt + 2π/3) i3 = Imax sin (ωt + 4π/3)
avec : IMax = 1 A et f = 50 Hz

6. Réponse :
– À chaque courant, on associe un vecteur :
– Loi des nœuds :
– On construit graphiquement la somme vectorielle des courants sachant que
chaque vecteur a pour longueur IMax. Le vecteur résultant étant nul, on en
déduit que l’amplitude du courant i est nulle.

7. 2- Utilisation des nombres complexes
Afin de faciliter les calculs, on associe une fonction
complexe du temps u = u (t) à chaque grandeur réelle
sinusoïdale du temps u = u (t). Si la grandeur est un sinus
(respectivement cosinus), alors elle est donnée par la partie
imaginaire (respectivement réelle) de la fonction complexe :
On définit l’amplitude complexe de u = u (t) :
U = UMaxe jϕ0,u (c’est un nombre complexe)

8. Attention ! Le module de U, noté |U|, est ici égal à UMax (valeur maximale) ;
et non à UEff (valeur efficace) comme cela est parfois le cas lorsque le
coefficient √ 2 est arbitrairement introduit.
Remarque : Dans le cas d’un système linéaire où toutes les sources sont
synchrones (même temps) et de même fréquence, on peut faire abstraction
du terme exp (jωt), ce qui revient à travailler avec les seules amplitudes
complexes.
Méthode :
À chaque grandeur sinusoïdale on associe un nombre complexe, et
réciproquement

9. Question : Reprendre l’exemple précédent en utilisant la
méthode des complexes.
Réponse :
– À chaque courant, on associe un nombre complexe :
– Loi des nœuds :
D’où :

10. IMPÉDANCE ET ADMITTANCE
COMPLEXES D’UN DIPÔLE

11. Soit le dipôle linéaire ci- contre. La convention récepteur est adoptée.
• Définitions
L’impédance complexe Z d’un dipôle est le rapport de u (t) par i (t).
Avec :
ϕ = ϕ0,u − ϕ0,i ; R = Re (Z) = |Z| cos (ϕ) : résistance et X = Im (Z) = |Z| sin (ϕ) : réactance.
|Z|, R et X s’expriment en ohms (Ω).
L’admittance complexe Y est l’inverse de l’impédance complexe :
où G = Re (Y) = R/(R2 + X2) : conductance, B = Im (Y) = −X/(R2 + X2) : susceptance.
|Y|, G et B s’expriment en siemens (S) ou en ohms-1 (Ω-1).

12. • Schéma électrique et notations complexes
• Dipôles linéaires élémentaires

13. PUISSANCES – FACTEUR DE PUISSANCE

14. • Formules et relations
Amplitudes complexes : U = UMax e jϕ0,u et I = IMax e jϕ0,i
Déphasage de u par rapport à i : ϕ = ϕ0,u − ϕ0,i
Remarque :

15. • Puissances de dipôles linéaires élémentaires
• Facteur de puissance. Caractérise le taux d’utilisation du réseau.

16. • Interprétation physique
À la puissance active correspond une énergie active qui est absorbée et
transformée dans le récepteur en énergie thermique, mécanique, chimique, etc.
Par contre, à la puissance réactive correspond une énergie réactive qui va
périodiquement de la source vers le récepteur puis du récepteur vers la source,
et ainsi de suite sans ne jamais être absorbée par le récepteur.
L’existence d’une puissance réactive conduit à une augmentation du courant
dans le générateur et la ligne alimentant le récepteur. Cette augmentation
engendre un surcroît de pertes et nécessite un surdimensionnement des
moyens de transport. La puissance apparente est un élément de
dimensionnement de la ligne et du générateur.
Pour une puissance active donnée, plus le facteur de puissance est faible et plus
le courant est élevé. C’est pourquoi l’ONE impose un facteur de puissance élevé
et pénalise financièrement les consommateurs d’énergie réactive.

17. • Théorème de Boucherot.
La puissance active totale (respectivement réactive totale) consommée par
un ensemble de récepteurs est égale à la somme des puissances actives
(respectivement réactives) consommées par chaque récepteur.
Ainsi, une installation comportant n récepteurs, alimentée sous une tension
UEff et consommant un courant IEff, absorbe une puissance active PTot et une
puissance réactive QTot avec un facteur de puissance fP = cos (ϕ) tels que :
Attention ! Les puissances apparentes ne s’additionnent pas.
• Relèvement du facteur de puissance.
S ’il est inférieur à la norme, le facteur de puissance d’une installation doit être
relevé. Une méthode simple consiste à brancher en parallèle des condensateurs
sur l’installation généralement inductive.