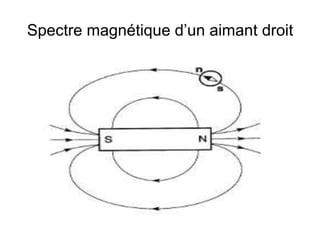
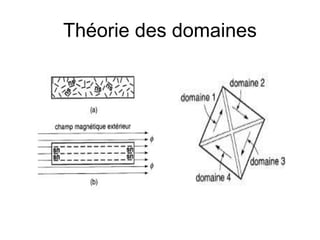
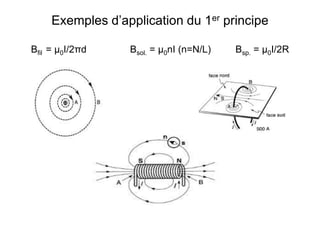
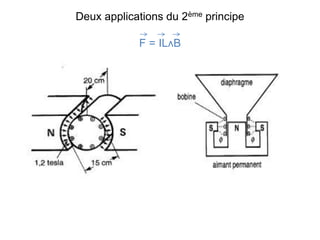
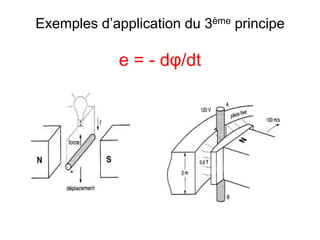
Le document traite des principes fondamentaux du magnétisme et de l'électromagnétisme, expliquant les propriétés des aimants, la création de champs magnétiques par des courants, et les forces électromagnétiques. Il décrit également les applications de la loi de l'induction électromagnétique de Faraday et le théorème d'Ampère, qui simplifient les calculs des champs magnétiques dans des circuits. Enfin, il illustre plusieurs principes avec des exemples concrets d'applications, tels que les moteurs électriques et les génératrices.

1. CHAPITRE 1
MAGNETISME

2. 1- RAPPELS
FONDAMENTAUX

3.  Les aimants existent à l’état
naturel mais on peut aussi
communiquer cette propriété de
magnétisme à certains corps
composés essentiellement de Fer,
Nickel, Cobalt … qu’on appelle
aimants artificiels.

4.  Un aimant est constitué d’un
pôle Nord et un pôle Sud.
Deux pôles de types contraires
(N-S) s’attirent alors que deux
pôles de même type (N-N ou S-S)
se repoussent.

5.  Dans l’espace entourant les pôles
d’un aimant existe un champ
magnétique composé de lignes de flux
ou lignes de force.
Les lignes de force forment des
boucles qui partent du pôle Nord et
entrent dans le pôle Sud.
L’ensemble de ces lignes constituent :
le spectre magnétique

6.  La somme des lignes de force
traversant une surface donnée
constitue le flux magnétique.
L’unité SI du flux est le Weber (Wb).
La densité du flux magnétique en un
point donné mesure l’intensité du
champ magnétique en ce point.
L’unité du champ est le Tesla (T) :
1T = 1Wb /m2.

7.  Certains matériaux ferromagnétiques
comme le Fer doux sont perméables
aux lignes de flux.
Cette propriété de canaliser les lignes
de champ s’explique par la théorie des
domaines : Chaque domaine constitue
un petit aimant s’orientant dans le sens
des lignes de force créées par le
champ extérieur et augmente ainsi la
densité du flux à l’intérieur du corps
ferromagnétique.

8.  Si on supprime le champ extérieur,
le corps ferromagnétique conserve
une certaine aimantation
rémanente ou champ rémanent :
c’est ce qui distingue les aimants
permanents.

9. Spectre magnétique d’un aimant droit

10. Flux magnétique

11. Théorie des domaines

12. 2- PRINCIPES
DE
L’ELECROMAGNETISME

13. 1er Principe :
création d’un champ
par un courant

14. Tout conducteur parcouru
par un courant s’entoure
d’un champ magnétique.
Les lignes de force suivent
des cercles concentriques
autour du conducteur.

15. Pour un courant donné, l’intensité
du champ magnétique à une
distance donnée du centre du fil
peut être calculée par une
formule simple : (loi de Biot et Savart)

16. De la même façon, une spire et plus
généralement une bobine parcourue par un
courant, est traversée par un flux magnétique
dont les lignes de force sortent par une
extrémité constituant le pôle Nord et rentrent
par l’autre extrémité constituant le pôle Sud.
Le produit NI (nombre de spire x courant) est
appelé : la force magnétomotrice développée
par la bobine.
Une bobine parcourue par un courant produit
donc un champ magnétique tout comme un
aimant permanent.

17. Cette propriété est mise à profit dans les
électro-aimants constitués d’une bobine
enroulée autour d’un noyau de fer doux.
Sa perméabilité élevée permet d’amplifier
des milliers de fois le champ magnétique
créé par la bobine.
On les retrouve dans les pôles des
machines électriques, les disjoncteurs, les
relais et les sonneries.

18. Exemples d’application du 1er principe
Bfil = μ0I/2πd Bsol. = μ0nI (n=N/L) Bsp. = μ0I/2R

19. 2ème Principe :
forces
électromagnétiques

20. Un conducteur parcouru par un
courant et placé dans un champ
magnétique est soumis à une force
électromagnétique : cette force, qui
peut être calculée par une formule
simple, dépend du courant, de
l’intensité du champ, de la longueur
et de l’orientation du conducteur par
rapport aux lignes de champ.
(force de Laplace)dF = I dl Ʌ B

21. Comme un conducteur parcouru
par un courant crée aussi son
propre champ magnétique, il en
découle que des conducteurs
voisins sont soumis à des forces
d’attraction ou de répulsion qui
dépendent des sens des
courants.

22. Ces forces électromagnétiques
trouvent de nombreuses applications
dont la plus importante en
électrotechnique est le moteur
électrique.
Elles peuvent aussi avoir tendance à
déformer des circuits parcourus par
des courants intenses (Exemple :
haut parleur électromagnétique).

23. Deux applications du 2ème principe
F = ILᴧB

24. 3ème principe :
tension induite dans
un conducteur

25. C’est la loi de l’induction
électromagnétique de Faraday. Selon
ce principe une tension est induite dans
un conducteur en mouvement dans un
champ magnétique ou plus
généralement, lorsque le conducteur
« coupe » les lignes de champ.
Cette tension dépend seulement du
taux de changement ΔØ/Δt du flux
balayé par le conducteur.

26. La loi de l’induction de Faraday
est à l’origine des machines
tournantes générant de
l’électricité :
- Génératrices à courant continu,
- Alternateurs générant une
tension alternative.

27. Exemples d’application du 3ème principe
e = - dφ/dt

28. 4ème Principe :
l’utilisation de la loi
précédente dans sa
forme la plus générale

29. Une tension est induite à
l’intérieur d’une boucle par un
flux qui varie avec le temps.
Cette tension est proportionnelle
au taux de variation ΔØ/Δt du
flux dans la boucle.
Pour une bobine la tension est
multipliée par le nombre de
spires.

30. La loi de Lenz permet de trouver la
polarité de la tension induite.
D’après cette loi, la polarité est telle
qu’un courant imaginaire sortant de
la borne + de la boucle (ou de la
bobine) crée un flux qui s’oppose à
la variation du flux imposé.
Cette loi s’applique même si la
boucle porte déjà un courant.

31. Exemple d’application
Une bobine comprenant 2000 spires est
traversée par un flux de 5 mWb provenant
d’un aimant permanent. L’aimant est
ensuite éloigné de la bobine en 1/10 de
seconde et le flux à l’intérieure de la
bobine baisse à 2 mWb.
Quelle est la valeur moyenne de la f.e.m.
induite E ?
Quelle est sa polarité ?

32. 3. THEOREME
D’AMPERE

33. Considérons un contour fermé (C) orienté. Le sens de la normale n à la
surface qui s’appuie sur le contour est donné par la règle de la main
droite :
Par définition, la circulation C du champ magnétique B le long du
contour fermé (C) est : C = Σ(C) B.dℓ = ∫(C) B.dℓ
Théorème d’Ampère :
La circulation du champ magnétique le long d’un contour fermé est égale
à la somme des intensités algébriques des courants enlacés, multipliée
par μ0 : C = μ0 Σj Ij les courants étant comptés positivement s’ils ont même
sens que la normale n.
En toute rigueur, le théorème d’Ampère n’est valable que dans le vide. On
peut cependant l’appliquer dans l’air.
Pour la figure ci-dessus : C = μ0 Σj Ij = μ0 (– I1 – I2 + I3)

34. Application :
Dans les circuits filiformes possédant des symétries géométriques, le
théorème d’Ampère permet de calculer très rapidement l’intensité du
champ magnétique (à condition de choisir judicieusement le contour
fermé …).
Par exemple, reprenons le conducteur rectiligne infiniment long :
On choisit un contour fermé s’appuyant sur une ligne de champ.
La circulation du champ magnétique B le long du contour fermé est
donc :
Appliquons le théorème d’Ampère :
Il est clair que les calculs sont beaucoup plus simples qu’avec la
formule de Biot et Savart …