Le document traite des concepts de magnétisme et d'induction, y compris les champs magnétique et d'induction, les lois de l'induction et d'ampère, ainsi que les propriétés des matériaux en termes de perméabilité magnétique. Il explore également des applications telles que les circuits magnétiques et l'énergie emmagasinée dans les champs électriques et magnétiques. Enfin, il aborde les forces magnétiques et les systèmes de contrôle électronique associés à la régulation du courant.

1. Magnétisme et induction
Dominic Grenier
Design III
A-09

2. 2www.ulaval.ca
•B = champ d'induction magnétique [Tesla : T]
ou densité de flux magnétique [Wb/m2 = T]
•H = champ magnétique [A/m]
(par analogie avec le champ électrique E [V/m])
B = μ H
• μ = perméabilité [H/m] = μrμ0
•perméabilité du vide μ0=4 *10-7 H/m
•produit par un courant i.e. déplacement de charges électriques
(champ E produit par des charges électriques)
Champ d'induction magnétique

3. 3www.ulaval.ca
Perméabilités de matériaux
Matériau Perméabilité [H/m] Perméabilité relative / 0
.
Eau 1.2566270 10-6 0.999992
Cuivre 1.2566290 10-6 0.999994
Vide 1.2566371 10-6 ( 0) 1
Hydrogène 1.2566371 10-6 1.0000000
Aluminium 1.2566650 10-6 1.000022
Platine 1.2569701 x10-6 1.000265
Nickel 125 10-6 100-600
ferrite (nickel zinc) 20-800 10-6 16-640
ferrite (manganèse zinc) >800 10-6 >640
Acier 875 10-6 700
Acier électrique 5000 10-6 4000
Permalloy 10,000 10-6 8000
Mu-metal 25,000 10-6 20,000
(source : wikipédia)

4. 4www.ulaval.ca
Champ d'induction par un fil infini
Fil infini parcouru par un courant I
•Règle de la main droite
•Ligne de champ qui boucle sur elle-même
B =
μI
2 r
a

5. 5www.ulaval.ca
Loi de l'induction
Première équation de Maxwell dite équation de Faraday
f.e.m.= Eidl
=
d
dt
Bids
S
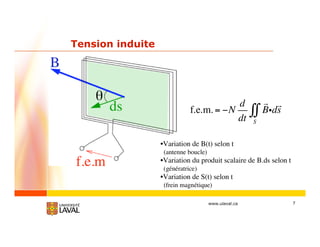
•f.e.m. = force électromotrice [V]
Équivalent à une tension en quasi-statique i.e. basse-fréquence
•S est délimitée par le parcours fermé l
•ds pointe dans la direction exprimée par la règle de la main droite
= flux magnétique [Wb]

6. 6www.ulaval.ca
Cas de N boucles
f.e.m.= N
d
dt
1
1=flux intercepté par une seule boucle de fil

7. 7www.ulaval.ca
Tension induite
f.e.m.= N
d
dt
Bids
S
•Variation de B(t) selon t
(antenne boucle)
•Variation du produit scalaire de B.ds selon t
(génératrice)
•Variation de S(t) selon t
(frein magnétique)

8. 8www.ulaval.ca
Inductance
Inductance :
(auto-inductance externe)
(self en bon français :-)
L =
I
Boucles en solénoïde : L = N 1
I
μN2
A
h

9. 9www.ulaval.ca
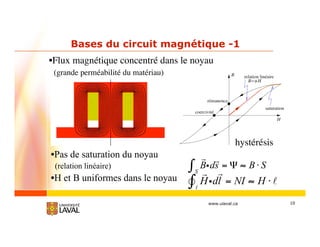
Loi d'Ampère
Hidl =[I]s
+
t
Dids
S
assumé faible devant [I]s en quasi-statique
Cas de N boucles de fil sur lequel circule un courant I
Hidl = NI
Seconde équation de Maxwell dite équation d'Ampère

10. 10www.ulaval.ca
Bases du circuit magnétique -1
•Flux magnétique concentré dans le noyau
(grande perméabilité du matériau)
Hidl = NI H
•Pas de saturation du noyau
(relation linéaire)
•H et B uniformes dans le noyau
BidsS
= B S
hystérésis

11. 11www.ulaval.ca
Bases du circuit magnétique -2
•Loi d'Ampère et conservation de flux
•Analogie avec la relation d'Ohm
NI = H =
B
μ
= B S
NI =
B
μ
=
μS
V = RI
R

12. 12www.ulaval.ca
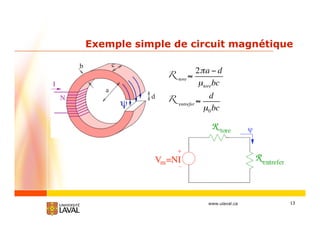
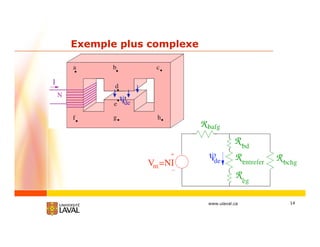
Réluctance
•symbole : R [H-1]
•équivalences Circuit magnétique
R
NI [A·tours]
Circuit électrique
• R
• V
• I
•élément de volume :
(bloc)

13. 13www.ulaval.ca
Exemple simple de circuit magnétique
tore
2 a d
μtorebc
entrefer
d
μ0bc
R
R

14. 14www.ulaval.ca
Exemple plus complexe

15. 15www.ulaval.ca
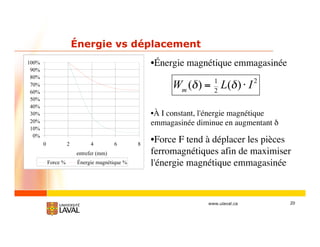
Énergie emmagasinée
• énergie électrique
emmagasinée dans un champ électrique E
(dans un condensateur par exemple)
• énergie magnétique
emmagasinée dans un champ magnétique H ou B
(dans une inductance par exemple)
We
=
1
2
CVab
2
=
1
2
E2
dv
V
densité d'énergie électrique [J/m3]
Wm
=
1
2
LI0
2
=
1
2
BH dv =
1
2
B2
μVV
dv
densité d'énergie magnétique [J/m3]
Eidl =Vab
a
b
Hidl = I0

16. 16www.ulaval.ca
Exemple simple d'énergie magnétique
Wm
=
1
2
Btore
2
μtoreVtore
dv +
1
2
Bentrefer
2
μ0Ventrefer
dv
=
1
2
B2
μtore
dv
Ad
2 a
+
1
2
B2
μ0
dv
A0
d
=
1
2
B2
A
2 a d
μtore
+
d
μ0
=
1
2
2
A
2 a d
μtore
+
d
μ0
=
1
2
(R
tore
+R
entrefer
) 2
A = bc
BA
Wm
=
1
2
(NI)2
R
tore
+R
entrefer

17. 17www.ulaval.ca
Force magnétique
Force agissant sur chaque charge qui se déplace dans un champ magnétique
•composante perpendiculaire au déplacement (courant) de B
•règle de la main droite
F = qv B
= I dl B

18. 18www.ulaval.ca
Force développée par un aimant
Calcul à partir de la variation d'énergie magnétique emmagasinée
•considérer de l'épaisseur d de la pièce dans le calcul de sa réluctance
•supposer un entrefer (ou sur la figure de 2 entrefers) de dimension non-nulle
•déterminer la variation de l'énergie magnétique emmagasinée selon la variation de
•faire tendre vers quelque chose de petit
(la rugosité du noyau, de la pièce, et autres éléments susceptibles d'empêcher un contact franc)
F = W F =
dWm
d
entrefer1
= entrefer2
=

19. 19www.ulaval.ca
Flux déformable avec entrefer
entrefer

20. 20www.ulaval.ca
Énergie vs déplacement
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
0 2 4 6 8
entrefer (mm)
Force % Énergie magnétique %
•Énergie magnétique emmagasinée
•À I constant, l'énergie magnétique
emmagasinée diminue en augmentant
•Force F tend à déplacer les pièces
ferromagnétiques afin de maximiser
l'énergie magnétique emmagasinée
Wm
( ) = 1
2
L( ) I2

21. 21www.ulaval.ca
Électronique de contrôle
Régulateur :
•Nécessaire au maintient d'une force constante et donc d'un courant I moyen
constant malgré la décharge de la capacité (qui contient l'énergie sous forme
électrique)
•Optimisation de la consommation de l'énergie
•Suggestion : régulation par hystérésis
•lecture du courant
(e.g. au travers une petite résistance en série avec la bobine,
avec amplificateur d'instrumentation)
•rétroaction en tension pour réguler le courant par différence de potentiel
•utilisation d'un MOSFET de puissance et d'une diode zener
ajustement d'un rapport cyclique pour modifier le I moyen