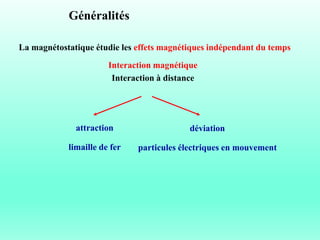
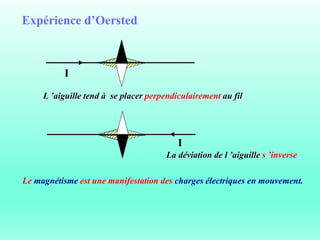
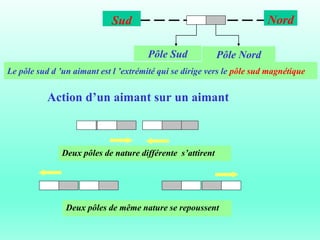
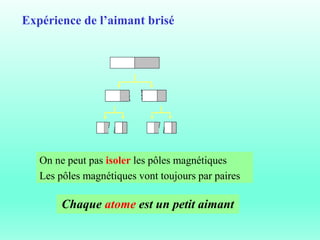
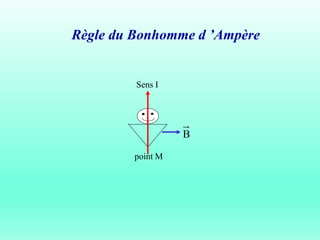
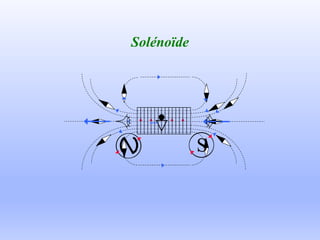
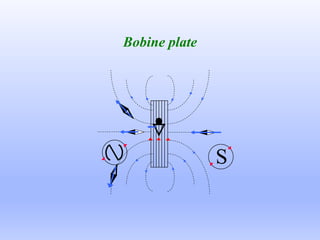
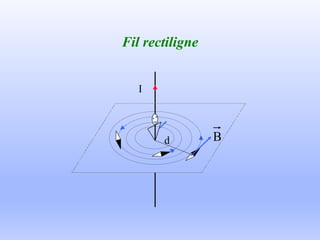
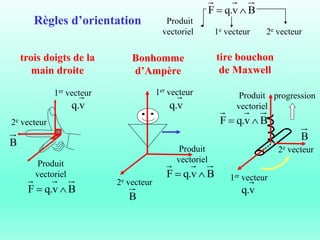
Le document traite du ferromagnétisme et de la magnétostatique, examinant les interactions magnétiques et les effets des champs magnétiques créés par des électrons en mouvement. Il décrit les différentes sources magnétiques, les concepts de force de Lorentz et de champ magnétique, ainsi que les lois de Biot et Savart. Les expériences historiques, comme celle d'Oersted, illustrent le lien entre l'électricité et le magnétisme.