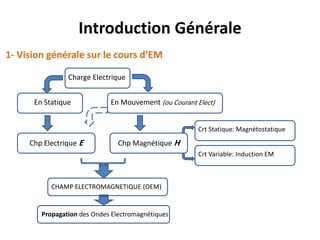
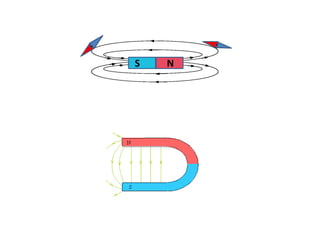
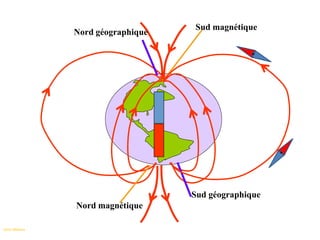
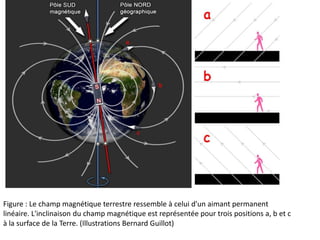
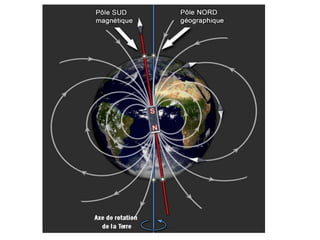
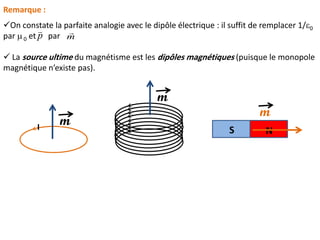
Ce document présente une introduction à l'électromagnétisme, explorant des concepts tels que la magnétostatique, l'induction électromagnétique et les équations de Maxwell. Il explique les sources de champ magnétique, notamment les aimants, la Terre, et les circuits électriques, tout en détaillant les propriétés des champs magnétiques statiques. Enfin, il aborde des propriétés mathématiques et théorétiques, ainsi que la force de Lorentz et le théorème d'Ampère en magnétostatique.

1. ELECTROMAGNETISME
Introduction Générale
Chap. I : Magnétostatique
Chap. II : Induction électromagnétique
Chap. III : Equations de Maxwell
Chap. IV: Propagation des OEM dans le vide

2. Charge Electrique
Introduction Générale
En Statique En Mouvement (ou Courant Elect)
Chp Electrique E Chp Magnétique H
Crt Statique: Magnétostatique
Crt Variable: Induction EM
CHAMP ELECTROMAGNETIQUE (OEM)
Propagation des Ondes Electromagnétiques
1- Vision générale sur le cours d’EM

3. 2-Electrostatique (Rappel)
 Déterminer le champ E à partir des sources:
• Une charge ponctuelle,
• Plusieurs charges ponctuelles,
• Une répartition de charges (distribution linéique, surfacique ou volumique).
 Les relations de bases:
0
int
.

 S
S
Q
SdE  

0

Ediv

VgradE 
 etc…….
3- Opérateurs & Outils mathématiques
 Le Gradient: ffgrad 
• Mesure la non uniformité d’un champ de scalaire,
• Indique les valeurs croissantes d’un champ de scalaire,
 La Divergence: AAdiv

.
• Un champ divergent (convergent) a une divergence positive (négative),
• Le champ uniforme et le champ à caractère tourbillonnaire ont une
divergence nulle,

4.  Le Rotationnel: AArot


A

0

Arot• traduit le caractère tourbillonnaire du champ vectoriel
Les lignes de champ sont fermées, et tournent autour du rotationnel dans le
sens positif.
dAdivSdA
VS   

.Théorème de la divergence
 
surappyuants'S..
S
SdArotdA



Théorème du rotationnel
 0)(  BdivArotB

BrotAArotBBAdiv

..)( 
0)( Arotdiv

 le flux de est conservatif.A

00.   AdivSdA
S


0

 ArotVgradA
0)(

Ugradrot
AGgradArotGAGrot

)(
AAdivgradArotrot
 2
)()( 

5. Chap. I : La magnétostatique
1- Introduction
• Des siècles avant notre ère, il a été constaté que quelques pierres (magnétite
Fe3O4) ont un comportement gravitationnel sans rapport ni avec la gravitation ni
avec les phénomènes électriques. Ce phénomène est appelé magnétisme relatif à
la région « magnésie » de l’Asie mineure où a été constaté, pour la première fois, ce
phénomène.
• Les chinois furent les premiers à utiliser les propriétés des aimants, il y a plus de
1000 ans, pour faire des boussoles.
• Il fallait attendre la fin du XIXème siècle pour qu’une théorie complète apparaisse;
la théorie de l’électromagnétisme où l’électricité et le magnétisme sont deux
aspects d’un même phénomène.

6. • Tout commence avec l’expérience du physicien Oersted (1819) qui constate
que le passage d’un courant électrique le long d’un fil fait dévier l’aiguille d’une
boussole, ce qui prouve l’existence de forces magnétiques dues aux courants
électriques.
• L’étude quantitative des interactions entre aimants et courants fut faite par les
physiciens Biot et Savart (1820).
• Un grand nombre physiciens célèbres a contribué à l’élaboration de la théorie
électromagnétique: Oersted, Ampère, Faraday, Foucault, Henry, Lenz, Maxwell,
Weber, Helmholtz, Hertz, Lorentz ...
• Si la théorie d’électromagnétisme débuta en 1819 avec Oersted, elle ne fut mise
en équations par Maxwell qu’en 1873 et ne trouva d’explication satisfaisante,
dans le cadre de la théorie de la relativité d’Einstein, qu’en 1905.
Nous nous intéressons ici à La magnétostatique qui consiste à étudier les
champs magnétiques stationnaires (indépendants du temps).

7. 2- Sources de champ magnétique
2-1- Aimants
L'approche d'une aiguille aimantée (boussole) vers un aimant droit donne les
résultats suivants :
- L'aiguille change de sens suivant l'extrémité de l'aimant qu'elle approche.
- Le pôle nord de l'aiguille est attiré par le pôle sud de l'aimant.
On peut donc en déduire les propriétés suivantes :
• Un aimant possède un pôle nord et un pôle sud, qui sont indissociables.
• Contrairement à l’électrostatique , on ne peut isoler et manipuler
indépendamment des entités qui seraient de type nord et de type sud.
NS
• Les pôles opposés s'attirent et les pôles semblables se repoussent.
• L'aiguille aimantée est un aimant à deux pôles.

8. 2-2- planète Terre
La boussole s'oriente dans une direction et un sens précis sans l'influence d'un
aimant proche. Le pôle nord de l'aiguille indique le pôle Nord géographique.
On en déduit que :
• La planète Terre est une source de champ magnétique.
• Le pôle Nord géographique est en fait , à peu près, le pôle sud magnétique.
2-3- Circuits parcourus par des courants
Approchons l'aiguille aimantée d'un circuit électrique.
• En l'absence de courant dans le circuit, l'aiguille indique le Nord géographique.
•En présence d'un courant dans le circuit, l'aiguille s'oriente dans une autre position
stable et cette position s'inverse si on change le sens du courant dans le circuit.
On en déduit les propriétés suivantes :
• Tout circuit élect. parcouru par un courant est une source de champ magnétique.
• Le sens du chp magnétique peut être inversé en changeant le sens du courant.

9. 3- Champ (ou induction) magnétique statique dans le vide
Par analogie avec les interactions électriques et gravitationnelles, on peut donc
dire qu’un aimant (ou courant électrique) crée dans son voisinage un champ
magnétique tq , où est l’induction magnétique et est la
perméabilité magnétique du vide dont la valeur numérique est SI
Au sein d’un matériau magnétique , l’ind. Mag. est donnée par:
où est la perméabilité relative du milieurHHB r

  0
HB

0 0
7
0 104 
 
H

B

L'intensité du chp mag. peut se mesurer directement avec un teslamètre (voir TP).
La direction des lignes de champs peut être déterminer à l’aide d’une boussole.
On peut retenir que:
•Les lignes de champ magnétique se dirigent du pôle nord vers le pôle sud.
•Elles sont resserrées dans les régions où le champ est intense.
3-1- Lignes de champ des aimants et de la terre

10. S N

11. Sud magnétique
Nord magnétique
Nord géographique
Sud géographique
1ere Séance

12. Figure : Le champ magnétique terrestre ressemble à celui d'un aimant permanent
linéaire. L'inclinaison du champ magnétique est représentée pour trois positions a, b et c
à la surface de la Terre. (Illustrations Bernard Guillot)

14. 3-2- Unité et ordre de grandeurs :
 B se mesure en tesla ou en Gauss 1 tesla=104 Gauss,
 L’induction magnétique terrestre vaut 0,5 Gauss à Paris,
 Un aimant de qualité courante donne 10 Gauss (10-3 tesla). Un très bon aimant
peut atteindre quelques centaines de Gauss,
 Un électroaimant ordinaire peut atteindre le tesla,
 Des gros électroaimants avec des bobines supraconductrices (moyens très
onéreux) parviennent à 20 teslas.
3-3- Induction magnétique créée par une charge en mouvement
On considère une particule de charge q animé d’une vitesse se trouvant au point P à
l’instant t, l’ind. Mag. crée par cette charge en un point M quelconque est exprimée
par :
v

PMr
r
rv
q
PM
PMv
qMBMBP 






posanten,
44
)()( 3
0
3
0




MP
q
v

B


15. 3-4- Induction magnétique créée par un ensemble de charges en mouvement
Pour un ensemble de N charges en mouvement l’induction mag. est donnée par:
MPr
r
rv
qMB ii
N
i i
ii
i 

 


posanten,
4
)(
1
3
0


3-5- Induction magnétique créée par un élément de volume
Pour un élément de volume d , de charge dQ et animé d’une vitesse ( ), l’induction
mag. est donnée par:
3
0
4
)(
r
rv
dQMBd
 


 MP
dQ
v

Bd

d

16. Dans le cas d’un circuit filiforme (les dimension
transversales des fils sont négligeables), on démontre que :
3
0
4
)(
r
rd
IMBd



 



a) Courants filiformes


d
I
P
S
3-6- Induction magnétique créée par des distributions de courant
L’induction mag. créée par une portion infiniment
petite de ce fil est alors donnée par :
dQvdI .. 
(Loi de Biot et Savart)



)(
3
0
4
)(
C
r
rd
IMB





En intégrant sur la totalité du circuit, on obtient :
Le sens de l’induction mag. est déterminé par la règle du tire-bouchon de Maxwell
ou la règle du bonhomme d’Ampère

17. En intégrant sur tout le volume, on obtient :
  PMravec
4
)( 3
0


 



volume
d
r
rPj
MB 


b) Courants volumiques
3
0
4
)(
r
rd
dIMBd

 



j

P
PdSd
Considérons un tube élémentaire de courant (dl , dS) centré au point P et parcouru
par une densité de courant .J
L’induction mag. Créée par ce tube de courant est donnée par:



d
r
rJ
MBd 3
0
4
)(
 

2eme Séance

18. Exemple :
Calculons l’induction magnétique crée par un fil fini parcouru
par un courant d’intensité I.



eMB

I
2
)( 0

c) Courants surfaciques
Dans le cas d’une nappe de courant parcourue par une densité de courant
surfacique sJ
dS
r
rJ
MB
S
S


 3
0
4
)(



H M
I
 )(MB

)(Pd

P 2
1



eMB

)sinI(sin
4
.....)( 12
0

Dans le cas d’un fil infini

19. Un vecteur polaire, ou vrai vecteur, est un vecteur dont la direction, le module et
le sens sont parfaitement déterminés.
Exemples : vitesse d’une particule, champ électrostatique, densité de
courant.
En Physique, on distingue 2 types de vecteurs:
Un vecteur axial, ou pseudo-vecteur, est un vecteur dont le sens est défini à partir
d’une convention d’orientation d’espace et dépend donc de cette convention.
Exemples : Le produit vectoriel, le champ magnétique, la normale à une
surface.
4-1- Vecteurs et pseudo-vecteurs
4- Propriétés de symétrie de l’induction magnétique
L’exploitation des symétries permet de simplifier considérablement le calcul de
l’induction magnétique. Les propriétés de symétrie sont donc fondamentales .

20. 4-2- Comportement vis-à-vis des plans de symétrie et d’antisymétrie
Il est à noter qu’en tout point d’un plan de symétrie  ,
Un vrai vecteur (E par exemple) est contenu dans le plan de symétrie;
Un pseudo-vecteur (B par exemple) est perpendiculaire au plan de symétrie.
Cas d’un système possédant un plan de symétrie
Il est à noter qu’en tout point d’un plan d’antisymétrie ’ ,
Un vrai vecteur (E par exemple) est perpendiculaire au plan d’antisymétrie;
Un pseudo-vecteur (B par exemple) est contenu dans le plan d’antisymétrie.
Cas d’un système possédant un plan d’antisymétrie

21. B est perpendiculaire au plan de symétrie en tout point de celui-ci,
Cas d’un plan de symétrie
Lorsqu’une distribution présente 2 plans de symétrie, l’intersection de ces plans est
un axe de symétrie. B est alors nul en tout point de cet axe de symétrie,
Cas d’un axe de symétrie
Lorsqu’une distribution présente plusieurs plans de symétrie qui se coupent en un
point donné, on parle de centre de symétrie, B est alors nul en ce point,
Cas d’un centre de symétrie
B est contenu dans le plan d’antisymétrie.Cas d’un plan d’antisymétrie
B est porté par l’axe de symétrieCas d’un axe d’antisymétrie
Cas d’un centre d’antisymétrie B est nul au centre d’antisymétrie.
A partir de ces propriétés, nous pouvons déduire ce qui suit:

22. 5- Actions électrodynamiques
Si en plus le champ électrique est non nul, la force totale
est donnée par : )( BvEqF


Cette force est appelée force de Lorentz.
5-1- Force exercée sur une particule chargée
Dans une région où règne une induction magnétique ,
une particule de charge q animée d’une vitesse subie
une force magnétique exprimée par:
v

B

BvqF


5-2- Force exercée sur un élément de courant (Force de Laplace)
b) Courants volumiques )()()()( MdMBMJMFd 


c) Courants surfaciques )()()()( MdSMBMJMFd S


Ces formules
expriment la loi de
Laplace.
Exemple:
Déterminer la force par unité de longueur mise en jeu dans le cas deux fils
conducteurs infinis, distants de a et parcourus dans le même sens par les
courants I1 et I2 .
Reprenons le même raisonnement du § 3-6
)()()( MBMIdMFd



a) Courants filiformes
a
I2
I1

23. 6-Théorème d’Ampère
En électrostatique, on a utilisé le théorème de Gauss pour déterminer le champ
électrostatique dans le cas des configurations à fortes symétries.
En magnétostatique, il existe un théorème relatif à l’induction magnétique connu
par le théorème d’Ampère.
I1
I2 I3 I4
I5
()
Dans le cas d’une distribution quelconque de courants, la circulation de l’ind. Mag. B le
long du contour fermé () orienté est donnée par l’expression:
 

)(
00
)(
..
Si
i dSJIdB 

(Théorème d’Ampère)
(S) est une surface qui s’appuie
sur le contour ()

24. )(. 310 IIdB 

 
I
IdB 02. 



I1
I2
I3
I4
Remarque :
 

i
iIdH 

. , H s’exprime donc en A/m.
7- Equations locales de B

Soit (S) une surface quelconque s’appuyant sur le contour ():
.. 0  
 S
SdjdB



 ..,  
 S
SdBrotdBor



On en déduit qu’en chaque point, l’ind. Mag vérifie la relation : jBrot

0
7-1 Théorème d’Ampère
Cette équation exprime la formulation locale du théorème d’Ampère
Fil infini parcouru par un courant d’intensité I 
I
’

Exemple:
B


25. Appliquons maintenant la divergence à l’équation précédente :
 0)( 0 jdivBrotdiv

 0jdiv

la loi de conservation de la
charge en magnétostatique
7-2- Conservation du flux de B

Calculons la divergence (par rapport à M) de l’expression générale de l’ind. Mag.
   





volumevolume
d
r
rPj
divd
PM
PMPj
divMBdiv 





)(
4
)
4
()( 3
0
3
0


Tenons compte des 2 propriétés suivantes :
et)
1
( 3
r
r
r
grad

 BrotAArotBBAdiv

..)( 
r
gradrotPjPjrot
r
r
r
r
Pjdiv
1
).()(.))(( 33



Or, et0
1 

r
gradrot r)depasdépendne)((car0)( PjPjrot


On trouve finalement : 0Bdiv


26. 8- Potentiel vecteur
8-1 Définition
Si en électrostatique le champ électrostatique dérive d’un potentiel scalaire, en
magnétostatique l’induction magnétique dérive aussi d’un potentiel mais de nature
vectoriel.
La divergence d’un rationnel étant toujours nul, il existe donc un champ de vecteur
tel que :
A

ArotB

 est appelé potentiel vecteurA

Invariance et choix de jauge
Puisque le rationnel d’un gradient est nul, le potentiel vecteur n’est déterminé qu’à un
gradient près:
La forme intégrale s’en déduit en utilisant le théorème d’Ostrogradski:


dBdivdSB
S
..  

On déduit donc que l’ind. Mag. est un champ de vecteur à flux conservatif.
0.  S
dSB
Remarque: L’induction magnétique s’exprime aussi en Weber/m2

27. On lui impose une condition supplémentaire (condition de jauge) pour en sélectionner
une configuration physiquement acceptable. On parle alors d’un choix de jauge.
0Adiv










0
0
AAdivgradArotrot
jBrot



8-2- Equations locales de A

Partons des relations suivantes:
jA

0 Équation de
Poisson
Cette équation est analogue à l’équation de Poisson
à la quelle satisfait le potentiel scalaire V :
0

V
La jauge utilisée dans le cas statique est la jauge
de Coulomb dont l’expression est:
fgradAAA 



' est appelée invariance de Jauge.La transformation
BfgradrotArotArotB




0
''
' fgradAAetArotB 

Si
alors
3 eme Séance

28. Par analogie avec l’expression du potentiel scalaire: , 


d
r
P
MV
volume
)(
4
1
)(
0
l’expression du potentiel vecteur est donnée par : 


d
r
Pj
MA
volume
)(
4
)( 0


Dans le cas des distributions linéiques de courant:






IdSjdSdjdj  
fil r
dI
MA





4
)( 0
8-3- Equation intégrale de A

Calculons le flux de l’induction magnétique à travers une surface (S) quelconque
s’appuyant sur un contour  :
..  
 

dASdB
S
On pourrait donc utiliser cette équation intégrale pour déterminer l’expression du
potentiel vecteur.
..  
SS
SdArotSdB



29. 1
2
a) Considérons un petit cylindre caractérisé par: dS et dh
Et puisque le flux à travers la surface latérale s’annule lorsque dh0:
0.B.B 121n122n  dSndSn

2n1n BB


La composante normale de l’induction mag. est continue
b) On considère le contour CDEF quelconque
udMN


),,( 12nuw

forment un trièdre direct
w

étant le vecteur unitaire normale à la boucle CDEF
S
C D
EF
K
 u

w

12n

M N
Soit une surface (S) parcourue par un courant de densité surfacique .sJ

9- Conditions aux limites entre 2 milieux
0.B
Cylindre
 dS
0... 12
1
112
2
2   dSnBdSnBdSnB
SlSbSb
2
1
12n

S
dS
dh
Lorsque dh=DE 0, on prend CD=MN=dl

30. Seules les composantes tangentielles de l’induction contribuent à la circulation




dwJd s ).().BB( 02t1t 
 1201t2t )BB( nJs

 
La composante tangentielle de l’induction subit une discontinuité à la traversée
d’une nappe de courant
Id 0
CDEF
.B  

).().BB( 021 



dwJd s
Appliquons le théorème d’Ampère:
 sJnudd



 1202t1t .).BB( 




dnuJd s ).().BB( 1202t1t  
  





dceci.).BB( 1202t1t  sJndd 
4 eme Séance

31. 





eBeB
e
r
e
r
MB
rr
r









 33
0 sin
cos
2
4
)()2
m
m
zeIRSI
 2
m
10- Dipôles magnétiques
Un milieu magnétique peut être considéré comme un ensemble de boucles de très
petites dimensions dont les effets sont étudiés à des distances macroscopiques.
De telles boucles sont appelées dipôles magnétiques.
Le moment magnétique est défini par
Dans le cas d’une spire parcourue par un courant d’intensité I (OM= r >> R).
On démontre que :
H
I
O y
x
z

H e

e

M

re

e
 
2
0
4
)()1
r
e
MA r
 

m


B

 m)3 Le moment du couple qui s’exerce sur le dipôle lorsqu’il est
dans un champ magnétique B

32. I
m
m
NS
m
On constate la parfaite analogie avec le dipôle électrique : il suffit de remplacer 1/0
par 0 et par
 La source ultime du magnétisme est les dipôles magnétiques (puisque le monopole
magnétique n’existe pas).
p

m

Remarque :

33. Lors d’un petit déplacement du circuit de , la force
magnétique effectue le travail ,
rd

rdBdIrdFdWd LAP



).(.2

rdFdWd LAP

.2

d = dc est appelé flux coupé (flux à travers la surface jaune)
Le travail de la force magnétique, entre deux positions initiale (1) et finale (2), est
donné par:
CoupéLAP IIW   )( 12
Considérons un circuit filiforme parcouru par un courant I, placé dans une ind.mag. B.
Un élément de longueur subi la force de Laplace :
11- Energie magnétostatique
a) Cas d’un courant filiforme plongé dans une induction magnétique
BIdFd






d
I
rd

B

C
Sd
2
Dans le cas d’un circuit rigide on peut montrer que: 12  Coupé
(Théorème de Maxwell)
dIdWLAP 
2
dIBdrdI
Sd





.)(
2

 SdBI
 2
.
 Travail des forces de Laplace

34. 0)( mWEt puisque pour un circuit placé à l’infini
IWm 
On en déduit que l’énergie mag. (potentielle) d’un circuit élect.
parcouru par un courant (I) et placé dans une ind. Mag est:
Donc: CsteIWm  
Considérons un circuit électrique parcouru par un courant permanent I et placé
dans un champ mag. statique.
Le circuit est donc soumis à la force de Laplace.
Il est susceptible de bouger et donc de développer une vitesse.
Appliquons le théorème de l’énergie cinétique ΔEc =WLAP = I.ΔΦ > 0
Le circuit possède donc une énergie potentielle liée à la présence du
champ mag.
Le mouvement se fait donc dans le sens qui accroit le flux traversant le
circuit: C’est la règle du flux maximal.
Appliquons la conservation de l’énergie totale du circuit:
E = Ec + Wm dWm = - dEc Wm = -  Ec = - I  = - I ( 2 -  1)
 Energie potentielle magnétique
4eme Séance

35.  Calcul des forces de Laplace à partir du flux
i
m
i
x
W
F



i
i i
m
m dx
x
W
dW  


3
1
gradIWgradF m 

Dans le cas de rotation, on démontre que le moment de la force magnétique par
rapport à un axe Δi passant par le centre d’inertie O du circuit, dépend de la
variation de flux lors d’une rotation du circuit autour de cet axe:
i
ii I




 /
Remarque
drFdWLAP .

 i
i
i dxF

3
1
On démontre que dans le cas de (n) circuits filiformes parcourus par des
courants I1, I2, …., In , l’énergie magnétostatique est donnée par:


n
i
iim IW
12
1


n
j
i ji
1
avec 
 Dans le cas d’un dipôle magnétique, on aura:
dIdWm  am BmW

.dSBI a.

 aBmd

.
b) Energie magnétique d’un système de circuits
5 eme Séance

36. c) Cas de distribution volumique de courants
Soit une distribution volumique de courants qui crée en tout point de l’espace une
induction magnétique B. On considère que cette distribution est constituée par un
ensemble de tubes de courants.
JdSdI  étant le courant d’un tube de
courant donné, de section dS.


ddS
dIdWm
2
1
  
tubeS
dASdB
tube


..

volume
m dAjW 

.
2
1
où
ce qui donne 

dVWe 
2
1

Tube
m dAdSJdW 

..
2
1


dAdSJWd m ..
2
12

Analogie avec l’électrostatique
 le flux traversant la surface qui délimite ce tube.
dAJ

.
2
1
dSdAJ ..
2
1




37. 0).(soit,
1
,
1
,rSPour 2
2
 SdBArS
r
B
r
A



espace
2
02
1
t
m dBW 

Enfin on aura :
On dit que l’énergie magnétique est localisée dans l’induction magnétique
c) Localisation de l’énergie magnétostatique

volume
m dAjW 

.
2
1
vrotuurotvvudivor

..)(, 
 
espaceespace
m dBAdivdArotBW 



)(
2
1
.
2
1
00

Cette expression reste valable pour des distributions quelconques de courants .
SdBAdBW
S
m

).(
2
1
2
1
0espace
2
0







espace
.
2
1
dAj


espace0
.
2
1


dABrot


38. 12- Tableau récapitulatif et comparatif
Electrostatique Magnétostatique
 







d
PM
PMPj
MB 3
0
4
)(




 
d
PM
PMP
ME  3
0
)(
4
1
)(

0
int
.

 S
S
Q
SdE  

 

i
iIdB 0. 

0

Ediv

VgradE 

ArotB


0

Erot
0

V jA

0
 



 PM
dP
MV i
04
1
)( 


d
r
Pj
MA
volume
)(
4
)( 0


)0.( 


dE 0Bdiv

jBrot

0
)0.( 
S
SdB

012

 tt EE
12
0
12 nEE nn




 1201t2t )BB( nK

 
012

 nn BB
0Adiv


39. Electrostatique Magnétostatique
)(
2
1
ii
i
iélec MVqW  

n
i
iim IW
12
1


volume
m dAjW 

.
2
1

volume
élect VdW 
2
1

espace
2
02
1
t
m dBW 

espaceltout
élec d
Eε
W
'
2
0
2

3
0
3
0
sin
4
et
cos
2
4 r
p
E
r
p
Er




  3
0
3
0 sin
4
et
cos
4
2
r
B
r
θ
B θr




 mm
