Ce document présente une étude sur la commande scalaire des machines asynchrones, mettant l'accent sur l'évaluation des performances et la maîtrise des risques technologiques. Il se concentre sur la modélisation des systèmes et les différents régulateurs utilisés pour contrôler la vitesse de la machine. Les résultats expérimentaux et de simulation sont comparés pour identifier les meilleures performances en termes de temps de réponse et rejet de perturbations.

1. Évaluation des Performances et Maîtrise
des Risques Technologiques pour les
Systèmes Industriels et Energétiques
EPMRT 28-29 mai 2009
GREAH, Université du Havre
Université des Sciences et de la Technologie Oran- M.B
Faculté Génie Electrique
Département d' Electrotechnique
Laboratoire LDEE
Contrôle de la Vitesse de la Machine Asynchrone
par Différents Régulateurs utilisant la Commande Scalaire.
Etude et Réalisation
Présenté par:
Pr M. Rahli
1

2. Commande scalaire de la machine asynchrone: étude et réalisation
Introduction générale
L’objectif de cette recherche consiste à étudier et appliquer les
différents régulateurs existant pour contrôler la machine
asynchrone par la commande scalaire en temps réel. Dans ce
travail nous nous attachons à comparer par simulation et
expérimentalement différents régulateurs afin d’obtenir les
meilleures performances à savoir, un temps de réponse rapide
suite à un changement de vitesse et une rapidité de rejet de
.perturbation
2

3. Commande scalaire de la machine asynchrone: étude et réalisation
P
L
I : Modélisation du système CS_MAS
II : Étude de la commande scalaire
A
N
III : Synthèse des régulateurs
Conclusion & Perspectives
3

4. Modélisation de convertisseur et de ses commandes MLI
Modélisation de la machine asynchrone
4

5. Chapitre 1 : Modélisation du système convertisseur statique _ MAS
Modélisation de convertisseur et de ses commandes MLI
m = 157, r = 0.9
m = 36, r = 0.9
1 .5
(v )
1
v a ,v b ,v c ,v p
v a ,v b ,v c ,v p
(v )
1 .5
0 .5
0
1
0 .5
0
-0 . 5
-0 . 5
-1
-1
-1 . 5
-1 . 5
0
0 .0 0 2
0 .0 0 4
0 .0 0 6
0 .0 0 8
0 .0 1
0 .0 1 2
Te m p s [s ]
0 .0 1 4
0 .0 1 6
0 .0 1 8
0 .0 2
S a
0 .5
-0 . 5
0 .0 0 6
0 .0 0 8
0 .0 1
0 .0 1 2
Te m p s [s ]
0 .0 1 4
0 .0 1 6
0 .0 1 8
0 .0 2
0 .5
0
0 .0 0 2
0 .0 0 4
0 .0 0 6
S e l e c0 .t 0e 0d 8 Tse im0 p0sa1 l[:s ]10 . 0 1y 2c l e0 s. 0 1 4
g .n
c
0 .0 1 6
0 .0 1 8
-0 . 5
0 .0 2
0
0 .0 0 2
0 .0 0 4
0 .0 0 2
0 .0 0 4
S e l e c0 t. 0 0d 8 Ts e i m0 np0s1 l [: s ]10 . c0 1 2c l e0 s. 0 1 4
e
g . a
y
0 .0 0 6
0 .0 1 6
0 .0 1 8
0 .0 2
4 205 00
1 0 0
1 0 0
5 0
(v )
2 0 0
2 105 00
0
v a n
2 0 0
2 105 00
0
-5 0
0
-1 0 0
-1 5 0
-2 5 0
0
-2 0 0
-1 0 0
- 4 200 00
-
5 0
-5 0
-2 0 0
-1 5 0
0
0 .0 0 5
0
0 .0 0 2
0 .0 0 4
0 .0 0 6
0 .0 1
0 .0 0 8
TTi e m0e .p0s(1s [ s) ] 0 . 0 1 2
m
0 .0 1 5
0 .0 1 4
- 4 200 00
-
0 .0 2
0 .0 1 6
0 .0 1 8
-2 5 0
0 .0 2
0
0 .0 0 5
0
F u n d a m e n ta l (5 0 H z ) = 1 4 0 .3 , T H D = 4 2 .0 1 %
0 .0 1
T Ti e m0e.p0s(1s [ s ] 0 . 0 1 2
m
)
0 .0 0 8
0 .0 1 5
0 .0 1 4
0 .0 2
0 .0 1 6
0 .0 1 8
0 .0 2
1 5 0
S p e c tre d e V a n
Fondamental=70.686%
Déchet de tension=29.314%
1 0 0
5 0
0
0 .0 0 6
F u n d a m e n ta l (5 0 H z ) = 1 4 0 .7 , T H D = 3 .4 8 %
1 5 0
S p e c tre d e V a n
0 .0 0 4
0
4 205 00
(v )
0 .0 0 2
1
0
v a n
0
1 .5
1
S a
1 .5
0
1 0
2 0
3 0
N u m é r o d 'h a r m o n i q u e
4 0
5 0
Fondamental=70.686%
Déchet de tension=29.314%
1 0 0
5 0
0
0
1 0
2 0
3 0
N u m é r o d 'h a r m o n i q u e
Simulation de la commande MLI sinus triangle pour m = 36 , r = 0.9
4 0
5 0
5

6. Chapitre 1 : Modélisation du système convertisseur statique _ MAS
Modélisation de la machine asynchrone
6

7. Chapitre 1 : Modélisation du système convertisseur statique _ MAS
Modélisation de la machine asynchrone
:Équations Générales de la Machine Asynchrone .1.1
Équations Électriques .1.1.1
a) statorique
d

v A = R si A +
ΦA

dt

d

ΦB
v B = R s i B +
dt

d

v C = R si C +
ΦC

dt

[ VABC ] = R s [ iΦ ] +
ABC
d
[
dt
ABC
]
b) rotorique
d

va = R ria +
Φa

dt

d

v b = R ri b +
Φb

dt

d

vc = R ric +
Φc

dt

d
[ Vabc ] = R r [ i abc ] + [ Φ abc ]
dt
7

8. Chapitre 1 : Modélisation du système convertisseur statique _ MAS
Modélisation de la machine asynchrone
: Transformation de PARK des grandeurs statorique et rotorique. 1.2
La transformation directe
La transformation inverse
[V ] = [ A ] [ V ]
dq s
[i ]
dq
s
s
[ V ] = [ A ] [V ]
−1
ABC
ABC
= [ A s ] [i ABC ]
s
−1
ABC
[A ] =
s
s
dq s
−1
ABC

 cosθ s

2
− sinθ s
3
 1/ 2



dq s
[ i ] = [ A ] [i ]
[ Φ ] = [ A ] [Φ ]
[Φ ] = [ A ] [ Φ ]
dq s
s
ABC
2π 

cos θ s −

3 

2π 

− sin  θ s −

3 

1/ 2
s
2π  

cos θ s +

3  


2π  

− sin  θ s +

3 


1/ 2



8
dq s

9. Chapitre 1 : Modélisation du système convertisseur statique _ MAS
Modélisation de la machine asynchrone
Les expressions de tensions statoriques et rotorique transformées
: deviennent
d
d

 v ds  
− L s ωs
Lm
− L m ωs 
   R s + Ls
dt
dt

  
d
d

 v qs  
L s ωs
R s + Ls
L m ωs
Lm

 = 
dt
dt

  
d
d
Lm
− L m (ωs − ωm ) R r + L r
− L r (ωs − ωm ) 
 0 
dt
dt

  
d
d 
   − L m (ωs − ωm )
Lm
L r (ωs − ωm )
R r + Lr


 0 
dt
dt 
 i ds 
 
 
i 
 qs 
 
 
 i dr 
 
 
 i qr 
 
(Choix du Référentiel (d-q .1.3
Trois types de référentiels peuvent être envisagés à savoir
 .Référentiel lié au stator
 .Référentiel lié au rotor
 .Référentiel lié aux champs tournants
9

10. Chapitre 1 : Modélisation du système convertisseur statique _ MAS
Modélisation de la machine asynchrone
: Cas de référentiel lié au champ tournant
Ce référentiel est caractérisé par la transformation des enroulements
statoriques et rotoriques dans un repère tournant à la vitesse de
: synchronisme . Il se traduit par les équations électriques suivantes

Vds


Vqs


V
 dr

Vqr


= Rs I ds
= Rs I qs
= Rr I dr
= Rr I qr
dφ ds
+
− ω sφ qs
dt
dφ qs
+
+ ω sφ ds
dt
dφ dr
+
− ω glφ qr
dt
dφ qr
+
+ ω glφ dr
dt
10

11. Chapitre 1 : Modélisation du système convertisseur statique _ MAS
Modélisation de la machine asynchrone
Expression du couple électromagnétique .1.4
Le couple électromagnétique est exprimé en fonction des
courants rotoriques et statoriques
Ce = (3/ 2) pM ( I dr I qs − I ds I qr )
Équation de la vitesse .1.5
J
dΩ
+ f Ω = (3/ 2) pM sr ( I qs I dr − I ds I qr ) − Cr
dt
11

12. Chapitre 1 : Modélisation du système convertisseur statique _ MAS
Modélisation de la machine asynchrone
Identification des paramètres de la machine asynchrone par la .1.6
méthode classique
Fig. .Présent la MAS à rotor bobiné
Test à vide -1
Test à rotor bloqué -2
Mesure de -3 Rs
l’essai de lâcher -4
Déterminer le frottement
Rs , Rr , Ls , Lr
Déterminer le moment d’inertie
12

13. Chapitre 1 : Modélisation du système convertisseur statique _ MAS
Modélisation de la machine asynchrone
250
30
27
14
200
12
20
150
10
C o u p le (N . m )
10
50
Ia (A )
V a ,V b ,V c (v )
100
0
3
0 .0
8
-5 0
-1 0
-1 0 0
8
5 .7
4
2
1 .2
0
-1 5 0
-2 0
-2
-2 0 0
-2 5 0
0
0 .0 0 5
0 .0 1
0 .0 1 5
0 .0 2
Te m p s [s ]
0 .0 2 5
0 .0 3
0 .0 3 5
-2 7
-3 0
0 .0 4
250
0
10
20
30
Te m p s [s ]
40
50
-4
60
0
30
27
20
30
Te m p s [s ]
40
50
60
0 .6
20
10
0 .4
200
0 .2
100
50
0
-5 0
10
0
Q rd ,Q rq (w b )
Ia lp h a ,Ib e ta (A )
V a lp h a , V b e t a (v )
150
3
0 .0
8
-1 0
-1 0 0
-0 .2
-0 .4
-0 .6
-1 5 0
-2 0
-0 .8
-2 0 0
-2 5 0
0
0 .0 0 5
0 .0 1
0 .0 1 5
0 .0 2
T e m p s [s ]
0 .0 2 5
0 .0 3
0 .0 3 5
-2 7
-3 0
0 .0 4
-1
0
10
20
30
Te m p s [s ]
40
50
60
-1 .2
0
10
20
30
Te m p s [s ]
40
50
60
200
30
1200
25
1000
950
190
180
20
800
V it e s s e (t r/ m )
160
15
I d , I q (A )
V d ,V q (v )
170
150
140
10
5
600
400
130
200
0
120
110
-5
0
100
-1 0
-2 0 0
0
10
20
30
Te m p s [s ]
40
50
60
0
10
20
30
Te m p s [s ]
40
50
60
0 2 .4 5
10
20
30
Te m p s [s ]
40
50
60
Simulation du modèle de la machine asynchrone
13

14. Commande scalaire de la machine asynchrone: étude et réalisation
Étude de la commande scalaire
Pour garantir la variation de la vitesse de la machine
asynchrone sur toute la plage de fréquence, les industriels
. ont également utilisé la loi (u/f) constante
Cette technique est facile d’implantation, moins coûteuse
. donnant aussi des performances statiques acceptables
Plusieurs commandes scalaires existent selon que l’on agit
sur le courant ou sur la tension. Elles dépendent surtout la
topologie de l’actionneur utilisé (Onduleur de tension ou de
courant).Et pour notre cas on a utilisé l’onduleur de tension
alimenté la machine asynchrone commandée par une
.commande scalaire (u/f)=cste
14

15. Commande scalaire de la machine asynchrone: étude et réalisation
Modèle de la machine asynchrone en régime permanent
dφ ds
− ω sφ qs
dt
dφ qs
Vqs = Rs I qs +
+ ω sφ ds
dt
dφ dr
− ω rφ qr
dt
dφ qr
Vqr = Rr I qr +
+ ω rφ dr
dt
Vds = Rs I ds +
Vdr = Rr I dr +
r
X = xd + jxq
r
Vs = vds + jvqs = Rs ( ids + jiqs ) + d ( φ ds + jφ qs ) / dt + jω s ( φ ds + jφ qs )
r
Vr = vdr + jvqr = Rr ( idr + jiqr ) + d ( φ dr + jφ qr ) / dt + jω r ( φ dr + jφ qr )
r
r
d φ s / dt = 0 d φ r / dt = 0
( )
( )
r
Vr = 0
ω r = gω s
r
r
r
Vs = Rs I s + jω sφ s
r
r
0 = Rr I r + jgω sφ r
r
r
V
φs = − j s
ωs
φs =
Vs
= cst
ω15
s

16. Commande scalaire de la machine asynchrone: étude et réalisation
Modèle de la machine asynchrone en régime permanent
Vs = φ sω s
ωs
Vs
ˆ
vas = Vs cos(ω s t )
2π
ˆ
vbs = Vs cos(ω s t −
)
3
2π
ˆ
vcs = Vs cos(ω s t +
)
3
MLI
Source continu
Onduleur
16
MAS

17. Commande scalaire de la machine asynchrone: étude et réalisation
Commande scalaire avec contrôle du rapport u/f
Quand la fréquence dépasse la fréquence nominale on est en
régime de défluxage (survitesse) la machine entre dans l’état
de saturation à cause de la tension saturé et ceci provoque
une diminution du rapport ainsi que le couple produit par la
.machine
17

18. Commande scalaire de la machine asynchrone: étude et réalisation
Commande scalaire avec contrôle du rapport u/f
Vs
= cst
ωs
Et quand la fréquence et faible l’équation
n’est pas
valable car la chute de tension statorique (tension ohmique) est
importante n’est plus négligeable .Pour éliminer ce problème il
faut compenser cette chute ohmique par une augmentation de
. l’amplitude des tensions statoriques pour les faibles valeurs
φs =

 Vsn Vs 0 
−
 Vs 0 + 
ω
ω sn ω s 0 



 V 
Vs =   sn  ω s
  ω sn 
V
 sn


18
s
if ω s p ω
s0
if ω s 0 ≤ ω s pω
if ω s ≥ ω
sn
sn

19. Commande scalaire de la machine asynchrone: étude et réalisation
III : Synthèse des régulateurs
La commande optimale (COP)
Régulateur retour d’état sans et avec le rejet de perturbation (RD)
RST à modèle de référence (RSTMR)
19

20. Commande scalaire de la machine asynchrone: étude et réalisation
III : Synthèse des régulateurs
laboratoire LDEE
.
x
x
Photo du banc d’essai
20

21. Commande scalaire de la machine asynchrone: étude et réalisation
III : Synthèse des régulateurs
: Identification du système
b0 z − 1 + b1 z − 2
G( z ) =
1 + a0 z − 1 + a1 z − 2
−1
a0 = − 0.049171577680
a1 = − 0.0027486668517
b0 = 0.12452572213
b1 = 0.08671952616
21

22. Commande scalaire de la machine asynchrone: étude et réalisation
La commande optimale (COP)
La commande optimale est obtenue, en minimisant le critère de performance
2
: suivant
1
 d Ω (t + 1) 
J=
∑
2
e(t + 1) 2 + Q 

2
 + R∆ u (t )

dt
2

1
 d Ω (t + 1) 
2
ϕ = : Avec + Q 
e(t + 1)
+ R∆ u (t )2 


2
dt




2

2
 Ω (t + 1) − Ω (t ) 
1 *
2
  Ω − Ω (t + 1)  + Q 
ϕ =
 + R [ u (t ) − u (t − 1) ] 



2
Te




dϕ
= 0 pour trouver la solution optimale (loi de commande
:(il faut que
du (t )
(
)
(
)
(
)
 a0b0  1 + Q '  + Q ' b0 Ω (t ) + a1b0  1 + Q '  Ω (t − 1) + R − b1b0  1 + Q '  u (t − 1) 







u (t ) = 
b0 2  1 + Q '  + R


(
)
22

23. 23

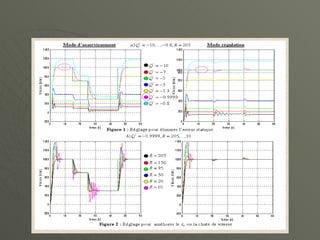
24. Commande scalaire de la machine asynchrone: étude et réalisation
La commande optimale (COP)
Les résultats pratique et simulation pour le régulateur COP
a. Cas de variation de vitesse et de couple
Variation de vitesse
Simulation
dépassement
(tr/min 1000 ,300 ,700 ,1000)
Pratique
27.7%
1 4 0 0
1 4 0 0
1 1 8 2 .7
1 0 4 3 .3
1 0 0 0
9 5 0
de perturbation
1 2 7 7
1 1 8 2 .7
1 0 0 0
9 5 0
V it e s s e (t r/ m )
1 2 7 7
V it e s s e (t r/ m )
Variation de couple
(Cr = 0, 1.2, 0 n.m)
rejet
8 0 0
7 0 0
6 0 0
4 0 0
8 0 0
6 0 0
tr=2 s
3 0 0
2 0 0
4 0 0
2 0 0
0
0
-2 0 0
-2 0 0
0
2
5 .3
1 0
1 5
2 0
2 5
3 0
T e m p s [s ]
4 0
4 5
5 0
6 0
8
0
2
5 .3
1 0
2 0
3 0
T e m p s [s ]
4 0
5 0
6 0
0
5 .3
1 0
2 0
3 0
T e m p s [s ]
4 0
5 0
6 0
0
5 .3
1 0
2 0
3 0
T e m p s [s ]
4 0
5 0
6 0
7
6 .3
6 .0 5
5
4 .5
4
C o u p le (N . m )
C o u p le (N . m )
6 .3
6 .0 5
5 .4
2
0
3
2
1 .2
0
-1 .3
-2 .1
-2 .4
-3 .1
-4
4
-2 .4
0
5 .3
1 0
1 5
2 0
2 5
3 0
T e m p s [s ]
4 0
4 5
5 0
-3
6 0
2 5
2 5
2 1 .5
2 1 .5
1 5
1 0
C o u ra n t (A )
C o u ra n t (A )
1 2 .8
1 0
6 .3
5
0 .8 8
0
-5
-6 .3
-1 0
-1 2 .8
5
3
0 .8 8
0
-5
-1 0
-1 5
-2 1 .5
-2 5
24
-2 1 .5
0
5 .3
1 0
1 5 1 7 .6
2 5 2 7 .6
T e m p s [s ]
4 0
4 5
4 9 .6
6 0
-2 5

25. Commande scalaire de la machine asynchrone: étude et réalisation
Régulateur retour d’état sans et avec le rejet de perturbation (RD)
: Retour d’état sans rejet de perturbation.1
K
: Calcul de
x( k + 1) = Fx( k ) + Gus ( k ) 

*
*
Ω s (k ) = Hx (k )
 ⇒ det( zI − ( F − GK ) ) = ( z − z1 )( z − z2 )

u (k ) = − Kx (k ) + Γ Ω * ( k ) 
 k1 = 0.1344
:
Calcul de
Γ

 k2 = 0.2102
Dans le régime permanant x(k + 1) = x( k ) et Ω (k ) = Ω (k ) ⇒
*
(
Γ = H ( I − A + GK ) G
Γ = 5.0078
25
−1
)
−1

26. Commande scalaire de la machine asynchrone: étude et réalisation
Régulateur retour d’état sans et avec le rejet de perturbation (RD)
Résultats de pratique et de simulation pour le régulateur Retour d’état sans.1.1
perturbation
rejet de perturbation
dépassement
Simulation
Variation de vitesse
0%(tr/min 1000 ,300 ,700 ,1000)
Variation de couple
(Cr = 0, 1.2, 0 n.m)
Pratique
1200
1200
1000
950
1000
950
800
800
700
600
V it e s s e (t r/ m )
V it e s s e (t r/ m )
600
400
300
400
200
200
0
0
-2 0 0
0 2
10
20
30
T e m p s [s ]
40
50
60
-2 0 0
0 2
10
20
30
T e m p s [s ]
40
50
60
26

27. Commande scalaire de la machine asynchrone: étude et réalisation
Régulateur retour d’état sans et avec le rejet de perturbation (RD)
: Retour d’état avec rejet de perturbation .2
K
: Calcul de
x (k + 1) = Fx (k ) + Gus (k )


Ω s (k ) = Hx (k )

*
*
*
 ⇒ det ( zI − ( F1 − G1 K1 ) ) = ( z − z1 )( z − z2 )( z − z3 )
u (k ) = − Kx (k ) − k I xI (k )

*
 k1 = 2.1344
xI (k + 1) = xI (k ) + (Ω ( k ) − Ω (k )) 


 k2 = 1.7873
 k = − 5.0078
 I
27

28. Commande scalaire de la machine asynchrone: étude et réalisation
Régulateur retour d’état sans et avec le rejet de perturbation (RD)
: Résultats de pratique et de simulation pour le régulateur RD avec le rejet .2.1
a. Cas de variation de vitesse et de couple
rejet
Variation de vitesse
(tr/min 1000 ,300 ,700 ,1000)
dépassement
32%
Simulation
Pratique 1 4 0 0
1 4 0 0
1 0 0 0
9 5 0
V it e s s e ( t r / m )
1 2 0 0
1 0 0 0
V it e s s e (t r/ m )
de perturbation
1 3 2 0
1 2 0 0
8 0 0
6 0 0
4 0 0
8 0 0
6 0 0
tr=1.94 s
2 0 0
-2 0 0
4 0 0
2 0 0
0
0
-2 0 0
0
1 0
2 0
3 0
T e m p s [s ]
4 0
5 0
6 0
1 2
01 .9 4
5 .8
1 0
2 0
3 0
T e m p s [s ]
4 0
5 0
6 0
1 0
2 0
3 0
T e m p s [s ]
4 0
5 0
6 0
1 0
2 0
3 0
T e m p s [s ]
4 0
5 0
6 0
1 2
1 0
1 0
8
8
6 .2 6
C o u p le (N . m )
C o u p le (N . m )
Variation de couple
(Cr = 0, 1.2, 0 n.m)
4
2
0
-1 .1 5
-2
- 2 .. 5
-2 8
6 .2 6
4
2
1 .2
0
-2
-2 .5
-5 .4
-7 .5
-8
-4
0
1 0
1 5
2 0
2 5
3 0
T e m p s [s ]
4 0
4 5
5 0
-5 .4
-6
6 0
3 0
2 0
0
4 0
3 0
2 7 .5
2 0
1 4
1 1
C o u ra n t (A )
C o u ra n t (A )
4 0
0 .0
8
1 1
3
0 .0
8
-1 1
-1 4
-1 1
-2 0
-2 0
-2 7 .5
-3 0
-3 0
-4 0
0
5
1 0
1 5 6 .8
1
2 5 6 .8
2
T e m p s [s ]
4 0
4 5
4 8
6 0
-4 0
28
0
5

29. Commande scalaire de la machine asynchrone: étude et réalisation
Régulateur retour d’état sans et avec le rejet de perturbation (RD)
Comparaison des résultats pour les régulateurs RD et COP
a. Cas de variation de vitesse et de couple
COP
Variation de vitesse
14 00
13 10
RD
140 0
131 0
1 1 8 2 .7
8 00
80 0
100 0
95 0
V it e s s e ( t r / m )
V it e s s e (t r/ m )
1 1 8 2 .7
11 20
10 40
10 00
9 50
Variation de couple
7 00
6 00
4 00
60 0
Simulation
40 0
3 00
2 00
20 0
0
0
-2 0 0
-2 0 0
0 2
5 .3
10
15
2 0
25
3 0
T e m p s [s ]
40
4 5
50
60
0
0
7
0
1 0
2 0
3 0
T e m p s [s ]
40
50
60
1 00 0
95 0
4
3
2
2
0
2
7
3
1 17 8
1 10 3
V it e s s e f ilt r é e ( t r / m )
1
1
1
1
V it e s s e f ilt r é e ( t r / m )
5 .3
1 40 0
1 32 0
10 00
9 50
0 2
8 00
7 00
6 00
4 00
80 0
Pratique
60 0
40 0
3 00
2 00
20 0
0
0
-2 0 0
-2 0 0
01 .9 4 5 .8
10
15
2 0
25
3 0
T e m p s [s ]
40
4 5
50
60
01 .9 4 5 .8
10
20
3 0
T e m p s [s ]
4 0
5 0
60
29

30. Commande scalaire de la machine asynchrone: étude et réalisation
Régulateur retour d’état sans et avec le rejet de perturbation (RD)
Chute de vitesse
0.6 %
Simulation
Chute de vitesse Augmentation de
RD 3.5% Pratique vitesse 17.8%
COP
1010
1300
1005
1250
1000
1178
V it e s s e f ilt ré e ( t r/ m )
V it e s s e ( t r/ m )
994
990
985
980
Chute de vitesse
3.1%
975
969
965
960
20
2 0 .5
21
2 1 .5
22
2 2 .5
T e m p s [s ]
23
2 3 .5
24
2 4 .5
1103
1000
965
940
900
Augmentation de
850
25
800
10
1 5
2 02 1 . 5
2 5
Chute de vitesse
30
3 5
4 0 4 2 .7
T e m p s [s ]
50
55
vitesse 10.5%
60
6%
30

31. Commande scalaire de la machine asynchrone: étude et réalisation
Régulateur retour d’état sans et avec le rejet de perturbation (RD)
b. Test de robustesse
Simulation
1400
1310
COP
RD
1 1 8 2 .7
1000
600
400
Très faible instabilité
1200
1000
950
V it e s s e f ilt ré e (t r/ m )
V it e s s e (t r/ m )
8 0 0 .0 9 5
Pratique
1400
1320
800
600
Test 1
400
200
200
100
100
0
0
-2 0 0
01 .9 4 5 .8
10
20
30
T e m p s [s ]
40
50
-2 0 0
60
01 .9 4 5 .8
10
20
25
30
T e m p s [s ]
40
50
60
Cas du Test 1 : Changement de vitesse de 1000 à 100 tr/min
1200
1085
1000
950
1090
1040
1000
950
800
800
V it e s s e f ilt ré e (t r/ m )
1400
1320
1 1 8 2 .7
V it e s s e (t r/ m )
1400
1310
600
400
300
Test 2
600
400
300
200
200
0
50
0
-2 0 0
-2 0 0
01 .9 4 5 .8
10
20
30
40
50
60
31
01 .9 4 5 .8
10
20
30 33
40
50
60

32. Commande scalaire de la machine asynchrone: étude et réalisation
RST à modèle de référence (RSTMR)
Modélisation RST de régulateur numérique.1
Bm ( z − 1 )
B( z − 1 )T ( z − 1 )
Ω ( z)
=
=
*
−1
−1
−1
−1
Ω ( z ) R( z ) A( z ) + S ( z ) B( z ) Am ( z − 1 )
:Alors
Am ( z − 1 ) = A( z − 1 ) R( z − 1 ) + B( z − 1 ) S ( z − 1 )
Si on souhaite que le processus ait une erreur statique nulle, il convient que
: le régulateur comporte une intégration
Am ( z − 1 ) = A( z − 1 ) H 2 ( z − 1 ) R ' ( z − 1 ) + B ( z − 1 ) S ( z − 1 )
4
3
2
2
123 14 244 123 1 3 1 3
4 4
AmBézout ( z − 1 )
: Alors
ABézout ( z − 1 )
RBézout ( z − 1 )
BBézout ( z − 1 ) S Bézout ( z − 1 )
deg( ABézout ( z − 1 )) = (deg( A( z − 1 ))) + i
32

33. Commande scalaire de la machine asynchrone: étude et réalisation
RST à modèle de référence (RSTMR)
Placement de pôles avec compensation de zéros .2
: régulation.2.1
: la première approche consiste à fractionné leB ( z − 1 ) sous la forme
B( z − 1 ) = B + ( z − 1 ) B − ( z − 1 )
: Alors le processus en boucle fermée devient
Bm ( z − 1 )
Ω ( z)
B − ( z − 1 )T ( z − 1 )
=
=
*
−1
−1
"
−1
−
−1
−1
Ω ( z ) A( z ) H 2 ( z ) R ( z ) + B ( z ) S ( z ) Am ( z − 1 )
: Par l’identification
Am ( z − 1 ) = A( z − 1 ) H 2 ( z − 1 ) R" ( z − 1 ) + B − ( z − 1 ) S ( z − 1 )
4
3
4 3 2
124 14 244 123 124 1 3
4 3
AmBézout ( z − 1 )
ABézout ( z − 1 )
RBézout ( z − 1 )
BBézout ( z − 1 ) S Bézout ( z − 1 )
: Poursuite d’échelon 2.2
Ω ( z ) B − ( z − 1 )T ( z − 1 )
=
*
Ω ( z)
Am ( z − 1 )
*
:Pour assurer la poursuite d’échelons, c’est-à-dire lim(Ω (k ) − Ω ( k )) = 0
k→ ∞
−1
: Alors
A (z )
T (z−1) = m −
B (1)
−
: Avec B (1) ≠ 0
33

34. Commande scalaire de la machine asynchrone: étude et réalisation
RST à modèle de référence (RSTMR)
(Poursuite suivi de consigne :(RST à modèle de référence.3
: D’après la figure 2 on déduire l’équation suivante
Bm ( z − 1 )
Ω ( z)
Ω ( z ) Ω * ( z ) Bm ( z − 1 ) Am ( z − 1 )
=
=
K
= K
Ω c ( z ) Ω * ( z ) Ω c ( z ) Am ( z − 1 ) Amc ( z − 1 )
Amc ( z − 1 )
Amc ( z − 1 )
:Avec K = lim
−1
z− 1 → 1 A ( z )
m
: Loi de commande s’exprime par
U ( z) =
1
( KAm ( z − 1 )T ( z − 1 ))Ω c ( z ) − ( Amc ( z − 1 ) S ( z − 1 ))Ω ( z )
Amc ( z − 1 ) R( z − 1 )
34

35. Commande scalaire de la machine asynchrone: étude et réalisation
RST à modèle de référence (RSTMR)
Les résultats pratique et simulation de régulateur RSTMR.4
a. Cas de variation de vitesse et de couple
dépassement
32 %
1 4 0 0
1 3 2 0
Variation de vitesse
(tr/min 1000 ,300 ,700 ,1000)
Simulation
Variation de couple
(Cr = 0, 1.2, 0 n.m)
Pratique 1 4 0 0
de perturbation
1 3 2 0
1 2 0 0
1 0 0 0
9 5 0
1 0 0 0
9 5 0
V it e s s e ( t r / m )
1 2 0 0
V it e s s e ( t r / m )
rejet
8 0 0
7 0 0
6 0 0
4 0 0
8 0 0
6 0 0
tr=1.95 s
3 0 0
2 0 0
0
-2 0 0
4 0 0
2 0 0
0
01 .9 5
7 .4 1 0
1 5
2 0
2 5
3 0
T e m p s [s ]
4 0
4 5
5 0
-2 0 0
6 0
1 5
01 .9 5
7 .4 1 0
2 0
3 0
T e m p s [s ]
4 0
5 0
6 0
0
1 0
2 0
3 0
T e m p s [s ]
4 0
5 0
6 0
0
7 .4 1 0
2 0
3 0
T e m p s [s ]
4 0
5 0
6 0
1 5
1 0
1 0
C o u p le (N . m )
C o u p le (N . m )
7 .2
6 .2 6
3 .5
2
0
-2
-2 .9
-4 .2
7 .2
6 .2 6
1 .2
0
-9
-3 .7
-5
-1 5
-2 0
0
1 0
1 5
2 0
2 5
3 0
T e m p s [s ]
4 0
4 5
5 0
-9
-1 0
6 0
4 0
4 0
3 0
3 0
2 0
1 6 .5
1 2 .5
1 0
1 8
C o u ra n t (A )
C o u ra n t (A )
2 5
0
-1 2 .5
-1 6 .5
-2 0
1 0
3
0 .0
8
-1 0
-1 8
-2 5
-3 0
-4 0
35
-3 0
0
7 .4 1 0
1 5
1 8 2 0
2 5
2 8 3 0
T e m p s [s ]
4 0
4 5
5 0 .2
6 0
-4 0

36. Commande scalaire de la machine asynchrone: étude et réalisation
RST à modèle de référence (RSTMR)
Comparaison des résultats pour les régulateurs RSTMR et RD
a. Cas de variation de vitesse et de couple
Variation de vitesse
1 400
1 310
RSTMR
1 000
950
1 00 0
95 0
800
Variation de couple
1 20 0
80 0
V it e s s e (t r/ m )
1 200
V it e s s e ( t r / m )
RD
1 40 0
1 32 0
700
600
400
Simulation
60 0
40 0
300
200
20 0
0
0
-2 0 0
01 .9 4 5 .8
10
15
20
2 5
30
T e m p s [s ]
40
4 5
5 0
-2 0 0
60
01 .9 5
1 0
20
3 0
T e m p s [s ]
40
5 0
60
1400
1320
1 4 0 0
1 3 2 0
1 2 3 0
1200
1107
1000
950
V it e s s e f ilt r é e ( t r / m )
V it e s s e f ilt r é e ( t r / m )
1 0 0 0
9 5 0
8 0 0
7 0 0
6 0 0
4 0 0
3 0 0
800
Pratique
600
400
1 8 0
200
0
0
-2 0 0
01 .9 5
7 .4 1 0
1 5
2 0
2 5
3 0
T e m p s [s ]
4 0
4 5
5 0
6 0
-2 0 0
01 .9 5
7 .4 1 0
20
30
T e m p s [s ]
40
50
60
36

37. Commande scalaire de la machine asynchrone: étude et réalisation
RST à modèle de référence (RSTMR)
Chute de vitesse
0.6 %
Chute de vitesse
RSTMR
Simulation
1010
RD %
3.8
1300
Pratique
Augmentation de
1007
1250
1000
9 9 7 .5
990
Chute de vitesse
2%
985
980
975
V it e s s e f ilt ré e (t r/ m )
1150
994
V ite s s e (t r/ m )
vitesse 10.7%
1200
1107
1050
1000
962
970
900
965
850
960
20
2 0 .5
21
2 1 .5
22
2 2 .5
T e m p s [s ]
23
2 3 .5
24
800
Augmentation de
Chute de vitesse
3.5%
2 4 .5
25
10
2 0 2 2 .8
30
vitesse 10.5%
40
43
50
60
T e m p s [s ]
37

38. Commande scalaire de la machine asynchrone: étude et réalisation
RST à modèle de référence (RSTMR)
b. Test de robustesse
Simulation
1400
1320
RSTMR
RD
1200
1000
Pratique
1400
1320
Très faible instabilité
1200
1000
950
V it e s s e f ilt ré e ( t r/ m )
V it e s s e (t r/ m )
800
600
330
200
100
0
800
600
Test 1
400
200
100
0
-2 0 0
-2 9 5
-4 0 0
0
10
20
30
T e m p s [s ]
40
50
-2 0 0
60
01 .9 5
7 .4 1 0
20
2628 30
T e m p s [s ]
40
50
60
Cas du Test 1 : Changement de vitesse de 1000 à 100 tr/min
1
1
1
1
4
3
2
2
0
2
7
0
1400
1320
0
0
0
0
1200
1095
800
V it e s s e f ilt ré e (t r/ m )
1000
950
800
V it e s s e (t r/ m )
1000
950
620
400
300
600
440
300
200
200
50
0
0
-9 0
-2 0 0
Test 2
38
-2 0 0
01 .9 5
10
20
30
40
50
60
01 .9 5
7 .4 1 0
20
30
40
50
60

39. Commande scalaire de la machine asynchrone: étude et réalisation
Conclusion générale
Dans ce article, nous avons traité la commande de la machine
asynchrone pour le fonctionnement en moteur sous
application des essais. Le développement de différents
algorithmes de commande a permis de mettre en évidence les
.performances et les limites de chaque méthode
Effectivement, nous avons pu voir à partir des résultats
obtenus, que la commande par retour d’état est plus
intéressante et permet d’obtenir un système performant, rapide
.et avec un très faible instabilité dans les basses vitesses
Cette méthode a permis d’avoir un fonctionnement meilleur en
éliminant l’effet de la perturbation, qui représente le principal
.souci dans les systèmes électromécaniques
39

40. Commande scalaire de la machine asynchrone: étude et réalisation
Perspectives
: Travaux futurs
Implantation en pratique et en simulation de nouveaux régulateurs backstepping, platitude, réseaux neurone,
.algorithme génétique, LMI
Estimer en pratique la vitesse de la machine par la méthode du filtre de kalman étendu, …, et comparer avec
d’autres méthodes
40

41. 41