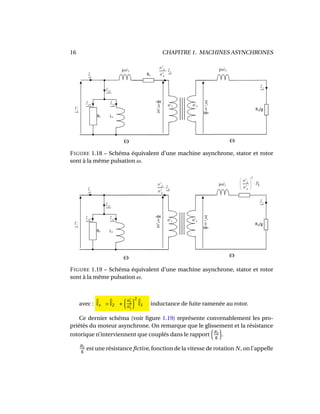
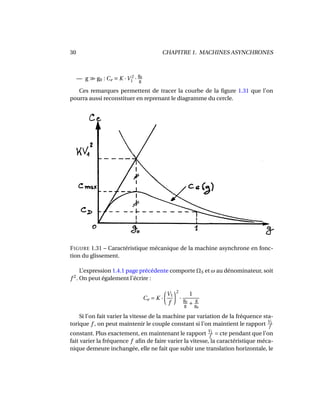
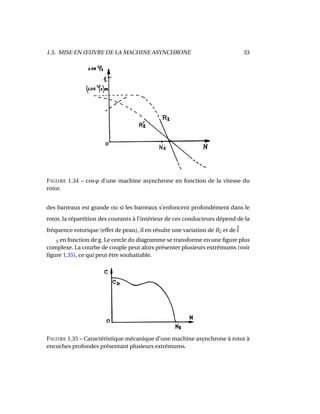
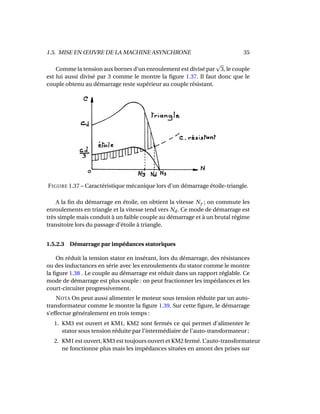
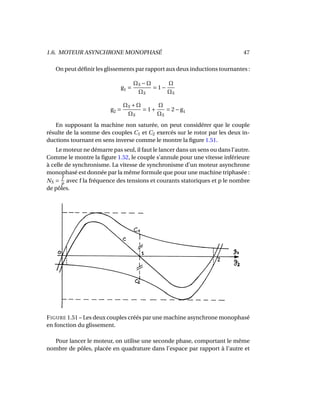
Le document traite des machines asynchrones, qui représentent environ 80% des moteurs utilisés dans le monde en raison de leur coût réduit et de leur robustesse. Il couvre leur structure, fonctionnement, glissement, et applications ainsi que des exercices et problèmes pratiques. Les machines asynchrones peuvent varier de quelques watts à des puissances considérables, comme celles utilisées dans les porte-avions et les grands paquebots.



























































![Bibliographie
[BAG05] Lotfi BAGHLI : Page web de lotfi baghli, 2005. site internet :
http ://www.baghli.com/.
[CH95] Jean-Pierre CARON et Jean-Paul HAUTIER : Modélisation et com-
mande de la machine asynchrone. Éditions Technip, 1995.
[LNS81] Jacques LESENNE, Francis NOTELET et Guy SEGUIER : Introduc-
tion à l’électrotechnique approfondie. Technique et Documentation,
1981.
65](https://image.slidesharecdn.com/cours-mat-170510122431/85/Cours-machine-asynchrone-cours-et-problemes-69-320.jpg)