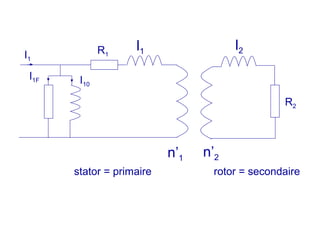
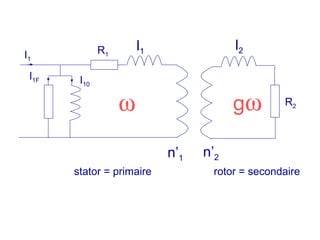
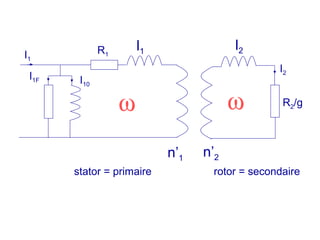
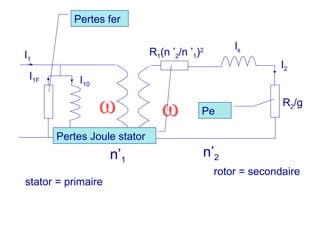
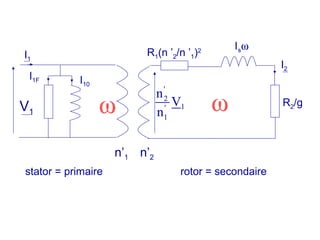
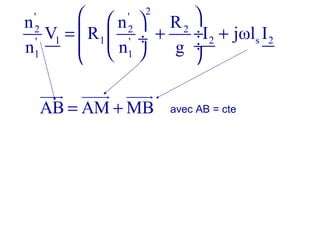
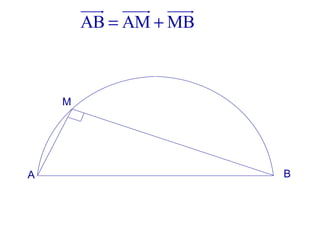
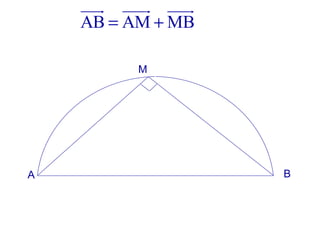
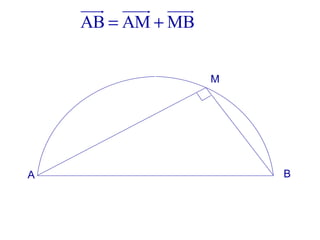
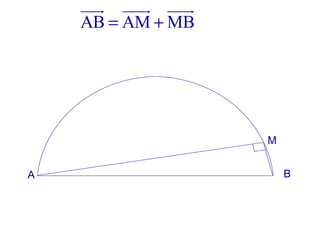
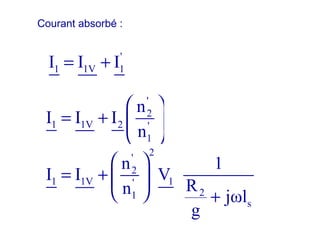
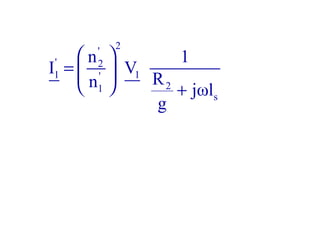
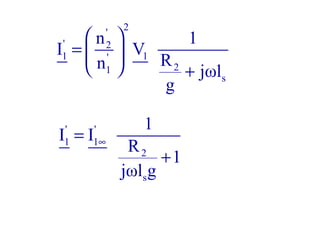
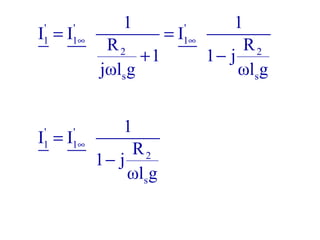
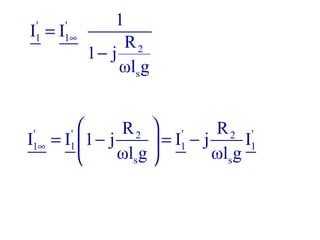
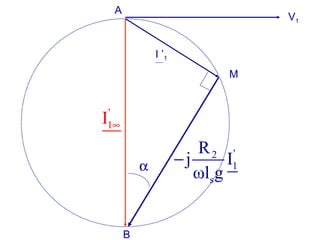
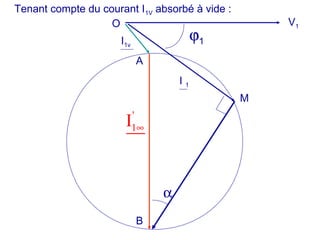
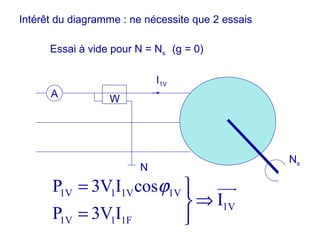
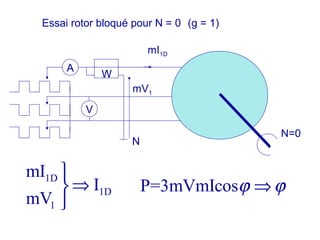
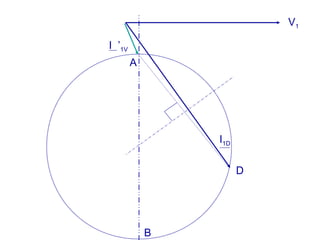
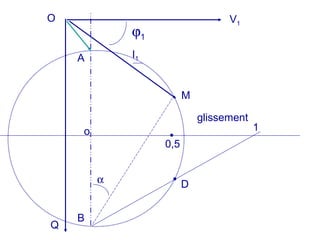
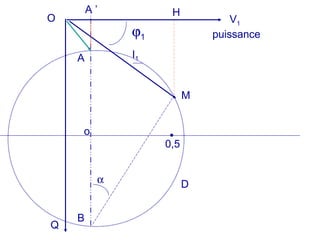
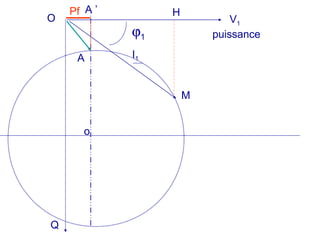
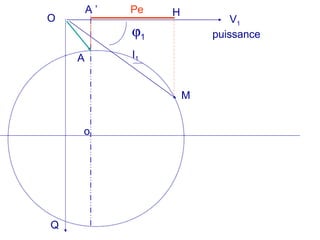
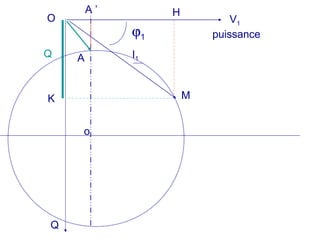
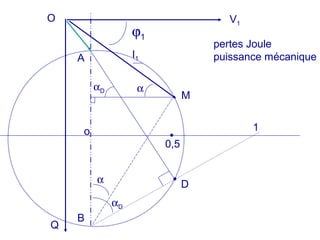
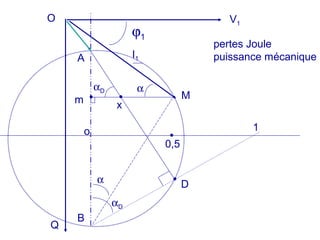
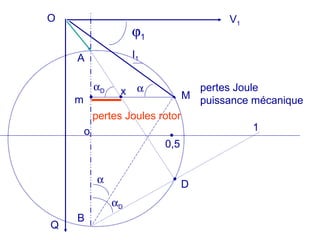
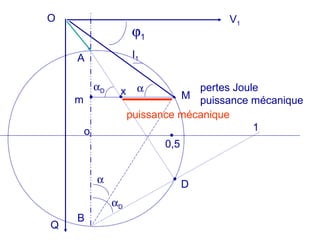
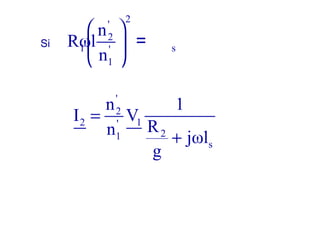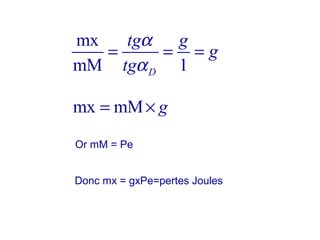La machine asynchrone est un transformateur à champ tournant où les courants statoriques et rotoriques engendrent des forces magnétomotrices. Le document aborde des concepts tels que les pertes joules, la puissance mécanique et les essais de fonctionnement. Il présente également des équations essentielles pour analyser le comportement de la machine dans différentes conditions de fonctionnement.

1. Machine asynchroneMachine asynchrone
diagramme du cerclediagramme du cercle

2. La machine asynchrone est un transformateur à
champ tournant.
Soit I1 le courant d ’une phase statorique,
soit I2 le courant d ’une phase rotorique.
Ces courants engendrent des
forces magnétomotrices tournantes de
vitesse Ns : n’1I1 et n’2I2, n’1et n’2 étant les
nombres de spires de chaque enroulement
corrigés par les coefficients de Kapp.

3. R1
I1F I10
n’1
I1
l1
stator = primaire
R2
n’2
l2
rotor = secondaire

4. 0 = j n ’2ω φ - j ω l2 I2 - R2 I2
g
V1 = j n ’1ω φ + j ω l1 I1 + R1 I1
Pour une phase du stator :
V2 = 0 = j n ’2(gω) φ - j (gω) l2 I2 - R2 I2
Pour une phase du rotor :

5. R1
I1F I10
n’1
I1
l1
stator = primaire
R2
n’2
l2
rotor = secondaire
ω gω

6. R1
I1F I10
n’1
I1
l1
stator = primaire
R2/g
n’2
l2
rotor = secondaire
ω ω
I2

7. R1(n ’2/n ’1)2
I1F I10
n’1
I1
stator = primaire
R2/g
n’2
ls
rotor = secondaire
ω ω
I2
Pertes fer
Pertes Joule stator
Pe

8. R1(n ’2/n ’1)2
I1F I10
n’1
I1
stator = primaire
R2/g
n’2
lsω
rotor = secondaire
ω ω
I2
V1
'
2
1'
1
n
V
n

9. Équation de maille rotorique :
'
2
2 1 2' '
1 2 2
1 s'
1
n 1
I V
n n R
R jωl
n g
=
 
+ + 
 
2
' '
2 2 2
1 1 2 2 s 2' '
1 1
n n R
V R I I jωl I
n n g
 
= + + 
 

10. 2
' '
2 2 2
1 1 2 s 2' '
1 1
n n R
V R I jωl I
n n g
  
= + + ÷ ÷ ÷  
AB AM MB= +
uuur uuur uuur
avec AB = cte

11. AB AM MB= +
uuur uuur uuur
A B
M

12. AB AM MB= +
uuur uuur uuur
A B
M

13. AB AM MB= +
uuur uuur uuur
A B
M

14. AB AM MB= +
uuur uuur uuur
A B
M

15. AB AM MB= +
uuur uuur uuur
A B
M

16. Hypothèse simplificatrice :
On néglige
2
'
2
1 '
1
n
R
n
 
 ÷
 

17. Si
2
'
2
1 s'
1
n
Rωl
n
 
 
 
=
'
2
2 1'
21
s
n 1
I V
Rn jωl
g
=
+

18. Courant absorbé :
'
2
1 1V 2 '
1
n
I I I
n
 
= +  
 
2
'
2
1 1V 1'
21
s
n 1
I I V
Rn jωl
g
 
= +  
  +
'
1 1V 1I I I= +

19. 2
'
' 2
1 1'
21
s
n 1
I V
Rn jωl
g
 
=  
  +

20. Lorsque la vitesse varie, seule la composante
'
1I varie
Soit
'
1I ∞ , la valeur de
'
1I Lorsque g=∞
2
'
' 2
1 1'
1 s
n 1
I V
n jωl
∞
 
=  
 

21. ' '
1 1
2
s
1
I I
R
1
jωl g
∞=
+
2
'
' 2
1 1'
21
s
n 1
I V
Rn jωl
g
 
=  
  +

22. ' ' '
1 1 1
2 2
s s
1 1
I I I
R R
1 1 j
jωl g ωl g
∞ ∞= =
+ −
' '
1 1
2
s
1
I I
R
1 j
ωl g
∞=
−

23. ' '
1 1
2
s
1
I I
R
1 j
ωl g
∞=
−
' ' ' '2 2
1 1 1 1
s s
R R
I I 1 j I j I
ωl g ωl g
∞
 
= − = − 
 

24. 2
'
' 2
1 1'
21
s
n 1
I V
Rn jωl
g
 
=  
  +
Pour dessiner les vecteurs, il est nécessaire de faire
apparaître le déphasage de I ’1 par rapport à V1

25. V1
I ’1
'2
1
s
R
j I
ωl g
−
'
1I ∞
A
B
M
α

26. s
2
ωl
tg =
R
gα
Si g=0, M est en A
Si g=∞, M est en B

27. Tenant compte du courant I1V absorbé à vide :
V1
I 1
'
1I ∞
α
I1v
ϕ1
O
M
A
B

28. Intérêt du diagramme : ne nécessite que 2 essais
Essai à vide pour N = Ns (g = 0)
Ns
A
N
W
I1V
1V 1 1V 1V
1V
1V 1 1F
P 3VI cos
I
P 3VI
ϕ= 
⇒
= 
uur

29. Essai rotor bloqué pour N = 0 (g = 1)
N=0
A
N
W
mI1D
V
mV1
1D
1D
1
mI
I
mV

⇒

P=3mVmIcosϕ ϕ⇒

30. V1
I ’1V
A
B
D
I1D

31. V1
A
B
M
I1
O
Q
ϕ1
α
o
D
1
0,5
glissement

32. V1
A
B
M
I1
O
Q
ϕ1
α
o
D
0,5
puissance
A ’ H

33. V1
A
M
I1
O
Q
ϕ1
o
A ’ HPf
puissance

34. V1
A
M
I1
O
Q
ϕ1
o
A ’ HPe
puissance

35. V1
A
M
I1
O
Q
ϕ1
o
A ’ H
Q
K
puissance

36. V1
A
B
M
I1
O
Q
ϕ1
α
o
D
1
0,5
pertes Joule
puissance mécanique
αD
ααD

37. V1
A
B
M
I1
O
Q
ϕ1
α
o
D
1
0,5
pertes Joule
puissance mécanique
αD
ααD
xm

38. mx
mM 1D
tg g
g
tg
α
α
= = =
mx mM g= ×
Or mM = Pe
Donc mx = gxPe=pertes Joules

39. V1
A
B
M
I1
O
Q
ϕ1
α
o
D
1
0,5
pertes Joule
puissance mécanique
αD
ααD x
m
pertes Joules rotor

40. V1
A
B
M
I1
O
Q
ϕ1
α
o
D
1
0,5
αD
ααD x
m
puissance mécanique
pertes Joule
puissance mécanique

41. V1
A
B
M
O
Q
o
D
1
0,5
x
m
moteur

42. V1
A
B
M
O
Q
o
D
1
0,5
x
m
frein

43. V1
A
B
M
O
Q
o
D
1
0,5
x
m
génératrice
- 0,5

44. That’s all Folks