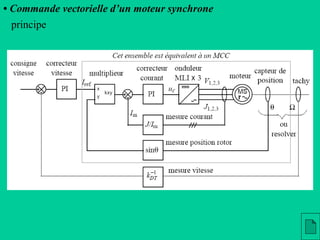
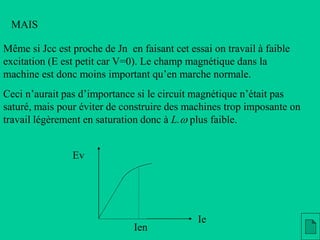
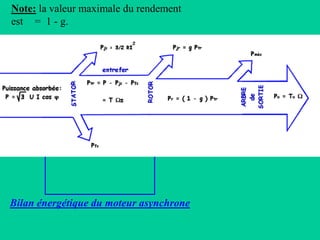
Le document examine le fonctionnement et les caractéristiques des machines synchrones, en mettant l'accent sur leur utilisation dans les applications de forte puissance et de faible puissance, comme les moteurs brushless. Il décrit les modèles électriques, le couple moteur, et les défis liés à la commande de ces machines, notamment la nécessité de maîtriser la vitesse et le couple. En outre, il aborde les méthodes de mesure et l'optimisation de l'excitation pour une operation efficace.

1. PAGE NOIRE

2. • Constitution
Machine synchrone
Pour les fortes puissances, le rotor est bobiné. Son alimentation est en courant continu
peut être assurée par un collecteur à deux bagues (beaucoup plus simple que celui d’une
MCC)
Pour les petites puissances (usuellement < 10 kW), le rotor est à aimants permanents.
N'ayant ni collecteur ni balais, le moteur est appelé "brushless".
Le stator identique à la machine asynchrone: bobinage polyphasé (en général branché
en Y), qui engendre un champ tournant.

3. • Utilisations :
Ils sont utilisés en forte puissance (1 à 10 MW - compresseur de pompe,
concasseur); toutefois pour faire varier la vitesse, il faut faire varier la
fréquence des courants statoriques.
Il faut un moteur auxiliaire pour les faire démarrer
Il a donc fallu attendre le développement de l’électronique de puissance pour
commander des moteurs autosynchrones ou synchrones auto-pilotés
(TGV Atlantique – 1981 : 8 moteurs de 1100kW ).
Dans le domaine des faibles puissances, les rotors sont à aimants permanents
(moteurs brushless).
L’intérêt de ces moteurs réside alors dans la régularité de la vitesse de
rotation (lecteur de disques et cassettes, programmateur, servomoteur).
Ils sont moins fragiles et ont de meilleures performances que les MCC (
vitesse:30000tr/min) mais sont plus difficiles à piloter.

4. • Modèle électrique :
Vitesse de synchronisme = vitesse du champ tournant :
Ws = w/p en rad/s ou ns = f/p en trs/s
loi des mailles (1) V = E + (RJ )+ jLw J
fcem (loi de Lenz) (2) E = dF/dt= jwF

5. Fonctionnement en moteur Fonctionnement en générateur
V.J.cosj>0
V.J.sinj>0
V.J.cosj>0
V.J.sinj<0
V.J.cosj<0
V.J.sinj>0
V.J.cosj<0
V.J.sinj<0
Jg est par convention dans le sens opposé à Jm
j 

j
w

j

j
w
w
V
E
RJm
jL Jm
RJm
jL Jm
V
w
V
E
RJg
jL Jg
Jg
Jg
E
RJg
jL Jg
V
Jm
Jm
E

6. La machine synchrone peut donc consommer ou fournir
de la puissance active et consommer ou fournir de la
puissance réactive ceci toujours en gardant sa fréquence
de rotation strictement égale à la fréquence du réseau
Il est même possible de régler l’excitation de la machine
de manière à avoir un cosj=0 on dit que l’excitation est
optimisée
Photo

7. 
j
V1
E
J1
w
jL J1
• Couple du moteur synchrone
Hr crée la fem E dans le bobinage de la phase 1 en
tournant à la pulsation w, on a
E=JwFr K (coefficient lié au bobinage)
donc E est en avance de p/2 par rapport à Hr. Le
déphasage entre J1 et E : est donc de p/2 -q
Hs est créé par la somme des courants J1, J2 et
J3 et est en phase avec J1
De plus en négligeant R qui est faible dans le
diagramme de Fresnel on remarque que
Ecos=V1cosj
Soit C= 3.E.J.cos  / w
On a C.w = P =3.V.J.cos j soit C= 3.V.J.cos j / w
C= 3.E.J.cos (p/2 –q) / w
C= 3.E.J. sin q / w

8. • Etude du couple du moteur synchrone
Le couple est maximum pour q=p/2
C= 3.E.J. sin q / w
Si la charge est telle qu’on obtient q=p/2 une légère augmentation
de celle ci et C va diminuer avec sinq; le moteur décroche et n’a
plus de couple.
Pour pouvoir maîtriser la rotation d’un tel moteur il faut connaître q
donc  angle entre J et E d’où le schéma de commande possible
suivant:
Comme pour une MCC le couple est proportionnel au courant et la
fcem à la vitesse de rotation.

9. • Commande vectorielle d’un moteur synchrone
principe

10. • Détermination des éléments du modèle
Pas de problème pour la mesure de R
Pour la mesure de Lw c’est plus délicat:
Faisons tourner la machine à l’aide d’un moteur auxiliaire.La MAS
est alors génératrice. Si l-on met en court-circuit les phases de
l’induit, la tension aux bornes de chacune d’elles est nulle; on peut
alors écrire
E=R.J.cc + j.L.w.Jcc
Le même essai à vide permet de déterminer E: Vv=E on peut alors
écrire
E²=(R.Jcc)² + (L.w.Jcc)²
Jcc
Jcc
R
E
L
)²
.
(
²
.

=
w
Soit :

11. Même si Jcc est proche de Jn en faisant cet essai on travail à faible
excitation (E est petit car V=0). Le champ magnétique dans la
machine est donc moins important qu’en marche normale.
MAIS
Ceci n’aurait pas d’importance si le circuit magnétique n’était pas
saturé, mais pour éviter de construire des machines trop imposante on
travail légèrement en saturation donc à L.w plus faible.
Ev
Ie
Ien

12. ALORS
Pour déterminer L.w on préfère un essai sur une charge purement
réactive. Dans ce cas pour obtenir le courant nominal dans une
phase (Jn), il faudra une excitation beaucoup plus importante donc
un champ magnétique plus important.
Dans le diagramme de Fresnel V et E seront quasi colinéaires (on
néglige R.J ) et on btient
L.w.J = Ev - V
J
V
Ev L.w.J
R.J

13. http://fr.wikipedia.org/wiki
http:// www.techno-science.net
http://sitelec.free.fr/cours/msyn.pdf
http://stielec.ac-aix-marseille.fr/
http://sciences-physiques.ac-dijon.fr/documents/PhysiqueAppliquee/PhysiqueAppliquee.htm
http://www.syscope.net
http://assocampus.ifrance.com
Guide du technicien
Physique appliquée term F3 NATHAN
Les bases de l’électrotechnique VUIBERT

14. Moteur asynchrone

15. Note: la valeur maximale du rendement
est = 1 - g.
Bilan énergétique du moteur asynchrone