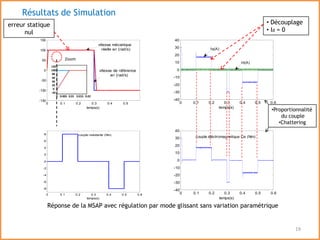
Ce mémoire présente la commande par mode glissant de la machine synchrone à aimants permanents (MSAP) et examine diverses méthodes de contrôle, y compris la commande vectorielle. Il détaille la modélisation, la simulation, et les résultats associés à l'application de la commande glissante, soulignant sa robustesse face aux perturbations. La conclusion met en avant la simplicité de mise en œuvre de cette technique, tout en notant les limites dues à l'effet de 'chattering'.

2. UNIVERSITE DJILLALI LIABES DE SIDI BEL ABBESFACULTE DES SCIENCES DE L’INGENIEURDEPARTEMENT D’ÉLECTROTECHNIQUEMémoirePour l’obtention du diplôme deMASTER EN ÉLECTROTECHNIQUEOption : Commande des Systèmes ElectriquesIntitulé:COMMANDE PAR MODE GLISSANT DE LA MACHINE SYNCHRONE A AIMANTS PERMANENTSPrésenté par :Mr : ATTOU Amine27 juin 2011

3. 1 Méthode de découplagecommande vectorielle à flux orienté Méthode de réglageContrôle par régulateur classique Contrôle par régulateur robusteMSAPVrefConvertisseurstatiqueDC-ACRégulateurclassiqueRégulateurRobusteOnduleuràMLIRéglageDécouplageFOCActionneurMesure électriqueMesure mécanique

4. Plan de travailGénéralités sur la machine synchrone à aimants permanents (MSAP)0102Modélisation de L’ensemble : Onduleur-MSAP 03 La commande vectorielle de la MSAP La commande par mode glissant de la MSAP04Conclusion

5. 3INTRODUCTION Le développement en parallèle de :l'électronique de puissance

6. les aimants permanents Majeur avantage : absence contacts glissantsaugmentation de la vitesse

7. la fiabilité

8. la robustesse de l’actionneur. Généralités sur la machine synchrone à aimants permanents (MSAP)

9. 4 Les Différents types de machines synchrones à aimants permanents aimantation radial1/ Rotor sans pièces polairesaimantation tangentielleLa structure de rotoraimantation radial2/ Rotor avec pièces polairesaimantation tangentielle

10. 51/Rotor sans pièces polairesa-Aimantation radialb-Aimantation tangentielle

11. 62/Rotor avec pièces polairesa-Aimantation tangentielleb-Aimantation radial

12. Modélisation de L’ensemble : Onduleur-MSAP

13. 7acAprès s’être basé sur les hypothèses simplificatrices, le modèle mathématique de la MSAP est présenté par la figure suivante:Modèle de parkModèle abciadvaparkθvbΦsfibbicvcqpark1234.

14. 8Equation électromagnétiqueEquation mécanique 12

15. 9E/2K1K2K3VaN0VbNVcNK3’K1’K2’-E/2SaSbScMLIMLIMLIPorteuseuaubucSchéma équivalent de l’onduleur à MLIModélisation de l’onduleur triphasé en tension Les systèmes d’équations peut s’écrire sous la forme matricielle :1

16. 10Schéma de SimulationLe modèle de la MSAP alimentée par onduleur de tension MLI est illustré par la figure ci dessous: Association onduleur (MLI-ST)-MSAP

17. Résultats de Simulationdiminution de vitesseCouple résistante Cr = 2 Nm couplage des courantsIqIdDéveloppement de couplecomportement de l’ensemble onduleur -MSAP avec application de la charge Cr = 2 Nm entre [0.3 0.5](s).1115

18. Commande vectorielle de la MSAP

19. 12Principe :maintenir le courant direct Idégal a zéro.

20. régulier la vitesse par le courant Iq.qVdIs=IqdVqId=0Isa0Principe de la commandevectorielleet12

21. Pour résoudre le problème de couplage entre les axes on utilise la méthode de compensation . Ce découplage est basé par l’introduction de termes compensatoires ed et eqAvec :Variables decommandeTermes decompensation123413.

22. 14Le principe de découplage par compensation est illustré par la figure suivante:compensationcompensationstructure générale : (machine-découplage par compensation).

23. 15Schéma de SimulationLe schéma bloc de simulation de la commande vectorielle de la MSAP est illustré par la figure suivante : Schéma globale de simulation de la commande vectorielle avec réglage classique (PI).

24. 16Résultats de SimulationContrôle du couple Découplage

25. Id = 0Rapidité de rejet Résultats de simulation de la commande vectorielle du MSAP avec réglage classique (PI), ω= - 100 rad/s à t= 0.6 s Cr = 8 Nm .

26. La commande robuste par mode glissant

27. 17La commande par mode glissant insensible aux : perturbations internes

28. perturbations externes

29. Variations paramétriques