Ce document constitue un mémoire de master sur la commande par mode glissant de la machine synchrone à aimants permanents, présenté par M. Attou Amine à l'Université Djillali Liabes. Il traite des caractéristiques, modélisations, et techniques de commande de ces machines, en attirant l'attention sur les avantages de l'électronique de puissance et des aimants permanents. Le travail est structuré en quatre chapitres, abordant successivement les généralités sur les machines synchrones, leur modélisation, la commande vectorielle, et enfin la commande par mode glissant.

1. REPUBLIQUE ALGERIENNE DEMOCRATIQUE ET POPULAIRE
MINISTERE DE L'ENSEIGNEMENT SUPERIEUR ET DE LA RECHERCHE SCIENTIFIQUE
UNIVERSITE DJILLALI LIABES DE SIDI BEL-ABBES
Faculté des Sciences de l'Ingénieur
Département d'Électrotechnique
Projet de Fin d’Etude présenté par :
M. ATTOU Amine
Pour l'obtention du diplôme de :
Master en Électrotechnique
Parcours : Commande des Systèmes Electriques
Intitulé du mémoire :
Commande par mode glissant de la machine
synchrone à aimants permanents
Présenté devant le jury composé de :
Dr : M. ABID MCA UDL Sidi bel - Abbés Président
Dr : A. MASSOUM MCA UDL Sidi bel - Abbés Encadreur
Dr : A. BENTAALLAH MCB UDL Sidi bel - Abbés Examinateur
Dr : A. AYAD MCB UDL Sidi bel - Abbés Examinateur
Soutenue le : 27 Juin 2011

2. Remerciements
J
e souhaite tout particulièrement exprimer ma gratitude à mon encadreur,
Dr A.MASSOUM, Maître de conférences (A) à l’université Djillali Liabes,
pour la confiance qu'il m'a témoignée en m'accueillant, pour m’avoir offert
un sujet aussi riche et passionnant, pour son suivi permanent et ses
conseils judicieux. Merci surtout de m’avoir accompagné malgré votre
emploi du temps assez chargés.
J
e remercie Monsieur ABID, Maître de conférences (A) à l’université Djillali
Liabes, pour l'intérêt qu'il a manifesté à mon travail en acceptant de le
juger et de présider le jury de soutenance. Je remercie également
Monsieur BENTAALLAH et Monsieur AYAD, Maîtres de conférences (B) à
l’université Djillali Liabes d’avoir accepté la mission de m’examiner et de
participer à ma soutenance.
J
e remercie tous les enseignants qui ont participé à notre formation et
toutes les personnes qui, de près ou de loin mon apportés leur soutien.

3. SOMMAIRE

4. SOMMAIRE
Abréviations et notations ……………………………………………………………………………………………………………………………….……. i
Introduction générale …………………………………………………………………………………………………………………………………………… 1
Chapitre 01
Généralités sur la machine synchrone à aimants permanents
I.1 Introduction …………………………………………………………………………………………………………………………………………………………….3
I.2 Présentation de la machine synchrone à aimants permanents …………………………………………………………… 3
I.2.1 Structure des inducteurs des machines à aimants………………………………………………………………………………...5
I.2.1.a Structure sans pièce polaire …………………………………………………………………………………………………………..5
Aimantation radial
Aimantation tangentielle
I .2.1.b Structure avec pièce polaire……………………………………………………………………………….…………….…………… 5
Aimantation tangentielle
Aimantation radial
I.2.2 Propriétés diamant permanent ………………………………………………………………………………………………………….……6
I.2.3 Choix d’aimants permanents utilisés pour la MSAP ……………………………………………………………………….….7
I.3 Avantage des machines synchrones à aimants ………………………………………………………………………….……………… 8
I.4 Domaine d’application…………………………………………………………………………………………………………………………………….…… 9
I.5 Conclusion ………………………………………………………………………………………………………………………………………………………….…… 9
Chapitre 02
Modélisation de l’ensemble Convertisseurs-MSAP
II.1 Introduction.………………………………………………………………………………………………………………………………………………………...
10
II.2 Hypothèses simplificatrices. …………………………………………………………………………………………………………………………. 10
II .3 Modélisation de la MSAP ………………………………………………………………………………………………………………………………… 10
II.3.1 Mise en équation de la MSAP en triphasé (modèle en abc) ……………………………………………………… 10
II.3.1.a Équation électrique ……………………………………………………………………………………………………………………… 10
II.3.1.b Équation électromagnétique ……………………………………………………………….…………………………………… 12
II.3.1.c Équation mécanique…………………………………………………………………………………………………………….………… 12
II.3.1.d La puissance absorbée………………………………….………………………………………………………………….…………… 12
II.3.2 Mise en équation de la MSAP en diphasé (modèle vectoriel) …………………………………….……………. 13
II.3.2.1 principe de la transformation de Park (composantes d-q) …………………………………………….. 13
II.3.2.2 principe de la transformation de CONCORDIA……………………………………………………………………… 14
UDL – Sidi bel Abbés - 2011 i

5. II.3.2.3 Passage du repère (d q) au repère (   ) …………………………………………………………….………..……. 15
II.3.3 Modélisation de la MSAP dans le repère de PARK ………………………………………………………………………… 15
II.3.3.a Équation électrique ………………………………………………………………………………………………………………………. 15
II.3.3.b Équation électromagnétique ……………………………………………………………………………………….……………. 16
II.3.3.c Équation mécanique ……………………………………………………………………………………………………..……..………… 16
II.3.4 Mise sous forme d’équation d’état ………………………………………………………………………………………….………… 16
II.4 Modélisation de convertisseur …………………………………………………………………………………….……………………….………… 17
II.4.1 Modélisation du redresseur ………………………………………………………………………………………………………..…..……… 18
II.4.2 Modélisation du filtre………………………………………………………………………………….………………………………..…..……… 18
II.4.3 Modélisation de l'onduleur………………………………………………………………………………………………………………..……… 19
II.4.3.1 Définition de l’onduleur de tension …………………………………………………………………………………….…… 19
II.4.3.2 Modélisation de l’onduleur de tension……………………………………………………………………………..……… 19
II.4.3.3 Commande de l’onduleur ………………………………………………………………………………………………..……….…… 20
a) Principe de la commande MLI………………………………………………………………………………………...….……… 20
b) Caractéristique de la MLI ………………………………………………………………………………………………...………… 20
II.5 Simulation numérique ………………………………………………………………………………………………………………………....…….………22
II.5.1 résultats de simulations ……………………………………………………………………………………………………….……………….. 23
II.5 .2 Interprétation des résultats ……………………………………………………………………………………………………..…………… 24
II.6 Conclusion……………………………………………………………………………………………………………….………………………..………..……………24
Chapitre 03
Commande vectorielle de la MSAP
III.1 Introduction. …………………………………………………………………………………………………………………………………………….….……… 25
III.2 Principe de la commande vectorielle .………………………………………………………………………………………….…….………25
III.3 Commande vectorielle direct par compensation ……………………………………………………………………….…….…… 26
III.3.1 Techniques de découplage………………………………………………………………………………………………………….….……… 26
III.3.2 Découplage par compensation.………………………………………………………………………………………………….…….……27
III.4 Détermination des régulateurs ………………………………………………………………………………………………………….…….…… 29
III.4.1 Description du système global.…………………………………………………………………………………………….……….………29
III.4.2 Calcul des régulateurs. ……………………………………………………………………………………………………………….….……… 30
III.4.3 Dimensionnement des régulateurs …………………………………………………………………………………………..….……… 31
a- Régulateur du courant « Iq » ………………………………………………………………………………………………….….……… 32
b- Régulateur du courant « Id » ……………………………………………………………………………………………….….………… 33
c- Régulation de vitesse ………………………………………………………………………………………………………….….…………… 34
III.5 Limitation des courants……………………………………………………………………………………………………………………….……….……35
III.6 Schéma global de simulation……………………………………………………………………………………………………………….………… 36
III.6.1 Résultats de simulation …………………………………………………………………………………………………………….…………… 37
III.7 Interprétation des résultats ……………………………………………………………………………………………………………….…………. 37
III.8 CONCLUSION……………………………………………………………………………………………………………………………………………….………… 38
UDL – Sidi bel Abbés - 2011 ii

6. Chapitre 04
Commande par mode glissant de la MSAP
IV.1 Introduction……………………………………………………………………………………………………………………………………………………………. 39
IV.2 Généralités sur la théorie du contrôle par mode glissement ………………………………………………………………. 39
IV.3 L’objectif de la commande par mode glissant……………………………………………………………………….………………….40
IV.4 Principe de la commande à structure variable ……………………………………………………………………….………………. 40
IV.4 .1 Définition des systèmes non linéaires ……………………………………………………………………………………………….
40
IV.4 .2 Formulation des expressions générales de la commande par mode de glissement …………
42
IV.4 .3 Condition pour l’existence du mode de glissant ……………………………………………………………………………. 42
IV.5 Les modes de la trajectoire dans le plan de phase ………………………………………………………………………………. 43
IV.6 Conception de la commande par mode glissant………………………………………………………………………………………. 43
IV.6.a Choix de la surface de glissement……………………………………………………………………………………………………….. 44
IV.6.b Conditions de convergence…………………………………………………………………………………………………………………….. 45
IV.6.b.1 Fonction directe de commutation………………………………………………………………………………………… 45
IV.6.b.2 Fonction de Lyapunov……………………………………………………………………………………………………………….. 46
IV.6.c Calcul la loi de commande…………………………………………………………………………………………………………………. 46
IV.7 Définition des grandeurs de commande……………………………………………………………………………………………………… 47
IV.8 Expression analytique de la commande………………………………………………………………………………………………………..48
IV.9 Phénomène de chattering ………………………………………………………………………………………………………………………….……. 49
IV.10 Elimination du phénomène de chattering ……………………………………………………………………………………………. 50
IV.10.1 Commande discontinue de base ……………………………………………………………………………………………………….. 50
IV.10.2 Commande avec un seuil………………………………………………………………………………………………………………………. 51
IV.10.3 Commande adoucie ……………………………………………………………………………………………………………………………….. 52
IV.10.4 Commande continue avec composante intégrale ………………………………………………………………………..53
IV.10.5 Utilisation d’une surface augmentée ……………………………………………………………………………………………… 54
IV.11 Application de la commande par mode de glissement à la MSAP ………………………………………………….. 54
IV.11.a Stratégie de réglage à trois surfaces ……………………………………………………………………………………….……… 54
IV.11.a.1 Réglage de la vitesse .……………………………………………………………………………………………..………….……….55
IV.11.a.2 Réglage du courant direct ………………………………………………………………………………………………..……….56
IV.11.a.3 Réglage du courant quadratique ……………………………………………………………………………………………… 57
IV.11.b Résultat de simulation ………………………………………………………………………………………………………………………… 58
IV.11.b.1 Test de robustesse ……………………………………………………………………………………………………………….…….. 59
a- Test de robustesse par rapport à la variation de la résistance statorique ….………… 60
b- Test de robustesse par rapport à la variation de moment d’inertie J……………………….60
c- Interprétation ……………………………………………………………………………………………………………………………...61
IV.11.b.2 Conclusion ……………………………………………………………………………………………………………………………………...61
Conclusion générale …………………………………………………………………………………………………………………………………………….…….. 62
ANNEXE …………………………………………………………………………………………………………………………………………………………………………..… 63
Bibliographie …………………………………………………………………………………………………………………………………………………………………… 64
UDL – Sidi bel Abbés - 2011 iii

7. NOTATIONS ET ABREVIATIONS

8. NOTATIONS ET ABREVIATIONS
MSAP : machine synchrone à aimants permanents.
MCC : machine à courant continu.
(abc) : modèle réelle de la machine triphasé.
(d-q) : modèle de Park.
MLI : modulation de largeur d’impulsion.
CSV : Commande à structure variable.
φ ,φ f sf : flux engendré par les aimants.
Rs : la résistance statorique.
Xa,b,c : composante réel dans le repère abc.
Ia,b,c : courants suivant les phases triphasées.
Xd : composante longitudinale suivant l’axe d.
Xq : composante transversale suivant l’axe q.
Id : courant de l’axe d.
Iq : courant de l’axe q.
ed et eq : termes de découplages.
θ : Angle électrique.
 : La pulsation électrique.
p : nombre de paires de pôles.
 r : Vitesse de rotation mécanique.
Cem : Couple électromagnétique.
Cr : Couple résistant.
J : Moment d’inertie.
f : Coefficient de frottement.

X , X ref : Valeur de référence.
UDL – Sidi bel Abbés - 2011 I

9. INTRODUCTION GENERALE

10. Introduction générale
INTRODUCTION GENERALE
Durant ces dernières années, les composants de l’électronique de puissance ont subi une grande
évolution avec l’apparition de composants interrupteurs rapides, ainsi que le développement des
techniques de commande. Cette apparition à permis de concevoir des convertisseurs statiques capables
d’alimenter en amplitude et en fréquence variable les moteurs à courant alternatifs. Le collecteur
mécanique de la machine à courant continu à été remplacé par des inducteurs de type aimants
permanents dans le cas ou les machines sont à courant alternatives qui permis de supprimer les
contacts glissants. Le développement en parallèle de l'électronique de puissance et des aimants
permanents ont conduit à la conception d'un nouveau type de machine synchrone excitée par des
aimants permanents d’où le nom : Machine Synchrone à Aimants Permanents (MSAP).
Aujourd’hui, les moteurs synchrones à aimants permanents sont recommandés dans le monde
industriel. Ceci est dû au fait qu’ils sont fiables, le moteur synchrone à aimants permanents à une
vitesse de rotation proportionnelle à la fréquence d’alimentation et, il est moins encombrants que les
moteurs à courant continu grâce à l’élimination de la source d’excitation. Ainsi, leur construction est
plus simple puisque il n’appartient pas un collecteur mécanique qui entraîne des inconvénients majeurs
tels que la limitation de puissance, l’usure des balais et les pertes rotoriques. Par conséquent, ceci
augmente leur durée de vie et évite un entretien permanent.
La machine synchrone à aimants permanents est connue par sa robustesse qui permet de créer des
commandes de vitesse et de couple avec précision et des performances dynamiques très intéressantes
(actionneurs de robotiques, servomoteurs, entrainement à vitesse variable…etc.). Mais sa commande
est plus compliqué que celle d’une machine à courant continue ; car le système est non linéaire et il
est très difficile d’obtenir le découplage entre le courant induit et le courant inducteur. Afin de
faciliter notre étude on doit modéliser notre machine suivant les axes d-q donc, on abordera le passage
du repère triphasé au repère biphasé par le biais de transformation de Park et on établira les équations
électriques et mécaniques de la machine synchrone à aimants permanents.
La commande vectorielle « field oriented control » permet à la machine synchrone à aimants
permanents d'avoir une dynamique proche de celle de la machine à courant continu qui concerne la
linéarité et le découplage.
Cependant, cette structure de commande nécessite que les paramètres de la machine soient précis,
ceci exige une bonne identification des paramètres. En conséquence, le recours à des algorithmes de
commande robuste, pour maintenir un niveau de découplage et de performance acceptable est
nécessaire.
UDL – Sidi bel Abbés - 2011 1

11. Introduction générale
La commande à structure variable qui par sa nature non linéaire, possède cette robustesse. Le
réglage par mode de glissement est fondamentalement une méthode qui force la réponse à glisser le
long d'une trajectoire prédéfinie. Cependant, cette technique de commande à un inconvénient de
commutation aux hautes fréquences (effet de chattering).
Dans notre travail, nous nous intéressons à l’étude des machines synchrones à aimants permanents
triphasé à pôles saillant alimentées par un onduleur commandé par la technique modulation de largeur
d’impulsions.
Ce mémoire s'articule en quatre chapitres :
Dans le premier chapitre, nous commençons par les caractéristiques générales des principaux
matériaux pour aimants permanents, puis nous présentons les différentes structures envisageables des
inducteurs des MSAP. A la fin du chapitre, nous citons les principaux avantages des Machines synchrones
à aimants permanents et leurs domaines d’application.
Le second chapitre concerne la modélisation de la machine synchrone à aimants permanents dans le
repère (abc), ainsi que dans le repère de Park (d-q) et on termine le chapitre par une étude de
l’association Machine-onduleur.
Le troisième chapitre décrit le principe de la commande vectorielle de la MSAP pour l'asservissement
de vitesse. La vitesse est réglée par un régulateur proportionnel intégral (PI).
L'intégration d'un régulateur par mode glissant, constitue l'objet du quatrième chapitre. Pour cela,
nous allons introduire dans un premier temps les notions générales sur la commande à structure
variable, on présentant les principes théoriques de cette commande où le système est contraint à
suivre la référence d’attractivité sans tenir compte du modèle de la machine
Nous terminerons par une conclusion générale en proposant des perspectives.
UDL – Sidi bel Abbés - 2011 2

12. CHAPITRE I
Généralités sur la machine synchrone
à aimants permanents

13. CHAPITRE : I Généralités sur la machine synchrone à aimants permanents
I.1 INTRODUCTION
Pendant plusieurs années, l’industrie a utilisé le moteur à courant continu (CC) offrant le Principal
avantage d’être facilement commandable grâce au découplage naturel du flux et du couple. Cependant
la présence du système balais collecteur a toujours été un grand inconvénient du moteur parmi d’autres
qui limitant de plus en plus son utilisation [3][14].
Cependant, la fragilité du système balai collecteur a toujours été un inconvénient de la M.C.C, ce
qui limite la puissance et la vitesse maximale et présente des difficultés de maintenance et des
interruptions de fonctionnement. C’est pour cette raison qu’on a eu intérêt à utiliser des moteurs
électriques à courant alternatif afin d’écarter cet inconvénient.
Parmi les moteurs à courant alternatif utilisés dans les entrainements à vitesse variable, le
moteur synchrone à aimants permanents reste un bon candidat. Son choix devient attractif et
concurrent de celui des moteurs asynchrones grâce à l’évolution des aimants permanents qu’ils soient à
base d’alliage ou à terre rare. Cela leur à permis d’être utilisés comme inducteur dans les moteurs
synchrones offrant ainsi, par rapport aux autres type de moteur, beaucoup davantage, entre autres,
une faible inertie et un couple massique élevé [15][25].
I.2 PRESENTATION DE LA MACHINE SYNCHRONE A AIMANTS PERMANENTS [6][15]
La machine synchrone à aimants permanents est un dispositif électromécanique qui comprend un
stator et un rotor.
Fig. I.1 : MSAP utilisée pour les validations expérimentales.
UDL – Sidi bel Abbés - 2011 3

14. CHAPITRE : I Généralités sur la machine synchrone à aimants permanents
Fig. I.2.a: stator d’une machine synchrone Fig. I.2.b: Photographie d’un rotor MSAP
 Le stator est une partie fixe induit où se trouvent les enroulements liés à la source, il est
semblable au stator de toutes les machines électriques triphasées, il est constitué d’un empilage de
tôle magnétique qui contient des encoches dans lesquelles sont logés trois enroulements identiques
2
décalés entre eux de .
3
Concernant son fonctionnent, il est basé sur le principe de rotation du champ magnétique en
synchronisme avec le rotor (vitesse de rotation identique entre le rotor et le champ tournant
statorique) ; d’où le nom des machines synchrone à aimants permanents (MSAP).
La vitesse de rotation du champ tournant est proportionnelle au nombre de pôles de la machine et à
la pulsation des courants statoriques. On note [17] :

r (1.1)
p
Avec :
 r : La vitesse de rotation de la machine (rad/s)
 : La pulsation des courants statoriques (rad/s).
p: Le nombre de paire de pôles de la machine.
 Le rotor est une partie mobile « inducteur » qui est monté sur l’axe de rotation, c’est un
noyau de fer sur lequel sont disposées des aimants permanents qui servent à générer une
excitation permanente.
Le rotor de la MSAP est généralement de deux types [15] :
 Rotor sans pièces polaires, donc à entrefer constante, dans lequel les aimants sont orientés
soit perpendiculairement à l’entrefer (aimantation radial) figure (I.3), soit parallèlement
(aimantation tangentielle) figure (I.4).
 Rotor possédant des pièces polaires, l’aimantation soit tangentielle figure (I.5) soit radiale
figure (I.6) .Dans ce type de machine, l’inducteur est à pôles saillants.
UDL – Sidi bel Abbés - 2011 4

15. CHAPITRE : I Généralités sur la machine synchrone à aimants permanents
I.2.1 STRUCTURE DES INDUCTEURS DES MACHINES A AIMANTS [29]
I.2.1.a Structure sans pièce polaire (SPP)
 Aimantation radiale
Allure d’une
ligne de champ Stator (encoches et
Air enroulements triphasés)
Stator
Cale (Circuit magnétique)
amagnétique
Rotor
(Circuit amagnétique)
Aimant permanent
Fig. I.3 : Machine synchrone à aimants (P=2), sans pièce polaire,
Aimantation radiale.
Les aimants de types alnico ou ferrite sont bien adaptés à cette structure, l’entrefer « e » peut être
considéré comme constante (machine à pôles lisses), le flux dans celui-ci est faible, cette structure est
essentiellement utilisée dans les machines synchrones de petite puissance.
 Aimantation tangentielle Allure d’une
ligne de champ
Air Cale amagnétique
Stator
(Circuit magnétique)
Aimant permanent Rotor
(Circuit amagnétique)
Fig. I.4 : Machine synchrone à aimants (P=2), sans pièce polaire,
Aimantation tangentielle.
En utilisation des aimants à aimantation tangentielle, on peut réaliser des machines à induction
sinusoïdale. La machine est à pôles lisses, l’induction est faible dans l’entrefer et le couple massique
reste faible.
I.2.1.b Structure avec pièce polaire (APP)
 Aimantation tangentielle
UDL – Sidi bel Abbés - 2011 5

16. CHAPITRE : I Généralités sur la machine synchrone à aimants permanents
Allure d’une ligne
De champ
Air
Stator
(Circuit magnétique)
Zone de concentration
de flux
(pièce polaires magnétiques)
Fig. I.5 : Machine synchrone à aimants (P=4), avec pièce polaire,
Aimantation tangentielle
L’aimant est à base de terre-rare, et les pièces polaire permettent de concentrer le flux, on obtient
ainsi une induction dans l’entrefer supérieure à celle de l’aimant, ce qui accroit le couple massique.
Dans cette configuration, l’entrefer est variable em  eM (donc la perméance du circuit magnétique, vu
du stator dépend de la position du rotor (machine à pôles saillants).
 Aimantation radiale
Stator (encoches et
Air
enroulements triphasés)
Pièce polaire
Stator
(Circuit magnétique)
Rotor
(Circuit magnétique) Aimant permanent
Fig. I.6 : Machine synchrone à aimants (P=2), avec pièce polaire, Aimantation radiale.
Les pièces polaires sont sur la périphérie des aimants.
I.2.2 PROPRIETES D’AIMANT PERMANENT [18][30]
Les aimants permanents utilisés dans les machines synchrone ont pour fonction principale la création
du flux inducteur. Ils doivent permettre l’obtention d’une puissance massique élevée, ce qui réduit le
volume de la machine. D’autre part une faible sensibilité à la température est également
indispensable, ce qui limite la désaimantation en fonctionnement normal.
Les aimants sont principalement caractérisés par leurs cycles d’hystérésis et plus particulièrement
par la courbe de désaimantation du plan B-H figure (I.7).
UDL – Sidi bel Abbés - 2011 6

17. CHAPITRE : I Généralités sur la machine synchrone à aimants permanents
λm : droite de charge
Fig. I.7 : Courbe de désaimantation d’un matériau pour aimant permanent
Cette courbe donne :
 l’induction rémanente Br, c’est-à-dire l’induction résiduelle en circuit fermé ; c’est une
indication de la puissance potentielle de l’aimant.
 le champ coercitif de l’induction HcB qui est le champ démagnétisant annulant l’induction ; plus
sa valeur est élevée et plus l’aimant est stable.
 le produit d’énergie volumique (BH)max , qui définit la valeur énergétique de l’aimant par unité
de volume.
 les valeurs Hm et Bm du point de fonctionnement optimal M correspondant (BH)max.
L’aimant permanent idéal pour la réalisation des inducteurs de machines synchrones doit présenter
une caractéristique B(H) rectangulaire, avec des valeurs de Br et Hc aussi élevées que possible.
B
Br
Hc H
Fig. I.8 : Caractéristique B(H) de l’aimant permanent idéal
I.2.3 CHOIX D’AIMANTS PERMANENTS UTILISES POUR LA MSAP [9][29]
Le choix des aimants permanents est essentiel puisqu’il intervient pour beaucoup dans le couple
massique d’un actionneur :
 Les alnico sont des alliages à base de fer, d’aluminium et de nickel, avec des additions de cobalt,
cuivre ou de titane.
 Les ferrites sont des composés d’oxyde de fer, de baryum et de strontium.
UDL – Sidi bel Abbés - 2011 7

18. CHAPITRE : I Généralités sur la machine synchrone à aimants permanents
 Les terres rares tels que les Samarium-Cobalt sont beaucoup plus performants et autorisent une
température de fonctionnement élevée (jusqu’à 300°C), mais ils sont très coûteux en raison
notamment de la présence du cobalt dans leur composition.
BT
Terres rares
1.25
1.2
Alnico
0.35
Ferrite
1000 250 150 H KA/m
Fig. I.9 : Caractéristiques des aimants permanents
Les alliages métaux de transitions-terres rares sont à l’heure actuelle les aimants permanents les
plus performants qui entrent dans la composition des inducteurs des machines synchrones. La version la
plus courante est l’alliage samarium–cobalt Sm2 Co17 , qui est quasiment amagnétiques (la perméabilité
relative vaut environ : µr =1.07) et qui est caractérisé par une induction rémanente et un champ
coercitif élevés (Br =1.25 T,Hc = 1000KA/m).la densité d’énergie emmagasinée dans l’aimant est à
taille égale trois fois plus importante que pour les alnico , et six fois plus importante que pour les
ferrites.
Le choix des aimants permanents dépend des facteurs suivants [18] :
 Performance du moteur.
 Poids du moteur.
 Dimension du moteur.
 Rendement du moteur.
 Facteur économique.
I.3 AVANTAGE DES MACHINES SYNCHRONES A AIMANTS PERMANENTS [1][18][19]
Lors de construction des machines synchrones à aimants permanents (MSAP), l’utilisation des aimants
permanents a la place des bobinages d’excitation offrent beaucoup d’avantage :
 suppression de l’alimentation du rotor (absence du contact bagues balais).
 Moins des pertes de cuivre, les pertes viennent surtout du stator.
 Facteur de puissance et rendement du moteur est améliorées.
 Une faible inertie et un couple massique élevé.
 Une meilleure performance dynamique.
 Construction et maintenance plus simple.
 pas d’échauffement au rotor, et absence des pertes joules.
UDL – Sidi bel Abbés - 2011 8

19. CHAPITRE : I Généralités sur la machine synchrone à aimants permanents
I.4 DOMAINE D’APPLICATION [15]
La machine synchrone à aimants permanents est utilisée dans une large gamme de puissance, allant
de centaines de Watts (servomoteur) à plusieurs méga Watts (système de propulsion des navires), dans
des applications aussi diverse que le positionnement, la synchronisation l’entrainement à vitesse
variable, et la traction :
- il fonctionne comme compensateur synchrone.
- il est utilisé pour les entrainements qui nécessitent une vitesse de rotation constante, tels que les
grands ventilateurs, les compresseurs et les pompes centrifuges, et grâce au développement de
l’électronique de puissance, l’association machine à aimants convertisseur de puissance a trouvé de
nombreuses applications dans les domaines très divers tels que la robotique, la technologie de l’espace
et dans d’autres applications plus particulières (domestique,...).
I.5 CONCLUSION
Une simple comparaison des machines synchrones à aimants permanents avec les autres types de
machines laisse deviner un avenir brillant pour la machine à aimants surtout avec l'apparition des
aimants très performants.
On a présenté dans ce chapitre la machine synchrone à aimants permanents, sa constitution
fondamentale (partie induit et partie inducteur) et puisque nous pouvons distinguer les différents types
de machines synchrones à aimants permanents par la structure de leur rotor, on a analysée ces
structures en présence de pièce polaire et sans pièce polaire avec aimantation radiale et tangentielle.
Ainsi on a mis en évidences les avantages, et les domaines d’application de la machine synchrone à
aimants permanents. ..
UDL – Sidi bel Abbés - 2011 9

20. CHAPITRE II
Modélisation de l’ensemble
convertisseurs-MSAP

21. Chapitre : II Modélisation de l’ensemble convertisseurs-MSAP
II .1 INTRODUCTION
L’étude du comportement d’un moteur électrique est une tache difficile et qui nécessite avant tout
un modèle mathématique. La mise sous forme d’un modèle mathématique d’une MSAP permet
d’observer et d’analyse les différentes évolutions des grandeurs électriques de la MSAP d’une part et
l’élaboration des lois de commande d’autre part [15][17].
Pour commander une machine électrique donnée, il est nécessaire d’utiliser son modèle
mathématique en tenant compte de certaines hypothèses simplificatrices. Du point de vue
mathématique, la machine synchrone présente un système complexe multi variable et non linéaire.
L'approche actuelle de modélisation des machines électriques est basée sur la théorie des deux axes
qui transforme un système triphasé en un système biphasé équivalent, ce qui réduit la complexité du
modèle et permet l'étude des régimes transitoires.
Dans ce chapitre, on présentera la modélisation d’une machine synchrone à aimants permanents sans
amortisseur associée à un convertisseur statique (un onduleur à MLI) et en termine avec les résultats de
simulation de la machine-onduleur.
II.2 HYPOTHESES SIMPLIFICATRICES [1][14][15]
Avant d'établir le modèle mathématique nous devons nous imposer quelques hypothèses :
 L’entrefer est d’épaisseur uniforme, et d’encochage négligeable.
 La saturation du circuit magnétique, l’hystérésis et les courants de Foucault sont négligeables.
 Les résistances des enroulements ne varient pas avec la température et l’effet de peau est
négligeable.
 Le moteur possède une armature symétrique non saturée, les inductances propre et mutuelle
sont indépendants des courants qui circulent dans les différents enroulements.
 La distribution des forces électromotrices, le long de l’entrefer, est supposée sinusoïdale.
 Les pertes fer et l’effet amortisseur sont négligés.
 La perméabilité des aimants est considérée comme voisine de celle de l’air.
II .3 MODELISATION DE LA MSAP [17]
II.3.1 MISE EN EQUATION DE LA MSAP EN TRIPHASE (MODELE EN ABC)
II.3.1.a Equation électrique
Les tensions, flux et courants statoriques triphasés, sont écrits avec les notations vectorielles
suivantes respectivement : vs ,  φ s] et  i s .
La figure (II.1) donne la représentation des enroulements pour une machine synchrone triphasée à
aimants permanents :
UDL - Sidi bel Abbes - 2011 10

22. Chapitre : II Modélisation de l’ensemble convertisseurs-MSAP
Fig. II.1 : Représentation d’une machine synchrone à aimants permanents
dans le repère triphasé
A partir de la figure, nous écrivons les équations de la machine synchrone dans le repère fixe au
stator, en notation matricielle : [15][17]
d φs
[ vs ] = [ Rs ][ is ] +
dt
(2.1)
[φ s ]  [Ls ][is ]  [φ sf ] (2.2.a)
Avec:
[vs ] = [va vb vc ]T : Vecteur tensions statoriques
[is ]  [ia ib ic ]T : Vecteur courants statoriques
[ s ]  [φ a φb φ c ]T : Vecteur flux statoriques
 Rs 0 0
[ Rs ] =  0 Rs 0  : Matrice résistance du stator
 
0
 0 Rs

 La Mab Mac 
[ Lss ] =  Mab Lb Mbc : Matrice inductance du stator
 
 Mac Mbc Lc 
 
 
cos( ) 
 
[φ f ] = φ sf cos(  2 ) : Vecteur flux engendré par l’aimant (2.2.b)
 3 
 4 
cos(  )
 3 
UDL - Sidi bel Abbes - 2011 11

23. Chapitre : II Modélisation de l’ensemble convertisseurs-MSAP
Où :
φ sf : Valeur crête (constante) du flux crée par l’aimant à travers l’enroulement statorique.
 : Angle entre l'axe d et l'axe de référence dans le système triphasé défini par :

 (t) =   d ( ) (2.3)
0
Avec   p  r (2.4)
 : La pulsation électrique.
p : Le nombre de paire de pôles de la machine ;
r : La vitesse de rotation de la machine (rotor).
Le modèle électrique doit être complété par les expressions du couple électromagnétique et de la
vitesse, décrivant ainsi le mode mécanique.
II.3.1.b Equation électromagnétique
La connaissance du couple électromagnétique de la machine est essentielle pour l’étude de la
machine et sa commande.
d[ φ sf ] 
cem  [is ]T  1  d[ Lss ] [is ]  1 

(2.5)
2 d 2 d  
II.3.1.c Equation mécanique
L’équation mécanique de la machine est donnée par :
dr
J  cem  cr  f  r
dt (2.6)
Avec :
Cem : Couple électromagnétique délivré par le moteur.
Cr: Couple résistant.
f : Coefficient de frottement.
J: Moment d’inerte du moteur.
II.3.1.d La puissance absorbée
La puissance absorbée par la machine synchrone à aimants permanents est donnée par l’équation
suivant :
Pa  2    ns  cem (2.7)
Pa : La puissance absorbée par le moteur en (w)
ns : La vitesse du champ tournant en (trs/s)
UDL - Sidi bel Abbes - 2011 12

24. Chapitre : II Modélisation de l’ensemble convertisseurs-MSAP
L’étude analytique du comportement des équations (2.1) et (2.2.a) est relativement laborieuse, vu
le grand nombre de coefficients variables. On utilise alors des transformations mathématiques qui
permettent de décrire le comportement du moteur à l’aide d’équations différentielles à coefficients
constants. L’une de ces transformations est la transformation de Park [17].
II.3.2 MISE EN EQUATION DE LA MSAP EN DIPHASE (MODELE VECTORIEL)
II.3.2.1 principe de la transformation de Park [8][13][17]
Le modèle diphasé de la MSAP s'effectue par une transformation du repère triphasé réel en un
repère diphasé fictive, qui n'est en fait qu'un changement de base sur les grandeurs physiques
(tensions, flux, et courants), il conduit à des relations indépendantes de l'angle θ et à la réduction
d'ordre des équations de la machine. La transformation la plus connue par les électrotechniciens est
celle de Park.
Le repère (d,q) peut être fixé au stator, au rotor ou au champ tournant, Selon l’objectif de
l’application.
La figure (II.2) présente la MSAP en modèle vectoriel (modèle de Park) :
Le repère (oa) est fixe. Le repère (d,q) tourne avec la vitesse de synchronisme  r .
Fig. II.2 : Schéma équivalent de la MSAP dans le repère (d,q)
a) Passage direct : triphasé au diphasé
L’équation qui traduit le passage du système triphasé au système biphasé (d,q) est donnée par :
[ Xdqo]  p( )  [ Xabc]T (2.8)
Avec : P(  ) : la matrice de passage direct de Park .
 2π 4π 
 cosθ cos(θ ) cos(θ )
2 3 3 
P(  ) = =  2π 4π  (2.9)
3  sinθ  sin(θ )  sin(θ )
 3 3 
 1 1 1 

 2 2 2 

UDL - Sidi bel Abbes - 2011 13

25. Chapitre : II Modélisation de l’ensemble convertisseurs-MSAP
Où, X représente les variables considérées de la machine qui sont tensions, courants ou flux.
[Vdqo]  p( )  [Vabc]T (2.10)
[ Idqo]  p( )  [ Iabc]T (2.11)
[dqo]  p( )  [abc]T (2.12)
Xo : La composante homopolaire, ajoutée pour rendre la transformation réversible, elle est nulle
lorsque le système est en équilibre.
B) Passage inverse : diphasé au triphasé
La transformée de Park inverse est nécessaire pour revenir aux grandeurs triphasées, elle est définie
par :
[X abc] = P(  )-1[X dqo] (2.13)
Et la matrice de passage inverse de park P-1(  ) est donnée par :
 1 
 cosθ - sinθ
2
2  
P-1(  ) =  2π 2π 1  (2.14)
3 cos(θ  3 ) - sin(θ  3 ) 2
 4π 4π 1 
cos(θ  ) - sin(θ  ) 
 3 3 2
II.3.2.2 principe de la transformation de CONCORDIA
La transformation direct de CONCORDIA est déterminée par une matrice [c], elle correspond les
vecteurs des axes (a,b,c) aux vecteurs des axes ( ,  ,o ) ,elle est appliquée aux tensions, aux
     
courants, et aux flux, Vabc  , I abc  , abc  aux Vαβo , I αβo , αβo respectivement.
Le vecteur X0 , représente la composante homopolaire.
a) Passage direct : triphasé au diphasé
Si on pose  = 0 dans les équations (2.9) et (2.14), les matrices de PARK deviennent les matrices de
CONCORDIA :
 X   Xa 
 X  = [c]  Xb  (2.15)
   
 Xo   Xc 
Avec :
X  , X  : représentent les vecteurs diphasés qui correspondent aux vecteurs Xa, Xb et Xc .
[C] : la Matrice direct de CONCORDIA, donnée par (2.16) :
UDL - Sidi bel Abbes - 2011 14

26. Chapitre : II Modélisation de l’ensemble convertisseurs-MSAP
 1 1 
 1  
2 2 
2  
[C] =  0
3

3 (2.16)
3  2 2 
 1 1 1 
 

 2 2 2 

B) Passage inverse : diphasé au triphasé
Le passage inverse de la transformation de CONCORDIA est définit par les relations suivants :
 Xa   X 
 Xb  = [c]-1  X  (2.17)
   
 Xc   Xo 
Avec : [c-1] : la Matrice inverse de CONCORDIA .
 1 
-1 2  1 0
2
[c ] =   (2.18)
3 - 1 3 1 
 2 2 2
 
 1 
3 1 
 2
 2 2

On a choisi le coefficient pour les matrices de PARK et CONCORDIA afin de conserver la puissance
pendant le passage entre les deux référentiels.
II.3.2.3 passage du repère ( d, q ) au repère (  ,  )
Le passage des composantes (  ,  ) aux composantes ( d, q ) est donné par une matrice de rotation
exprimée par :
 X   Xd 
 X  = [R]  Xq  (2.19)
   
Avec :
cos   sin  
[R] =  (2.20)
 sin  cos   
[R] : Matrice de passage ( d, q ) au (  ,  )
II.3.3 MODELISATION DE LA MSAP DANS LE REPERE DE PARK
II.3.3.a Equations électriques
Le modèle de la machine après la transformation de Park est donné par :
 dφd
 Vd  R S I d  - pωr φq
dt
 dφq (2.21)
Vq  R S I q   pωr φd
 dt
UDL - Sidi bel Abbes - 2011 15

27. Chapitre : II Modélisation de l’ensemble convertisseurs-MSAP
D’après la relation (2.21), on a le couplage entre les axes « d » et « q » .
Expressions des flux
 φ d  Ld I d  φsf
 (2.22)
φ q  Lq I q
Ld , Lq : Inductances d`axes directe et en quadrature.
II.3.3.B Equation électromagnétique
Le couple électromagnétique Ce dans le référentiel (d, q) est donné par l’expression suivante:
Cem  p  [(Ld - Lq )Id  Iq   sf  Iq] (2.23)
II.3.3.C Equations mécaniques
L'équation mécanique développée par la machine est donnée par la relation suivante :
dr
J  f  r  cem  cr (2.24)
dt
J : Moment d'inertie de la partie tournante (kg.m2).
f : Coefficient de frottement visqueux (N.m.s/rad).
cr : Couple résistant (N.m).
r : Vitesse mécanique (rad/s).
II.3.4 MISE SOUS FORME D’EQUATION D’ETAT
Considérons les tensions (Vd,Vq) et le flux d’excitation sf comme grandeurs de commande, les
courants statoriques (Id, Iq) comme variables d’état. A partir des équations (2.21), (2.22), on peut écrire
le système d’équations comme suit : [14][17]
d[ X ]
 [A][X] + [B][U] (2.25)
dt
1 
 Rs Lq   0 0 
Id    Ld p r  Id  Ld  Vd 
d  Ld     0 0  Vq 
1
 (2.26)
dt  Iq   p Ld
  Rs   Iq    
   Lq

r
Lq Lq     sf 
 
0 0 p r
 Lq 
Avec :
d[ X ]
: Vecteur de dynamique du système.
dt
UDL - Sidi bel Abbes - 2011 16

28. Chapitre : II Modélisation de l’ensemble convertisseurs-MSAP
[A] : matrice d’état.
[ X ] : vecteur d’état (posons [ X ]  [ Id Iq ]T )
[B] : matrice d’entrée
[U] : vecteur de commande (posons [U]  [ vd vq sf] )
T
A partir de (2.23), (2.24) et (2.26), le modèle de le MSAP dans le repère de Park est schématisé par
la figure (II.3) :
r
Fig. II.3 : Modèle de la machine dans le repère de Park.
II.4 MODELISATION DE CONVERTISSEUR
La machine synchrone à aimants permanents est un dispositif à vitesse variable, ou la fréquence des
tensions ou des courants d’alimentation est délivrée par un convertisseur statique et asservi à la
position du rotor.
La structure du convertisseur statique qui alimente la machine est constituée essentiellement, d'un
pont redresseur (AC/DC) connecté au réseau, après redressement, la tension continue est filtrée par
des composants passifs « C » ou « LC », pour être finalement appliquée à l’onduleur, et l’onduleur qui
permet d’alimenter la machine par un système de tension alternatif à fréquence variable. [13]
Schéma de principe de l’association convertisseur –machine est donnée par la figure suivante :
UDL - Sidi bel Abbes - 2011 17

29. Chapitre : II Modélisation de l’ensemble convertisseurs-MSAP
Fig. II.4 : Schéma de principe de l’association convertisseur –machine.
II.4.1 MODELISATION DU REDRESSEUR
Le redresseur est un convertisseur « alternatif/continu ». Il est représenté par la figure
(II.5), La conversion d’énergie électrique permet de disposer une source de courant continu a partir
d’une source alternative.
Fig. II.5 : Représentation de Redresseur à diodes.
Ce redresseur comporte trois diodes (D1, D2, D3). cathode commune assurant l’allée du courant Id, et
trois diodes (D’1, D’2, D’3) a anode commune assurant le retour du courant Id .
II.4.2 MODELISATION DU FILTRE
Pour éliminer les hautes fréquences et pour diminuer les ondulations à la sortie du redresseur nous
insérons à l’entrée de l’onduleur un filtre « LC », celui-ci est schématisé par la figure (II.6).
Fig. II.6 : Représentation d’un filtre “Lc”
UDL - Sidi bel Abbes - 2011 18

30. Chapitre : II Modélisation de l’ensemble convertisseurs-MSAP
II.4.3 MODELISATION DE L'ONDULEUR
L’onduleur de nos jours très largement utilisés dans les systèmes d'entraînement industriels , En
premier lieu, les progrès en matière de semi-conducteur ont permis la réalisation de convertisseurs
statiques de plus en plus performants. En second lieu, l'évolution des techniques numériques et
commandes.
On distingue plusieurs types d’onduleurs :
 Selon la source :
— onduleurs de tension.
— onduleurs de courant .
 Selon le nombre de phases (monophasé, triphasé, etc.),
 Selon le nombre de niveaux (2,3, etc.) [15].
II.4.3.1 Définition de l’onduleur de tension
L’onduleur de tension assure la conversion de l’énergie continue vers l’alternatif (DC/AC). Cette
application est très répandue dans le monde de la conversion d’énergie électrique d’aujourd’hui.
L’onduleur peut être utilisé à fréquence fixe, par exemple alimenter un système alternatif à partir
d’une batterie, ou à fréquence (MLI) variable pour la variation de vitesse des machines électriques.
L’onduleur de tension à MLI permet d’imposer à la machine des ondes de tensions à amplitudes et
fréquences variables à partir du réseau.
L'onduleur qui est connecté à la machine, est constitué de trois bras formé d'interrupteurs
électroniques choisis essentiellement selon la puissance et la fréquence de travail, chaque bras compte
deux composants de puissance complémentaires munis de diode montée en anti-parallèle. Les diodes de
roue libres assurent la continuité du courant dans la Machine une fois les interrupteurs sont ouverts[13].
II.4.3.2 Modélisation de l’onduleur de tension
L’onduleur de tension alimente la MSAP peut être idéalement représenté selon la Figure (II.7):
Fig. II.7 : Schéma de l’association MSAP-onduleur de tension.
Ti et T’i avec i = (a, b, c) sont des transistors MOSFET.
Si et S i ' sont les commandes logiques qui leur sont associées telle que :
 si Si = 1, l’interrupteur Ti est passant et T’i est ouvert.
 si Si = 0, l’interrupteur Ti est ouvert et T’i est passant.
UDL - Sidi bel Abbes - 2011 19

31. Chapitre : II Modélisation de l’ensemble convertisseurs-MSAP
II.4.3.3 Commande de l’onduleur
Pour les commandes de l’onduleur, il existe plusieurs stratégies, parmi les stratégies qu’on a :
 La commande des régulateurs de courant qui génèrent directement les signaux de commande
de l’onduleur : c’est la stratégie ON/OFF(hystérésis).
 La commande des régulateurs de courants qui fournissent des références de tension à
appliquer par l’onduleur et son système de commande par MLI (Modulation de Largeur et
d’Impulsion).
a) Principe de la commande MLI
Dans notre travaille, l’onduleur est commandé par la technique (MLI) générée par une porteuse sous
forme de dent de scie, La technique MLI appelée en anglais (Pulse Wit Modulation PWM). Elle est
utilisée pour générer un signal qui contrôle les interrupteurs, la MLI délivre un signal de commande en
créneaux, il est générer par l’intersection de deux signaux, signal de référence, généralement
sinusoïdale qui est de basse fréquence, et le signal de porteuse qui est de haute fréquence de forme
généralement triangulaire d’où l’appellation triangulo-sinusoïdale .
b) Caractéristique de la MLI
Deux paramètres caractérisent cette commande:
fp
1) m  (2.28)
fr
Vr
2) r (2.29)
Vp
Avec :
 « m » : L’indice de modulation qui définit le rapport entre la fréquence fp de la porteuse et la
fréquence fr de la référence
 « r » : Le taux de modulation (ou coefficient de réglage) qui donne le rapport de l’amplitude de
la modulante Vr à la valeur crête Vp de la porteuse
Fig. II.8 : Principe de la commande MLI-ST
UDL - Sidi bel Abbes - 2011 20

32. Chapitre : II Modélisation de l’ensemble convertisseurs-MSAP
On considère l’alimentation de l’onduleur comme une source parfaite, supposée être constituée par
E
deux générateurs de f.e.m. égale à connectés entre eux par un point commun (0).
2
E/2
K1 K2 K3
VaN
0
VbN
VcN
K 1’ K 2’ K3’
-E/2
Sa Sb Sc
MLI MLI MLI
Porteuse
ua
ub
uc
Fig. II.9 : Schéma équivalent de l’onduleur à MLI
Les tensions aux bornes de l’onduleur :
Vab  Vao - Vbo

Vbc  Vbo - Vco (2.30)
Vca  Vco - Vao

Les tensions VaN , VbN et VcN forment un système de tension triphasées équilibrées, donc :
VaN  VbN  VcN  0 (2.31)
Va N = Va0 + V0N 
 
VbN = Vb0 + V0N  VaN  VbN  VcN  3VoN  Va0  Vb0  Vc0  0 (2.32)

Vc N = Vc0 + V0N 
De (2.32) on déduit :
1
VaN  (Va0  Vb0  Vc0) (2.33)
3
A partir de l’équation (2.32) et (2.33) ,on a :
Vao  2 - 1 - 1  VaN 
Vbo = 1   1 2 - 1 VbN  (2.34)
  3   
Vco 
    1 - 1 2  VcN 
  
UDL - Sidi bel Abbes - 2011 21

33. Chapitre : II Modélisation de l’ensemble convertisseurs-MSAP
Dans une branche d’onduleur, un interrupteur statique (k) peut prendre la valeur +1 ou -1 selon les
conditions suivantes :
Va ref ≥ Vp  Sa = 1 sinon Sa = -1
Vb ref ≥ Vp  Sb = 1 sinon Sb = -1
Vc ref ≥ Vp  Sc = 1 sinon Sc = -1
Avec :
V ref : amplitude de référence.
Vp : amplitude de porteuse.
Et les branches Vko peuvent être exprimées en fonction des switchs « sk » par :
E
Vko = Sk . ( ) Avec : k = (a, b, c) (2.35)
2
Donc :
VaN   2 - 1 - 1  Sa 
VbN   E   1 2 - 1  Sb  : matrice de connexion (2.36)
  6   
VcN 
   1 - 1 2   Sc 
  
Donc, le modèle de l’onduleur est donné par la figure (II.10).
Fig. II.10 : Schéma de l’onduleur sure simulink
II.5 SIMULATION NUMERIQUE
La figure (II.11) Représente l’association onduleur MLI-ST avec MSAP ou les tensions de référence
  
sinusoïdale va, vb, vc sont comparées au signal de la porteuse Vp (dent de scie) afin de déduire les
instants de commutation des interrupteurs.
r
Idq
Cem
Fig. II.11 : Association onduleur (MLI-ST)-MSAP
UDL - Sidi bel Abbes - 2011 22

34. Chapitre : II Modélisation de l’ensemble convertisseurs-MSAP
La figure (II.12) Représente les résultats de la simulation de la machine avec l’onduleur.
La simulation a été effectuée sous le logiciel MATLAB/simulink traitant le comportement d’une
machine synchrone à aimants permanents. A noté que les paramètres de la machine sont donnés en
annexe.
II.5.1 RESULTATS DE SIMULATIONS
16
100
14
couple éléctromagnetique cem (Nm)
80 12
la vitesse Wr (rad/s)
10
60
8
40 6
4
20
2
0
0 0 0.2 0.4 0.6 0.8
0 0.2 0.4 0.6 0.8
temps(s) temps(s)
40
couple réséstante Cr (Nm)
35 courant statorique (A)
2
30
1.5 25
20
1 Iq
15
Id
10
0.5
5
0
0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0 0.2 0.4 0.6 0.8
temps(s) temps(s)
tension de phase va (v) 40
300
30 courant is (A)
200 20
100 10
0 0
-10
-100
-20
-200
-30
-300
-40
0 0.05 0.1 0.15 0.2 0 0.2 0.4 0.6 0.8
temps(s) temps(s)
Fig. II.12 : comportement de l’ensemble onduleur -MSAP avec application de la charge
Cr = 2 (Nm) entre [0.3 0.5](s)
UDL - Sidi bel Abbes - 2011 23

35. Chapitre : II Modélisation de l’ensemble convertisseurs-MSAP
II.5 .2 INTERPRETATION DES RESULTATS
Les résultats de simulation donnés par la figure (II.12), représente la réponse des variables
fondamentales de la machine synchrone à aimants permanents à savoir la vitesse  r , le couple
Electromagnétique Cem et les courants (Id,Iq).
L'allure de la courbe du couple présente au démarrage un pique qui sert à entrainer l’inertie de la
machine pendant le régime transitoire, une fois le régime permanent atteint, le couple revient à zéro.
Lors de l’application de la charge, la machine développe un couple électromagnétique pour
compenser cette sollicitation qui explique l’augmentation de couple dans cette plage qui se traduit par
une diminution de la vitesse.
Pour les courants Id et Iq au début de démarrage on voit des pics de courant assez important et cela
s'explique par la f.e.m qui est due à une faible vitesse de démarrage, ensuite ils se stabilisent à leurs
valeurs nominales r  100 (rad/sec) après un temps assez court.
Les courbes des courants Id et Iq montre bien qui il existe un couplage entre ces variables indiquant
le caractère non linéaire de la machine.
Cette modélisation montre un fortement couplage entre les deux composantes du courant et le
couple. Il est donc nécessaire de trouver un moyen pour rendre leur contrôle indépendant en vue
d’améliorer les performances en régimes dynamiques.
II.6 CONCLUSION
Dans les applications d’entrainement à vitesse variable, il est nécéssaire de modéliser
convenablement tout l’ensemble du système.
Dans ce chapitre, Nous avons modélisé les differents élements du système (convertisseur,MSAP),par
ce que cette partie est nécessaire pour l’intégration de la MSAP dans les systèmes de commandes. Le
modèle mathématique de la MSAP est obtenu dans le repère de park moyennant des hypothèses
simplificatrices pour avoir des équations considérablement simplifiés pour nous permettent d'aborder
aisément la commande qui est présenté dans le chapitre suivants.
Est en fin nous avons présenté le modele du MSAP avec l’onduleur de tension commandé par la
technique MLI-ST et on a conclu que les deux composantes du courant et le couple sont fortement
couplée, Il est donc nécessaire de trouver une moyenne pour rendre leur contrôle indépendant en vue
d’améliorer les performances en régimes dynamiques. c’est pour cette raison, qu’il faut faire un
découplage entre ces variables pour que la machine repond aux éxigences des systemes d’entrainement
à vitesse variables et avoir des hautes performanes dans le regime dynamique.
La solution la plus adéquate actuellement est l’orientation du flux suivant l’axe « d » .Le chapitre
suivant sera consacré à cette technique.
UDL - Sidi bel Abbes - 2011 24

36. CHAPITRE III
Commande vectorielle de la MSAP

37. CHAPITRE : III Commande vectorielle de la MSAP
III.1 INTRODUCTION
La commande des moteurs à courant alternatif est de plus en plus utilisée dans les applications
industrielles. Grâce aux développements des semi-conducteurs de puissance; les moteurs synchrones
à aimants permanents(MSAP) sont capables de concurrencer les moteurs à courant continu dans la
variation de vitesse, car la commutation est réalisée électriquement et à l'extérieur du moteur.
Les nouvelles applications industrielles nécessitent des variateurs de vitesse ayant des hautes
Performances dynamiques. Ces dernières années plusieurs techniques ont été développées pour
permettre aux variateurs synchrones à aimants permanents d’atteindre ces performances.
En 1971, BLASCHKE et HASS ont proposé une nouvelle théorie de commande par orientation du
champ où le vecteur courant statorique sera décomposé en deux composantes l’une assure le contrôle
du flux et l’autre agit sur le couple et rendre sa dynamique identique à celle de la machine à courant
continu a excitation séparée [4][28].
Cette technique est connue sous le nom de la commande vectorielle.
Apres avoir étudié la modélisation de la machine synchrone à aimants permanents (MSAP) et suite a
sa simulation, nous présentons dans ce chapitre la commande vectorielle de la MSAP alimentée par un
onduleur de tension. La stratégie de commande de l’onduleur est contrôlée par la technique MLI, La
simulation est réalisée grâce au logiciel MATLAB/Simulink.
III.2 PRINCIPE DE LA COMMANDE VECTORIELLE
En analysant le système d’équations (2.23) l’équation du couple, nous pouvons relever que le modèle
est non linéaire et il est couplé. En effet, le couple électromagnétique dépend à la fois des grandeurs
I d et I q .
L’objectif de la commande vectorielle de la MSAP est d’aboutir à un modèle équivalent à celui d’une
machine à courant continu à excitation séparée, c’est à dire un modèle linéaire et découplé, ce qui
permet d’améliorer son comportement dynamique[17].
plusieurs stratégies existent pour la commande vectorielle des machines à aimants permanents, la
commande par flux orienté est une expression qui apparait de nos jours dans la littérature traitent les
techniques de contrôle des moteurs électriques, cette stratégie consiste a maintenir le flux de réaction
d’induit en quadrature avec le flux rotorique produit par le système d’excitation comme cela est le cas
dans une machine a courant continue.
Puisque le principal flux de la MSAP est généré par les aimants du rotor, la solution la plus simple
pour une machine synchrone à aimants permanents est de maintenir le courant statorique en
quadrature avec le flux rotorique (le courant direct Id nul et le courant statorique réduire à la seule
composante I q : ( I s  I q ) qui donne un couple maximal contrôlé par une seule composante du courant
( I q )et de réguler la vitesse par le courant traverse I q via la tension V q .Ceci vérifie le principe de la
machine à courant continu.
UDL – Sidi bel Abbés - 2011 25

38. CHAPITRE : III Commande vectorielle de la MSAP
ωr
q
Is=Iq Vd
Vq d
Id=0
f
Is
θ a
0
Fig. III.1 : Principe de la commande vectorielle
Notons aussi que l’annulation de I d provoque une réduction du courant statorique, ce qui permet à
la machine de fonctionner dans la zone de non-saturation.
Pour I d  0 , le système d’équations de la MSAP se réduit aux équations suivantes :
vd   p  r Lq I q

 dI q (3.1)
v q  Rs I  Lq  p r
 q dt f
Cem  p φ f Iq

 d r (3.2)
Cem - Cr  J dt + f.  r

On remarque que cette stratégie permet d’éliminer le problème de couplage entre les axes (d,q)
Lorsque le courant I d est nul ,le modèle de la MSAP est réduit au modèle équivalent à la machine à
courant continu à excitation séparée comme le montre la figure (III.2) :
Cr
Vq 1 Iq - - 1 r
p . f
+
+ Rs  s . L q Cem
J .s  f
-
p.  f
Fig. III.2 : Modèle de MSAP commandé à flux orienté à Id nul
III.3 COMMANDE VECTORIELLE DIRECT PAR COMPENSATION
III.3.1 TECHNIQUES DE DECOUPLAGE
Il existé plusieurs techniques de découplage, parmi c’est techniques on a :
 découplage par compensation
 commande vectorielle indirecte (FOC).
 découplages par régulateur
UDL – Sidi bel Abbés - 2011 26

39. CHAPITRE : III Commande vectorielle de la MSAP
Nous exposons par la suite la première technique qui est l’objective de notre commande à étudiée
en mettant l’accent sur les avantages et les inconvénients.
III.3.2 DECOUPLAGE PAR COMPENSATION [17]
L’alimentation en tension est obtenue en imposant les tensions de référence à l’entrée de la
commande de l’onduleur. Ces tensions permettent de définir les rapports cycliques sur les bras de
l’onduleur de manière à ce que les tensions délivrées par cet onduleur aux bornes du stator de la
machine soient les plus proches possible des tensions de référence. Mais, il faut définir des termes de
compensation, car, dans les équations statoriques, il y a des termes de couplage entre les axes d et q.
Les tensions suivant les axes (d,q) peuvent être écrites sous les formes suivantes :
  d Id 
 Vd   Rs I d  L d dt   ω Lq I q (a)
  

(3.3)
 d Iq 
Vq   Rs I q  L q
   ω ( L d I d  φf )
 (b)
  dt 
  p  r (c)


La figure (III.3) représente le couplage entre l’axe « d » et « q » :
Fig. III.3 : Description de couplage
Les tensions Vd et Vq dépendent à la fois des courants sur les axes « d » et « q », on est donc amené à
implanter un découplage. Ce découplage est basé sur l’introduction de termes compensatoires ed et eq.
ed  ω Lq I q
Avec :  (3.4)
e q  ω . (L d I d  φ f )
A partir de l’équation (3.3) et (3.4) :
On a donc :
Vd  Vd1  ed
 (3.5)
Vq  Vq1  eq
Vd1  ( Rs  s  Ld )  I d
Avec  (3.6)
Vq1  ( Rs  s  Lq )  Iq
UDL – Sidi bel Abbés - 2011 27

40. CHAPITRE : III Commande vectorielle de la MSAP
ed  ω Ld I q
Et  (3.4)
e q  ω . (Ld I d  φ f )
On a donc les courants « I d » et « Iq » sont découplés. Le courant I d ne dépend que de Vd1, et Iq
ne dépend que Vq1, a partir de l’équation (3.6) les courant I d et Iq s'écrivent de la façon suivante:
 Vd 1 (a )
 I d  R  sL
 s d
(3.7)
 Vq1
I q  (b)

 Rs  sLq
s : Opérateur de Laplace.
Le principe de régulation consiste à réguler les courants statoriques à partir des grandeurs de
référence (désirées) par les régulateurs classiques. Le schéma de principe de régulation des courants
statoriques est représenté par la figure ci-dessous [18] :
ω Iq
ω .Lq . I q
Id
Idref - -
Régulateur Id Vd1 + Vd
Découplage
Iqref Vq1 + Vq
Régulateur Iq
- +
ω Ld .I d  f 
Iq
ω Id
Fig. III.4 : Principe de découplages par compensation
Vd1 : la tension à la sortie de régulateur de courant « Id ».
Vq1 : la tension à la sortie de régulateur de courant « Iq » .
UDL – Sidi bel Abbés - 2011 28

41. CHAPITRE : III Commande vectorielle de la MSAP
Si on associer la machine avec le bloc de compensation on obtient la figure (III.5) :
- Id
Idref + Vd1
Régulateur Id 1
+ +
- + Rs  sLd
ed ed
Iqref - Vq 1 Iq
+ Vq1
Régulateur Iq + + Rs  sLq
+ -
Régulateur Iq eq
Correction+Découplage eq Modèle de la MSAP
eq
Fig. III.5 : Structure générale : (machine-découplage par compensation).
Les actions sur les axes d et q sont donc découplés et représentées par la figure (III.6) :
-
Idref + Vd1 Id
Régulateur Id 1
Rs  sLd
Iqref + - Vq1 1 Iq
Régulateur Iq Rs  sLq
Régulateur Iq
Fig. III.6 : commande découplée
III.4 DETERMINATION DES REGULATEURS
III.4.1 DESCRIPTION DU SYSTEME GLOBAL
La référence du courant direct I dref est fixée, et la sortie du régulateur de vitesse Iqref constitue la

consigne de couple Cem . Les références des courants I dref et Iqref sont comparées séparément avec
les courants réels de la machine I d et Iq .
Les erreurs sont appliquées à l’entrée des régulateurs classiques de type PI. Un bloc de découplage
 
génère les tensions de références Vd , Vq .
Le système est muni d’une boucle de régulation de vitesse, qui permet de générer la référence de
courant Iqref . Par contre, le courant I dref est imposé nul.
Chaque axe découplé peut être représenté par un bloc de correction Ci(s) avec (i = d, q). La figure
(III.7) représente le schéma global de la commande vectorielle d’une machine synchrone à aimants
permanents avec compensation dans le repère ( d,q ) :
UDL – Sidi bel Abbés - 2011 29

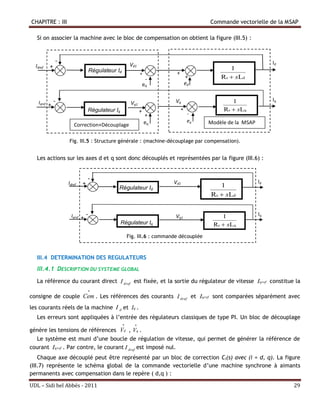
42. CHAPITRE : III Commande vectorielle de la MSAP
Id E
Idref - Vd
2Φ MSAP
Commande
Cd(s)
+
MLI
ω rref Charge
Iqref
reg(ωr) Cq(s)
+ 3Φ ωr
- - Iq
Vq
1 Onduleur
s
P3Φ
Fig. III.7: Schéma bloc de la commande vectorielle avec compensation des f.e.m
III.4.2 CALCUL DES REGULATEURS
Pour calculer les paramètres des régulateurs, on adopte des modèles linéaires continus.
Les méthodes classiques de l’automatique sont utilisables. Ces méthodes ont l’avantage d’être
simples et faciles à mettre en œuvre.
Les éléments fondamentaux pour la réalisation des régulateurs sont les actions P.I.D
(proportionnelle, intégrale, dérivée). Les algorithmes, même les plus performants, sont toujours une
combinaison de ces actions.
Nous considérons que la machine est orientée vectoriellement et complètement découplée. Ceci
nous permet d’écrire les équations de la machine d’une manière simple et de calculer les coefficients
des régulateurs.
Nous nous contentons de régulateurs classiques de type PI dans une structure par boucle imbriquée.
Dans ce cas, nous pouvons distinguer deux modes :
 Le mode électrique (mode rapide : boucle interne).
 Le mode mécanique (mode lent : boucle externe).
Pour chacune des boucles de courant, nous proposons de commander la machine par des régulateurs
classiques Proportionnel Intégrateur (PI) pour compenser la perturbation du couple résistant au niveau
de la réponse de la vitesse de rotation, c'est-à-dire ; ils comportent une action proportionnelle qui sert
à régler la rapidité avec laquelle la régulation doit avoir lieu et une action intégrale qui sert à éliminer
l’erreur statique entre la grandeur régulée et la grandeur de consigne. [4][17].
Le régulateur PI (action proportionnelle-intégrale) est une combinaison d'un régulateur P et d'un
régulateur I.
Le régulateur (PI) est la mise en parallèle des actions proportionnelle et intégrale, figure (III-9).
UDL – Sidi bel Abbés - 2011 30

43. CHAPITRE : III Commande vectorielle de la MSAP
La relation entre la sortie u (t ) et le signal d’erreur  (t ) est donnée par la relation suivante :
r
t
ur (t )  kp (t )  ki   (t )d (t ) (3.8)
0
ur ( p ) ki (3.9)
C’est à dire :  kp 
 ( p) p
kp : Gain proportionnel
ki : Gain intégral
1
Ti : Constant de temps d’intégration; avec Ti 
ki
Le régulateur PI est donné par la figure suivante :
Kp + y
Yref  Ur
Système
+ 1
- Ki +
s Cr
P.I
Fig. III.9 : Régulateur PI
La fonction de transfert sera :
Ki
Ur  ( K p  ) (3.10)
s
On peut aussi écrire le régulateur sous la forme suivante :
U r 1  sT1 (3.11)
P.I  
 sT2
 kp  T 1 (a)
 T2
Avec :  1 (3.12)
 ki  T 2
 (b)
III.4.3 DIMENSIONNEMENT DES REGULATEURS
La machine étant découplée selon deux axes (d,q), la régulation sur l'axe "d" est faite par une seule
boucle, tandis que la régulation sur l'axe "q" est faite par deux boucles en cascades l'une interne pour
réguler le courant et l'autre externe pour réguler la vitesse.
.
.
.
UDL – Sidi bel Abbés - 2011 31

44. CHAPITRE : III Commande vectorielle de la MSAP
a-Régulateur du courant « Iq »
La commande de la MSAP s’effectue en contrôlant les courants I d et Iq , le système est composé
d’une boucle de régulation de vitesse, qui impose la référence Iqref , le courant Id est maintenu nul,
la commande est effectuée par les régulateurs PI pour avoir l’erreur statique nulle (  = 0).
vq1
Sachant que Iq = 3.7(b)
Rs  s.Lq
1  sT 1
Et que la forme générale du régulateur PI est : (équation (3.11)), on aboutit au schéma de
sT 2
la figure (III.10) :
Iq ref +  Iq 1  sT1q Vq1 1
Iq
sT2q R  sLq
-
Fig. III.10 : Boucle de régulation du courant Iq
La fonction de Transfer en boucle ouvert (FTBO) de la figure (III-10) est :
1  sT 1q
………………..
(3.13)
FTBO=
sT 2 q( Rs  sLq )
1  sT 1q (3.14)
FTBO =
sT 2 qR(1  s Lq )
Rs
Par l’utilisation de la méthode de compensation des pôles, on aura :
1  sT 1q  1  s Lq Ce qui se traduit par la condition:
Rs
Lq  T 1q  q (3.15)
Rs
Avec Lq : constant de temps électrique.
Rs
Si en remplace la constant T 1q par sa valeur équation (3.15) dans l’équation (3.13), on trouve :
1
FTBO = (3.16)
sRsT 2 q
Pour la fonction de Transfer en boucle fermé(FTBF) :
FTBO
FTBF=
1  FTBO (3.17)
1  1 
FTBF= de la forme   (3.18)
1  sRsT 2 q  1  s  q
UDL – Sidi bel Abbés - 2011 32

45. CHAPITRE : III Commande vectorielle de la MSAP
Par identifications on trouve :
q
q  RsT 2 q  T 2 q  (3.19)
Rs
On imposant le temps de référence : Tr  3q (critère de  5%) (3.20)
Tr
On a : T 2q  (3.21)
3Rs
Tr : Temps de réponse imposé.
 q  Lq : Constante de temps électrique de l'axe "q" du machine.
Rs
Rs
En remplace l’équation (3.19) dans (3.12b), On obtient : Ki  (3.22)
q
Si on remplace l’équation (3.20) dans (3.22) :
kpq  3Lq
 Tr (3.23)
On obtient finalement  3Rs
 kiq  Tr

b-Régulateur du courant « Id »
La boucle de régulation sur l’axe « d » est présentée par la figure suivant :
Idref +  Id 1  sT1d
Vd 1 1 Id
sT2d R  sLd
-
Fig. III.11 : Boucle de régulation du courant Id
Pour la régulation du courant Id , on suit la même procédure utilisée pour la régulation du courant Iq .
1  s.T 1d
FTBO = (3.24)
Ld
s.T 2 d . Rs(1  s )
Rs
1
FTBF = (3.25)
1  sRsT 2 d
Ld (3.26)
 T 1d  d
Rs
(3.27)
On impose : Tr  3d
UDL – Sidi bel Abbés - 2011 33

46. CHAPITRE : III Commande vectorielle de la MSAP
d (3.28)
d  R.T 2d  T 2 d 
Rs
On remplace l’équation (3.26) dans (3.27) on obtient :
Tr (3.29)
T 2d 
3Rs
 d  Ld : Constante de temps électrique de l'axe "d" du machine.
Rs
c- Régulation de vitesse
Le processus à commander est décomposé en deux sous système :
 Sous système du réglage de courant Iq donc du couple aussi.
 Sous système de la partie mécanique.
La boucle de régulation de la vitesse est représentée par la figure ci-dessous :
Cr
-
*
Iq Iq Cem+
* 1 r
* k
 i
1 p. f
r + -
k p 1  qs Js  f
s -
ki
k p  p. f
s
Fig. III.12.a : Boucle de régulation de vitesse
Le schéma de la figure (III.12.a) peut être simplifié par la figure (III.12.b) :
*
wr F Fo
+ -
Fig. III.12.Boucle de régulation de vitesse
F (s ) : La fonction de transfert du régulateur de vitesse.
ki 1  sT 1 (3.30)
F ( s )  k p  
s sT 2
kp  T1
 T2
Ou :  1 (3.31)
 ki  T2

UDL – Sidi bel Abbés - 2011 34

47. CHAPITRE : III Commande vectorielle de la MSAP
Fo (s)  : La fonction de transfert en boucle ouverte :
p f
Fo ( s )  (3.32)
f (1  s q )  (1  s m )
J
m  : Constant mécanique de la machine.
f
La FTBF est donnée par :
F ( s ) Fo ( s )
FBF ( s )  (3.33)
1  F ( s ) Fo ( s )
Après les calculs en trouve:
p f (k pws  kiw )
FBF ( s )  (3.34)
J  q s  ( J  f  q ) s ²  ( p   f  k pw  f ) s  p f kiw
3
Si on néglige ( J   q ) et ( f   q ) devant (J ) , le polynôme caractéristique de cette fonction devient:
p( s)  Js ²  ( f  p f .k p ) s  p f .ki (3.35)
En imposant au polynôme caractéristique en boucle fermée deux pôles complexes conjugués
S1,2    (1  j ) , il devient alors :
p( S )  s 2  2    s  2   2 (3.36)
Par identification terme à terme entre l’équation (3.35) et (3.36) on trouve :
 2 J  f
 k pw 
 p f
 (3.37)
k  2  J
2
 iw p f

Ou :   wn (3.38)
wn : Pulsation propre du système
 : Facteur d’amortissement
III.5 LIMITATION DES COURANTS [4][11][12]
Les organes de commande introduisent des limitations sur la grandeur de commande [u] .ces
limitations peuvent causer des problèmes lors de grands phénomènes transitoires sous formes d’un
dépassement élevé de la grandeur à régler, voire même d’un comportement instable du réglage.
La caractéristique non linéaire de la limitation ne permet plus l’application de la théorie linéaire
afin d’analyser précisément le comportement dynamique dès que la sortie du régulateur est saturée.
UDL – Sidi bel Abbés - 2011 35

48. CHAPITRE : III Commande vectorielle de la MSAP
La saturation perturbe également le fonctionnement des régulateurs comportant une action
intégrale. En effet, la composante intégrale continue à croitre, bien que la sortie du régulateur soit
limitée.
Cr
wrref + ki  C em - 1 wr
kp  
- s + f  J .s
Fig. III.13 Boucle de régulation de vitesse avec limitation du courant.
Afin d’éviter ces inconvénients, il s’avère indispensable de corriger le comportement dynamique du
régulateur (en particulier la composante intégrale) lorsque la limitation est atteinte. Cette mesure est
appelée mesure anti-reset-windup (anti remise de l’emballement).
Saturation
1 Kp
In1 1
Out1
1
Ki
s
Km
Fig. III.14 : Régulateur PI avec anti_windup
Comme le dimensionnement de ce régulateur est très compliqué, nous procédons par des simulations
pour régler le correcteur de vitesse. La méthode utilisée est du type :
Essai – erreur - dépassement. Les coefficients obtenus sont : k p ki k m .  
III.6 SCHEMA GLOBAL DE SIMULATION
Le schéma de simulation de la commande vectorielle avec association onduleur à deux niveaux et
MSAP est représenté par la figure (III-15) :
Reg(wr)
Régulateur wr
Reg(Iq)
Régulateur Iq
wref Onduleur va wr wr
Découplage
par M
Compensation vb
Idref = 0
-------- S
Reg(Id) Id Transformation Id ,Iq IdIq
Régulateur
dq_abc
A
vc
MLI P
Cr
Cem Cem
Cr
t
Fig. III.15 : Schéma globale de simulation de la commande vectorielle avec réglage classique (PI).
UDL – Sidi bel Abbés - 2011 36

49. CHAPITRE : III Commande vectorielle de la MSAP
III.6.1 RESULTATS DE SIMULATION
150 40
30 Iq(A)
100
20
50
10
vitesse mécanique
réelle wr (rad/s) 0
0
-10
Id(A)
-50
-20
-100 vitesse de référence wr (rad/s) -30
-40
-150
0 0.2 0.4 0.6 0.8 0 0.2 0.4 0.6 0.8
temps(s) temps(s)
40
8
30
couple éléctromagnetique Cem (Nm)
couple
6 résistante 20
Cr=8Nm 10
4 0
-10
2 -20
-30
0
0 0.2 0.4 0.6 0.8 -40
0 0.2 0.4 0.6 0.8
temps(s) temps(s)
40
Is(A)
30
20
10
0
-10
-20
-30
-40
0 0.2 0.4 0.6 0.8
temps(s)
Fig. III.16 : Résultats de simulation de la commande vectorielle du MSAP avec réglage classique (PI).
III.7 INTERPRETATION DES RESULTATS
Les performances de la commande proposée ont été testées par simulation dans le cas du réglage
classique d’une MSAP alimentée par un onduleur de tension à deux niveaux, avec un régulateur PI face
à une vitesse de référence de 100 (rad/s) puis -100 (rad/s) à l’instant t=0.6 (s) suivie d’une application
d’un couple résistante de 8 (Nm) à une période de [0.2s], entre t=0.2 (s) et t=0.4 (s).
UDL – Sidi bel Abbés - 2011 37

50. CHAPITRE : III Commande vectorielle de la MSAP
Les résultats de simulation montrent que le découplage est maintenu quelque soit la variation de la
charge (dans le régime permanent). L’onduleur engendre des fluctuations qui sont ressenties au niveau
du couple.
Le courant I d après le régime transitoire revient à sa valeur zéro.
La variation de la vitesse est rapide avec très petite dépassement et sans erreur statique, le rejet de
perturbation est aussi rapide avec un temps de réponse de 0.022 (s).
III.8 CONCLUSION
L’application de la commande vectorielle à la MSAP nous permet non seulement de simplifier le
modèle de la machine mais aussi améliorer ces performances dynamique et statique, le développement
de la commande vectorielle permet d’atteindre un découplage entre les axes « d » et « q » ce qui rend
la machine synchrone à aimants permanents similaire à la machine à courant continu. Le réglage de la
vitesse par la commande vectorielle avec un régulateur classique (PI) permet d’obtenir des
performances dynamiques satisfaisantes.
Puisque les correcteurs classiques sont dimensionnés à partir des paramètres de la machine. Si ces
derniers varient dans une large plage de fonctionnement, les performances sont détériorées, alors il est
préférable de voir d’autres techniques de réglage. Ainsi notre prochain chapitre sera consacré à la
commande par mode glissant. Où les correcteurs sont connus par leur robustesse.
UDL – Sidi bel Abbés - 2011 38

51. CHAPITRE IV
Commande par mode glissant de la MSAP

52. CHAPITRE : IV Commande par mode glissant de la MSAP
IV-1 INTRODUCTION
Dans le chapitre précédent nous avons mis en œuvre la commande vectorielle en utilisant les
régulateurs PI classiques ou les lois de commande qui utilise les régulateurs à action proportionnelle,
intégrale donnent des bons résultats dans le cas des systèmes linéaires à paramètres constants. [4][22]
Ces lois de commande classique peuvent être insuffisantes car elles sont non robustes surtout lorsque
les exigences sur la précision et autres caractéristiques dynamiques du système sont strictes. On doit
faire appel à des lois de commande insensibles aux perturbations, aux variations de paramètres et aux
non linéarités. [4][26]
Lorsque la partie commandée est soumise à des perturbations et à des variations de paramètres du
système, une solution auto adaptative, qui par réajustement des paramètres des régulateurs, permet
de conserver des performances fixées à l’avance en présence de perturbations et de variations de
paramètres. Cette solution présente l’inconvénient de nécessiter une mise en œuvre souvent complexe.
Ainsi, il est possible d’enregistrer une autre solution plus simple, faisant appel à une classe
particulière de systèmes de commande appelés « systèmes à structures variables », ces systèmes ont
fait l’objet depuis longtemps de travaux importants au Japon par H.Harachima, aux Etat Unis par
I.I.Slotine et en ex-Union Soviétique par V.Utkin et ceci à partir des travaux théoriques du
mathématicien soviétique A.F.Filipov. [21][22]
L’intérêt récent accordé à cette technique de commande est dû essentiellement à la disponibilité
des composants électroniques plus performants et de microprocesseurs très développés.
La commande à structure variable (CSV) est par nature une commande non linéaire. La
caractéristique principale des systèmes à structure variable est que leur loi de commande se modifie
d’une manière discontinue. [5][22][23]
Ce type de commande (CSV) présente plusieurs avantages tels que la robustesse, précision
importante, stabilité et simplicité, temps de réponse très faible vis-à-vis l’insensibilité a la variation
des paramètres internes et externes. Ceci lui permet d'être particulièrement adaptée pour traiter les
systèmes qui ont des modèles mal connus, soit à cause de problèmes d'identifications des paramètres,
soit à cause de simplification sur le modèle du système [4][5][26].
IV-2 GENERALITES SUR LA THEORIE DU CONTROLE PAR MODE GLISSANT
Les commutations de la commande à structure variable s’effectuent en fonction des variables
d’état, utilisées pour créer une « variété » ou « surface » dite de glissement.
La commande par mode glissant consiste à ramener la trajectoire d’état vers la surface de
glissement et de le faire évoluer dessus avec une certaine dynamique jusqu’au point d’équilibre.
Une surface de glissement : c’est une surface S sur laquelle le système suivra l’évolution souhaitée
(sur laquelle évoluera l’erreur) [11].
Quand l’état est maintenu sur cette surface, le système est dit en régime glissant. Ainsi, tant que les
conditions de glissement sont assurées, la dynamique du système reste insensible aux variations des
paramètres du processus, aux erreurs de modélisation (dans une gamme qui reste plus large par rapport
à celle des approches classiques de l’automatique), et à certaines perturbations [4][20].
UDL – Sidi bel Abbés - 2011 39

53. CHAPITRE : IV Commande par mode glissant de la MSAP
IV.3 L’OBJECTIF DE LA COMMANDE PAR MODE GLISSANT
L’objectif de la commande par mode glissant est de :
 synthétiser une surface s( x )  0 , telle que toutes les trajectoires du système obéissent a un
comportement désiré de poursuite, de régulations et de stabilité.
 Déterminer une loi de commande qui est capable d’attirer toutes les trajectoires d’état vers la
surface de glissement s( x )  0 et de les maintenir sur cette surface. [11]
IV.4 PRINCIPE DE LA COMMANDE A STRUCTURE VARIABLE
IV.4.1 DEFINITION DES SYSTEMES NON LINEAIRES
Le comportement des systèmes possédant des discontinuités peut être décrit formellement par
l'équation:
x(t )  f ( x, t,U )
 (4.1)
 x : le vecteur d'état, x   .
n
 t : le temps
 U : grandeur de commande, u   .
m
 f : la fonction décrivant l'évolution du système au cours du temps.
Historiquement, les premiers régulateurs bâtis sur ce modèle ont été de simples relais. Faciles à
mettre en œuvre, ils ont représenté les prémices du contrôle par structure variable. Ils ont ainsi amené
les automaticiens à développer une théorie qui puisse décrire un tel fonctionnement. Les bases d'une
telle théorie ont été posées : il suffit de dire que le comportement du système est décrit par deux
équations différentielles distinctes, suivant que l'équation d'évolution du système soit supérieure ou
inférieure à une surface dénommée hypersurface de commutation où :
U  ( x ) si
 S i ( x )  0,
U ( x)   i  1,.....m (4.2)
U  ( x ) si
 S i ( x )  0,
La commande U est construire de façon à ce que les trajectoires du système soient amenées vers
la surface de glissement et soient ensuite maintenues dans un voisinage de celle-ci.
U  et U étant des fonctions continus.

Le système variable (4.1) avec la loi de commande (4.2) peut se ramener à l’écriture suivante :
 f  ( x, t ) si S ( x, t )  0 (4.3)
x (t )  f ( x, t ,U )   

 f ( x, t ) si S ( x, t )  0
S ( x, t ) : est une surface dans  n qui divise l'espace en deux parties disjointes : S ( x, t )  0 et S ( x, t )  0
.

En dehors de la surface de discontinuité, les fonctions f et f  peuvent avoir différents
comportements :

 les fonctions f et f  traversent la surface d'un côté vers l'autre : Figure (IV.1.a) et
UDL – Sidi bel Abbés - 2011 40

54. CHAPITRE : IV Commande par mode glissant de la MSAP
Figure (IV.1.b).

 les fonctions f et f 
sont pointés chacun vers la surface : Figure (IV.1.c).
Fig. IV.1.a Fig. IV.1.b Fig. IV.1.c
Fig. IV.1 : Différents comportements en dehors de la surface de discontinuité.
 
Le cas qui nous intéresse est celui où les deux fonctions f et f sont pointés chacun vers la
surface, on dit alors que la surface est attractive, figure (IV.1.c). [7]
En se plaçant dans un espace à 2 dimensions, le principe de discontinuité de la commande (Equation
(4.2) et (4.3)) peut être illustré par la figure (IV.2) :
Fig. IV.2 : Convergence de la trajectoire vers la surface de commutation
Grâce à la discontinuité de la commande
Ainsi, le problème de l'existence du régime glissant se résume à analyser la trajectoire du système,
qui ne doit pas s'éloigner de la surface S. Nous cherchons à vérifier que la distance et la dérivée de la
distance (autrement dit, la vitesse d'approche), entre la trajectoire et la surface de commutation
soient opposées en signe, cela peut être exprimé par l'équation suivante :

lim S  0 et 
lim S  0
(4.1)
s 0 s  0
D’où la condition d’attractivité pour l’obtention du régime glissant : (4.5)

S ( x ).S ( x )  0
Il s'agit du principe d'attractivité. Des justifications mathématiques complémentaires, pourront être
trouvées dans les ouvrages traitant des systèmes non linéaires.
UDL – Sidi bel Abbés - 2011 41

55. CHAPITRE : IV Commande par mode glissant de la MSAP
IV.4.2 FORMULATION DES EXPRESSIONS GENERALES DE LA COMMANDE PAR MODE DE GLISSEMENT
Les définitions des modes glissant dans le cadre d’un système non linéaire dont le comportement
dynamique est défini par les équations différentielles suivants :
(4.6)
x  f ( x, t )  g ( x, t )U

Où :
x : le vecteur dont les composantes sont les variables d'état, x  n ;
u : vecteur de commande, u  m .
n 1
f : est un champ de vecteur ou fonction vectorielle, f :    ;
n
n 1
B( x, t ) : la matrice de commande, b( x, t ) :    .
n*m
La fonction de commutation S sépare l'espace d'état en deux régions représentant des structures
différentes. C'est une fonction vectorielle dont les composantes sont des fonctions scalaires
représentatives d'une relation algébrique entre deux grandeurs. Elle est définie par l'utilisateur afin
d'obtenir les performances dynamiques désirées. [4][10][11]
Lorsque nous sommes dans le "mode de glissement", la trajectoire restera sur la surface de
commutation. Cela peut être exprimé par:
S( x , t )  0 et 
S( x , t )  0 (4.7)
IV.4.3 CONDITION POUR L’EXISTENCE DU MODE DE GLISSANT
Le mode de glissement existe lorsque les commutations ont lieu continûment entre U max et U min
pour un système de deuxième ordre avec les grandeurs d’état X S1 et X S 2 , ce phénomène est présenté
par la figure suivante :
Fig. IV.3 : phénomène de glissement
On admet d’abord une hystérèse sur la loi de commande S(x) = 0, par conséquent, les commutations
ont lieu sur les droites décalées parallèlement de ± Δ Sh .
UDL – Sidi bel Abbés - 2011 42

56. CHAPITRE : IV Commande par mode glissant de la MSAP
Une trajectoire avec U  U max touche au point (a) le seuil de basculement inférieur. Si U  U min , la
trajectoire est orientée vers l’intérieur de la zone de l’hystérèse, elle touche au point (b) le seuil de
basculement supérieure ou a lieu une commutation sur U  U min .
Si la trajectoire est de nouveau orientée vers l’intérieur, elle touche le point (c) le seuil de
basculement inférieur et ainsi de suite. Il y a donc un mouvement continu de la zone de l’hystérèse.
On suppose dans le cas idéal que l’hystérèse est infiniment petite. La loi de commutation fait un
mouvement infiniment petit autour de S ( Xs ) 0 . Par conséquent, le vecteur d’état X S suit une
trajectoire qui respecte cette condition. La fréquence de commutation est donc infiniment élevée
[5][12].
IV.5 LES MODES DE LA TRAJECTOIRE DANS LE PLAN DE PHASE
La technique par mode glissement consiste à ramener la trajectoire d’état d’un système vers la
surface de glissement et faire commuter a l’aide d’une logique de commutation appropriée jusqu’au
point d’équilibre.
Cette trajectoire est constituée de trois parties distinctes, figure (IV.4) :
 Le mode de convergence (MC) : dont la variable régulier se déplace à partir du point d’équilibre
initial.
 Le mode glissement (MG) : durant lequel la variable d’état à atteint la surface de glissement.
 Le mode de régime permanent (MRP) : le comportement du système est autour du point
d’équilibre.
Xs2
MC MG
Xs1
MRP
S(X)
Fig. IV.4 : les modes de trajectoires dans le plan de phase
IV.6 CONCEPTION DE LA COMMANDE PAR MODE GLISSANT
La conception de la commande par mode glissant revient principalement à déterminer trois étapes :
1. Le choix de la surface.
2. L’établissement des conditions d’existence de la convergence.
3. La détermination de la loi de commande.
UDL – Sidi bel Abbés - 2011 43

57. CHAPITRE : IV Commande par mode glissant de la MSAP
IV.6.a CHOIX DE LA SURFACE DE GLISSEMENT
Le choix de la surface de glissement concerne non seulement le nombre nécessaire de ces
surfaces mais également leur forme en fonction de l’application et de l’objectif visé .En général,
pour un système défini par l’équation d’état suivant [11] :

x(t )  f ( x, t )  g ( x, t )u(t ) (4.8)
Il faut choisir «m» surfaces de glissement pour un vecteur y de dimension «m» .En ce qui concerne la
forme de la surface, deux possibilités se présentent : soit dans le plan de phase ou dans l’espace
d’état. Dans ce dernier cas, on trouve la méthode dite«loi de commutation par contre réaction d’état»
celle- ci utilise les concepts du réglage par contre réaction d’état pour synthétiser la loi de
commutation. Son inconvénient majeur réside dans le faite qu’elle présente une réponse transitoire
lente et de conception très difficile.
Dans le cas du traitement dans l’espace de phase, la fonction de commutation est une fonction
scalaire, telle que la variable à régler glisse sur cette surface pour atteindre l’origine du plan de
phase.
Ainsi, la surface S (x) représente le comportement dynamique désiré du système. J.J.Slotine
propose une forme d’équation générale pour déterminer la surface de glissement qui assure la
convergence d’une variable vers sa valeur désirée, cette équation est sous la forme suivant : [2]

Avec : S ( x )  (   x ) r 1 e( x ) (4.9a)
t
e(x ) : L’écart de la variable à régler. e( x)  x ref  x . (4.10)
 x : Une constante positive qui interprète la bande passante du contrôle désiré.
r : Degré relatif, égale au nombre de fois qu’il fait dériver la sortie pour faire apparaître la
commande.
Il est à noter qu’en général, on donne une grande valeur à  x pour assurer l’attractivité ainsi que le
maintien du système sur cette surface.
Où : x  k  (4.9b)
e 
k : scalaire positif donné ;
  : Constante positive de valeur très faible.
k
Il est à noter que représente la pente de glissement le long de la surface quand elle est atteinte

par le système.
Pour r 1 S ( x)  e( x) .
Pour r  2 S ( x)  x e( x)  e( x) .

Pour r  3 S ( x)  2 e( x)  2x e( x)  e( x) .
x
 
 S ( x )  0 est une équation différentielle linéaire dont l’unique solution est e( x )  0 .
UDL – Sidi bel Abbés - 2011 44

58. CHAPITRE : IV Commande par mode glissant de la MSAP
La difficulté de cette commande, revient à un problème de poursuite de trajectoire dont l’objectif
est de garder S (x) à zéro .Ceci est équivalent à une linéarisation exacte de l’écart en respectant la
condition de convergence .La linéarisation exacte de l’écart a pour but de forcer la dynamique de
l’écart : (référence – sortie) à être une dynamique d’un système linéaire autonome d’ordre « r »
[11][12][23][28].
S (x)  e r (x) e r 1 ( x ) e(x )
 

e( x ) : Sortie
S ( x ) : Entrée  r 1



0
Fig. IV.5 : Linéarisation exacte de l’écart.
IV.6.b CONDITIONS DE CONVERGENCE [11][12]
Les conditions de convergence ou d’attractivité permettent aux dynamiques du système de
converger vers les surfaces de glissement et rester indépendamment a la perturbation. Il y’a deux
conditions, celles correspondent au mode de convergence de l’état de système qui sont :
 La fonction de commutation.
 La fonction de LYAPUNOV.
IV.6.b.1 Fonction directe de commutation
C’est la première condition de convergence, elle est proposée par U.TKIN, Il s’agit de donner à la
surface une dynamique convergente vers zéro. Elle est donnée par :

S ( x ). S ( x )  0 (4.11)
Ceci signifie, Figure (IV.6) que la trajectoire du point de fonctionnement après avoir atteint la
surface de glissement durant un régime transitoire qui vérifie la condition (4.11) oscille de part et
d’autre de la surface avec une fréquence élevée et une amplitude faible et tend rapidement vers le
point de fonctionnement désiré ( e( x )  0 ).[28]
UDL – Sidi bel Abbés - 2011 45

59. CHAPITRE : IV Commande par mode glissant de la MSAP
Fig. IV.6 : L’évolution du point de fonctionnement dans l’espace des phases
TG: temps de glissement; le glissement s’effectue a partir de TG au voisinage de la surface de
glissement S(x) = 0.
IV.6.b.2 Fonction de LYAPUNOV [24]
La fonction de LYAPUNOV est une fonction scalaire positive V ( x)  0 pour les variables d’état du
système, la loi de commande doit faire décroitre cette fonction, la condition, elle rend la surface
attractive et invariante.
En définissant la fonction de LYAPUNOV par :
1 2
V ( x)  S ( x) (4.12)
2
Pour que la fonction de LYAPONUV décroisse, il suffit de s’assurer que sa dérivée soit
négative. Ceci est vérifié par la relation suivante :
 
V ( x)  0  S ( x)S ( x)  0
(4.13)
Cela peut être exprimé par l'équation suivante :

lim S  0 et 
lim S  0
s  0 s  0
(4.14)
L'équation (4.12) explique que le carré de la distance vers la surface mesurée par S2(x)
diminue tout le temps, contraignant la trajectoire du système à se diriger vers la surface dans les
deux côtés. Cette condition suppose un régime glissant idéal- où la fréquence de
commutation est infinie.
IV.6.C CALCUL LA LOI DE COMMANDE [11]
Une fois la surface de glissement est choisie, ainsi que le critère de convergence, il reste à
déterminer la commande nécessaire pour ramener la variable à contrôler vers la surface et
ensuite vers son point d’équilibre en maintenant la condition d’existence des modes glissants.
UDL – Sidi bel Abbés - 2011 46

60. CHAPITRE : IV Commande par mode glissant de la MSAP
Une des hypothèses essentielles dans la conception des systèmes à structure variable contrôlés par
les modes glissants, est que la commande doit commuter entre u Max et u Min instantanément (fréquence
infinie), en fonction du signe de la surface de glissement Figure (IV.7) .Dans ce cas, des oscillations de
très haute fréquence qui apparaissent dans le mode de glissement.
u
u Max
S (x)
u Min
Fig. IV.7 : Commande appliquée aux systèmes à structure variable.
IV.7 DEFINITION DES GRANDEURS DE COMMANDE [4][11][24][26]
En mode glissant, le but est de forcer la dynamique du système à correspondre avec la surface de
glissement S(X) au moyen d’une commande définie par l’équation suivante :
u(t )  ueq (t )  uN (4.15)
avec :
 U : grandeur de commande,
 U eq : correspond à la composante équivalente.
 Un : correspond à la composante non linéaire (grandeur de commande discontinue).
 Lorsque la surface de commutation est atteinte, équation (4.7), on peut écrire :
U  Ueq avec u N  0. (4.16)
La commande Ueq peut être interprétée comme étant la valeur moyenne que prend la commande U
lors des commutations rapides entre ( u Max ) et ( u Min ) :
u
u eq
uMax
t
t
u Min
Fig. IV.8 : La valeur continue u eq prise par la commande lors de la commutation entre u Max et u Min .
UDL – Sidi bel Abbés - 2011 47

61. CHAPITRE : IV Commande par mode glissant de la MSAP
Le vecteur de commande U permet donc de régler les dynamiques des deux modes de
fonctionnement :
 U eq : Permet d'influer sur le mode de glissement. Elle est calculée en sachant que le

comportement du système durant le modèle de glissement est décrit par S ( x )  0 .c’est-a-dire
dans le cas d’un système sans incertitudes. elle est obtenue grâce aux conditions d’invariance de
la surface donnée par l’équation (4.7) : S ( x, t )  0 et 
S ( x, t )  0
 u N
: Permet d'influer sur le mode d'approche, elle est déterminée pour garantir l’attractivité de
la variable à contrôler vers la surface de glissement et satisfaire la condition de convergence, elle
assure l’insensibilité du système aux variations des paramètres [3][4].
IV.8 EXPRESSION ANALYTIQUE DE LA COMMANDE
Nous nous intéressons au calcul de la commande équivalente et par la suite au calcul la commande
attractive du système défini dans l’espace d’état par l’équation (4.8) :

x(t )  f ( x, t )  g ( x, t )u(t )
(4.8)
Le vecteur u est composé par deux grandeurs :
u(t )  ueq (t )  uN (4.15)
On a :
dS S x S  S S

S ( x, t )   .  . x  .  f ( x, t )  g ( x, t )ueq  . g ( x, t )un  (4.17)
dt x t x x x
En mode de glissement, la trajectoire restera sur la surface de commutation S ( x )  0 , autrement dit,

sa dérivée sera nulle S ( x )  0 et u N  0 , l’équation (4.16).
1
 S   S  (4.18)
ueq (t )    f ( x, t )   g ( x, t ) , u N  0
 x   x 
Durant le mode de convergence, en remplaçant le terme u eq par sa valeur (4.18) dans
l’équation(4.17).
(4.19)
S
d’ou : ueq  Lf  Lg
1
Posons : L 
x
Donc, nous obtenons une nouvelle expression de la dérivée de la surface :
(4.20)
S
S ( x )  g ( x, t )uN 

x
UDL – Sidi bel Abbés - 2011 (4.21)48

62. CHAPITRE : IV Commande par mode glissant de la MSAP
Le problème revient à trouver u N tel quel :
S
S ( x ) S ( x )  S ( x ) g ( x, t )u N   0

x
La solution la plus simple est de choisir u N sous la forme de relais, Figure (IV.9). Dans ce cas, la
commande s’écrit comme suit :
uN  K  sign( S ( x))
uN
+K
S ( x)
-K
Fig. IV.9 : définition de la commande
En remplaçant l’expression (4.22) dans (4.21), on obtient :
 S
S ( x)S ( x)  S ( x) K . g ( x, t )  0 (4.23)
x
S
 le facteur g ( x, t ) est toujours négatif pour la classe de système que nous considérons.
x
 Le gain K est choisi positif pour satisfaire la condition (4.23) .Le choix de ce gain est très
influent car s’il est très petit, le temps de réponse sera très grand et s’il est choisi très grand,
nous aurons un temps de réponse très petit et des fortes oscillations au niveau de l’organe de la
commande .Ces oscillations de très haute fréquence, appelées « Chattering » peuvent exciter les
dynamiques négligées ou même détériorer l’organe de commande ou endommager les
actionneurs[11].
IV.9 PHENOMENE DE CHATTERING
Un régime glissant idéal requiert une commande pouvant commuter à une fréquence infinie.
Evidement, pour une utilisation pratique, seule une commutation à une fréquence finie est possible.
Ainsi, durant le régime glissant, les discontinuités appliquées à la commande peuvent entrainer un
phénomène de broutement ou « chattering ». Celui-ci se caractérise par de fortes oscillations des
trajectoires du système autour de la surface de glissement. Le principal raison à l’ origine de ce
phénomène, c’est le caractère discontinu de la commande correspond à la composante discontinue de
la forme « k.sign(S) » qui permet au point de fonctionnement d’osciller autour de la surface de
glissement avec une fréquence élevée sous la forme (4.22) rappelée ci-dessous
u N  K  sign( S ( x))
UDL – Sidi bel Abbés - 2011 49

63. CHAPITRE : IV Commande par mode glissant de la MSAP
C’est pour ça qu’on peut dire que lorsque la surface de commutation est atteinte, condition (4.7), on
peut écrire : u  ueq , u N  0 .
 On a un glissement moins satisfaisant si on a un chattering plus important.
 le phénomène de chattering apparaît clairement dans la courbe de couple électromagnétique,
Cependant le phénomène de chattering sera réduit par des techniques qui sont cité dans le
paragraphe suivant. [3][5][27][28]
IV.10 ELIMINATION DU PHENOMENE DE CHATTERING [7]
Du point de vue de la synthèse de commande, on procède généralement au choix de la surface de
commutation s( x)  0 en fixant le plus souvent la dynamique de glissement, puis on en déduit une
commande discontinue u( x, t )  0 du type, équation (4.2) qui rend cette surface attractive et assure
ainsi l’apparition du mode de glissement.
Ce mode de glissement idéal est illustré par la figure (IV.2). Un mode de glissement idéal correspond
à une commande qui commute à une fréquence infinie or il n’existe aucun organe de commande
pouvant réaliser cette opération. Malgré les différents avantages de la commande par modes de
glissement, son utilisation a été entravée par un inconvénient majeur lié au phénomène de broutement
(phénomène de chattering), figure (IV.10). Ce phénomène est une conséquence naturelle du
comportement dynamique réel de l’ensemble actionneur système à commander.
Le broutement peut provoquer une détérioration anticipée de l’organe de commande ou exciter des
dynamiques hautes fréquences non considérées dans la modélisation du système.
Ainsi, nous allons chercher par différentes méthodes à limiter ce phénomène.
Fig. IV.10 : Mode de glissement avec chattering.
IV.10.1 COMMANDE DISCONTINUE DE BASE
Plusieurs choix pour la commande discontinue un peuvent être faits. Le plus simple consiste à
exprimer la commande discontinue un  [u1, u2.......un] avec la fonction signe par rapport a
s  [s1, s2.......sm]
Sign ( S )  1 si S  0
 (4.24)
Sign ( S )  1 si S  0
UDL – Sidi bel Abbés - 2011 50

64. CHAPITRE : IV Commande par mode glissant de la MSAP
un S’exprime donc :
un  k  sign  ( s( x)) (4.25)
Avec : k Gain positif.
Ce premier choix de la fonction discontinue est représenté sur la figure suivante :
un
K
S (x)
K
Fig. IV.11 : Commande appliquée aux systèmes à structure variable.
IV.10.2 COMMANDE AVEC UN SEUIL
Cette commande est caractérisée par un seuil ε. Dans la bande qui entoure la surface de glissement
s(x ) , seule la composante continue ( ueq ) de la de tension de commande (u = ueq+ un) agit. La partie
discontinue ( un ) étant égale à zéro, les oscillations sur les réponses fortement atténuées. Cependant
lorsque ε augmente, il apparaît un écart statique sur la réponse en régulation. La commande
discontinue est donnée par l’expression :

0 si S ( x)  

un   (4.26)
 Ksign( S ( x )) si S ( x)  


Ce choix de la fonction est représenté par la figure (IV .12) :
ueq 
e(x )
un
+K …...
-ε S(x)
+ε e(x)
….. -K S(x)=0
(b) (a)
Fig. IV.12 : (a) : Traduction de la bande qui entoure la surface dans le plan de phase ;
(b) : Fonction signe avec un seuil.
UDL – Sidi bel Abbés - 2011 51

65. CHAPITRE : IV Commande par mode glissant de la MSAP
Ce type de commande n'est pas très utilisé, car en plus du problème d'erreur statique en présence
d'une perturbation, un intervient avec toute sa valeur et des oscillations peuvent persister en régime
permanent. Un adoucissement de la commande un est donc nécessaire.
IV.10.3 COMMANDE ADOUCIE
Dans le but de diminuer progressivement la valeur de la commande un en fonction de la distance
entre la trajectoire de la variation à régler et la surface de glissement, donc il s’agit d’encadrer la
surface par une bande avec un ou deux seuils. Cette commande est caractérisée par un seuil ( 1) ou
deux seuils (1, 2) pour Diminuer progressivement la valeur de la commande un .
Dans cette configuration présentée par la figure (IV.13), on peut distinguer trois zones dans
l’intervalle positif qui dépendent de la distance du point à la surface de glissement :
 La distance est supérieure au seuil (2) , alors la fonction signe est effective.
 La distance est inférieure au seuil (1), alors un est nul (zone morte)
 Le point dans la bande (1, 2) et alors un est une fonction linéaire de la distance.
K
Droite de pente égale : (4.27)
 2  1
un

e(x)
+K …………….
-ε2 -ε1 S(x)
+ε1 +ε2 P1
P2 e(x)
………….… -K ueq+un
adoucie S(x)=0
un
Fig. IV.13 : Fonction signe de la commande adoucie
Quelle que soit la méthode utilisée, nous remarquons que le seuil est grand, il y a problème de
précision. En effet le système va évoluer dans la bande et risque donc de ne jamais atteindre le point
désirer (origine du plan de phase).
En conclusion, nous pouvons dire que la commande adoucie :
 Limitent voir éliminent les oscillations de glissement.
 de point de vue théorique, le mode de glissement n'existe plus parce que la trajectoire d'état
n'est pas forcée de rester sur s( x )  0 .
UDL – Sidi bel Abbés - 2011 52

66. CHAPITRE : IV Commande par mode glissant de la MSAP
 le système ayant deux points d'équilibre (P1 et P2) et par conséquence, en régime permanent, un
écart statique apparaît et dépend du seuil utilisé.
IV.10.4 COMMANDE CONTINUE AVEC COMPOSANTE INTEGRALE
Les oscillations de haute fréquence qui apparaissent sur les réponses en régime glissant peuvent être
éliminées en convertissant la commande discontinue un , équation (4.26) en commande continue en
remplaçant la fonction signe par la fonction continue voisine :
S ( x)
un  K . (4.28)
S ( x)  
 : est un paramètre définissant le degré d'atténuation des oscillations.
Lorsque   0, on tend vers la même commande discontinue défini par (4.26).
La fonction un est illustrée sur la figure (IV.14) :
un
+K -
S(x)
- -K
Fig. IV.14 : Fonction intégrale de un
Pour augmenter la précision de la réponse du système, on peut utiliser une commande continue
incluant une composante intégrale qui devient active lorsque le point est proche de la surface.
En général, le compensateur intégral diminue l'erreur en régime permanent, mais il est souvent
indésirable pour les régimes transitoires brusques, car il provoque des oscillations supplémentaires sur
la réponse.
La commande un dans ce cas devient :
S( x )
un  K .  (4.29)
S( x )  
Avec :
  0   (4.30)
 0 . S ( x )dt
 
 si S ( x )  
(4.31)
0
 si S ( x )  
UDL – Sidi bel Abbés - 2011 53

67. CHAPITRE : IV Commande par mode glissant de la MSAP
 0 . S ( x )dt

  si S ( x )   (4.32)
0
 si S ( x )  
Où  0 ,  0 , 0 ,  sont des constantes ou paramètres adaptatifs en fonction des références. Ce type
de commande est difficile à mettre en œuvre car il y a un grand nombre de paramètres à déterminer.
IV.10.5 UTILISATION D’UNE SURFACE AUGMENTEE
Le phénomène des oscillations peut être résolu par une méthode différente des méthodes décrites
ci-dessus et qui consiste à augmenter faiblement l’ordre de la surface de glissement. En introduisant la
dérivée de l’erreur dans le calcul de la surface (ce qui revient à introduire un terme d’accélération
dans le cas de l’asservissement de vitesse).
S ( x)  K1e( x)  K2e( x)
 (4.33)
Où : K1 , K2 sont deux constantes positives.
L’emploi d’une surface augmentée entraîne une augmentation de la fréquence de commutation de la
commande d’où une diminution des oscillations.
IV.11 APPLICATION DE LA COMMANDE PAR MODE DE GLISSEMENT A LA MSAP
On rappelle le modèle de la machine synchrone à aimants permanents :
d  R L 1
 dt Id  Id   s Id  q p r Iq  Ud (a )
Ld Ld Ld

d  Rs Ld p f 1
 Iq  Iq   Iq  p r Id  r  Uq (b) (4.34)
 dt Lq Lq Lq Lq
d  p Ld  Lq I d  p f 1 f
 r  r  I q  Cr   r (c)
 dt J J J
IV.11.a Stratégie de réglage à trois surfaces
La figure (IV.15) présent le schéma du réglage par mode glissement utilisant le principe de la
méthode de réglage en cascade, la structure comprend une boucle de régulation de vitesse qui génère
  
la référence de courant Iq laquelle impose la commande Vq .la commande Vd est imposée par la

régulation de courant Id .
UDL – Sidi bel Abbés - 2011 54

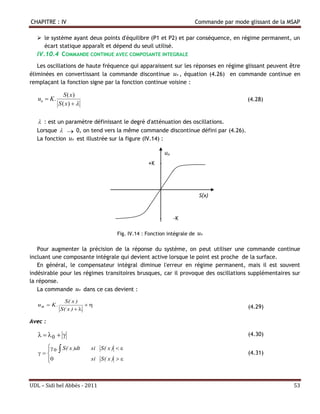
68. CHAPITRE : IV Commande par mode glissant de la MSAP
Fig. IV.15 : schéma global de réglage par mode glissant stratégie de trois surfaces
IV.11.a.1 REGLAGE DE LA VITESSE
La synthèse de commande exploite la technique des modes glissants en utilisant le principe de la
méthode de réglage en cascade, Cette dernière nécessite le choix des surfaces qui assurent les objectifs
de commande. [11][21]
On remarque que d’après l’équation (4.34c), le degré relatif de la vitesse r avec Iq est égal a 1 :
Dans ce cas, l’erreur de réglage est choisie comme la surface :
S (r )   rref  r (4.35)
Par conséquent sa dérivée :
  
S (r )   rref  r (4.36)
La loi de commande est définie par :
Ur  Ureq  Urn (4.37)
Qui est exprimée aussi par la forme suivant :
Iqref  Iqeq  Iqn (4.38)
Si ont remplace l’équation (4.34 c) dans (4.36), on obtient :
  pLd  Lq I d  p f 1 f
S (r )   rref  Iq  Cr   r (4.39)
J J J
Et si on remplace l’équation (4.38) dans (4.39), on obtient :
UDL – Sidi bel Abbés - 2011 55

69. CHAPITRE : IV Commande par mode glissant de la MSAP
  pLd  Lq I d  p f 1 f
S (r )   rref  ( Iqeq  Iqn)  Cr   r (4.40)
J J J
Durant le mode de glissement on a :

S ( r )  0 , S ( r )  0 , Iqn  0 (4.41)
Donc, on déduit la commande équivalente à partir de l’équation (4.40) :

f 1
 rref rref  Cr
I qeq  J J (4.42)
p( Ld  Lq ) 
. Id  p f
J J
Durant le mode de convergence, la dérivée de l’équation de LYAPUNOV doit être négative :
 
V ( r )  S ( r )S ( r )  0 , si en remplace l’équation (4.42) dans (4.40), on obtient :
  pLd  Lq  
S (r )    I d  p f  Iqn (4.43)
 J 
Avec : I qn  kr  sign( S ( r )) (4.44)
k r : Gain positive pour le régulateur de vitesse.
IV.11.a.2 REGLAGE DU COURANT Id
L’expression de courant Id est donnée par l’équation (4.34a):
d  R L 1
I d  I d   s I d  q p r I q  U d (4.34a)
dt Ld Ld Ld
On remarque que d’après l’équation (4.34a),le degré relatif du courant Id avec la commande Ud est
égal à 1:
Donc la variable erreur ed est donnée par :
e d  I dref  I d (4.45)
L’erreur résultante sera corrigée par un régulateur fonctionnant en mode de glissement et la surface
de cette régulation est donnée par :
S ( I d )  I dref  I d (4.46)
Par conséquent la dérivé de la surface :
  
S ( I d )  I dref  I d (4.47)
En tenant compte de l’expression du courant Id déduite dans l’équation du système (4.34a), la
dérivé de cette surface devient :
UDL – Sidi bel Abbés - 2011 56

70. CHAPITRE : IV Commande par mode glissant de la MSAP
  Rs L 1
S ( I d )  I dref  I d  q p  r I q  Ud (4.48)
Ld Ld Ld
Lorsque le régime glissant est atteint, la surface s’annule et par conséquent sa dérivée est donnée
par :
  R L 
S( Id )  0  Udeq   I dref  s I d  q p  r I q  Ld , Udn  0
  (4.49)
 Ld Ld 
D’où
Udref  Udeq  Udn (4.50)
Durant le mode de convergence :

S ( Id ) S ( Id )  0 (4.51)
U dn  Kd sign( S ( I d )) (4.52)
Par conséquent, la commande a la sortie de régulateur dévient:
  R L 
Ud   I dref  s I d  q p  r I q  Ld  Kd sign( S ( I d ))
  (4.53)
 Ld Ld 
K d : Gain positive pour le régulateur de courant direct.
IV.11.a.3 REGLAGE DU COURANT Iq
L’expression de courant Iq est donnée par l’équation (4.34b) :
d  R L p f 1
Iq  Iq   s Iq  d p r Id  r  Uq (4.34b)
dt Lq Lq Lq Lq
La valeur de Iqref a la sortie de régulateur de la vitesse est comparée à celle mesurée. L’erreur
résultante sera corrigée par un régulateur fonctionnant en mode de glissement.
Pour calculer Uqref et Uqn on passe par la même procédure précédente.
La surface de cette régulation est donnée par l’équation suivant:
S ( I d )  I dref  I d (4.54)
Sa dérivée est donnée par :
  
S ( I q )  I qref  I q (4.55)

En remplaçant la valeur Iq de (4.34b) dans l’équation (4.55), on obtient :
   R L p f 1 
S ( I q )  I qref    s I q  d p  r I d  r  Uq  (4.56)
 L Lq Lq Lq 
 q 
UDL – Sidi bel Abbés - 2011 57

71. CHAPITRE : IV Commande par mode glissant de la MSAP
Uqref  Uqeq  Uqn (4.57)

Lorsque le régime glissant est atteint, la surface s’annule: S ( Iq)  0 , S ( Iq )  0 , Donc :
 R L p f 
Uqeq   I qref  s I q  d p  r I d   r  Lq , Uqn  0 (4.58)
 Lq Lq Lq 
 
Pour garantir la convergence on choisi :
U qn  Kq  sign( S ( I q )) (4.59)
En remplaçant la valeur de Uqeq (4.58) et de U qn (4.59) dans Uqref (4.57), on obtient :
 R L p f 
Uqref   I qref  s I q  d p  r I d   r  Lq  K q sign( S ( I q )) (4.60)
 Lq Lq Lq 
 
Avec
K q : Gain positive pour le régulateur de courant quadratique.
IV.11.b RESULTAT DE SIMULATION
Pour la validation de la structure de la commande par mode glissant. On a fait des simulations à
l’aide du logiciel MATLAB/simulink.
Le schéma de simulation est donné par la figure (IV.15).
La figure (IV.16) représente le comportement dynamique de l’ensemble MSAP –onduleur (MLI) avec
régulation par mode glissement, stratégie de trois surfaces.
La simulation est faite comme suit :
Le démarrage à vide pour une consigne de 100 (rad/s) avec application d’un couple résistant Cr=8
(Nm) entre [0.1 et 0.2] (s) puis on inverse le sens de rotation de  r  100 (rad/s) à  r  -100 (rad/s)
à l’instant t = 0.3(s) puis on refait l’application d’un couple résistant Cr =-8 (Nm) entre [0.4 et 0.5] (s).
UDL – Sidi bel Abbés - 2011 58

72. CHAPITRE : IV Commande par mode glissant de la MSAP
ZOOM
-
-
40
8 couple resistante (Nm)
30 Iq(A) 6
20 4
10 Id(A) 2
0 0
-10 -2
-20 -4
-30 -6
-8
-40
0 0.1 0.2 0.3 0.4 0.5 0.6 0 0.1 0.2 0.3 0.4 0.5 0.6
temps(s) temps(s)
40
30 couple éléctromagnetique Ce (Nm)
20
10
0
-10
-20
-30
-40
0 0.1 0.2 0.3 0.4 0.5 0.6
temps(s)
100 40
erreur wr (rad/s) is(A)
50
20
0
-50 0
-100
-20
-150
-40
-200 0 0.1 0.2 0.3 0.4 0.5 0.6
0 0.1 0.2 0.3 0.4 0.5 temps(s)
temps(s)
Fig. IV.16 : réponse de la MSAP avec régulation par mode glissant sans variation paramétrique
IV.11.b.1 TEST DE ROBUSTESSE
Pour mettre en évidence l’importance de la technique de la commande par mode glissant, on va
effectuer des tests de robustesse de notre machine ; et pour vérifier cette dernière :
UDL – Sidi bel Abbés - 2011 59

73. CHAPITRE : IV Commande par mode glissant de la MSAP
1/ on a varié les paramètres électriques de la machine à savoir:
 Rs : La résistance statorique.
2/On fait également varier les paramètres mécaniques à savoir :
 J : Le moment d’inertie.
Les variations introduites dans les essais ressemblent en pratique aux conditions de travail comme
échauffement et le freinage.
a- TEST DE ROBUSTESSE PAR RAPPORT A LA VARIATION DE LA RESISTANCE STATORIQUE
Dans ce test on a triplé et quintuplé la valeur initiale de la résistance statorique. Les résultats
obtenus sont donnés par la figure (IV.17) :
Vitesse de référence
Vitesse réelle (Rs)
Vitesse réelle (3*Rs)
Vitesse réelle (5*Rs)
Fig. IV.17 : comportement dynamique de la MSAP
avec changement de résistance statorique avant le démarrage.
On remarque d’après la figure (IV.17) que la vitesse restera insensible aux variations de la
résistance statorique et cette dernière suit sa consigne avec un temps de réponse très court sans aucun
dépassement.
b- TEST DE ROBUSTESSE PAR RAPPORT A LA VARIATION DE MOMENT D’INERTIE J
150
vitesse de référence Wr(rad/s)
100
Wr( 3*J )
50
0 Wr( 2*J )
Wr( J )
-50
-100
-150
0 0.1 0.2 0.3 0.4 0.5
temps(s)
Fig. IV.18 : comportement dynamique de la MSAP
avec changement de moment d’inertie avant le démarrage.
Pour le moment d’inertie, on a doublé et triplé la valeur initial, on remarque que la vitesse
mécanique suit sa consigne avec un temps de réponse qui est très petit (environ 0.015(s) pour chaque
variation).
UDL – Sidi bel Abbés - 2011 60

74. CHAPITRE : IV Commande par mode glissant de la MSAP
c- INTERPRETATION
Les différentes simulations faites nous permettent de constater que :
 Le rejet de perturbation est très rapide ;
 Un temps de réponse très faible ;
 Une erreur statique pratiquement nulle ;
 Un découplage réalisé avec succès par le maintient de Id nul ;
 Le système répond positivement à ce test, il est insensible aux perturbations internes et
externes, cette commande présente une bonne robustesse.
IV.11.b.2 CONCLUSION
Dans ce chapitre, nous avons présenté la commande à structure variable (CSV) fonctionnant en
mode de glissement appliquée à la machine synchrone à aimants permanents, après la présentation de
la théorie de base de cette commande et le calcul des lois de régulateurs, nous avons réalisé une
simulation de la commande par la méthode de trois surfaces : une structure en cascade ( surface de la
vitesse avec la surface du courant quadratique) et la surface du courant direct.
La commande par mode glissant montre que les performances sont meilleures autour du point de
fonctionnement. Le point fort de cette technique de régulation est la simplicité de mise en œuvre et la
robustesse même en présence des perturbations internes et externes avec un temps de réponse très
faible.
Finalement, on peut conclure que la caractéristique essentielle de cette technique est la capacité de
robustesse dans tout le régime permanent, Néanmoins cette robustesse reste limitée par un
inconvénient du réglage qui réside dans l’existence d’une loi de contrôle discontinu produisant l’effet
de « chattering ».
Le contrôle par mode glissant garanti une bonne insensibilité à la variation paramétrique illustrée
par la poursuite en vitesse est sans dépassement, sans erreur statique, la stabilité et la convergence
vers l’équilibre. On ajoute aussi que la régulation proposée peut être appliquée dans des domaines
exigeants de hautes performances telles que le domaine de la robotique et le domaine des machines
outils.
UDL – Sidi bel Abbés - 2011 61

75. CONCLUSION GENERALE

76. Conclusion générale
CONCLUSION GENERALE
e travail présenté dans ce mémoire est une modeste contribution à l’étude des
performances des commandes appliquées sur la machine synchrone à aimants permanents à
pôles saillant. L'objectif principal de ce mémoire est la réalisation d'une nouvelle commande
robuste par mode glissant qui améliore les performances de la machine.
Afin d'aborder cette étude, on a présenté au premier chapitre, une étude générale sur les aimants
permanents (leurs structures et leurs propriétés), avantages et les domaines d’application qui concerne
la machine synchrone à aimants permanents.
Ensuite, nous avons abordé dans le deuxième chapitre la problématique de la modélisation de la
machine synchrone à aimants permanents en se basant sur les équations électriques et mécaniques
dans le repère (abc) et (d-q).le modèle mathématique de la machine obtenue par la transformation de
PARK en tenant compte des hypothèses simplificatrices qui permettent de réduire la complexité du
système.
L’association convertisseur-machine nous a permis de constater une insuffisance au niveau des
performances. A partir des équations présentées dans le chapitre et les courbes de simulation obtenus
par le logiciel MATLAB/simulink, On a constaté que la machine est non linière et fortement couplé.
Au troisième chapitre, on a donné un aperçu explicite d’une solution parmi les différentes solutions
de découplage, qui est la commande vectorielle. La commande vectorielle permet d’imposer à la
machine synchrone à aimants permanents un comportement semblable à celle de la machine à courant
continu à excitation séparée là ou les courants ne s’affectent pas entre eux.
La commande par mode glissant a fait l’objet d’un quatrième chapitre, c’est une commande robuste
liée aux systèmes à structures variables, dont le but est de palier les inconvénients des commandes
classiques, vu que la Commande a structures variables est par nature une commande non linéaire et
que leur loi de commande se modifie d'une manière discontinue. La robustesse apparait au moment de
l’ajustement automatique des régulateurs à la mise en œuvre (réduction du temps d’ajustement et
amélioration des performances). Le point fort de cette technique de régulation est la simplicité de mise
en œuvre et la robustesse par rapport aux perturbations internes et externes même aux incertitudes du
système. Cependant le principal inconvénient du réglage par mode glissant réside dans l’existence
d’une loi de contrôle discontinu produisant l’effet de chattering. Le choix de la fonction signe adoucie
permet la réduction d’effet de chattering.
Comme perspective, il est intéressant de valider les techniques de notre étude par des essais
expérimentaux, et cherché d’élaborer un modèle mathématique qui assure la stabilité et la poursuite
de consigne même dans le régime transitoire de système.
UDL – Sidi bel Abbés - 2011 62

77. ANNEXE

78. ANNEXE
Paramètres de la machine synchrone à aimants permanents :
Puissance : p = 1.5 KW
La fréquence : F = 50 Hz
Résistance statorique : Rs = 0.6 Ω
Inductance suivant l’axe d : Ld = 1.4 . 10-3 H
Inductance suivant l’axe q : Lq = 2.8 . 10-3 H
Nombre de paire de pôles : P =4
Flux permanent : φ f = 0.12Wb
Moment d’inertie : J = 1.1.10-1 kg.m2
Coefficient de frottement visqueux : f = 1.4.10-3 N.m.s/rad
UDL – Sidi bel Abbés - 2011 63

79. BIBLIOGRAPHIE

80. BIBLIOGRAPHIE
Thèses
[1] M. CARRIERE Sébastien, Synthèse croisée de régulateurs et d'observateurs pour le contrôle robuste
de la machine synchrone, Thèse de doctorat, l'Institut National Polytechnique de Toulouse, France,
année 2010.
[2] HUSSAIN Ayman, Contribution à la commande adaptative robuste par modes glissants, Thèse de
doctorat, Université de Reims Champagne Ardenne, FRANCE, année 2009.
[3] BENMANSOUR Khelifa, Réalisation d’un banc d’essai pour la commande et l’observation des
convertisseurs multicellulaires, Thèse de doctorat, Université de Cergy Pontoise, FRANCE, année 2009.
[4] MASSOUM Ahmed, Contribution à la Commande Singulièrement Perturbée d’une Machine Synchrone
à Aimants Permanents : Commande à Structure Variable (CSV); Commande Neuro-Floue. Thèse de
doctorat, Université de Djilali Liabes , SBA , Algerie, année 2007.
[5] ABID Mohamed , Adaptation de la commande optimisée au contrôle vectoriel de la machine
asynchrone alimentée par onduleur à M.L.I ,Thèse de doctorat, Université de Djilali Liabes ,SBA,
Algerie, année 2006.
[6] FAROOQ Jawad Ahmed, Etude du problème inverse en électromagnétisme en vue de la localisation
des défauts de désaimantation dans les actionneurs à aimants permanents, Thèse de doctorat,
Université de Technologie de Belfort, MONTBELIARD, France. année 2008.
[7] SOSSE ALAOUI Mohammed Chakib, Commande et observateur par modes glissants d’un système de
pompage et d’un bras manipulateur, Thèse de doctorat, université sidi Mohamed ben Abdellah, Fes,
Maroc, année 2009.
[8] CIMUCA Gabriel Octavian, Système inertiel des stockage d’énergie associe a des générateurs
éoliens, Thèse de doctorat, Ecole Nationale Supérieure D’arts et Métiers Centre de Lille, France. année
2005.
[9] GASC Laurent, Conception d’un actionneur à aimants permanents à faibles ondulations de couple
pour assistance de direction automobile Approches par la structure et par la commande, Thèse de
doctorat, Institut National Polytechnique de Toulouse, France, année 2004.
[10] VIDAL Paul-Etienne, Commande non-linéaire d'une machine asynchrone a double alimentation,
Thèse de doctorat, Ecole Nationale Supérieure Electrotechnique, D'électronique, D'informatique,
D'hydraulique et des Télécommunications, TOULOUSE, France, année 2004.
UDL – Sidi bel Abbés - 2011 64

81. Mémoires Magisters
[11] BELABBES Baghdad ,Commande linearisante d’un moteur synchrone à aimants permanents,
mémoire de magister, université djilali liabes, SBA ,Algérie, année 2001
[12] SEKKEL Ahmed Sadreddine, Etude comparative des différentes commandes de la machine à
aimants permanents, mémoire de magister, université djilali liabes SBA, Algérie, année 2008.
[13] REZGUI SALAH EDDINE , Commande de machine electrique en environnement, Matlab/Simulink et
Temps Réel, mémoire de magister, Université Mentouri de Constantine, Algérie, année 2009.
[14] LAHOUEL Dalila,Commande non linéaire adaptative d'une machine synchrone à aimants permanents,
mémoire de magister, Université de Batna, Algérie, année 2009.
[15] BENBRAHIM Amel, Commande prédictive généralisée d’une machine synchrone à aimants
permanents, mémoire de magister, Université de Batna, Algérie, année 2009.
[16] BEN FERDIA Abdelkader, Commande non linéaire d’un moteur synchrone à aimants permanents,
mémoire de magister, Université de Batna, Algérie, année 2006.
[17] BENCHABANE Fateh, Commande en position et en vitesse par mode de glissement d’un moteur
synchrone triphasé à aimants permanents avec minimisation du chattring, mémoire de magister,
Université mohamed khider de Biskra, Algérie, année 2005.
[18] MERZOUG Med Salah, Etude comparative des performances d’un DTC et d’un FOC d’une machine
synchrone à aimants permanents, mémoire de magister, Université de Batna, Algérie.
Mémoire Master
[19] BOUDISSA Ahmed, Synthèse d'observateurs adaptatifs pour la commande sans capteur de la
machine synchrone: application aux véhicules hybride, mémoire de master, Université de Poitiers,
France, Année 2010.
Articles
[20] ADJOUDJ Mohamed, ABID Mohamed, AISSAOUI Abdelghani, RAMDANI Youcef, BOUNOUA Houria,
Commande par mode glissant d’une machine asynchrone à double alimentation montée dans une
éolienne, Revue « Nature et Technologie », janvier 2010.
[21] B.BELABBES, A. MEROUFEL, M.K. FELLAH et M. ABID, Commande à structure par linéarisation
exacte de l’écart d’un moteur synchrone à aimants permanents, Volume 49, Number 2, 2008.
UDL – Sidi bel Abbés - 2011 65

82. [22] KECHICH Abderrahmane et MAZARI Benyounes, La commande par mode glissant : Application à la
machine synchrone à aimants permanents, ISSN 1813-548X, Afrique SCIENCE 04(1), 2008.
[23] A. Kechich1, B. Mazari2 and I. K. Bousserhane, Application of nonlinear sliding-mode control to
permanent magnet synchronous machine, International Journal of Applied Engineering Research , ISSN
0973-4562 Vol.2, No.1 ,2007.
[24] A.BENAISSA et M.K.FELLAH, Commande par mode glissement d’un convertisseur AC/DC avec
correction du facteur de puissance, ACTA ELECTROTEHNICA, volume 47, Number 2,2006.
[25] A.TITAOUINE, F. BENCHABANE, K. YAHIA, PR: A. MOUSSI, Commande d’une machine synchrone à
aimants permanents et estimation de ces paramètres en utilisant le filtre de Kalman étendu, Courrier
du Savoir – N°07, pp.37-43, Décembre 2006.
[26] Abdel Ghani Aissaoui, Hamza Abid, Mohamed Abid, Fuzzy sliding mode control
for a self-controlled synchronous motor drives, Electronic Journal «Technical
Acoustics»,2005
[27] V. I.UTKIN, G. BARTOLINI, A. FERRARA, Adaptive sliding mode control in discrete-time systems,
AUTOMATICA, Vol . 31, No. 5, PP. 769-773, science direct, 1995.
Ouvrages
[28]: Pierre Lopez et Ahmed Saïd Nouri, Théorie élémentaire et pratique de la commande par les
régimes glissants, Mathématiques & Applications, Volume 55, DOI: 10.1007/3-540-34480-2_2,
springerlink, 2006.
[29] Eddie Smigiel et Guy Sturtzer, Modélisation et commande des moteurs triphasés, édition : Ellipses,
Collection : Technosup ,Année 2000.
Encyclopédie
[30] François LEPRINCE-RINGUET, Techniques de l’Ingénieur D2 100, aimants permanents matériaux et
applications.
UDL – Sidi bel Abbés - 2011 66