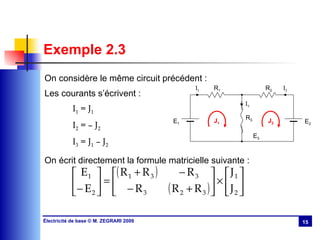
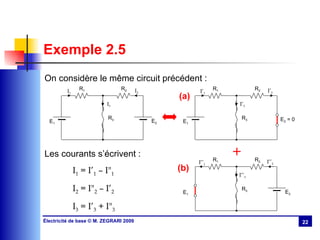
Le chapitre 2 présente les méthodes d'étude des circuits électriques, incluant les lois de Kirchhoff et plusieurs théorèmes tels que ceux de Millman, de superposition, de Thévenin et de Norton. Il aborde également l'analyse des circuits à travers des formulations matricielles et des méthodes de résolution, y compris la détermination des courants dans différentes configurations de circuits. Des exemples illustrent l'application de ces théorèmes et méthodes dans des situations pratiques.

1. Chapitre 2 METHODES D’ É TUDE DES CIRCUITS É LECTRIQUES Prof. Mourad ZEGRARI

2. Plan Notations de base Lois de Kirchhoff Analyse des circuits par les lois de Kirchhoff Théorèmes généraux ( Théorème de Millman, Théorème de superposition, Théorème de Thévenin, Théorème de Norton)

3. Notations de base Réseau Ensemble d’éléments électriques reliés de manière à constituer un circuit fermé. Nœud Point du réseau où se rejoignent au moins trois conducteurs. Branche Groupe d’éléments situé entre deux nœuds successifs. Maille Ensemble de branches reliées dans un circuit fermé (le nœud de départ est le même que celui d’arrivée).

4. Exemple 2.1 On considère le circuit suivant : Nombre de nœuds : n = 2 Nombre de branches : b = 3 Nombre de mailles : m = 3 On distingue : Nombre de nœuds indépendants : N = (n – 1) Nombre de mailles indépendantes : M = b – (n – 1) E 2 E 1 R 1 R 2 R 3 E 3 A B D C F E 1 2

5. Loi de KIRCHHOFF : Nœuds On considère le nœud suivant : La quantité de charge amenée par les courants entrants (+) est égale à celle retirée par les courant sortants (-) : I 1 + I 2 + I 5 = I 3 + I 4 La somme algébrique des courants dans un nœud est nulle : I 1 I 2 I 3 I 4 I 5 A

6. Loi de KIRCHHOFF : Mailles On considère la maille suivante : Si l’on parcoure toute la maille : V AA = V 1 + V 2 + V 3 + V 4 = 0 La somme algébrique des tensions dans une maille est nulle : E 1 R 1 R 2 R 4 D C B A E 2 R 3 E 3 V 1 V 2 V 3 V 4

7. Analyse des circuits électriques L’analyse d’un circuit électrique repose sur la détermination es courants qui circulent dans toutes les branches de ce circuit. Le nombre de branches = b  il faut déterminer ( b ) courants On met en place : N équations de nœuds indépendants M équations de mailles indépendants On dispose de : N + M = b équations.  La détermination de tous les courants devient possible .

8. Formulation des équations Les équations de maille sont reformulées telle que :  E i : Somme algébrique des f.é.m. de chaque maille. Les f.é.m. sont affectées du signe de la borne par laquelle on sort suivant le sens de parcours.  R i I i : Somme des tensions résistives dans chaque maille. Un produit ( R i I i ) est compté positif si le sens du courant I i est le même que celui de parcours de la maille. Il est compté négatif s’il est en sens inverse.

9. Formulation matricielle Les équations de maille sont reformulées sous la forme matricielle suivante : Avec : : Matrice colonne des forces électromotrices. : Matrice (carrée) des résistances. : Matrice colonne des courants.

10. Méthode des déterminants La résolution du système matriciel passe par le calcul des éléments : Déterminant principal : Δ On calcule le déterminant de la matrice des résistances. Déterminants particuliers : Δ Ii Dans la matrice ( R ), on substitue la colonne (i) par la colonne ( E ) des forces électromotrices. Calcul des courants On détermine chaque courant en fonction de son déterminant particulier :

11. Exemple 2.2 On considère le même circuit précédent : Nombre de nœuds : n = 2 Nombre de branches : b = 3 Soit : N = n – 1 = 1 M = b – N = 2 On écrit : Nœud A : I 1 + I 2 = I 3 Maille (1) : E 1 = R 1 I 1 + R 3 I 3 = (R 1 + R 3 ) I 1 + R 3 I 2 Maille (2) : E 2 = R 2 I 2 + R 3 I 3 = R 3 I 1 + (R 2 + R 3 ) I 2 E 2 E 1 R 1 R 2 R 3 E 3 A B 1 2 I 1 I 2 I 3

12. Exemple 2.2 Ce système d’équations peut s’écrire sous la forme matricielle : On obtient alors :

13. Méthode des courants fictifs On associe à chaque maille indépendante un courant fictif J (appelé courant de maille). Tous les courants de maille doivent être choisis dans le même sens. On effectue la formulation matricielle suivante : On calcule les courants J par la méthode des déterminants. On déduit les courants réels par les équations de liaison.

14. Formulation Matricielle La matrice principale est telle que : [E] : Matrice colonne de la somme algébrique des f.é.m. de chaque maille. L’affectation des signes se fait selon le sens de parcours. [R] : Matrice des résistance. Elle est constituée comme suit : R ii > 0 : éléments de la diagonale : Somme des résistances de la maille d’ordre (i). R ij = R ji < 0 : éléments correspondants. Somme des résistances communes aux maille (i) et (j) avec le signe négatif. [J] : Matrice colonne des courants fictifs de caque maille.

15. Exemple 2.3 On considère le même circuit précédent : Les courants s’écrivent : I 1 = J 1 I 2 = – J 2 I 3 = J 1 – J 2 On écrit directement la formule matricielle suivante : E 2 E 1 R 1 R 2 R 3 E 3 J 1 J 2 I 1 I 2 I 3

16. Exemple 2.3 On obtient : Soit :

17. Diviseur de tension Une source de tension (E, R 1 ) alimente une résistance R 2 : La loi des mailles donne : E = V 1 + V 2 = (R 1 +R 2 ) I La tension V 2 aux bornes de la résistance R 2 s’écrit : E R 1 R 2 I V 2 V 1 Équation d’un diviseur de tension.

18. Diviseur de courant Une source de courant ( I 0 , R 1 ) alimente une résistance R 2 : La loi des nœuds donne : Le courant I 2 qui circule dans la résistance R 2 s’écrit : Équation d’un diviseur de courant. R 1 R 2 I 0 V I 0 I 2 I 1

19. Théorème de Millman On considère le nœud suivant : La loi des nœuds au point M donne : Soit : Théorème de Millman. I 1 I 2 I 3 I 4 A 1 R 1 A 2 R 2 R 3 A 3 R 4 A 4 M

20. Exemple 2.4 On désire calculer le potentiel au point A : Le théorème de Millman donne directement : 100  V 500  200  6 V 10 V 8 V A B

21. Théorème de Superposition On considère un système linéaire possédant une sortie S et plusieurs entrées Ei : La sortie S du système soumis simultanément à plusieurs entrées E i est égale à la somme des réponses S i du système à chaque entrée E i appliquée séparément : Système Linéaire E 1 E 2 E n S E 1 active et E i(i≠1) = 0  S = S 1 E 2 active et E i(i≠2) = 0  S = S 2 E n active et E i(i≠n) = 0  S = S n

22. Exemple 2.5 On considère le même circuit précédent : Les courants s’écrivent : I 1 = I’ 1 – I &quot; 1 I 2 = I &quot; 2 – I’ 2 I 3 = I’ 3 + I &quot; 3 E 2 = 0 E 1 R 1 R 2 R 3 I’ 1 I’ 2 I’ 3 E 2 E 1 R 1 R 2 R 3 I’’ 1 I’’ 2 I’’ 3 (a) (b) E 2 E 1 R 1 R 2 R 3 I 1 I 2 I 3

23. Exemple 2.5 On calcule les différents courants : E 2 E 1 = 0 R 1 R 2 R 3 I’’ 1 I’’ 2 I’’ 3 E 2 = 0 E 1 R 1 R 2 R 3 I’ 1 I’ 2 I’ 3 R eq1 (b) : (a) : R eq2

24. Théorème de Thévenin Tout réseau actif vu entre deux points A et B, peut être modélisé par un générateur de tension, de force électromotrice E T et de résistance interne R T : Réseau Actif B A E T R T A B E T : Différence de potentiel à vide entre les points A et B. E T = (V A – V B ) I =0 R T : Résistance équivalente du réseau passif vu entre A et B. On court-circuite les sources de tension et on ouvre les sources de courant

25. Exemple 2.6 On désire calculer le courant I dans la résistance R : Les courant I est donné par la relation : E R 1 A R 2 I B R C E T R T A I B R C

26. Exemple 2.6 Déterminons les paramètres E T et R T : On obtient : et E R 1 A R 2 B E T E T : R 1 A R 2 B R T : R eq

27. Théorème de Norton Tout réseau actif vu entre deux points A et B, peut être modélisé par un générateur de courant, de courant électromoteur I N et de résistance interne R N : Réseau Actif B A I N : Courant de court-circuit quand les points A et B sont reliés. I N = I CC (VAB=0) R N : Résistance équivalente du réseau passif vu entre A et B. R N = R eq(AB) I N R N A B

28. Exemple 2.7 On désire calculer le courant I dans la résistance R : Les courant I est donné par la relation : I N R N A I B R C E R 1 A R 2 I B R C

29. Exemple 2.7 Déterminons les paramètres I N et R N : On obtient : et E R 1 A R 2 B I N I N : R 1 A R 2 B R N : R eq

30. Equivalence Thévenin-Norton Un même réseau actif peut être modélisé soit par un générateur de tension (Thévenin) ou de courant (Norton). Comme ces générateurs représentent le même réseau, on peut alors établir l’équivalence suivante : Soit : et E T R T A B I N R N A B