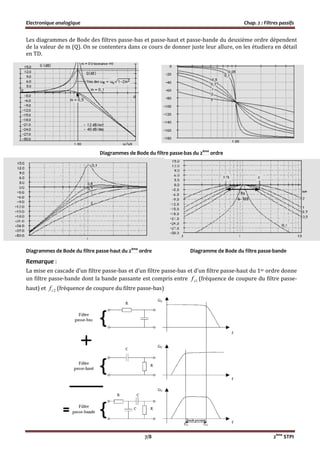
Le chapitre 2 sur les filtres passifs présente les concepts fondamentaux des filtres, y compris leurs définitions, fonctions de transfert, fréquences de coupure, et les décibels en électricité. Il discute également des différents types de filtres (passe-bas, passe-haut, passe-bande, et coupe-bande) ainsi que les filtres du 1er ordre et leurs applications. Les diagrammes de Bode sont utilisés pour visualiser les caractéristiques des filtres en représentant le gain et la phase en fonction de la fréquence.

1. Electronique analogique Chap. 2 : Filtres passifs
1 /8 2ème
STPI
Chapitre 2 :
Filtres passiFs
I. Généralités sur le filtrage :
1.1. Définitions :
Le filtre est un quadripôle linéaire qui ne laisse passer que certaines composantes fréquentielles du signal
appliqué à l’entrée et bloquerais d’autres fréquences.
Le domaine de fréquences est l’intervalle ou la bande de fréquences ou le signal est tranmis.
Un filtre passif est un filtre constitué avec des éléments passifs linéaires R, L, C.
Un filtre actif contient des éléments actifs (amplificateur, transistors..) et des composants passifs, ils
nécessitent une alimentation pour les éléments actifs.
1.2. Fonction de transfert d’un filtre :
On définit la fonction de transfert complexe d’un quadripôle le gain en tension dans le domaine
harmonique :
)(
)(
)(
)(
)( 



 jj
e
S
ejH
jV
jV
jH 
avec :
e
S
V
V
jH )(  : est le gain du filtre
)()(  eS  : est la phase de la fonction de transfert.
1.3. Fréquence de coupure :
La fréquence de coupure d’un filtre est définie comme étant la fréquence pour laquelle le module de la
fonction de transfert le module de la fonction de transfert (le gain) vaut sa valeur efficace.
2
)(
)( max


jH
jH c 
1.4. Le Décibel :
 Décibel sonore :
Au son le plus faible perceptible par l’oreille humaine, on fait correspondre la valeur 0 Bel (la puissance
correspondante est notée : WPref
12
10
 .
- Une puissance de (P = 10. refP ) correspond à 1 Bel soit 10 décibel (dB).
- Une puissance de (P= 100. refP ) correspond à 2 Bel soit 20 (dB).
- Une puissance de (P = ref
n
P.10 ) correspond à n Bel soit (10.n) dB
)(log.10 10 PPdB 
 Décibel en électricité :
On définir, comme pour le son, le gain en puissance d’un quadripôle en général, la quantité pG , donnée
par l’expression :  eSp PPG log.10 en dB. SP et eP sont, respectivement, les puissances disponibles
en sortie et en entrée.
pG est exprimé en dB, soit  eSV VVG log20 en dB ( SV la tension de sortie et eV la tension de
l’entrée)
Remarque : La valeur du gain en tension d’un quadripôle qui correspond à sa valeur efficace est égale à
la valeur maximale moins 3dB. La fréquence de coupure, c , est donc la fréquence qui donne une
atténuation de 3dB du gain maximum (pris en dB) : dBGG VcV 3)( max  ,

2. Electronique analogique Chap. 2 : Filtres passifs
2/8 2ème
STPI
1.5. Diagrammes de Bode :
Une fonction de transfert, étant complexe, sa représentation comprend deux graphes l’un pour le module et
l’autre pour la phase en f onction de la pulsation (la fréquence).
L’échelle des phénomènes rencontrés étant très grande, la représentation habituellement utilisée est
logarithmique. Le plan de Bode est donc l’ensemble de deux courbes suivantes :
– La courbe du gain :  )log()( fdBGV  .
– La courbe du gain :  )log()(  f
 Echelle linéaire :
 Echelle logarithmique :

0
1
0
1
logloglog
x
x
x
x
rx
si r = 2 → c’est une octave
si r = 10 → c’est une décade.
Les diagrammes de Bode peuvent se présenter sous forme de courbes réelles ou de courbes asymptotiques.
 Courbes réelles : C’est l’étude graphique de la fonction G(dB) en fonction de la pulsation.
 Courbes asymptotiques : c’est la représentation graphique simplifiée à l’aide de leurs équivalents
aux bornes du domaine de définition ( cet   ,0 ).
Propriété importante :
Lorsque la fonction du transfert )( jH d’un filtre peut se décomposer sous la forme d’un produit de deux
fonctions de transfert élémentaire )(1 jH et )(2 jH alors le diagrammes de Bode peuvent se tracer en
additionnant les diagrammes de Bode de )(1 jH et )(2 jH
)().()( 21  jHjHjH      )().(log20)(log20 21  jHjHjH 
   )(log20)(log20 21  jHjH 
        )(arg)(arg)().(arg)(arg 2121  jHjHjHjHjH 
II. Etudes des filtres du 1er
ordre :
2.1. Différents types des filtres :
Les filtres peuvent être classés soit par :
1. Leur fonction, ainsi on distingue :
 Filtre passe-bas : ne laisse passer que les composantes fréquentielles inférieures ou égale à la
fréquence de coupure et atténue les fréquences supérieures (figure a)
 Filtre passe-haut : ne laisse passer que les composantes fréquentielles supérieures ou égale à
la fréquence de coupure et atténue les fréquences inférieures (figure b)
 Filtre passe-bande : ne laisse passer que les composantes appartenant à la bande de
fréquences comprise entre la fréquence de coupure basse et la fréquence de coupure haute du
filtre (figure c)
 Filtre coupe-bande : atténue les composantes fréquentielles appartenant à la bande de
fréquences comprises entre la fréquence de coupure basse et la fréquence de coupure haute
(figure d).
x1 x2 x3 x4 x5
unité x = x 1-x0 = x2-x1 = ....=cste
Echelle x = unité de longueur
x0
x
log(x 1
)
log(x 2)
log(x 3)
log(x 4)
log(x 5
)
unité x = logx 1
-log(x 0
) = log(x 2
)-log(x 1
) = ....=cste
log(x 0)
log(x)

3. Electronique analogique Chap. 2 : Filtres passifs
3/8 2ème
STPI
2. leur ordre : l’ordre d’un filtre est le degrés le plus élevé du polynôme en  qui apparaît dans le
dénominateur de la fonction de transfert.
Exemple :
Filtre du 1er ordre :
DC
BA
jH





)(1
CB
A
jH



)(2
Filtre du 2ème ordre :
22
2
2
11
2
1
1 )(
CBA
CBA
jH






22
2
2
1
2
1
2 )(
CBA
BA
jH






22
2
2
1
3 )(
CBA
A
jH




2.2.Intégrateurs :
La fonction de transfert d’un intégrateur est de la forme :
0
1
)(


j
jH 
 0)( jH 
 





90)(
log20)(log20)( 0

 HGdB
- Pour 0   dBG 0)( 0 
- Pour 0   )(G
- Pour 0   )(G
Le gain )(G décroît en fonction de la pulsation avec une pente de -20dB/dec.
2.3.Dérivateur :
La fonction de transfert d’un intégrateur est de la forme : 0)(  jjH 
0)(  jH 





90)(
log20)(log20)( 0

 HGdB
- Pour 0   dBG 0)( 0 
- Pour 0   )(G
- Pour 0   )(G
Gv
(dB)
fc f
Figure - a-
Gv
(dB)
fc f
Figure - b-
Gv
(dB)
fc1 f
Figure - c-
fc2
fc1
fc2 f
Gv
(dB)
Figure - d-
bande
transmise
bande
transmise
bande
transmise
bande
transmise
bande
coupée
bande
coupée
bande
coupée
bande
coupée

4. Electronique analogique Chap. 2 : Filtres passifs
4/8 2ème
STPI
Le gain )(G décroît en fonction de la pulsation avec une pente de +20dB/dec.
2.4.Filtre passe-bas du 1er
ordre :
La fonction de transfert d’un filtre passe-bas du 1ère ordre est de la forme :
01
1
)(


j
jH


 2
01
1
)(



jH 
    
 





0
2
0
2
0
arctan)(
1log101log20)(log20)(

 HGdB
Etude du gain :
Cherchons les asymptotes
- Pour 0   dBG 3)( 0  : 0 est le fréquence de coupure à -3dB ;  45)( 0
- Pour 0   0)( G : asymptote parallèle à l’axe des abscisses.
- Pour 0   )(G :  0)( jjH  et 0log20log20)(  G :
Asymptote oblique de pente -20dB/dec.
L’intersection des deux asymptotes est le point 0 
La représentation asymptotique est donc composée de deux asymptotes :
 Une asymptote parallèle à l’axe des abscisses pour 0  .
 Une asymptote oblique de pente -6dB/octave ou -20dB/dec pour 0 
Etude de l’argument:
Cherchons les asymptotes
- Pour 0    45)( 0
- Pour 0    0)( : asymptote parallèle à l’axe des abscisses.
- Pour 0    90)( : asymptote parallèle à l’axe des abscisses
La représentation asymptotique est donc composée de deux asymptotes :
 Une asymptote parallèle à l’axe des abscisses pour 0  (  0 )
 Une asymptote parallèle à l’axe des abscisses pour 0  (  90 )
Les applications sont nombreuses. On peut citer son rôle de moyenneur, c'est-à-dire récupérer la
valeur moyenne d’un signal périodique (la fréquence f =0 Hz).
Dans les hauts parleurs, il permet de sélectionner les graves (basses fréquences).

5. Electronique analogique Chap. 2 : Filtres passifs
5/8 2ème
STPI
Exemples de filtres passe-bas :
 Circuit R-C :


jRC
jH


1
1
)( , la fréquence de coupure est :
RC
1
0 
 Circuit L-R


R
L
j
jH


1
1
)( , la fréquence de coupure est :
R
L
0
Le comportement de deux cellules R-C et L-R est identique, mais le filtre passe-bas L-R est moins
répondu du fait des inconvénients de la bobine :
- Rayonnement électromagnétique.
- Encombrement et masse,
- Prix élevé
2.5.Filtre passe-haut du 1er
ordre :
La fonction de transfert d’un intégrateur est de la forme :
0
0
1
)(



j
j
jH


 
 2
0
0
1
)(




jH 
    
 




0
2
00
arctan90)(
1log10log20)(log20)(

 HGdB
Etude du gain :
Cherchons les asymptotes
- Pour 0   dBG 3)( 0  : 0 est le fréquence de coupure à -3dB ;  45)( 0
- Pour 0    0log20)(  G : Asymptote oblique de pente +20dB/dec.
- Pour 0   0)( G Une asymptote parallèle à l’axe des abscisses.
L’intersection des deux asymptotes est le point 0 
La représentation asymptotique est donc composée de deux asymptotes :
 Une asymptote parallèle à l’axe des abscisses pour 0  .
 Une asymptote oblique de pente 6dB/octave ou +20dB/dec pour 0 
Etude de l’argument:
Cherchons les asymptotes
- Pour 0    45)( 0
- Pour 0    0)( : asymptote parallèle à l’axe des abscisses.
- Pour 0    90)( : asymptote parallèle à l’axe des abscisses
La représentation asymptotique est donc composée de deux asymptotes :
 Une asymptote parallèle à l’axe des abscisses pour 0  (  0 )
 Une asymptote parallèle à l’axe des abscisses pour 0  (  90 )

6. Electronique analogique Chap. 2 : Filtres passifs
6/8 2ème
STPI
Contrairement au filtre passe-bas, le filtre passe-haut permet de supprimer la composante continue d’un
signal, comme par exemple la position AC à l’entrée des oscilloscopes. Il faut dans ce cas une fréquence de
coupure inférieure à1Hz.
Dans les hauts parleurs, il permet de sélectionner les aiguës (hautes fréquences).
Exemples de filtres passe-haut :
 Circuit C-R :



jRC
jRC
jH


1
)( , la fréquence de coupure est :
RC
1
0 
 CircuitR-L



R
L
j
R
L
j
jH


1
)( , la fréquence de coupure est :
R
L
c 
III. Filtres du second ordre :
Pour les filtres du second ordre, le dominateur de la fonction de transfert est un polynôme d’ordre 2 en  .
3.1.Filtre passe-bas du 2nd
ordre :
La fonction de transfert d’un filtres passe-bas du second ordre s’écrit sous la forme suivant :
   2
0021
1
)(




jm
jH , m : le facteur d’amortissement du filtre.
)( jH peut être exprimée en fonction du facteur qualité
m
Q
2
1
 →
   2
001
1
)(




Qj
jH
3.2.Filtre passe-haut du 2nd
ordre :
La fonction de transfert d’un filtre passe-haut du second ordre s’écrit sous la forme suivant :
 
   2
00
2
0
21
)(






jm
jH , m : le facteur d’amortissement du filtre.
)( jH peut être exprimée en fonction du facteur qualité :
m
Q
2
1
 →
 
   2
00
2
0
1
)(






Qj
jH
3.3.Filtre passe-bande :
La fonction de transfert d’un filtre passe-bande s’écrit sous la forme suivant :
 
   2
00
0
21
2
)(





jm
jm
jH , m : le facteur d’amortissement du filtre.
)( jH peut être exprimée en fonction du facteur qualité
m
Q
2
1
 →
 
   2
00
0
1
)(





Qj
Qj
jH

7. Electronique analogique Chap. 2 : Filtres passifs
7/8 2ème
STPI
Les diagrammes de Bode des filtres passe-bas et passe-haut et passe-bande du deuxième ordre dépendent
de la valeur de m (Q). On se contentera dans ce cours de donner juste leur allure, on les étudiera en détail
en TD.
Diagrammes de Bode du filtre passe-bas du 2ème
ordre
Diagrammes de Bode du filtre passe-haut du 2ème
ordre Diagramme de Bode du filtre passe-bande
Remarque :
La mise en cascade d’un filtre passe-bas et d’un filtre passe-bas et d’un filtre passe-haut du 1er ordre donne
un filtre passe-bande dont la bande passante est compris entre 1cf (fréquence de coupure du filtre passe-
haut) et 2cf (fréquence de coupure du filtre passe-bas)

8. Electronique analogique Chap. 2 : Filtres passifs
8/8 2ème
STPI
IV. Fonction de transfert quelconque :
D’une manière générale, la fonction de transfert peut s’écrire comme suit :
0
1
1
0
1
1
)(
bpbpb
apapa
jH l
l
l
l
k
k
k
k


 





 , avec kl  et jp 
Cette fraction rationnelle comprend un polynôme en p d’ordre k en numérateur et un polynôme d’ordre l
au dénominateur. Sauf exception le degrés du dominateur est tjrs inférieur ou égal à celui du dominateur
La fonction de transfert à étudier peut donc se mettre sous la forme :
ordreduetdufonctionsdeproduit
ordreduetdufonctionsdeproduit
jH nder
nder
21
21
)( 
Ainsi, il sera toujours possible de réaliser les filtres analogiques d’ordre supérieur en cascadant des filtres
du 2ème ordre (si l’ordre est pair) et des filtres du 2ème ordre et un filtre du 1er ordre (si l’ordre est impair)
Exemple :
   )().().(
211
)( 3212
0
2
00
0



 jHjHjH
jmj
j
jH 

 ,
avec 01 )(  jjH 
0
1
1
1
)(


j
jH

 2
0
2
0
3
21
1
)(




mj
jH
Les diagrammes de Bode sont :





)()()()(
)()()()(
321
321

 dBdBdBdB GGGG
Filtre d'ordre
N
Filtre
d'ordre 2
Filtre
d'ordre 2
Filtre
d'ordre 2
Filtre
d'ordre 2
Filtre
d'ordre 1
  
Décomposition d'un filtre d'ordre N (pair) à m filtres élementaires d'ordre 2
  
Décomposition d'un filtre d'ordre N (impair) à m filtres élementaires d'ordre 2 + un filtre d'ordre 1