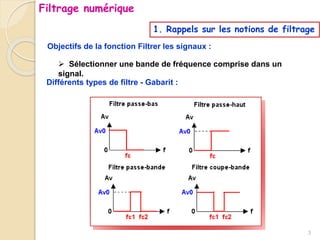
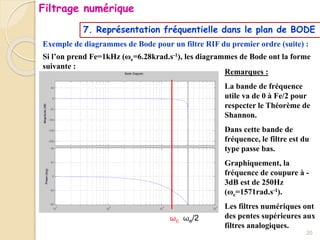
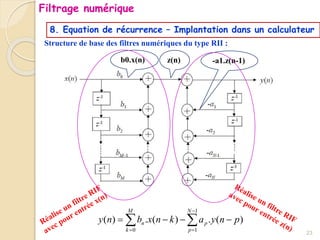
Le document traite du filtrage numérique, en abordant les concepts de base, les types de filtres et les équations différentielles associées. Il présente également les avantages et inconvénients des filtres numériques, leurs principes de fonctionnement, ainsi que des méthodes de synthèse. Enfin, il explique la stabilité des filtres numériques et inclut des exemples d'équations de récurrence.

1. BTS 2ème SE - 2012/2013
Lycée ALKHAWARIZMI-
Casa
Physique appliquée
1

2. Plan de la présentation
1. Rappels sur les notions de filtrage
a. Objectifs de la fonction Filtrer les signaux
b. Types de filtre – Gabarits
c. Expression des filtres par les équations différentielles
2. Avantages et inconvénients du filtrage numérique
3. Principe des filtres numériques
4. Filtres RII et RIF
5. Stabilité des filtres
6. Synthèse des filtres
a. Par approximation des différentielles par des différences finies
b. Par la transformée bilinéaire
7. Réponse fréquentielle dans le plan de Bode
8. Implantation dans un calculateur – Equation de récurrence
2
Filtrage numérique

3. 1. Rappels sur les notions de filtrage
Objectifs de la fonction Filtrer les signaux :
 Sélectionner une bande de fréquence comprise dans un
signal.
Différents types de filtre - Gabarit :
3
Filtrage numérique

4. 1. Rappels sur les notions de filtrage
Equation différentielle d’un filtre analogique :
Les équations différentielles sont une autre méthode permettant de
caractériser un filtre.
Prenons 2 exemples avec des filtres passifs du 1er et du 2nd ordre :
Exemple 1 : Filtre du 1er ordre
La loi des mailles nous donne :
1( ) ( ) 2( ) 0
R
u t u t u t
  
Or : ( ) . ( )
2( )
( ) .
R C
C
u t R i t
du t
i t C
dt







On obtient donc :
2( )
. 2( ) 1( )
du t
RC u t u t
dt
 
4
Filtrage numérique

5. Exemple 2 : Filtre du 2nd ordre
La loi des mailles nous donne :
1( ) ( ) ( ) 2( ) 0
R L
u t u t u t u t
   
Or : ( ) . ( )
2( )
( ) .
( )
( ) .
R
L
u t R i t
du t
i t C
dt
di t
u t L
dt

 









On obtient donc :
2
2
2( ) 2( )
. . 2( ) 1( )
d u t du t
LC RC u t u t
dt dt
  
Qui est une équation différentielle du second ordre à coefficient
constant.
Grâce à la Transformée de Laplace, on
obtient :
 
   
2
2
2
2
2
2( ) 2( )
. . 2( ) 1( )
2( ) 2( )
. . 2( ) 1( )
. . 2( ) . . 2( ) 2( ) 1( )
d u t du t
TL LC RC u t TL u t
dt dt
d u t du t
LC TL RC TL TL u t TL u t
dt dt
LC p U p RC pU p U p U p
 
  
 
 
   
   
   
 
 
     
2
2
2( ) 1
1( ) 1
2( ) 1
1( ) 1
U p
U p RCp LCp
U j
U j RCj LC j

  


  

 
 
  

Qui est bien la fonction de transfert d’un filtre du second ordre.
Filtrage numérique
5
1. Rappels sur les notions de filtrage

6. 2. Avantages/Inconvénients du filtrage numérique
Avantages des filtres numériques / analogiques :
 Pas d’utilisation de composants discrets tels que R, C et L;
Pas de modification par conséquent des caractéristiques du filtre;
Possibilité d’obtenir des filtres d’ordre très élevé sans difficulté (100 à 200),
donc des atténuations très importantes.
Inconvénients des filtres numériques / analogiques :
 Echantillonnage du signal d’entrée analogique => Choix de la fréquence
d’échantillonnage Fe (dans tous les cas, il faut respecter le théorème de
Shannon Fe>2.Fmax);
 Calcul parfois complexe pour obtenir la fonction de transfert du filtre
numérique;
 Nécessite un calculateur puissant (caractérisé par son MIPS ou GIPS =
nombre d’Instructions Par Seconde);
 S’assurer de la stabilité du filtre numérique en fonction de la quantification
des coefficients et de la fréquence d’échantillonnage.
Filtrage numérique
6

7. 3. Principe des filtres numériques
FILTRE NUMERIQUE
Le filtre numérique transforme la suite d’échantillon d’entrée x(nTe) en une
suite d’échantillon y(nTe).
Filtre
numérique
xnTe
ynTe
Bien souvent, on oublie volontairement le terme Te qui représente la période
d’échantillonnage.
( 2)
( ) ( ) (( 2). ) ( 2)
nTe n Te
x x nTe x n et x x n Te x n

     
Notation :
Filtrage numérique
7

8. 4. Filtre RII et Filtre RIF
Les filtres numériques possèdent aussi leurs représentations :
 Relation de récurrence;
 Fonction de transfert en z appelé aussi transmittance.
Représentation du filtre numérique par sa relation de récurrence :
0 0
. ( ) . ( )
N M
k j
k j
a y n k b x n j
 
  
 
Où :
 les ak et bj des coefficients dépendant du type de filtre numérique réalisé;
 x(n-j) représente l’échantillon de l’entrée, j coups d’horloge précédent;
 y(n-k) représente l’échantillon de la sortie, k coups d’horloge précédent.
On distingue 2 types de filtre numérique :
Si N=0 : on parle de filtre à Réponse Impulsionnelle Finie (RIF ou FIR en
anglais).
Si N≥1 : on parle de filtre à Réponse Impulsionnelle Infinie (RII ou IIR en
anglais).
En analogique : Equation différentielle, et Fonction de Transfert en jω (ou p).
: 2. ( ) 0,2. ( 1) 1,5. ( ) 0,48. ( 1) 0,12. ( 2)
Exemple y n y n x n x n x n
      
Filtrage numérique
8

9. Représentation du filtre numérique par sa relation de récurrence (suite) :
( ) ( ) 0,2. ( ) 1,5. ( 1) 0,48. ( 2) 0,12. ( 3)
y n y nTe x n x n x n x n
       
Exemple de filtre numérique RIF :
( ) 1,3. ( ) 0,26. ( 1) 0,08. ( 1) 0,79. ( 2)
y n x n x n y n y n
      
Exemple de filtre numérique RII :
Représentation du filtre numérique par sa Fonction de Transfert en z :
A l’image de la Transformée de Laplace en analogique de variable p, il existe
aussi une transformée en numérique appelé Transformée en Z de variable z.
La transformée en Z n’étant pas au programme, on donnera la Fonction de
Transfert en z à partir de la relation de récurrence.
La Fonction de Transfert d’un filtre numérique peut donc s’écrire par :
( )
( )
( )
Y p
H p
X p

En analogique
( )
( )
( )
Y z
H z
X z

En numérique
Filtrage numérique
9
4. Filtre RII et Filtre RIF

10. ( ) 1,3. ( ) 0,26. ( 1) 0,08. ( 1) 0,79. ( 2)
y n x n x n y n y n
      
Exemple de Fonction de Transfert en z d’un filtre numérique RII :
Représentation du filtre numérique par sa Fonction de Transfert en z (suite) :
1
1 2
( ) 1,3 0,26.
( )
( ) 1 0,08. 0,79.
Y z z
H z
X z z z

 

 
 
Méthode :
 On transforme les u(n-k) par z-k.U(z);
 On regroupe tous les termes en X(z) ensemble et les termes en Y(z) ensemble;
 On établit ensuite la fonction de transfert H(z)=Y(z)/X(z).
Pour notre exemple, cela donne :
1 1 2
( ) 1,3. ( ) 0,26. . ( ) 0,08. . ( ) 0,79. . ( )
Y z X z z X z z Y z z Y z
  
   
   
1 2 1
( ). 1 0,08. 0,79. ( ). 1,3. 0,26.
Y z z z X z z
  
   
La Fonction de Transfert en z est donc :
Ou encore en fonction des puissances positives de z :
 
2
. 0,26 1,3.
( )
( )
( ) 0,79 0,08.
z z
Y z
H z
X z z z

 
 
L’opérateur z-1 représente un retard d’un échantillon.
Filtrage numérique
10
4. Filtre RII et Filtre RIF

11. 5. Stabilité des filtres numériques
Théorème de stabilité :
Un filtre numérique est stable si tous les pôles de la Fonction de Transfert en
z sont à l’intérieur du cercle unité.
Pour étudier la stabilité d’un filtre numérique de Fonction de Transfert
H(z), il faut déterminer l’ensemble des pôles de celle-ci.
     
1 2
( ) . n
Den z z z z z z z
   
Par conséquent, il faut rechercher les racines du dénominateur pour l’écrire
sous la forme :
Et vérifier que tous les pôles zi sont bien dans le cercle unité (module < 1).
Remarque : Pour vérifier que tous les pôles sont dans le cercle unité on peut
calculer le module des zi.
11
Filtrage numérique

12. Exemple de vérification de la stabilité d’un filtre RII :
Reprenons l’exemple précédent où la transmittance est :
 
2
. 0,26 1,3.
( )
( )
( ) 0,79 0,08.
z z
Y z
H z
X z z z

 
 
Cherchons les racines du dénominateur :
2
1 2
( ) 0,08. 0,79 ( 0,04 0,888 ) . ( 0,04 0,888 )
Den z z z z j z j
z z
   
   
         
   
   
   
Vérifions que ces 2 pôles sont dans le cercle unité :
 
 
1
2
0,04 0,888 0,889 92,58
0,04 0,888 0,889 92,58
z j
z j
     


   


Les modules des 2 pôles sont bien inférieurs à 1, donc les pôles sont dans
le cercle unité.
Le filtre étudié est donc stable.
12
Filtrage numérique
5. Stabilité des filtres numériques

13. 6. Synthèse des filtres numériques
L’objectif de la synthèse des filtres numériques est de trouver l’équation de
récurrence ou la Fonction de Transfert en z (Transmittance en z) d’un filtre
pour respecter un cahier des charges (gabarit du filtre).
2 méthodes de synthèse sont au programme :
 Par discrétisation de l’équation différentielle;
 Par la transformation bilinéaire.
0 0
. ( ) . ( )
( )
( )
( )
N M
k j
k j
a y n k b x n j
ou
Y z
H z
X z
 
  

 
13
Filtrage numérique

14. Approche par discrétisation de l’équation différentielle :
6. Synthèse des filtres numériques
Objectif : A partir d’une équation différentielle (ou d’une Fonction de Transfert
d’un filtre analogique), obtenir l’équation de récurrence ou la transmittance en
z du filtre numérique qui se rapproche du filtre analogique équivalent.
On se limitera aux filtres analogiques du second ordre qui ont donc une
équation différentielle du second ordre.
Méthode de la discrétisation de l’équation temporelle :
 Si on dispose de la fonction de Transfert en analogique H(p) ou H(jω),
revenir à l’équation différentielle par la Transformée de Laplace Inverse;
 Remplacer :
 les fonctions par :
 les dérivées premières par :
 les dérivées secondes par :
 Si on souhaite obtenir la transmittance, reprendre la méthode
permettant de passer de l’équation de récurrence à la transmittance vue
précédemment.
( ) ( ) ( 1)
dx t x n x n
dt Te
 

2
2 2
( ) ( ) 2. ( 1) ( 2)
d x t x n x n x n
dt Te
   

( ) ( )
x t x n

14
Filtrage numérique

15. Approche par discrétisation de l’équation différentielle (suite) :
6. Synthèse des filtres numériques
Exemple pour un filtre du 1er ordre du type passe bas :
Soit un filtre analogique ayant pour équation différentielle : ( )
. ( ) ( )
dy t
a y t x t
dt
 
En discrétisant l’équation différentielle, il vient :
( ) ( ) ( 1)
. ( ) ( ) . ( ) ( )
dy t y n y n
a y t x t a y n x n
dt Te
 
    
L’équation de récurrence s’écrit donc :
1
( ) . ( ) . ( 1) . ( ) . ( 1)
1 . 1 .
A B
Te
y n x n y n A x n B y n
aTe aTe
   
     
   
 
   
La Fonction de Transfert en z (ou transmittance en z) s’écrit donc :
1
( ) .
( ) 1 .
Y z A A z
X z B z z B

 
 
Remarque :
Contrairement aux filtres analogiques du premier ordre qui sont toujours
stables, les filtres numériques du premier ordre ne sont pas obligatoirement
stable.
Il faut étudier la valeur de B, qui dépend de a mais surtout de Te, donc de la
fréquence d’échantillonnage. 15
Filtrage numérique

16. Approche par la transformée bilinéaire :
6. Synthèse des filtres numériques
Objectif : A partir d’une équation différentielle (ou d’une Fonction de Transfert
d’un filtre analogique), obtenir l’équation de récurrence ou la transmittance en
z du filtre numérique qui se rapproche du filtre analogique équivalent.
Méthode de la transformée bilinéaire :
 Si on dispose de l’équation différentielle, obtenir la Fonction de
Transfert en analogique H(p) par la transformée de Laplace;
 Remplacer la variable de Laplace p par :
 Si on souhaite obtenir l’équation de récurrence, reprendre la méthode
permettant de passer de la transmittance à l’équation de récurrence vue
précédemment.
1
1
2 1 2 1
. .
1 1
z z
p
Te z Te z


 
 
 
16
Filtrage numérique

17. Approche par la transformée bilinéaire (suite) :
6. Synthèse des filtres numériques
Exemple pour un filtre du 1er ordre du type passe bas :
Soit un filtre analogique ayant pour équation différentielle : ( )
. ( ) ( )
dy t
a y t x t
dt
 
En calculant la transformée de Laplace de cette équation différentielle, il vient :
( ) 1
( )
Y p
X p p a


En faisant la transformation bilinéaire, on obtient :
 
   
. 1
( )
( ) . 2 . . 2
Te z
Y z
X z z aTe aTe


  
Remarque :
Même remarque que pour l’approche par discrétisation de l’équation
différentielle, les filtres numériques du premier ordre ne sont pas
obligatoirement stable. Il faut étudier les racines du dénominateur qui
dépendent de a mais surtout de Te, donc de la fréquence d’échantillonnage.
CONCLUSION : LA STABILITE D’UN FILTRE NUMERIQUE DEPEND
DES PARAMETRES DU FILTRE ANALOGIQUE CORRESPONDANT,
MAIS AUSSI DE LA FREQUENCE D’ECHANTILLONNAGE !! 17
Filtrage numérique

18. 7. Représentation fréquentielle dans le plan de BODE
Comme pour les filtres analogiques, il est possible de tracer les diagrammes
de Bode pour déterminer le gain statique ainsi que les fréquences de coupure,
et la phase.
RAPPEL EN ANALOGIQUE :
On remplace la variable de Laplace p par jω.
Le gain en dB est définit par :
La phase est définit par :
( )
20.log ( ) 20.log
( )
dB
Y j
G H j
X j



 
 
arg ( )
H j
 

EN NUMERIQUE :
On remplace la variable z par , et on trouve
Le gain en dB est définit par :
La phase est définit par :
( )
20.log ( ) 20.log
( )
dB
Y j
G H j
X j



 
 
arg ( )
H j
 

j Te
z e 
 ( )
H j
18
Filtrage numérique

19. Exemple de diagrammes de Bode pour un filtre RIF du premier ordre :
Soit le filtre définit par la relation de récurrence :  
( ) 0,5. ( ) ( 1)
y n x n x n
  
Sa Fonction de Transfert en z (ou transmittance) est :
 
1
( ) 1 1 1
( ) . 1 .
( ) 2 2
Y z z
H z z
X z z
 
 
     
 
La transmittance complexe s’écrit donc :
   
( ) 1 1
( ) . 1 . 1 cos( ) .sin( )
( ) 2 2
j Te
Y j
H j e Te j Te
X j


  


     
Le gain exprimé en dB vaut donc :
La phase vaut donc :
 
   
2 2
1
20.log ( ) 20.log . 1 cos sin
2
dB
G H j Te Te
  
 
   
 
 
2
20.log . 1 cos 2
2
dB
f
G
Fe

 
 
 
 
 
 
 
 
sin 2
arctan
1 cos 2
f
Fe
f
Fe



 
 
 
 
 
 
 
 
 
  
 
 
  19
Filtrage numérique
7. Représentation fréquentielle dans le plan de BODE

20. Exemple de diagrammes de Bode pour un filtre RIF du premier ordre (suite) :
Si l’on prend Fe=1kHz (ωe=6.28krad.s-1), les diagrammes de Bode ont la forme
suivante :
Remarques :
La bande de fréquence
utile va de 0 à Fe/2 pour
respecter le Théorème de
Shannon.
Dans cette bande de
fréquence, le filtre est du
type passe bas.
Graphiquement, la
fréquence de coupure à -
3dB est de 250Hz
(ωc=1571rad.s-1).
Les filtres numériques ont
des pentes supérieures aux
filtres analogiques.
ωc ωe/2
20
Filtrage numérique
7. Représentation fréquentielle dans le plan de BODE

21. ATTENTION :
L’objectif de la synthèse des filtres numériques est de trouver un filtre
numérique qui se rapproche du gabarit du filtre analogique équivalent.
Mais parfois, la fréquence de coupure du filtre numérique est différente du
filtre analogique équivalent.
Il faut par conséquent faire quelques modifications sur le filtre analogique.
(VOIR TD)
21
Filtrage numérique
7. Représentation fréquentielle dans le plan de BODE

22. 8. Equation de récurrence – Implantation dans un calculateur
Structure de base des filtres numériques du type RIF :
x(n-1) x(n-2)
L’opérateur z-1 représente le retard d’un échantillon.
1
0
( ) ( ). ( )
N
k
y n h k x n k


  

h(0).x(n) h(1).x(n-1)
Cette structure est bien celle d’un filtre à Réponse Impulsionnelle Finie.
( ) (0). ( ) (1). ( 1) ... ( 1). ( 1)
y n h x n h x n h N x n N
       
x(n-N+1)
22
Filtrage numérique

23. Structure de base des filtres numériques du type RII :
1
0 1
( ) . ( ) . ( )
M N
n p
k p
y n b x n k a y n p

 
   
 
b0.x(n) z(n) -a1.z(n-1)
23
Filtrage numérique
8. Equation de récurrence – Implantation dans un calculateur

24. Les calculateurs réalisant les filtres numériques sont généralement :
 Des microprocesseurs;
 Des microcontrôleurs;
 Des DSP (Digital Signal Processor).
Les DSP sont des microcontrôleurs spécialisés dans le traitement des signaux.
Ils possèdent des instructions spécifiques (FFT, multiplication, …) intégrées
qui se réalisent dans un temps très court (quelques cycles d’horloges).
L’ensemble des coefficients du filtre numérique est stocké dans la mémoire de
ces composants.
Pour s’assurer de la stabilité des filtres numériques qui dépend des valeurs
des coefficients ak et bk, la représentation des coefficients est très importantes.
Les formats les plus utilisés sont :
Représentation à virgule flottante double précision;
Représentation à virgule flottante simple précision;
Représentation à virgule fixe;
Représentation au format Qn. 24
Filtrage numérique
8. Equation de récurrence – Implantation dans un calculateur