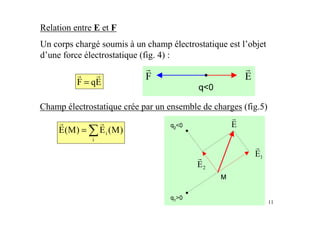
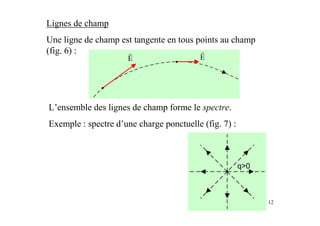
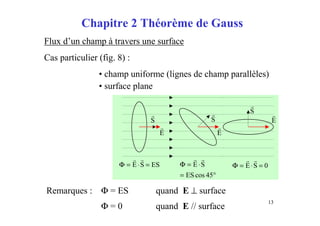
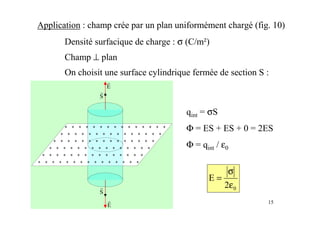
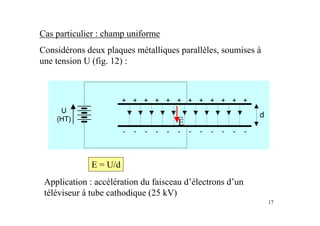
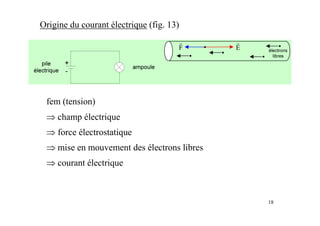
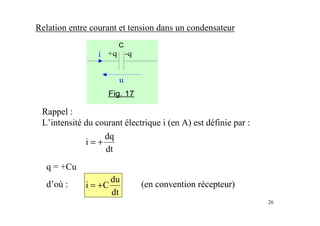
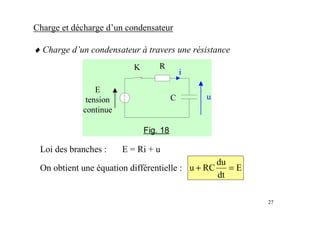
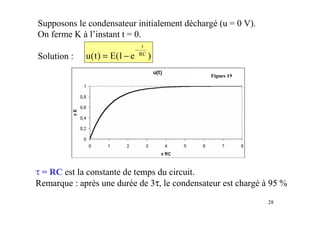
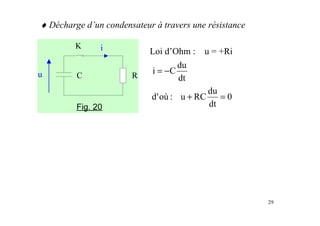
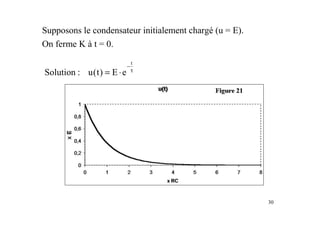
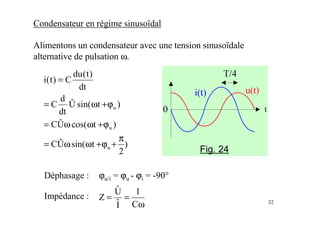
Le document est un module sur l'électricité, axé sur l'électrostatique, les conducteurs et les isolants. Il traite des principes fondamentaux comme les charges électriques, le champ électrostatique, le potentiel électrique, et l'utilisation des condensateurs, incluant des applications et des phénomènes tels que la décharge électrostatique. Les chapitres couvrent également des concepts avancés comme le théorème de Gauss et les associations de condensateurs.

1. 1
Module d’Electricité
2ème partie : Electrostatique
© Fabrice Sincère (version 3.0.1)
http://pagesperso-orange.fr/fabrice.sincere

2. 2
Introduction
• Principaux constituants de la matière :
- protons : charge électrique + e ≈ +1,6 10 -19 coulomb
- neutrons : pas de charge (= neutre)
- électrons : - e
• Un atome a autant d’électrons que de protons : il est
globalement neutre.
• Un corps électrisé (+ ou -) est un corps qui n’est pas neutre.

3. 3
Conducteurs et isolants électriques
Un conducteur métallique possède des électrons libres.
• mouvement d’ensemble d’électrons libres = courant électrique
• l’électrocinétique est l’étude des courants électriques
Un isolant ne possède pas d’électron libre.
L’électrostatique est l’étude de l’électricité statique des corps
électrisés (conducteur ou isolant).

4. 4
Electrisation d’un corps
• Excès d’électrons (-): corps électrisé négativement
• Carence en électrons (+) : ‘ ‘ positivement
- électrisation des isolants : par frottement
Les charges sont immobiles (= statiques)
- électrisation des conducteurs : par influence
Les charges se déplacent jusqu’à atteindre un état
d’équilibre (fig. 1) :
boule en métal
(initialement neutre)
+ + +
On approche une règle en
verre (électrisée par
frottement avec un chiffon)
+
+
+
-
-
-

5. 5
• Application : Machine de Whimshurst (100 kV)

6. 6
Décharge électrostatique
Un courant apparaît quand un corps électrisé se décharge
dans un autre.
Remarque : courant très intense (mais très bref)
tension très élevée >> kV
spectaculaire : foudre >> MV
Exemple : décharge électrostatique d’un corps humain :
• 10 A
• 10 kV
• < 1 µs

7. 7

8. 8
Chapitre 1 Champ électrostatique
Force électrostatique
• Soit deux corps ponctuels de charges q1 et q2 (fig. 2) :
• Sens
- charges de même signe : répulsion
- signe opposé : attraction
1/2F
r
2/1F
r

9. 9
• Intensité : Loi de Coulomb
²r
qq
109
²r
qq
4
1
FFF 21921
0
1/22/1 ⋅≈
πε
===
ε0 ≈ 8,85⋅10-12 F/m : permittivité diélectrique du vide
r : distance (m)
F en newton (N)

10. 10
Champ électrostatique E
Un corps ponctuel de charge q crée un champ électrostatique
radial (fig.3) :
E
r
q < 0 : sens du champ inversé
Intensité (en V/m) :
²r
q
109E 9
⋅≈

11. 11
Relation entre E et F
Un corps chargé soumis à un champ électrostatique est l’objet
d’une force électrostatique (fig. 4) :
Champ électrostatique crée par un ensemble de charges (fig.5)
EqF
rr
=
E
r
F
r
2E
r 1E
r
E
r
∑=
i
i )M(E)M(E
rr

12. 12
Lignes de champ
Une ligne de champ est tangente en tous points au champ
(fig. 6) :
L’ensemble des lignes de champ forme le spectre.
Exemple : spectre d’une charge ponctuelle (fig. 7) :
E
r
E
r
q>0

13. 13
Chapitre 2 Théorème de Gauss
Flux d’un champ à travers une surface
Cas particulier (fig. 8) :
• champ uniforme (lignes de champ parallèles)
• surface plane
Remarques : Φ = ES quand E ⊥ surface
Φ = 0 quand E // surface
S
r
S
r S
r
ESSE =⋅=Φ
rr
°=
⋅=Φ
45cosES
SE
rr
0SE =⋅=Φ
rr
E
r
E
r
E
r

14. 14
Théorème de Gauss
Soit une surface fermée (S) contenant une charge électrique totale
qint (fig. 9) :
ΦΦΦΦ = qint / εεεε0
+
++++++
++
+
+++++ +
+
+
+
+
(S)

15. 15
Application : champ crée par un plan uniformément chargé (fig. 10)
Densité surfacique de charge : σ (C/m²)
Champ ⊥ plan
On choisit une surface cylindrique fermée de section S :
qint = σS
Φ = ES + ES + 0 = 2ES
Φ = qint / ε0
02
E
ε
σ
=
+ + + + + + ++ + + + + + + +
+ + + + + + ++ + + + + + + +
+ + + + + + ++ + + + + + + +
+ + + + + + ++ + + + + + + +
+ + + + + + ++ + + + + + + +
+ + + + + + ++ + + + + + + +
S
r
E
r
S
r
E
r

16. 16
Chapitre 3 Potentiel électrique
A tout point M de l’espace, on peut associer un potentiel électrique
V(M).
Relation entre champ E et différence de potentiel électrique (fig. 11)
Remarques :
dans un circuit électrique : d.d.p. = tension
E est dirigé dans le sens des potentiels décroissants
E ⊥ surface équipotentielle (V=cte)
E = 0 dans un volume équipotentiel
E
r
rd
r
rdEVVdV 12
rr
⋅−=−=

17. 17
Cas particulier : champ uniforme
Considérons deux plaques métalliques parallèles, soumises à
une tension U (fig. 12) :
Application : accélération du faisceau d’électrons d’un
téléviseur à tube cathodique (25 kV)
E
r
E = U/d

18. 18
Origine du courant électrique (fig. 13)
fem (tension)
⇒ champ électrique
⇒ force électrostatique
⇒ mise en mouvement des électrons libres
⇒ courant électrique
E
r
F
r

19. 19
Chapitre 4
Conducteur en équilibre électrostatique
Soit un conducteur plein chargé négativement (fig. 14) :
Charges uniquement en surface.
Champ nul à l’intérieur
(application : cage de Faraday).
Conducteur équipotentiel (V=cte).
A l’extérieur :
lignes de champ ⊥ surface
-
-
-
-
-
-
- -
-
0E
cteV
rr
=
=
E
r

20. 20
Chapitre 5 Le condensateur
Un condensateur est constitué de deux conducteurs (= armatures)
séparés par un isolant (= diélectrique).
Symbole :
U ⇒ champ E ⇒ charges électriques sur les armatures
Q = QA = - QB : charge du condensateur
Capacité électrique (en farad) :
Appliquons une tension U
aux bornes d’un condensateur (fig. 15) :
E
r
C = Q/U

21. 21
εr : permittivité diélectrique relative
≈ 1 pour l’air sec
jusqu’à 10 000 pour les céramiques
S : aire de chaque armature (m²)
d : épaisseur du diélectrique (m)
Capacité d’un condensateur plan
C = εεεε0 εεεεr S/d

22. 22
Champ disruptif (ou rigidité diélectrique)
Au delà d’une certaine intensité (Ed), un isolant devient conducteur.
Exemples :
• Condensateur : U > tension de “claquage”
⇒ destruction du diélectrique
• Air : Ed ≈ 3⋅106 V/m
d = 1 mm : U >> kV ⇒ décharge électrostatique
(bougies d’automobile, briquet piézo-électrique …)

23. 23
d >> m : U >> MV : foudre

24. 24
Chapitre 6 Compléments sur le condensateur
∑=
i
iéq CC
Association de condensateurs
♦ en parallèle
Q1 = C1U
Q2 = C2U
Q = CéqU
Conservation de la charge : Q = Q1 + Q2
Donc : Céq = C1 + C2
En parallèle, les capacités s’additionnent :

25. 25
♦ association en série
∑=
i iéq C
1
C
1
Energie emmagasinée par un condensateur
Un condensateur contient de l’énergie sous forme électromagnétique :
²CU
2
1
W =
avec :
W : énergie en joule (J)
C : capacité (F)
U : tension aux bornes (V)

26. 26
dt
dq
i +=
Relation entre courant et tension dans un condensateur
q = +Cu
d’où :
dt
du
Ci += (en convention récepteur)
Rappel :
L’intensité du courant électrique i (en A) est définie par :

27. 27
Charge et décharge d’un condensateur
♦ Charge d’un condensateur à travers une résistance
Loi des branches : E = Ri + u
On obtient une équation différentielle : E
dt
du
RCu =+

28. 28
Supposons le condensateur initialement déchargé (u = 0 V).
On ferme K à l’instant t = 0.
Solution : )e1(E)t(u RC
t
−
−=
τ = RC est la constante de temps du circuit.
Remarque : après une durée de 3τ, le condensateur est chargé à 95 %

29. 29
dt
du
Ci −=
♦ Décharge d’un condensateur à travers une résistance
Loi d’Ohm : u = +Ri
0
dt
du
RCu:où'd =+

30. 30
Supposons le condensateur initialement chargé (u = E).
On ferme K à t = 0.
τ
−
⋅=
t
eE)t(u:Solution

31. 31
dt
du
CI +=
♦ Charge à courant constant
La charge est linéaire (tension en forme de rampe) :
C
I
t
u
:pente =
∆
∆

32. 32
Condensateur en régime sinusoïdal
Alimentons un condensateur avec une tension sinusoïdale
alternative de pulsation ω.
)
2
tsin(ÛC
)tcos(ÛC
)tsin(Û
dt
d
C
dt
)t(du
C)t(i
u
u
u
π
+ϕ+ωω=
ϕ+ωω=
ϕ+ω=
=
Déphasage : ϕu/i = ϕu - ϕi = -90°
Impédance :
ω
==
C
1
Iˆ
Uˆ
Z