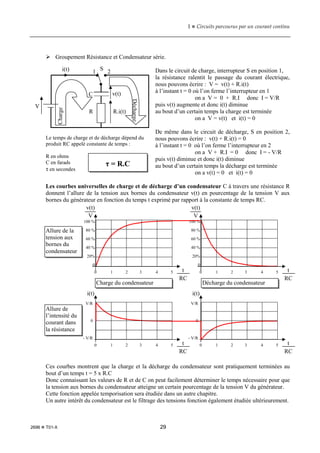
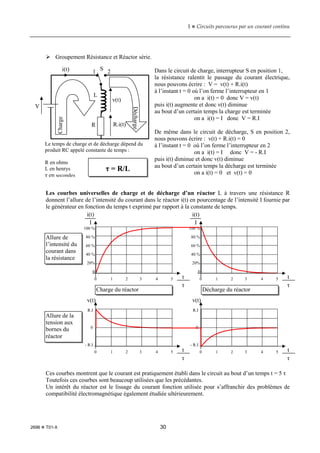
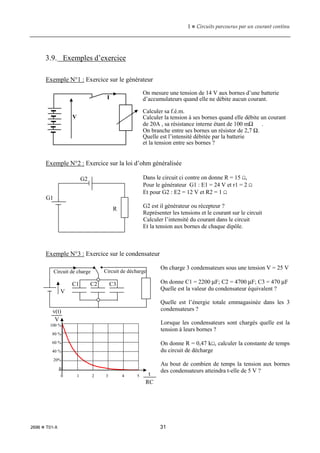
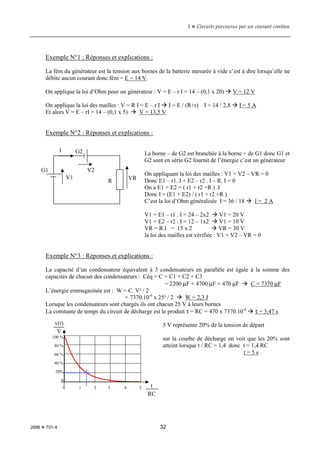
Le document explore les circuits électriques parcourus par un courant continu, incluant des généralités sur les circuits électriques, la définition et la mesure du courant continu, ainsi que des concepts de résistance, tension électrique, et branchement en série et parallèle. Il aborde également l'étude thermique des circuits, les appareils de mesure, et contient des exercices pratiques pour consolider les connaissances acquises. Les principaux principes, tels que la loi d'Ohm et les lois des nœuds, sont présentés de manière méthodique.