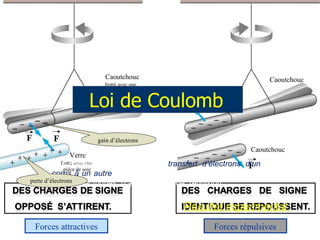
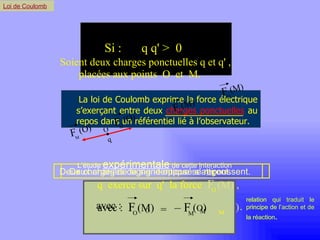
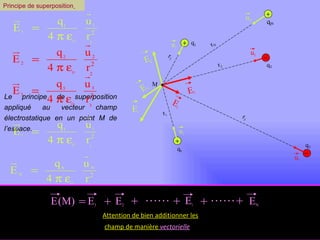
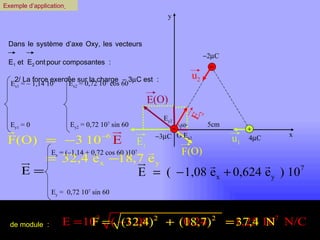
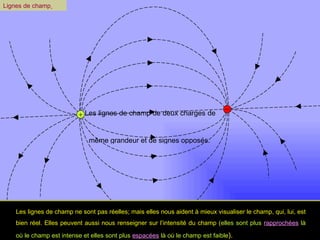
Le document traite de l'électrostatique, en mettant l'accent sur la loi de Coulomb qui décrit les forces entre charges électriques au repos. Il explique comment les charges se manifestent sous forme positive et négative, et présente les caractéristiques et l'interaction des champs électriques générés par ces charges. Enfin, il aborde le principe de superposition pour calculer les forces et les champs résultants entre plusieurs charges.