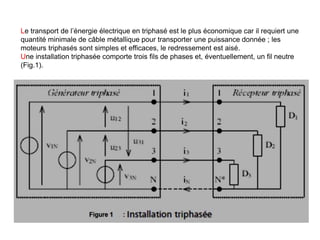
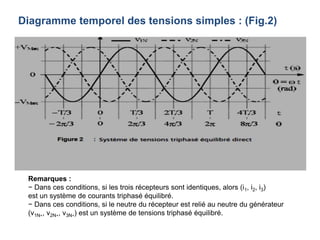
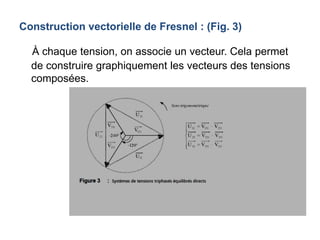
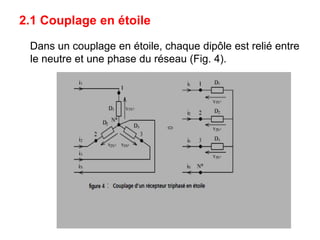
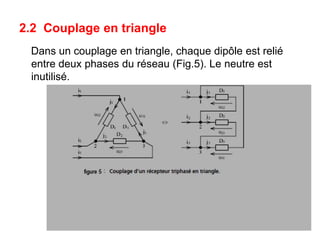
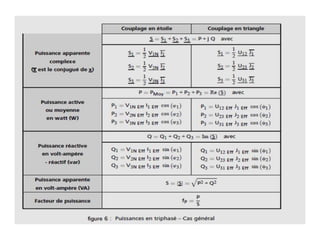
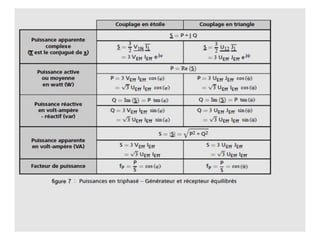
Le document décrit le régime sinusoïdal permanent triphasé, y compris les définitions d'installations triphasées, les tensions simples et composées, ainsi que le couplage en étoile et en triangle. Il aborde également les concepts de système triphasé équilibré et détermine les relations entre les tensions et les courants dans ces systèmes. Enfin, il examine les puissances et le facteur de puissance, notamment les méthodes de mesure utilitaires comme la méthode des deux wattmètres.

1. Chapitre 2 :
RÉGIME SINUSOÏDAL
PERMANENT
TRIPHASÉ

2. 1. INSTALLATION TRIPHASÉE – DÉFINITIONS

3. Le transport de l’énergie électrique en triphasé est le plus économique car il requiert une
quantité minimale de câble métallique pour transporter une puissance donnée ; les
moteurs triphasés sont simples et efficaces, le redressement est aisé.
Une installation triphasée comporte trois fils de phases et, éventuellement, un fil neutre
(Fig.1).

4. • Tensions simples – Tensions composées. Les tensions simples v1N, v2N et v3N sont
prises entre une des phases et le neutre, et les tensions composées u12, u23 et u31
sont prises entre deux phases (voir Fig.1).
• Système triphasé équilibré. Trois grandeurs sinusoïdales de même fréquence,
déphasées entre elles de (2π/3), et ayant même valeur efficace, forment un système
triphasé équilibré.
• Système direct – Système inverse. Le système triphasé (g1, g2, g3) est dit direct
si g3 est en retard d’un angle (2π/3) sur g2 qui est en retard d’un angle (2π/3) sur g1.
Autrement, le système est dit inverse.
• Réseau de distribution électrique. Il est basé sur un système triphasé de tensions.
On peut généralement considérer que (v1N, v2N, v3N) est un système de tensions
triphasé équilibré direct. Il en est de même pour (u12, u23, u31). On a :

5. Diagramme temporel des tensions simples : (Fig.2)
Remarques :
− Dans ces conditions, si les trois récepteurs sont identiques, alors (i1, i2, i3)
est un système de courants triphasé équilibré.
− Dans ces conditions, si le neutre du récepteur est relié au neutre du générateur
(v1N∗, v2N∗, v3N∗) est un système de tensions triphasé équilibré.

6. Exercice : Exprimer la tension composée u12.

7. Construction vectorielle de Fresnel : (Fig. 3)
À chaque tension, on associe un vecteur. Cela permet
de construire graphiquement les vecteurs des tensions
composées.

8. Relations pour un système triphasé équilibré
∀t , v1N + v2N + v3N = 0 ∀t , u12 + u23 + u31 = 0
Umax = √3 Vmax Ueff = √3 Veff
Remarque : Si, pour un réseau, on ne précise pas qu’il s’agit de
tensions simples ou entre phases, il faut considérer qu’il s’agit
des tensions composées. Ainsi un réseau 400 V triphasé 50 Hz
est tel que Ueff = 400 V et Veff = 230 V.
Notation complexe usuelle. Pour simplifier écritures et calculs,
on pose :
a = e j 2π/3 = e−j 4π/3 ⇒ a2 = e j 4π/3 = e−j 2π/3 et a3 = 1
√a = e j π/3 1 − a = √3 e−j π/6 1 − a2 = √3 ej π/6
1 + a + a2 = 0 et a− a2 = +j√3

9. Exercice : Exprimer avec cette notation, V1N, V2N, V3N, U12, U23 et U31.
V1N = Vmax V2N = a2 Vmax et V3N = aVmax
U12 = V1N − V2N = (1 − a2) Vmax
U23 = V2N − V3N = (a2 − a) Vmax = a2(1 − a2) Vmax = a2U12
U31 = V3N − V1N = (a − 1)Vmax = a(1 − a2) Vmax = a U12
Ou encore :
U12 = (1 − a2 )V1N U23 = (1 − a2 )V2N U31 = (1 − a2 )V3N

10. 2. COUPLAGES

11. 2.1 Couplage en étoile
Dans un couplage en étoile, chaque dipôle est relié entre
le neutre et une phase du réseau (Fig. 4).

12. Cas général avec neutre relié
Le point N* étant relié au neutre N du réseau, les tensions appliquées aux bornes des dipôles sont les
tensions simples du réseau, et les courants en ligne sont les mêmes que les courants dans les
récepteurs.
v1N∗ = v1N v2N∗ = v2N v3N∗ = v3N
iN = i1 + i2 + i3
Soit, en complexe :
IN = I1 + I2 + I3 avec I1 = V1N / Z1 I2 = V2N / Z 2 I3 = V3N / Z3
où Z1, Z2 et Z3 sont respectivement les impédances des dipôles D1, D2 et D3.
Récepteur (ou charge) équilibré avec neutre relié
Le récepteur est équilibré si les dipôles sont identiques. Ce qui s’écrit : Z1 = Z2 = Z3
D’où : I1 = V1N / Z1 I2 = a2 V1N / Z2 = a2 I1 I3 = a V1N / Z3 = a I1
IN = I1 + I2 + I3 = I1 (1 + a2 + a) = 0
Remarque : Pour un récepteur équilibré couplé en étoile, le courant dans le neutre est nul.
Neutre non-relié
Si le point N* n’est pas relié au neutre N du réseau, les tensions aux bornes des dipôles dépendent
des dits dipôles. Si les dipôles du récepteur ne sont pas identiques, certains dipôles seront en sous-
tension et d’autres en sur-tension. Dans une installation, pour éviter un fonctionnement incorrect ou un
risque de détérioration d’appareils, le neutre doit toujours être relié, même si la charge est a priori
équilibrée car l’équilibre est précaire par nature, et un incident est toujours possible.

13. 2.2 Couplage en triangle
Dans un couplage en triangle, chaque dipôle est relié
entre deux phases du réseau (Fig.5). Le neutre est
inutilisé.

14. Cas général
Les tensions appliquées aux bornes des dipôles sont les tensions composées du
Réseau, et les courants en ligne sont différents des courants dans les récepteurs.
i1 = j1 − j3 ; i2 = j2 − j1 ; i3 = j3 − j2 et i1 + i2 + i3 = 0
Avec, en complexe :
J1 = U12 / Z1 J2 = U23 / Z2 J3 = U31 / Z3
où Z1, Z2 et Z3 sont respectivement les impédances des dipôles D1, D2 et D3.
Récepteur (ou charge) équilibré
Le récepteur est équilibré si les dipôles sont identiques. Ce qui s’écrit : Z1 = Z2 = Z3
D’où : J1 = U12 / Z1 J2 = a2 U12 / Z2 = a2 J1 J3 = a U12 / Z3 = a J1
J1 + J2 + J3 = J1( 1 + a2 + a) = 0
Exercice : Exprimer les courants dans les lignes I1, I2 et I3.
I1 = J1 − J3 = (1 − a) J1
I2 = J2 − J1 = (a2 − 1)J1 = (1 − a) a2 J1 = (1 − a) J2
I3 = J3 − J2 = (a − a2)J1 = (1 − a) a J1 = (1 − a) J3
Remarque : Pour une charge équilibrée, on a les relations :

15. 3. PUISSANCES – FACTEUR DE PUISSANCE

16. 3.1 Cas général
Les formules (Fig. 6) se déduisent du régime sinusoïdal monophasé,
notamment par application du théorème de Boucherot. Pour un couplage en
étoile, les déphasages des tensions simples v1N, v2N et v3N par rapport aux
courants i1, i2 et i3 sont respectivement notés φ1, φ2 et φ3. Pour un couplage
en triangle, les déphasages des tensions composées u12, u23 et u31 par
rapport aux courants j1, j2 et j3 sont respectivement notés Ψ1, Ψ2 et Ψ3.
3.2 Générateur et récepteur triphasés équilibrés
Les formules (Fig. 7) se déduisent du cas général, sachant que pour un
générateur et un récepteur triphasés équilibrés, on a :
VEff = V1N Eff = V2N Eff = V3N Eff UEff = U12 Eff = U23 Eff = U31 Eff
IEff = I1 Eff = I2 Eff = I3 Eff JEff = J1 Eff = J2 Eff = J3 Eff
φ = φ1 = φ2 = φ3 Ψ = Ψ1= Ψ2 = Ψ3
UEff = √3 Veff JEff = Ieff / √3

19. Exercice : Dans le cas d’un récepteur non équilibré et dont le neutre n’est pas relié,
montrer à partir de la puissance apparente complexe que la mesure de la puissance
active peut s’effectuer à l’aide de la méthode des deux wattmètres.
La puissance fournie par le générateur est :
S = S1 + S2 + S3 = ½ (V1N I*1 + V2N I*2 + V3N I*3)
Comme le neutre n’est pas relié, on a : I1 + I2 + I3 = 0
D’où : S = ½(V1N − V3N) I*1 + ½ (V2N − V3N) I*2 = ½ U13 I*1 + ½ U23 I*2
Finalement, la puissance active se mesure avec deux wattmètres car :
P = Re(S) = Re(1/2 U13 I*1) + Re(1/2 U23 I*2)
= U13 Eff I1 Eff Cos (θ1) + U23 Eff I2 Eff Cos (θ2) = Pu13 i1 + Pu23 i2
Remarque : En régime équilibré, la méthode des deux wattmètres
permet aussi de mesurer la puissance réactive qui est donnée par :
Q = √3 (Pu13 i1 − Pu23 i2)

20. 4. RELEVEMENT DU FACTEUR DE PUISSANCE.

21. En triphasé l’amélioration du
facteur de puissance est
réalisée par 3 condensateurs
qui peuvent être couplés en
étoile ou en triangle.

22. Couplage étoile.
Lorsque le facteur de puissance augmente de
cos initial à cos final le déphasage diminue et la
puissance réactive diminue de :
Q1 = P tan 1 à Q2 = P tan 2.
Cette différence Qc = Q1 - Q2 est fournie par trois
condensateurs de capacités unitaires C, alimentés
sous la tension V, donc de puissance réactive
totale :
Qc = 3 V² C 
C = P ( tan i - tan f )
3 V² 
C = P ( tan i - tan f )
U² 

23. Couplage triangle:
Lorsque le facteur de puissance augmente de
cosinitial à cosfinal le déphasage diminue et la
puissance réactive diminue de :
Q1 = P tan1 à Q2 = P tan2.
Cette différence Qc = Q1 - Q2 est fournie par
trois condensateurs de capacités unitaires C,
alimentés sous la tension U, donc de
puissance réactive totale :
Qc = 3 U² C 
C = P ( tan i - tan f )
3 U² 

24. Remarque :
Le couplage triangle des condensateurs est
plus avantageux car leur capacité est trois
fois plus petite qu’en couplage étoile.
3 x CΔ = C*