Equations différentielles, DUT MP, CM3

Les équations diﬀérentielles
Outils de résolution des équations linéaires du premier ordre
Christophe Palermo
IUT de Montpellier
Département Mesures Physiques
&
Institut d’Electronique du Sud
Université Montpellier 2
Web : http://palermo.wordpress.com
e-mail : cpalermo@um2.fr
twitter: @chr_palermo
Cours du 30 novembre 2010
MONTPELLIER

Plan
1 Résolution des équations homogènes
Recherche de la solution générale
Exemple du circuit RC série
2 Résolution des équations inhomogènes
Lien entre les solutions générales homogènes et inhomogènes
Recherche d’une solution particulière
3 La méthode de Lagrange
Principe
IUT de Montpellier (Mesures Physiques) Les équations diﬀérentielles Nov. 2010 2

Outils et linéarite
Au premier ordre, deux possibilités :
L’équation n’est pas linéaire exemple : ˙y − 3ty2
= 0
L’équation est à variable séparées
L’équation n’est pas à variable séparées (substitution, numérique)
L’équation est linéaire =⇒ deux questions : est-elle
homogène ou inhomogène ?
à coeﬃcients constants ou pas ?

Résolution des équations homogènes
Plan
Principe

Résolution des équations homogènes Recherche de la solution générale
EDL1 homogène
Equation Différentielle Linéaire du 1er ordre (EDL1) homogène :
a(t) · ˙y + b(t) · y = 0 c’est à dire a(t) ·
dy
dt
+ b(t) · y = 0
En manipulant un peu :
dy
y
= −
b(t)
a(t)
· dt
Une EDL1 homogène est à variables séparées !
En intégrant des deux côtés : ln[y(t)] = −
b(t)
a(t)
· dt + B, B ∈ R
Ensuite, deux possibilités :
a(t) et/ou b(t) sont des fonctions : coefficients variables
a(t) = a et b(t) = b sont des constantes : coefficients constants

Résolution des équations homogènes Recherche de la solution générale
Solution générale d’une EDL1 homogène
Pour des coeﬃcients variables :
on pose −
b(t)
a(t)
· dt = F(t) (pratique : constante d’intégration nulle)
donc ln(y) = F(t) + B, B ∈ R
et puis exp [ln y(t)] = y(t) = exp [−F(t) + B] = exp(B) · exp[−F(t)]
On remplace exp(B) par K ∈ R et donc
y(t) = K · exp[−F(t)] , K ∈ R
Pour des coeﬃcients constants :
plus simple : primitive de −b/a avec const. d’intégration nulle : −bt/a
donc −
b
a
· dt = −
b
a
t + B avec B ∈ R
On remplace aussi exp(B) par K ∈ R et donc
y(t) = K · exp −
b
a
t , K ∈ R

Résolution des équations homogènes Exemple du circuit RC série
Un exemple physique : circuit RC série
u
i
E uR
Exemple
Dans un circuit RC série où règne aux bornes d’un condensateur de
capacité 2 mF une tension u constante de 3 V, on coupe le générateur de
tension. Décrire l’évolution de u dans le temps pour une résistance de
1 kΩ.

Analyse de l’énoncé
Exemple
1 kΩ.
Analysons l’énoncé :
Pour la mise en équation :
L’inconnue à déterminer ?
La loi à appliquer ?
Le terme perturbateur ?
Autres informations utiles ?

Exemple
1 kΩ.
L’inconnue à déterminer ? u
La loi à appliquer ?

Exemple
1 kΩ.
La loi à appliquer ? Noeuds et mailles

Exemple
1 kΩ.
La loi à appliquer ? Noeuds et mailles
Le terme perturbateur ? E = 0 V =⇒ équation homogène
La condition initiale : u(0) = 3 V
Les valeurs R = 1000 Ω et C = 2 × 10−3
F

L’équation diﬀérentielle
u
i
E uR
Le courant i est le même dans tout le circuit
Condensateur : Q = Cu =⇒ i = dQ
dt = C ˙u
Résistance : uR = R · i = RC ˙u
Loi des mailles : E = u + uR =⇒ 0 = u + RC ˙u
L’équation diﬀérentielle :
˙u +
u
RC
= 0

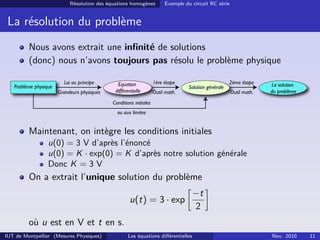
Résolution de l’équation différentielle
du
u
=
−1
RC
· dt (variables séparées et coefficients constantes)
Donc ln u = −
1
RC
· t + B avec B ∈ R
Et finalement
u = K · exp
−t
τ
avec K ∈ R
avec τ = RC = 1000 Ω · 2 × 10−3 F= 2 s
Analyse dimensionnelle : τ est un temps
[τ] = [Ω·F] =
V
A
·
C
V
=
C
A
=
A · s
A
= T
Expression de la solution générale : infinité de solutions

La résolution du problème
Nous avons extrait une inﬁnité de solutions
(donc) nous n’avons toujours pas résolu le problème physique
Equation
différentielle
Solution générale La solution
du problème
Problème physique
Loi ou principe
Grandeurs physiques
1ère étape
Outil math.
Conditions initiales
ou aux limites
2ème étape
Outil math.
Maintenant, on intègre les conditions initiales
u(0) = 3 V d’après l’énoncé
u(0) = K · exp(0) = K d’après notre solution générale
Donc K = 3 V
On a extrait l’unique solution du problème
u(t) = 3 · exp
−t
2
où u est en V et t en s.

Courbes
0
0.5
1
1.5
2
2.5
3
0 2 4 6 8
TensionauxbornesdeC(V)
Temps
3 exp( t/ )
2 exp( t/ )
exp( t/ )
La tension à un instant donné
dépend de la tension initiale !
0
0.2
0.4
0.6
0.8
1
0 2 4 6 8
Tensionnormaliséeu(t)/u(0)
Temps
37 %
5 %
Courbe intégrale : accès à toutes les
solutions en multipliant par un réel

Résolution des équations inhomogènes
Plan
Principe

Résolution des équations inhomogènes Recherche de la solution générale
Solution d’une EDL1 linéaire inhomogène
a(t) · ˙y + b(t) · y = p(t) [= 0] (I)
p(t) = 0 ne change rien à la déﬁnition de la solution
Résoudre une EDL1 inhomogène ⇐⇒ Résoudre une EDL1
homogène :
trouver toutes les solutions de l’équation
une inﬁnité de solutions
Solution générale : écriture avec une constante d’intégration
Solution particulière : une fonction bien précise
Mais il y a une nuance !...
La recherche de la solution générale d’un EDL1 inhomogène n’est pas
aussi simple que celle d’une EDL1 homogène

Exemple
Circuit RC série forcé par une tension E = 3 · cos(4t)
du
dt
+
u
RC
=
3
τ
· cos(4t)
Essayons de procéder comme précédemment :
du
u
= −
1
RC
+ 3 ·
cos(4t)
u
dt
L’équation n’est pas à variables séparées : impossible de continuer
Diﬀérence entre EDL1 linéaire homogène et inhomogène
Homogène : facile de trouver la solution générale
Inhomogène : le plus souvent impossible de déterminer directement
la solution générale

Contre-exemple avec du déjà vu...
La solution générale de ˙y = 2 est une somme
y = 2t + r
la solution générale de ˙y = 0
une solution particulière de ˙y = 2
avec constante d’intégration nulle
La solution générale de ÿ = 2 est une somme
y = t2
+ rt + s
la solution générale de ÿ = 0
une solution particulière de ÿ = 2
avec constante d’intégration nulle
Nous revenons sur cet aspect de somme maintenant !

Une astuce ! ?
Attention :
“contre-exemple” car solution générale facile à trouver
mais les techniques de résolution (somme) s’appliquent
⇒ 1 écriture → 2 approches
Ce que nous venons de voir n’est pas une démonstration
Mais : possibilité de trouver la solution générale de (I) par une
simple addition ?
Possibilité de “d’utiliser” (I) “sous une forme” homogène ?

Une astuce ! ?
Attention :
“contre-exemple” car solution générale facile à trouver
mais les techniques de résolution (somme) s’appliquent
⇒ 1 écriture → 2 approches
Ce que nous venons de voir n’est pas une démonstration
Mais : possibilité de trouver la solution générale de (I) par une
simple addition ?
Possibilité de “d’utiliser” (I) “sous une forme” homogène ?
Maintenant :
Déﬁnition de l’équation homogène associée
Un petit peu d’algèbre linéaire (mais juste un petit peu alors....)

Equation homogène associée
Soit une équation diﬀérentielle du premier ordre inhomogène :
a(t) · ˙y + b(t) · y = p(t) (I)
On lui associe l’équation homogène :
a(t) · ˙y + b(t) · y = 0 (H)
(H) est l’équation homogène associée à (I)
Les solutions de yI de (I) sont liées aux solutions de yH de (H) !

Résolution des équations inhomogènes Lien entre les solutions générales homogènes et inhomogènes
Propriété importante des équations linéaires # 1
s
olutions de (I)
autr
es fonctions
solutio
ns de (H)
autre fonction
linéaire
Somme de deux solutions....
y1(t) −→ 0 est solution de (H) mais pas de (I)
y3(t) −→ p(t) est solution de (I)
Linéarité : y1(t) + y3(t) −→ 0 + p(t) = p(t)
y1(t) + y3(t) est aussi solution (I) !
Pareil pour y1(t) + y2(t) + y8(t) + y3(t)

Propriété importante des équations linéaires # 2
La somme d’une solution particulière yP de (I) et de la solution
générale yH de (H) est solution de (I)
Mais surtout : la somme d’une solution particulière yP de (I) et de la
solution générale yH de (H) est la solution générale de (I)
Théorème (que nous ne démontrerons pas !)
La solution générale yI d’une équation diﬀérentielle linéaire inhomogène
du premier ordre est la somme d’une solution particulière yP de cette
équation (I) et de la solution générale yH de l’équation diﬀérentielle
homogène associée (H), de sorte que :
yI = yH + yP

Synthèse de la recherche de yI
Résoudre une équation inhomogène (I) ⇐⇒ Trouver sa solution
générale
Diﬃculté : pas de séparation de variables (sauf exception)
On utilise ce qui est en fait une astuce de calcul en 4 étapes :
1 Ecrire l’équation homogène associée (H)
2 Résoudre l’équation homogène : solution générale yH de (H)
3 Trouver une solution particulière yP de (I)
4 En déduire la solution générale yI de (I) : yI = yH + yP
Concrètement :
yH est facile à trouver
Mais comment trouver yP ?

Résolution des équations inhomogènes Recherche d’une solution particulière
Recherche de yP
Pour trouver yP
1 On va exprimer yP “à quelque chose près” : quelques inconnues
2 On va injecter yP dans l’équation inhomogène (I) (puisqu’elle en est
une solution)
3 On va ﬁxer les inconnues
Mais comment choisir l’expression de yP de l’étape 1 ?
Méthode du tableau
Méthode de Lagrange

Résolution des équations inhomogènes Recherche d’une solution particulière
La méthode du tableau
Forme de p(t) Forme yP
recommandée
Remarques
k ∈ R α ∈ R
ekt · [A · sin(mt) ekt · [α · sin(mt) • valable pour k = 0
+B · cos(mt)] +β · cos(mt)] et pour A = 0 ou B = 0
exp(kt) · P(t) exp(kt) · Q(t) • valable pour k = 0
• deg(Q) = deg(P)
si k = −b/a
• deg(Q) = 1+deg(P)
si k = −b/a
P1(t) sin(mt) Q1(t) sin(mt) • Faire apparaître sin
+P2(t) cos(mt) +Q2(t) cos(mt) et cos dans yP même si
P1(t) = 0 ou P2(t) = 0
• deg(Q1) = deg(P1)
et deg(Q2) = deg(P2)

Résolution des équations inhomogènes Exemple du circuit RC série
Exemple # 1 : circuit RC série et tension continue
On applique au circuit RC vu précédemment une tension continue
E(t) = E = 3 V alors que le condensateur n’est initialement pas
polarisé. Décrire l’évolution dans le temps de u.
˙u +
1
τ
u =
3
τ
(I)
avec τ = RC = 2 s.
Equation
différentielle
Solution générale La solution
du problème
Problème physique
Loi ou principe
Grandeurs physiques
1ère étape
Outil math.
Conditions initiales
ou aux limites
2ème étape
Outil math.
Ce que nous allons faire :
1 Déterminer la solution générale de (I)
2 Donner la solution du problème

Exemple # 1 : détermination de uI
En 4 étapes :
1 Equation homogène associée (H)
˙u +
1
τ
u = 0 (H)
avec τ = RC = 2 s
2 Equation déjà résolue : uH(t) = K exp −t
2 avec K ∈ R
3 Trouver une solution particulière uP de (I)
1 Forme de uP(t) “à quelque chose près” : uP(t) = α
2 Injection dans (I) : 0 + α/τ = 3/τ
3 α = 3 et donc uP = 3
4 Solution générale uI de (I) :
uI = uH + uP = uI = K · e−t/2
+ 3 avec K ∈ R

Exemple # 1 : Solution du problème
La solution du problème = solution pour laquelle les conditions
initiales sont vériﬁées
Conditions initiales : u(0) = 0 d’après l’énoncé
u(0) = K + 3 d’après la solution générale uI
donc K = −3
La solution du problème :
u(t) = 3 1 − e
−t
2
N. B. : pas de constante d’intégration → solution particulière

Exemple # 1 : courbe de la solution
condition initiale
vers régime
continu (permanent)
Remarques
Modiﬁcation de la solution générale par le terme perturbateur
Conditions initiales : courbe croissante (= cas de la décharge)

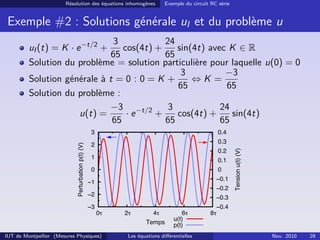
Exemple # 2 : circuit série RC et tension harmonique
On applique au circuit une tension sinusoïdale E(t) = 3 · cos(4t) et
donc :
˙u +
1
τ
· u =
3
τ
· cos(4t)
Même chose que précédemment : uH = K · e−t/2 avec K ∈ R
Seule diﬀérence : détermination de uP
Choix de uP = α cos(4t) + β sin(4t)
Injection dans (I) :
−4α sin(4t) + 4β cos(4t)
˙uP
+1
2 [α cos(4t) + β sin(4t)
˙uP
] = 3
2 cos(4t)
Détermination par identiﬁcation :
(α
2 + 4β) cos(4t) + (−4α + β
2 ) sin(4t) = 3
2 cos(4t) ∀t ∈ R
α
2 + 4β = 3
2
−4α + β
2 = 0
⇔
α = 3/65
β = 24/65
⇔ uP =
3
65
cos(4t) +
24
65
sin(4t)

Exemple #2 : Solutions générale uI et du problème u
uI(t) = K · e−t/2
+
3
65
cos(4t) +
24
65
sin(4t) avec K ∈ R
Solution du problème = solution particulière pour laquelle u(0) = 0
Solution générale à t = 0 : 0 = K +
3
65
⇔ K =
−3
65
Solution du problème :
u(t) =
−3
65
· e−t/2
+
3
65
cos(4t) +
24
65
sin(4t)
−3
−2
−1
0
1
2
3
0τ 2τ 4τ 6τ 8τ
−0.4
−0.3
−0.2
−0.1
0
0.1
0.2
0.3
0.4
Perturbationp(t)(V)
Tensionu(t)(V)
Temps
u(t)
p(t)

La méthode de Lagrange
Plan
Principe

La méthode de Lagrange Principe
La méthode de Lagrange
Aussi appelée méthode de variation de la constante.
Principe de la méthode au premier ordre
On peut trouver une solution particulière yP de (I) en remplaçant la
constante K de la solution générale yH par une fonction du temps K(t)
puis en l’injectant dans (I) pour déterminer K(t).
Avantages :
Pas besoin d’apprendre le tableau par cœur
Peu de risques de se tromper
Inconvénients :
Souvent un petit peu plus longue
Il faut savoir intégrer
Fastidieuse au second ordre

La méthode de Lagrange Exemple du circuit RC série
Retour sur l’exemple # 1
˙u +
1
τ
u =
3
τ
(I)
avec τ = RC = 2 s.
On a uH = K exp(−t/τ), K ∈ R
On pose uP = K(t) · exp(−t/τ) et l’on injecte dans (I) :
˙K(t) · exp(−t/τ) −
1
τ
K(t) · exp(−t/τ)
˙uP
+
1
τ
K(t) · exp(−t/τ)
uP
=
3
τ
Simpliﬁcation systématique : ˙K(t) =
3
τ
exp
t
τ
Constante nulle :
K(t) = 3 exp t
τ ⇐⇒ uP(t) = 3 exp t
τ exp − t
τ = 3
On trouve la même chose qu’avec le tableau

Retour sur l’exemple # 2
˙u +
1
τ
u =
3
τ
cos(4t) (I)
uH = K · exp −t
2 ⇒ uP = K(t) · exp −t
2
On arrive à ˙K(t) = 3
2 cos(4t) exp(t/2) = Re 3
2et/2ej4t
L’intégration de 3
2 · et(1/2+4j) donne 3
2 · 2−16j
65 et(1/2+4j) avec cste nulle
En ne gardant que la partie réelle :
K(t) = 3
65 cos(4t) + 24
65 sin(4t) et/2
Même solution particulière qu’avec le tableau :
uP(t) =
3
65
cos(4t) +
24
65
sin(4t)

Synthèse de résolution d’un problème physique
1 Faire la mise en équation
2 Exprimer la solution générale de l’équation diﬀérentielle
Si elle est inhomogène (I) :
1 Ecrire l’équation homogène associée (H)
2 Résoudre l’équation homogène : solution générale yH de (H)
3 Trouver une solution particulière yP de (I)
1 exprimer yP “à quelque chose près” : quelques inconnues (tableau ou
Lagrange)
2 injecter yP dans l’équation inhomogène (I)
3 ﬁxer les inconnues
4 En déduire la solution générale yI de (I) : yI = yH + yP
3 Prise en compte des conditions initiales dans la solution générale :
solution du problème

Equations différentielles, DUT MP, CM3

Contenu connexe

Tendances

En vedette

Similaire à Equations différentielles, DUT MP, CM3

Plus de Christophe Palermo

Dernier

Equations différentielles, DUT MP, CM3