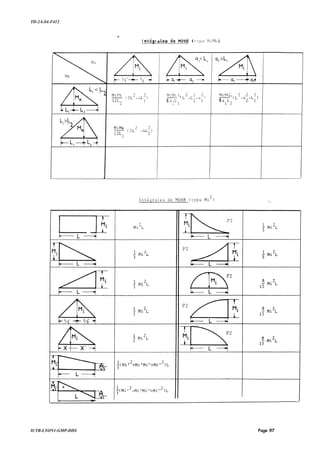
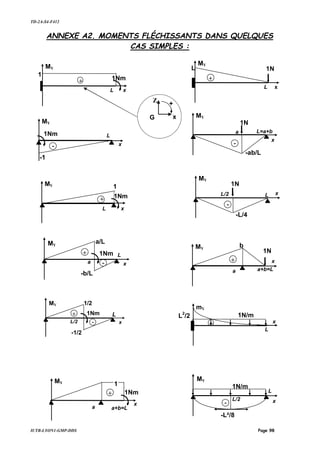
Le document présente des méthodes énergétiques, incluant des problèmes et des corrigés concernant la méthode de Clapeyron, la méthode de Maxwell-Mohr, la méthode des éléments finis et d'autres problématiques liées à la synthèse énergétique. Chaque méthode est accompagnée d'exemples illustrés par des calculs détaillés pour déterminer l'énergie de déformation élastique et des déplacements sous différentes conditions de charge. Les annexes fournissent des informations supplémentaires, notamment des intégrales de Mohr et des cas de moments fléchissants.



![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 4
Pour trouver les efforts normaux s’exercant dans les barres AB et CD, mettons en équilibre
le nœud B :
−=
=
⇒
=+−
=−−
PF
PF
FP
FF
1
2
2
21 2
0
2
2
0
2
2
Après application du principe d’action mutuelle
PN AB
X −= 2PNBC
X =
d’où :
( ) ( ) dx
EA
P
dx
EA
P
W
LL
déf )
2
2
()
2
(
2
00
2 2
∫∫ +
−
=
dx
EA
P
dx
EA
P
W
LL
déf ∫∫ +=
2
0
2
0
2
2
[ ] [ ] 2
0
2
0
2
2
LL
déf x
EA
P
x
EA
P
W +=
2
2
22
L
EA
P
L
EA
P
Wdéf += ( )221
2
2
+=
EA
LP
Wdéf
2 )
Appliquons la méthode de Clapeyron : défext WW =
vBext PW δ
2
1
= ( )221
2
2
+=
EA
LP
Wdéf
En identifiant : ( )221+=
EA
LP
vBδ
3 )
Non, car l’identification implique qu’une seule charge.
Application numérique : P=30kN, L=2m, E=200GPa et A=1cm2
.
( ) ( ) ( ) Nmm
EA
LP
Wdéf 19142221
10010.2002
10.210.10
221
2 3
3232
=+
××
=+= Wdéf=19,142 J
( ) ( ) mm
EA
LP
vB 828,3221
10010.200
10.210.10
221 3
33
=+
×
×
=+=δ •vB=3,83 mm
B
P
45°
X
Y
F2
F1
B
P
L
A
C
P
P 2
P 2
L 2](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-4-320.jpg)
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 5
ROBLÈME N°2
1°) Déterminez l'expression de l'énergie de déformation élastique en
fonction de P, L, A, E et n.
2°) En déduire l'expression du raccourcissement de la barre. Déterminer
l'expression du raccourcissement de la barre pour n=1 et n=2.
Réponses:
)2=(n
8EA
5PL
•L1)=(n
EA
PL
•L
n
1
1
2EA
PL
•L
n
1
1
4EA
LP
W 22
2
def
==
+=
+=
RÈPONSES N°2
1)
La poutre ABC est soumise à de la compression pure : PN AB
x −= PN BC
x −=
( ) ( ) dx
EA
N
dx
AEn
N
W
C
B
BC
x
B
A
AB
x
déf )
2
()
2
(
2
2
2
∫∫ +=
( ) ( ) ( ) ( ) dx
EA
P
dx
AEn
P
dx
EA
N
dx
AEn
N
W
L
L
L
L
L
BC
x
L AB
x
déf )
2
()
2
()
2
()
2
(
2
2
0 2
2
2
2
0 2
2
22
∫∫∫∫
−
+
−
=+=
[ ] [ ]
EA
LP
AEn
LP
x
EA
P
x
AEn
P
dx
EA
P
dx
AEn
P
W
L
L
L
L
L
L
déf
442222
2
2
2
2
2
2
02
2
2
2
2
02
2
+=+=+= ∫∫
P
L/2
B
A
n2
A
A
L/2
C
P
L/2
B
n
2
A
A
L/2
C
A
G x
Z
Y](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-5-320.jpg)

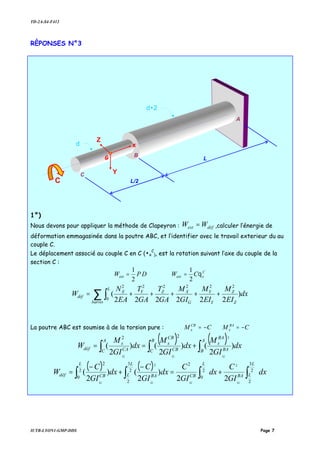

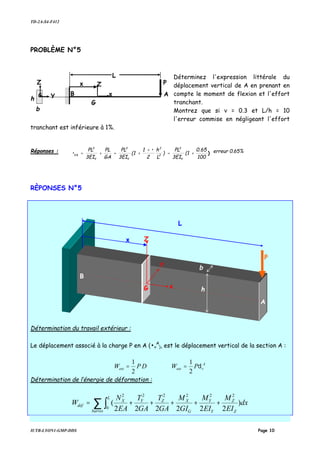
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 11
Nous devons chercher le Torseur de Section en G de la barre AB :
( )
−
−
=ℑ
0
0
0
0
sec XLP
P
tion
G
G
La barre est donc soumise à un effort tranchant constantde B à A : PTZ −= ,
et à un moment de flexion linéaire : ( )XLPMY −=
d’où :
Y
déf
Z
déf
MT
Y
Y
L
Z
L
Y
YZ
L
déf WWdx
EI
M
dx
GA
T
dx
EI
M
GA
T
W +=+=+= ∫∫∫ )
2
()
2
()
22
(
2
0
2
0
22
0
Calculons l’énergie de déformation due à l’effort tranchant :
[ ]
GA
LP
x
GA
P
dx
GA
P
dx
GA
P
dx
GA
T
W
LLL
Z
L
TZ
déf
2222
)
2
(
2
0
2
0
2
0
22
0
===== ∫∫∫
Puis l’énergie de déformation due au moment fléchissant:
( )( ) ( ) ( )
Y
L
Y
L
Y
L
YY
Y
LM
EI
LPxL
EI
P
dxxL
EI
P
dx
EI
xLP
dx
EI
M
W Y
déf
63222
)
2
(
32
0
3
0
2
2
0
22
0
=
−
=−=
−
== ∫∫∫
D’où :
Y
MT
déf
EI
LP
GA
LP
WWW Y
déf
Z
déf
62
322
+=+=
Application numérique : si ν = 0.3 et L/h = 10
+=+=
E
L
GA
I
I
LP
EI
LP
GA
LP
W Y
YY
déf
3262
22322
or
( )υ+
=
12
E
G
( )
+
+=
232
2
1
1
6 L
h
EI
LP
W
Y
déf
υ ( )( )
+
+=
2
32
1,0
2
3,01
1
6 Y
déf
EI
LP
W
( ) ( )
+=+=+= −−
100
65,0
1
6
10.65,01
6
10.5,61
6
32
2
32
3
32
YYY
déf
EI
LP
EI
LP
EI
LP
W
Conclusion :
Y
M
EI
LP
W Y
déf
6
32
= et
100
65,0
6
32
×=
Y
T
EI
LP
W Z
déf](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-11-320.jpg)

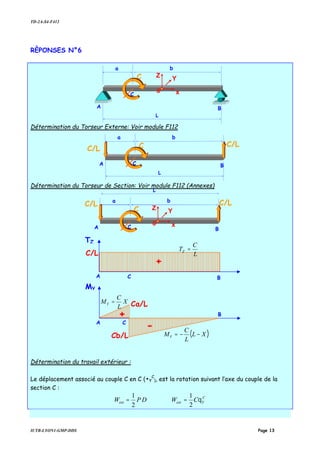



![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 18
Le déplacement généralisé D1 associé à la charge généralisée P1 est le déplacement linéique
dans la direction de P1 de la section A.
Le déplacement généralisé D2 associé à la charge généralisée P2 est le déplacement linéique
dans la direction de P2 de la section B.
[ ] [ ][ ]PfD = ou
=
2
1
2221
1211
2
1
P
P
ff
ff
D
D
2121111 PfPfD +=
2221212 PfPfD +=
La matrice carrée [f] est la matrice de flexibilité de la structure.
Chaque coefficient d’influence fij est calculé par le théorème de Maxwell-Mohr
∑ ∫ ++++=
barres Z
jZiZ
Y
jYiY
G
jXiXjZiZL
0
jYiYjXiX
ij dx)
EI
)m()m(
EI
)m()m(
GI
)m()m(
GA
)t()t(
GA
)t()t(
EA
)n()n(
(f
Pour les déterminer nous devons décomposer l’état initial E0, en deux états unitaires E1 et E2
La poutre ABC, dans les 3 états E0, E1 et E2 n’est soumise qu’à des efforts normaux :
( ) ( )
dx
EA
nn
f
A
C
jXiX
ij ∫=
( ) ( ) ( ) ( ) ( ) ( )
dx
EA
nn
dx
EA
nn
dx
EA
nn
f
A
B
BA
jXiXB
C
CB
jXiXA
C
jXiX
ij ∫∫∫ +==
A
C P2
=
B P1
Etat initial
E0
A
C
B P1=1
A
C
P2=1
B
Etat unitaire
E1
Etat unitaire
E2
E0 • P1×E1+P2×E2](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-18-320.jpg)
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 19
Pour calculer les fij, nous devons chercher les diagrammes des efforts normaux dans les deux
états unitaires :
( ) ( ) ( ) ( ) dx
EA
nn
dx
EA
nn
f
BA
XX
CB
XX
∫∫ +=
1400
800
11
800
0
11
11
dx
EA
dx
EA
f
BACB
∫∫
×
+
×
=
1400
800
800
011
1111
dx
EA
dx
EA
f
BACB
∫∫ +=
1400
800
800
0
11
11
232311
2010.70
4600
3010.70
4800600800
××
×
+
××
×
=+=
ππBACB EAEA
f
5
11 10.345,4 −
=f
( ) ( ) ( ) ( ) dx
EA
dx
EA
nn
f
BACB
XX
∫∫ +=
1400
800
22
800
0
22
22
00
( ) ( ) dx
EA
f
CB
∫
−−
=
800
0
22
22
11
2322
3010.70
4800800
××
×
==
πCBEA
f
5
22 10.616,1 −
=f
( ) ( ) ( ) ( ) dx
EA
n
dx
EA
nn
f
BA
X
CB
XX
∫∫ +=
1400
800
21
800
0
21
12
0
( ) ( ) dx
EA
f
CB
∫
−+
=
800
0
22
12
11
Matrice de flexibilité :
2312
3010.70
4800800
××
×
−=−=
πCBEA
f [ ] 15
616,1616,1
616,1345,4
10 −−
−
−
= mmNf
5
12 10.616,1 −
−=f
Nous en déduisons la matrice des déplacements généralisés :
[ ] [ ][ ]PfD =
=
2
1
2221
1211
2
1
P
P
ff
ff
D
D 35
2
1
10
150
30
616,1616,1
616,1345,4
10
−
−
=
−
D
D
mmD 12,110.15010.616,110.3010.345,4 3535
1 −=×−×= −−
mmD 94,110.15010.616,110.3010.616,1 3535
2 =×+×−= −−
D1 est négatif : le déplacement de la section A s’effectue en sens inverse de celui de
l’application de la charge P1. •A=-1,12 mm
D2 est positif : le déplacement de la section B s’effectue dans le même sens que celui
de l’application de la charge P2. •B=-1,94 mm
800
D=30
d=20
600
A
C
B P1=1
Etat unitaire
E1
G x
Z
Y
1
+
(nX)1
800
D=30
d=20
600
A
C
P2=1
B
Etat unitaire
E2
G x
Z
Y
1-(nX)2](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-19-320.jpg)
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 20
PROBLÈME N°9
Ce problème est le même que le problème 1 qui a été résolu partiellement par la
méthode de CLAPEYRON.
Les barres AB et BC (de même section droite A et de
même matériau) sont articulées en A, B et C. Une
force verticale P1 est appliquée en B. On veut calculer
le déplacement vertical et le déplacement horizontal
du point B par la méthode de MAXWELL-MOHR.
Suggestion : Rajoutez en B une force horizontale
fictive P2 pour calculer le déplacement horizontal.
1°) Déterminer l’expression littérale de la matrice de
flexibilité de la structure (mettre L/EA en facteur).
2°) En déduire l'expression littérale du déplacement
vertical et du déplacement horizontal du point B.
Application numérique : P1=10kN, L=2m, E=200GPa et A=1cm2
. Calculez la valeur du
déplacement vertical et du déplacement horizontal du point B (en mm).
Réponses :
[ ]
−
−+
=
11
1)221(
EA
L
f
2°) ←−=−==↓=
+
== 1mm
EA
PL
D•mm3.83
EA
)PL22(1
D• 2HB1VB
RÈPONSES N°9
La méthode de Maxwell Mohr ou méthode de la charge
unité ne permet de calculer que les déplacements
des points d’applications des charges généralisées
Sur le problème initial qui nous est proposé, nous ne pouvons
donc déterminer que le déplacement vertical du point B.
Nous allons donc créer un problème plus général, dont l’initial
ne sera qu’un cas particulier.
Nous désirons connaître le déplacement horizontal de la
section B. Il est donc nécessaire qu’il existe en B
une charge horizontale.
Appliquons alors en B une charge « fictive » P2 :
A
C
B
P1
45°
L
P2
C
B
P
45°
L
A](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-20-320.jpg)
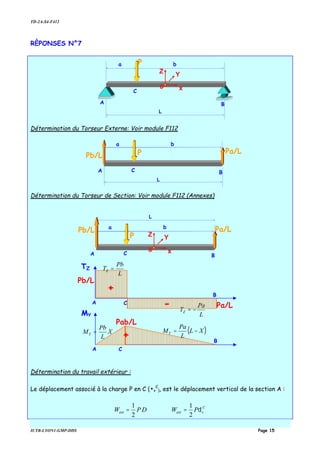
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 22
1°) Expression littérale de la matrice de flexibilité de la structure :
Cherchons les efforts normaux s’exercant sur les deux barres, et pour les deux états
unitaires.
( )
( ) 2
1
1
1
1
+=
−=
BC
AB
x
x
n
n
Etat a
( )
( ) 0
1
2
2
2
=
+=
BC
AB
x
x
n
n
Etat a
Chaque coefficient d’influence fij est calculé par le théorème de Maxwell-Mohr
∑ ∫ ++++=
barres Z
jZiZ
Y
jYiY
G
jXiXjZiZL jYiYjXiX
ij dx
EI
mm
EI
mm
GI
mm
GA
tt
GA
tt
EA
nn
f )
)()()()()()()()()()()()(
(
0
Dans notre cas :
( )( ) ( )( ) ( )( ) ( )( )
dx
EA
nn
dx
EA
nn
dx
EA
nn
dx
EA
nn
dx
EA
nn
f
L j
BC
i
BC
L j
AB
i
AB
C
B
j
BC
i
BC
B
A
j
AB
i
AB
barres
L jXiX
ij
XXXXXXXX
∫∫∫∫∑ ∫ +=+==
2
000
)
)()(
(
( )( ) ( )( ) ( ) ( ) ( )( ) ( )221
2211 2
0
11
0
11
2
0
11
0
11
11 +=+
−−
=+= ∫∫∫∫ EA
L
dx
EA
dx
EA
dx
EA
nn
dx
EA
nn
f
LLL
BCBC
L
ABAB
XXXX
( ) ( ) ( ) ( ) ( ) ( )
EA
L
dx
EA
dx
EA
nn
dx
EA
nn
f
LL
BCBC
L
ABAB
XXXX
=
++
=+= ∫∫∫ 0
22
2
0
22
0
22
22
11
( )( ) ( )( ) ( ) ( ) ( )( )
EA
L
dx
EA
dx
EA
dx
EA
nn
dx
EA
nn
f
LLL
BCBC
L
ABAB
XXXX
−=+
+−
=+= ∫∫∫∫
2
0
21
0
21
2
0
21
0
21
12
0211
[ ]
−
−+
=
11
1)221(
EA
L
f
C
B
P1=1
45°
L
A
Etat unitaire
E1
C
B
45°
L
A
Etat unitaire
E2
P2=1
2
1
-
(nX
AB
)1
+
(nX
BC
)1
1
+
(nX
AB
)2](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-22-320.jpg)
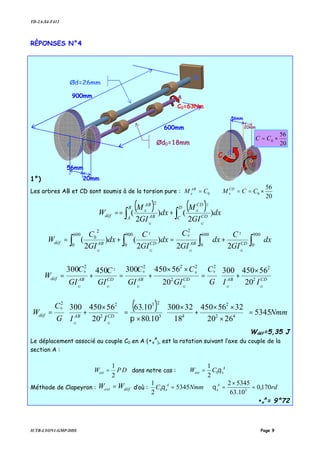
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 23
2°) Expression littérale du déplacement vertical et du déplacement horizontal du
point B :
Dans l’état E0’
[ ] [ ] [ ] '0'0'0 EEE PfD =
'0'0'0
2
1
2
1
11
1)221(
EE
B
h
B
v
E
P
P
EA
L
D
D
−
−+
=
=
δ
δ
Dans l’état E0
−
+
=
−
−+
=
1
)221(
011
1)221(
00
EA
PLP
EA
L
EE
B
h
B
v
δ
δ
Application numérique : P1=10kN, L=2m, E=200GPa et A=1cm2
.
mm
EA
PLB
v 828,3)221(
10010.200
10.210.10
)221( 3
33
=+
×
×
=+=δ •v
B
=3,83 mm
mm
EA
PLB
h 1
10010.200
10.210.10
3
33
−=
×
×
−=−=δ •h
B
=-1 mm
Le déplacement horizontal de B s’effectue en sens inverse de la charge « fictive » P2
PROBLÈME N°10
En appliquant la méthode de MAXWELL-MOHR et en ne tenant
compte que de l’énergie de déformation élastique due au moment
fléchissant, déterminez en fonction de P, L, E et d l’expression
littérale du déplacement vertical et de la rotation en C. En
déduire l’expression littérale de l’énergie de déformation.
Application numérique : P=1425N, E=210 GPa,
L=1m, et d=40mm. Calculez Wdéf en Joules.
Réponses :
4
3
VC
•Ed
P20L
• = 4
2
C
•Ed
P24L
• = 4
23
def
•Ed
P10L
W = 12JWdef =
RÈPONSES N°10
Sur le problème qui nous est proposé, nous ne pouvons déterminer que le déplacement
vertical de la section C.
Nous allons donc créer un problème plus général, dont l’initial ne sera qu’un cas particulier.
Nous désirons connaître la rotation de la section C. Il est donc nécessaire qu’il existe en C
un moment « fictif » porté par l’axe de la rotation cherchée .
Appliquons alors en C un moment « fictif » P2 suivant l’axe Y:
A
P
L L/2
CB
Z
xG
D d= 2
d](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-23-320.jpg)
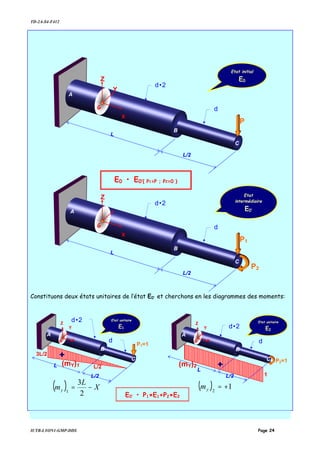

![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 26
Expression littérale du déplacement vertical C.
Dans l’état E0’
[ ] [ ] [ ] '0'0'0 EEE PfD =
'0'0'0
2
1
2221
1211
2
1
EE
C
Y
C
v
E
P
P
ff
ff
D
D
=
=
θ
δ
Dans l’état E0
00
02221
1211
EE
C
Y
C
v
P
ff
ff
=
θ
δ
4
3
11
20
dE
PL
PfC
v
π
δ == •v
C
=20PL3
/E•d4
Expression littérale de la rotation en C.
Dans l’état E0’
[ ] [ ] [ ] '0'0'0 EEE PfD =
'0'0'0
2
1
2221
1211
2
1
EE
C
Y
C
v
E
P
P
ff
ff
D
D
=
=
θ
δ
Dans l’état E0
00
02221
1211
EE
C
Y
C
v
P
ff
ff
=
θ
δ
4
2
21
24
dE
PL
PfC
Y
π
θ == •Y
C
=24PL2
/E•d4
Expression littérale de l’énergie de déformation.
Dans l’état E0’
[ ][ ][ ] [ ]
'0
'0
2
1
2221
1211
21
2
1
2
1
E
E
t
déf
P
P
ff
ff
PPPfPW
==
Dans l’état E0
[ ] 4
32
2
11
2221
1211 10
2
1
0
0
2
1
dE
LP
Pf
P
ff
ff
PWdéf
π
==
=
Application numérique : P=1425N, E=210 GPa, L=1m, et d=40mm.
43
32
4
32
4010.210
100014251010
××
××
==
ππdE
LP
Wdéf Wdéf=12J](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-26-320.jpg)

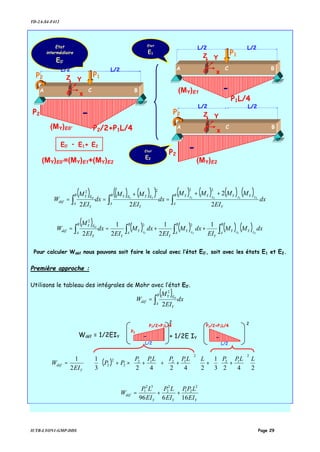




![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 34
Dans l’état E0’
[ ] [ ] [ ] '0'0'0 EEE PfD =
'0'0'0
2
1
2221
1211
2
1
EE
B
v
C
v
E
P
P
ff
ff
D
D
=
=
δ
δ
Or dans l’état hyperstatique, le déplacement vertical de B est nul, P2 s’identifie alors avec la
valeur de la réaction VB de l’état E0.
22
121
22221212 0
f
Pf
PPfPfD B
v −=⇒=+== δ
Calcul des coefficients d’influence dx
EI
mm
f
C
A
Y
jYiY
ij ∫=
)()(
à l’aide des intégrales de Mohr :
Calcul de f11 :
( ) LL
EI
dx
EI
m
f
Y
C
A
Y
Y
×××== ∫
2
2
1
11
3
11)(
YEI
L
f
3
3
11 =
Calcul de f22 :
( ) LL
EI
dx
EI
m
f
Y
B
A
Y
Y
24
3
11)( 2
2
2
22 ×××== ∫ YEI
L
f
3
8 3
22 =
P1
L
B
Z
G x
Y
L
C
P2
A
Etat isostatique
E0’
P1=1
L
B
Z
G x
Y
L
C
A
L
B
Z
G x
Y
L
C
P2=1
A
Etat unitaire
E1
E0’ • P1×E1+P2×E2
Etat unitaire
E2
(mY)2
2L
+
L
L
+
(mY)1
f11 = 1/EIy
L
L
+
2
f22 = 1/EIy
2L
2L
+
2](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-34-320.jpg)
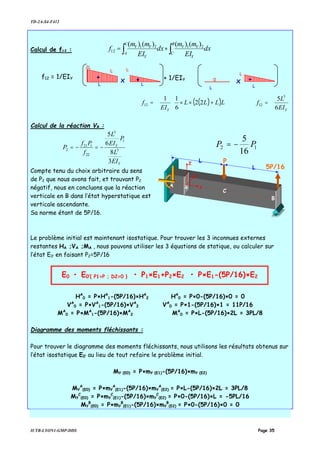
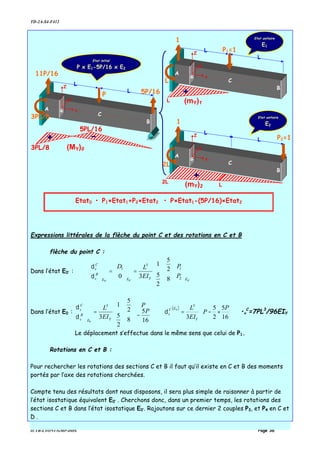
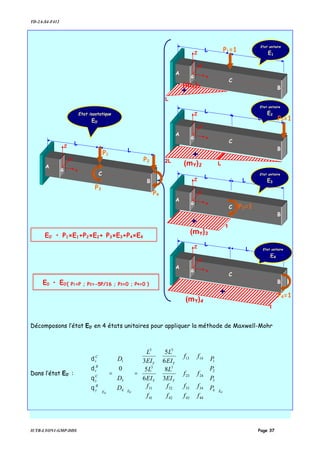


![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 42
Dans l’état E0’
[ ] [ ] [ ] '0'0'0 EEE PfD =
'0'0'0
2
1
2221
1211
2
1
EE
C
AC
A
v
E
P
P
ff
ff
D
D
=
=
δ
δ
Or dans l’état hyperstatique, le déplacement de C dans la direction de P2 est nul, P2
s’identifie alors avec la valeur de la réaction en C de l’état E0 .
22
121
22221212 0
f
Pf
PPfPfD C
AC −=⇒=+== δ
Calcul des coefficients d’influence ∑ ∫ +=
barres Y
jYiYL jXiX
ij dx
EI
mm
EA
nn
f )
)()()()(
(
0
à l’aide des
intégrales de Mohr :
Calcul de f11 :
( ) LL
EI
dx
EI
m
f AB
B
A AB
Y
YY
×××== ∫
2
2
1
11
3
11)(
AB
Y
EI
L
f
3
3
11 =
Calcul de f22 :
( ) ( )
∫∫ +=
C
A AC
X
B
A AB
Y
dx
EA
n
dx
EI
m
f
Y
2
2
2
2
22
)()(
××+
×
××= L
EA
LL
EI
f ACAB
Y
21
1
2
2
3
11 2
2
22 ACAB
EA
L
EI
L
f
Y
2
6
3
22 +=
Etat unitaire
E2
45°
C
L
G x
Z Y
BA
P2=1Etat unitaire
E1
45°
C
L
P1=1
G x
Z Y
BA
E0’ • P1×E1+P2×E2
(mY)2
(mY)1
(nX)2
+
+
-
L 2/2
L
1
f11 = 1/EIy
AB
L
L
+
2
f22 = 1/EIy
AB
L
-
2
+1/EAAC
1
+
2
L 2/2
L 2](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-42-320.jpg)
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 43
Calcul de f12 : dx
EI
mm
f
B
A AB
YY
Y
∫= 21
12
)()(
××−= L
L
L
EI
f AB
Y
2
2
3
11
12 AB
Y
EI
L
f
6
2 3
12 −=
Calcul de la réaction en C :
ACAB
AB
EA
L
EI
L
P
EI
L
f
Pf
P
Y
Y
2
6
6
2
3
1
3
22
121
2
+
−
−=−= 1
2
2
26
1
2
P
AL
I
P
AC
AB
Y
+
=
1°) Tension dans le câble.
Nous avons choisi arbitrairement l’inconnue de l’action en C de telle sorte que le cable AC
soit tendue. Nous trouvons P2 positif : Le cable est donc en traction.
L’effort normal dans le cable est : P
AL
I
N
AC
AB
AC
X
Y
2
26
1
2
+
=
Application numérique : Section AB carrée 60×60, haubanée par un câble AC de diamètre 5 mm. L = 1 m,
E = 200 GPa, P = 3 kN.
NN AC
X 289310.3
5100012
46026
1
2 3
22
4
=
×××
××
+
=
π
NX
AC
=2893 N
2°) Déplacement vertical du point A.
Dans l’état E0’
[ ] [ ] [ ] '0'0'0 EEE PfD =
'0'0'0
2
1
2221
1211
2
1
EE
C
AC
A
v
E
P
P
ff
ff
D
D
=
=
δ
δ
Dans l’état E0
=
2893
3000
0 2221
1211
ff
ffA
vδ
−=−=+= 2893
2
2
3000
3
2893
6
2
3000
3
28933000
333
1211 ABABAB
A
v
YYY
EI
L
EI
L
EI
L
ffδ
mmA
v 473,12893
2
2
3000
6010.2003
121000
43
3
=
−
××
×
=δ •v
A
=1,47 mm
f12 = 1/EIy
AB
L
L
x L
-+
L 2/2](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-43-320.jpg)

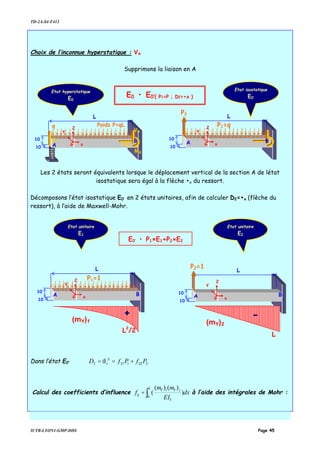


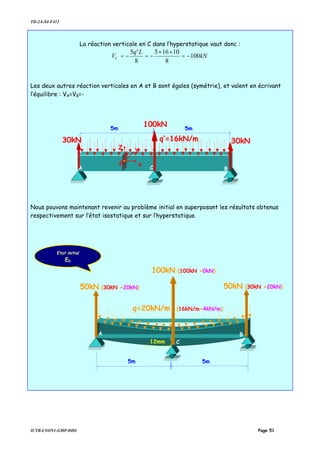

![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 55
Compte tenu des axes de symétrie, pour calculer ces rotations, nous allons raisonner sur le
quart du cadre.
Décomposons l’état isostatique E0’ en 2 états unitaires, afin de calculer D2, à l’aide de
Maxwell-Mohr.
Dans l’état E0’
[ ] [ ] [ ] '0'0'0 EEE PfD =
'0'0'0
2
1
2221
1211
''/'
/
2
1
EE
AA
Z
FC
h
E
P
P
ff
ff
D
D
=
=
θ
δ
22
121
2222121
''/'
2 0
f
Pf
PPfPfD AA
Z −=⇒=+==θ
Calcul des coefficients d’influence ∑ ∫=
barres Z
jZiZL
ij dx
EI
mm
f )
)()(
(
0
à l’aide des intégrales de
Mohr :
P1/2
A’
B
C
L/2=300mm
L/2=300mm
D
E
P1/2
P1/2
P1/2
P1/2
P1/2
P1/2 P1/2
P2 P2
P2 P2
E0 • E0’{ P1=P ; D2=0 }
Etat
isostatique
E0‘
F
A’’
G x
Y
Z](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-55-320.jpg)
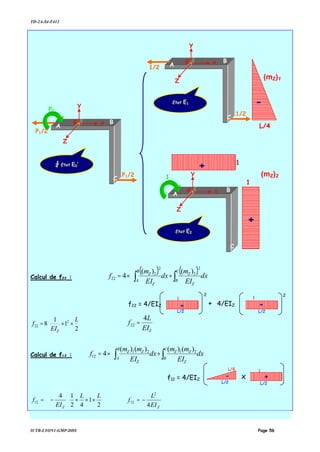

![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 58
Allongement du cadre :
Il nous faut donc déterminer le déplacement relatif des sections C par rapport à F
horizontalement. Nous allons encore travailler avec l’état E0’.
Dans l’état E0’
[ ] [ ] [ ] '0'0'0 EEE PfD =
'0'0'0
2
1
2221
1211
''/'
/
2
1
EE
AA
Z
FC
h
E
P
P
ff
ff
D
D
=
=
θ
δ
212111
/
1 PfPfD FC
h +== δ
Dans l’état E0
+=
16
1211
/ PL
fPfFC
hδ
Nous devons donc calculer f11.
Calcul de f11 :
( ) ( )
+×= ∫∫ dx
EI
m
dx
EI
m
f
C
B
Z
Z
B
A
Z
Z
2
1
2
1
11
)()(
4
×
××=
243
11
4
2
11
LL
EI
f
Z ZEI
L
f
24
3
11 =
×−=
16424
23
/ PL
EI
L
P
EI
L
ZZ
FC
hδ mm
EI
PL
Z
FC
h 26,1
82510.210192
12600505
192
5
33
33
/
=
×××
×××
==δ
Allongement du cadre : •h
C/F
= 1,26 mm
f11 = 4/EIZ
2
L/2
L/4
-](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-58-320.jpg)
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 59
3. MÉTHODE DES ÉLÉMENTS FINIS
PROBLÈME N°17
Considérons la poutre à section droite
variable ci-contre. Le module de YOUNG
E vaut 2.105
MPa, L=1 m. La poutre est
encastrée à ses deux extrémités et est
soumise à une charge axiale P=10kN.
La poutre est discrétisée en trois
éléments poutre et quatre nœuds. L’aire
A vaut 10 mm2
.
1°) Calculez les matrices de rigidité élémentaire des trois éléments sous la forme :
[ ]3
10.4 .
2°) Calculez la matrice de rigidité globale de la structure (sous la forme : [ ]3
10.4 ).
3°) Calculez les déplacements axiaux des nœuds 2 et 3 (en mm), puis les efforts axiaux
sur les nœuds 1 et 4 (en kN).
4°) Calculez le déplacement axial, la déformation axiale et la contrainte (en MPa) au
milieu de l’élément 2.
Réponses:
1°) [ ] [ ] [ ]
−
−
=
−
−
==
11
11
10.4k
22
22
10.4kk 33321 2°)
[ ]
−
−−
−−
−
=
1100
1320
0242
0022
10.4K 3
3°) kN5.2FkN5.7Fmm625.0umm9375.0u x4x132 −=−===
4°) -125MPa-6.25.10mm78125.0u -4
=== σε
RÈPONSES N°17
La poutre droite à section variable est encasrée à ses deux extrémités. La charge P étant
axiale, seules les réactions horizontales existent, et le problème est donc hyperstatique
externe de degré 1.
1 P
L/2 L/2
32
2A
A
L/2
4 x
1 32](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-59-320.jpg)
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 60
1)
Discrétisons la poutre en 3 éléments et 4 nœuds . Dans notre cas les axes locaux et globaux
coïncident. Chaque élément, compte tenu du chargement, n’est soumis qu’à des efforts
normaux. Chaque nœud admet un déplacement u suivant x.
La matrice de rigidité élémentaire en traction-compression [ ]
−
−
11
11
L
EA
=e
k .relie les
efforts d’extrémité de l’élément et les déplacements des nœuds
−
−
=
2
1
2
1
11
11
u
u
L
EA
F
F
e
x
e
x
2A
A
L/2
L/2
L/2
3
1
2
32A
x
2
1
2
4
3
P
2A
A
L/2
1
x
L/2
L/2
2
3
1
2
3
P
4](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-60-320.jpg)
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 61
Calculons les matrices de rigidité élémentaires.
Elément 1 :
[ ]
−
−
11
11
2
L
E2A
=1
k
[ ]
−
−××
11
11
2
1000
1022.10
=
5
1
k
[ ] 22
22
10.4 31
−
−
=k
−
−
=
2
13
1
2
1
1
22
22
10.4
u
u
F
F
x
x
Elément 2 :
[ ]
−
−
11
11
2
L
E2A
=2
k
[ ]
−
−××
11
11
2
1000
1022.10
=
5
2
k
[ ] 22
22
10.4 32
−
−
=k
−
−
=
3
23
2
3
2
2
22
22
10.4
u
u
F
F
x
x
Elément 3 :
[ ]
−
−
11
11
2
L
EA
=3
k
[ ]
−
−×
11
11
2
1000
102.10
=
5
3
k
[ ] 11
11
10.4 33
−
−
=k
−
−
=
4
33
3
4
3
3
11
11
10.4
u
u
F
F
x
x
L/2
1
1
2A x
2
F
1
x1
F
1
x2
2A
L/2
3
2
x
2
F
2
x2
F
2
x3
A
L/2
3
x
4
3
F
3
x3
F
3
x4](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-61-320.jpg)
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 62
2)
Détermination de la matrice de rigidité K de la structure :
Procédons à l’assemblage des 3 matrices de rigidité élémentaires :
3)
D’où : [ ] [ ][ ]DKP =
Appliquons les conditions limites :
La résolution des équations 2 et 3 du système nous permet de trouver
( )
( )
+−=
−=
32
3
32
3
3210.40
2410.4
uu
uuP
625.09375.0 32 mmummu ==
Ces valeurs reportées dans le système nous permettent de résoudre les équations 1 et 4 :
( ) ( )
( ) ( )
−=−=
×−=−=
625,010.410.4
9375,0210.4210.4
3
3
3
4
3
2
3
1
uF
uF
X
X
kNkN 5.2F5.7F x4x1 −=−=
[ ] 22
22
10.4 31
−
−
=k [ ] 22
22
10.4 32
−
−
=k [ ] 11
11
10.4 33
−
−
=k
[ ]
−
−−
−−
−
=
1100
1320
0242
0022
10.4 3
K
−
−−
−−
−
=
4
3
2
1
3
4
3
2
1
1100
1320
0242
0022
10.4
u
u
u
u
F
F
F
F
X
X
X
X
−
−−
−−
−
=
+
0
0
1100
1320
0242
0022
10.4
0 3
23
4
1
u
u
F
P
F
X
X
L/2
x
L/2
L/2
P=10 kN
2,5 kN
7,5 kN](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-62-320.jpg)
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 63
4)
Déterminons les efforts d’extrémités de l’élément 2 :
−
−
=
3
23
2
3
2
2
22
22
10.4
u
u
F
F
x
x
−
−
=
625,0
9375,0
22
22
10.4 3
2
3
2
2
x
x
F
F
−
=
×+×−
×−×
=
−
−
=
2500
2500
625,029375,02
625,029375,02
10.4
625,0
9375,0
22
22
10.4 33
2
3
2
2
x
x
F
F
L’élément est donc soumis à un effort de compression de 2,5 kN
La contrainte vaut pour tout point:
MPa
A
Nx
xx 125
102
2500
−=
×
−
==σ
La déformation associée vaut :
6
5
10.625
10.2
125 −
=
−
==
E
xx
xx
σ
ε
La matrice d’interpolation des déplacements [A] en traction-compression est :
[ ]
−=
L
X
L
X
A 1
[ ][ ]2
)( DAxu =
−=
3
2
1)(
u
u
L
X
L
X
xu
mm
u
uL
u 78125,0
2
1
2
1
)
2
(
3
2
=
=
2A
L/2
3
2
x
2
F
2
x2
F
2
x3
2A
L/2
3
2
x
2
2500 N
2500 N](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-63-320.jpg)
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 64
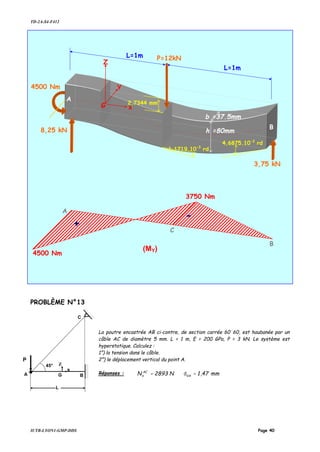
PROBLÈME N°18
Avant d'appliquer la charge horizontale P un jeu "j" existe entre
l'extrémité droite de la poutre et l'appui de droite. La poutre est
modélisée par deux éléments "poutre" et trois nœuds.
1°) Déterminer sous forme littérale les matrices de rigidité
élémentaires et la matrice de rigidité totale en fonction de L, E et
A (mettre 2EA/L en facteur).
2°) E=200GPa, A=5cm2, L=1m et P=100kN. Calculer:
a) Le jeu "j" pour que la poutre arrive juste en contact avec la liaison de droite.
b) Le jeu "j" pour qu'un l'effort de compression de 10kN s'exerce dans l'élément 2.
Réponses:
[ ] [ ] [ ] mm0,175jmm0,25j
110
132
022
L
2EA
K
11
11
L
2EA
k
22
22
L
2EA
k 21
==
−
−−
−
=
−
−
=
−
−
=
RÈPONSES N°18
1°)
Discrétisons la poutre en 2 éléments et 3 nœuds . Dans notre cas les axes locaux et globaux
coïncident. Chaque élément, compte tenu du chargement, n’est soumis qu’à des efforts
normaux. Chaque nœud admet un déplacement u suivant x.
La matrice de rigidité élémentaire en traction-compression [ ]
−
−
11
11
L
EA
=e
k .relie les
efforts d’extrémité de l’élément et les déplacements des nœuds
−
−
=
2
1
2
1
11
11
u
u
L
EA
F
F
e
x
e
x
1
P
L L/2
2
1
2
3
x
j
4A
A
4A
A
L/2
1
x
L
2
1
2
P
3
j](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-64-320.jpg)
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 65
Calculons les matrices de rigidité élémentaires.
Elément 1 :
[ ]
−
−
11
11
L
E4A
=1
k
[ ]
−
−
22
22
L
2EA
=1
k
−
−
=
2
1
1
2
1
1
22
22
L
2EA
u
u
F
F
x
x
Elément 2 :
[ ]
−
−
11
11
2
L
EA
=2
k
[ ]
−
−
11
11
L
A2
=2 E
k
−
−
=
3
2
2
3
2
2
11
11
L
A2
u
uE
F
F
x
x
Détermination de la matrice de rigidité K de la structure :
Procédons à l’assemblage des 2 matrices de rigidité élémentaires :
1°)
D’où : [ ] [ ][ ]DKP =
4
1
xL
2
1
F
1
x1
F
1
x2
A
L/2
x
2
2
3
F
2
x2
F
2
x3
[ ] 22
22
L
2EA1
−
−
=k [ ] 11
11
L
A22
−
−
=
E
k
[ ]
−
−−
−
=
110
132
022
L
A2E
K
−
−−
−
=
3
2
1
3
2
1
110
132
022
L
A2
u
u
u
E
F
F
F
X
X
X](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-65-320.jpg)

![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 67
PROBLÈME N°19
Ce problème est le même que le problème 9 qui a été résolu par la méthode de
MAXWELL-MOHR.
Les barres (1) et (2) de même section droite A et de même
matériau) sont articulées en 1, 2 et 3. Une force verticale
P est appliquée en 2.
1°) Déterminez les matrices de rigidité élémentaire des
deux éléments en fonction de E, A et L et dans le repère
global X,Y. Écrire ces matrices sous la forme :
[ ] [ ]
L
EA
k 1
= [ ] [ ]
L
EA
4
2
k 2
=
2°) Déterminez sous forme littérale la matrice de rigidité
de la structure dans le repère global X, Y. Écrire cette
matrice sous la forme :
[ ] [ ]
L
EA
K =
3°) Calculez (en mm) le déplacement horizontal et le déplacement vertical du noeud 2 pour
A= 1cm², E= 200 GPa, L= 2m, P= 10kN et la valeur (en kN) des réactions sur les nœuds 1 et 3.
4°) Calculez les efforts axiaux dans les éléments 1 et 2.
Réponses :
1°)
[ ]
−
−
=
0000
0101
0000
0101
L
EA
k 1
[ ]
−−
−−
−−
−−
=
1111
1111
1111
1111
L
EA
4
2
k2
2°)
[ ]
−−
−−
−−
−−+−
−
=
4
2
4
2
4
2
4
2
00
4
2
4
2
4
2
4
2
00
4
2
4
2
4
2
4
2
00
4
2
4
2
4
2
)
4
2
1(01
000000
000101
L
EA
K
1
2
X
Y
1
3
2
P
135°
L](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-67-320.jpg)
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 68
3°) mm83,3umm1u 2Y2X −=−=
0F
kN10F
1Y
1X
=
−=
kN10F
kN10F
3Y
3X
=
−=
3°)
kN142.14N
kN10N
BC
x
AB
x
=
−=
RÈPONSES N°19
1°) Matrices de rigidité élémentaire des deux éléments en fonction de E, A et L et
dans le repère global X,Y.
Le problème est à 2 degrés de liberté, uX suivant X et vY suivant Y ( X,Y étant le repère
global )
Elément 1 :
Dans les axes locaux xy
[ ]
−
−
11
11
L
EA
=/xy
1
k
−
−
=
2
1
/xy
1
2
1
1
11
11
L
EA
x
x
x
x
u
u
F
F
Dans les axes globaux XY
[ ]
−
−
0000
0101
0000
0101
L
EA
=/XY
1
k
3
2
P
135°
L
1 X
Y
1
2
2
L
1
1
F
1
x1 F
1
x2
x
y
X
Y](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-68-320.jpg)
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 69
Elément 2 :
Dans les axes locaux xy
[ ]
−
−
11
11
2L
EA
=/xy
2
k
−
−
=
3
2
/xy
2
3
2
2
11
11
2L
EA
x
x
x
x
u
u
F
F
Dans les axes globaux XY
Nous devons calculer [λ] la matrice de
transformation,car pour l’élément 2,
les axes locaux et globaux ne coïncident pas :
[ ]
=
θθ
θθ
λ
sincos00
00sincos
[ ]
°°
°°
=
135sin135cos00
00135sin135cos
λ
[ ]
−
−
=
1100
0011
2
2
λ
[ ] [ ][ ] [ ],
2
,
2
λλ yx
t
YX kk = [ ] 1100
0011
2
2
11
11
2L
EA
10
10
01
01
2
2
,
2
−
−
−
−
−
−
=YXk
[ ] 1100
0011
11
11
10
10
01
01
4L
2EA
,
2
−
−
−
−
−
−
=YXk
[ ] 1100
0011
11
11
11
11
4L
2EA
,
2
−
−
−
−
−
−
=YXk [ ]
−−
−−
−−
−−
=
1111
1111
1111
1111
4
2
,
2
L
EA
k YX
[ ]
−−
−−
−−
−−
=
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
,
2
L
EA
k YX
F
2
x3
F
2
x2
x
y
X
Y
2
3
L 2
2
135°](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-69-320.jpg)
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 70
2°) Matrice de rigidité de la structure dans le repère global X, Y.
Procédons à l’assemblage des 2 matrices de rigidité élémentaires :
3°) Déplacement horizontal et déplacement vertical du noeud 2 :
[ ] [ ][ ]DKP =
XYY
X
Y
X
Y
X
XYY
X
Y
X
Y
X
v
u
v
u
v
u
L
EA
F
F
F
F
F
F
/3
3
2
2
1
1
/3
3
2
2
1
1
4
2
4
2
4
2
4
2
00
4
2
4
2
4
2
4
2
00
4
2
4
2
4
2
4
2
00
4
2
4
2
4
2
)
4
2
1(01
000000
000101
−−
−−
−−
−−+−
−
=
Appliquons les conditions limites :
XY
Y
X
XYY
X
Y
X
v
u
L
EA
F
F
F
F
/
2
2
/3
3
4
1
1
0
0
0
0
4
2
4
2
4
2
4
2
00
4
2
4
2
4
2
4
2
00
4
2
4
2
4
2
4
2
00
4
2
4
2
4
2
)
4
2
1(01
000000
000101
10
0
−−
−−
−−
−−+−
−
=
−
[ ]
−
−
0000
0101
0000
0101
L
EA
=/XY
1
k
[ ]
−−
−−
−−
−−
=
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
,
2
L
EA
k YX
[ ]
−−
−−
−−
−−+−
−
=
4
2
4
2
4
2
4
2
00
4
2
4
2
4
2
4
2
00
4
2
4
2
4
2
4
2
00
4
2
4
2
4
2
)
4
2
1(01
000000
000101
/
L
EA
K XY](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-70-320.jpg)

![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 72
FX1= 10 kN
FY1= 0 kN
FX3= -10 kN
FY3= 10 kN
4°) Efforts axiaux dans les éléments 1 et 2 :
Elément 1 :
Dans les axes locaux xy
[ ]
−
−
11
11
L
EA
=/xy
1
k
−
−
=
2
1
/xy
1
2
1
1
11
11
L
EA
x
x
x
x
u
u
F
F
Les axes locaux et globaux coïncidant :
uX1=ux1 et uX2=ux2
−
=
−
−
−
=
−
−
−
=
4
4
4
/xy
1
2
1
1
10
10
1
0
11
11
01
1
0
11
11
L
EA
x
x
F
F
L’effort normal dans l’élément 1 est un effort axial de compression :
kNNx 101
−=
3
2
10 kN
135°
L
1
X
Y
1
2
10 kN
10 kN
10 kN
2
L
1
1
F
1
x1 F
1
x2
x
y
X
Y
2
L
1
1
10 kN
x
y
10 kN](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-72-320.jpg)
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 73
Elément 2 :
Dans les axes locaux xy
[ ]
−
−
11
11
2L
EA
=/xy
2
k
−
−
=
3
2
/xy
2
3
2
2
11
11
2L
EA
x
x
x
x
u
u
F
F
Les axes locaux et globaux ne coïncident pas
il nous faut calculer :
ux2 et ux3
Utilisons la relation : [ ] [ ][ ] YX
e
yx
e
DD ,, λ=
Avec [λ] trouvée précédement :
[ ]
−
−
=
1100
0011
2
2
λ
−
=
−
−
−
−
=
−
−
=
0
828,2
2
2
0
0
828,3
1
1100
0011
2
2
1100
0011
2
2
3
3
2
2
3
2
Y
X
Y
X
x
x
v
u
v
u
u
u
D’où :
−
−
−
=
−
−
−
=
−
−
=
0
828,2
11
11
10.5
0
828,2
2
2
11
11
2
10
11
11
2L
EA 3
4
3
2
/xy
2
3
2
2
x
x
x
x
u
u
F
F
+
−
=
14140
14140
/xy
2
3
2
2
x
x
F
F
L’effort normal dans l’élément 1 est un effort axial de traction :
kNN BC
x 14,14=
F
2
x3
F
2
x2
x
y
X
Y
2
3
L 2
2
135°
x
y
2
3
L 2
2
14,14 kN
14,14 kN](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-73-320.jpg)

![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 75
1°)
Discrétisons la poutre en 2 éléments et 3 nœuds :
Dans notre cas les axes locaux et globaux coïncident.
Chaque élément, compte tenu du chargement, n’est soumis qu’à un cisaillement de flexion.
Chaque nœud admet un déplacement v suivant Y, et une rotation • suivant Z .
La matrice de rigidité élémentaire en flexion dans le plan XY :
[ ]
−
−−−
−
−
=
22
22
3
4626
612612
2646
612612
LLLL
LL
LLLL
LL
L
EI
k ze
.
Elle relie les efforts d’extrémité de l’élément et les déplacements des nœuds
−
−−−
−
−
=
2
2
1
1
22
22
3
2
2
1
1
4626
612612
2646
612612
z
zz
e
z
e
y
e
z
e
y
v
v
LLLL
LL
LLLL
LL
L
EI
M
F
M
F
θ
θ
P=12kN L=1m
L=1m
FY3
X
Y
Elément 2
Nœud 2
Nœud 3
Nœud 1
Elément 1
Z
FY1
MZ1](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-75-320.jpg)
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 76
Calculons les matrices de rigidité élémentaires.
Elément 1 :
[ ]
−
−−−
−
−
=
22
22
3
1
4626
612612
2646
612612
LLLL
LL
LLLL
LL
L
EI
k z
[ ] ( )
−
−−−
−
−
××
=
−−
4626
612612
2646
612612
12
10.8010.5,3710.200
3339
1
k ; [ ]
−
−−−
−
−
=
4626
612612
2646
612612
10.2,3 51
k
−
−−−
−
−
=
2
2
1
1
5
1
2
1
2
1
1
1
1
4626
612612
2646
612612
10.2,3
z
z
z
y
z
y
v
v
M
F
M
F
θ
θ
Elément 2 :
[ ]
−
−−−
−
−
=
22
22
3
2
4626
612612
2646
612612
LLLL
LL
LLLL
LL
L
EI
k z
[ ]
−
−−−
−
−
=
4626
612612
2646
612612
10.2,3 52
k
−
−−−
−
−
=
3
3
2
2
5
2
3
2
3
2
2
2
2
4626
612612
2646
612612
10.2,3
z
z
z
y
z
y
v
v
M
F
M
F
θ
θ
L=1m
X
Y
Elément 1
Z
F1
Y1
1
2
M1
Z1 F1
Y2
M1
Z2
L=1m
X
Y
Elément 2
Z
F2
Y2
2
3
M2
Z2 F2
Y3
M2
Z3](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-76-320.jpg)
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 77
Détermination de la matrice de rigidité K de la structure :
Procédons à l’assemblage des 2 matrices de rigidité élémentaires :
D’où : [ ] [ ][ ]DKP =
2°)
Appliquons les conditions limites :
La résolution des équations (3), (4),et (6) permet de trouver les déplacements :
mmv 7344.22 −= 3
2 101719.1 −
−=zθ rdz
3
3 106875.4 −
+=θ
[ ]
−
−−−
−
−−−
−
−
=
462600
61261200
268026
612024612
002646
00612612
102.3 5
K
[ ]
−
−−−
−
−
=
4626
612612
2646
612612
10.2,3 52
k[ ]
−
−−−
−
−
=
4626
612612
2646
612612
10.2,3 51
k
−
−−−
−
−−−
−
−
=
3
3
2
2
1
1
5
3
3
2
2
1
1
462600
61261200
268026
612024612
002646
00612612
102.3
Z
Z
Z
Z
Y
Z
Y
Z
Y
v
v
v
M
F
M
F
M
F
θ
θ
θ
( )
( )
( )
( )
( )
( )6
5
4
3
2
1
0
0
0
462600
61261200
268026
612024612
002646
00612612
102.3
0
0
3
2
25
3
1
1
−
−−−
−
−−−
−
−
=
−
Z
Z
Y
Z
Y
v
F
P
M
F
θ
θ](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-77-320.jpg)
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 80
3°)
Flèche :
La matrice d’interpolation des déplacements vaut :
[ ]
+−−+−+−= 2
32
3
3
2
2
2
32
3
3
2
2
23223
1
L
x
L
x
L
x
L
x
L
x
L
x
x
L
x
L
x
A [ ][ ]e
DAxv =)(
+−−+−+−=
3
3
2
2
2
32
3
3
2
2
2
32
3
3
2
2
23223
1)(
z
z
v
v
L
x
L
x
L
x
L
x
L
x
L
x
x
L
x
L
x
xv
θ
θ
Pour 1mLet
2
==
L
x [ ]
−=
8
1
2
1
8
1
2
1
A
mmmv 1.210.1,210
6875.4
0
1719.1
7344.2
8
1
2
1
8
1
2
1
)
2
1
( 33
==
+
−
−
−= −−
Déformation:
La matrice d’interpolation des déformations vaut :
[ ]
+−−+−+−= 232232
6212664126
L
x
LL
x
LL
x
LL
x
L
B
D’où :
6212664126
3
3
2
2
232232
+−−+−+−−=
z
z
xx
v
v
L
x
LL
x
LL
x
LL
x
L
y
θ
θ
ε
Pour : 40mmy1mL
2
±===
L
x
[ ] 3
10
6875.4
0
1719.1
7344.2
101-004.0 −
+
−
−
±=xxε 4
10.3466,2 −
±=xxε
Contrainte :
MPaE xxxx 9.46±== εσ](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-80-320.jpg)
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 81
4. PROBLEMES DE SYNTHESE
PROBLÈME N°21
1ère
partie
Considérons la poutre droite ABC hyperstatique ci-dessus. Toutes les liaisons sont des
articulations. La section droite de la poutre est constante et son moment d’inertie de
flexion est noté YI . Le module de YOUNG du matériau est E. La poutre est soumise à
un couple de flexion P1 appliqué en B.
Prenez comme inconnue hyperstatique la réaction en C (une force P2 dirigée vers le
haut ↑ ).
La méthode de résolution est au choix celle de CASTIGLIANO, ou celle de MAXWELL-
MOHR. Dans les deux méthodes l’énergie de déformation due à l’effort tranchant sera
négligée devant l’énergie de déformation due au moment fléchissant. Si vous choisissez
la méthode de MAXWELL-MOHR écrivez l’expression littérale de la matrice de
flexibilité sous la forme :
[ ] [ ]
YEI
1
f =
Quelle que soit la méthode choisie, CASTIGLIANO ou MAXWWELL-MOHR :
1°) Indiquez quelles sont, selon-vous, les différences essentielles entre les méthodes
de CASTIGLIANO et de MAXWELL-MOHR
2°) Déterminez l’expression littérale de l’inconnue hyperstatique P2 en C en fonction de
P1 et de L en précisant bien son sens ( ↓↑ ou ). Calculez sa valeur numérique en Newton si
P1= 144 Nm et L=1 m.
3°) Déterminez l’expression littérale de la rotation en B en fonction de P1, L, E et IY.
Calculer sa valeur numérique en radian si la section droite a un moment d’inertie IY=
0.25 cm4
et si E = 200 GPa.
2ème
partie
A B
L
P1
x
L/2
L
C
L/2
X
Y
Elément 1 Elément 2
Nœud 1 Nœud 2 Nœud 3](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-81-320.jpg)
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 82
La poutre de la 1ère
partie est discrétisée en deux éléments "poutre" et trois nœuds. La
longueur L vaut 1m, la section droite de la poutre est constante et son moment d’inertie
de flexion Iz vaut 0.25 cm4
. Le module de YOUNG E du matériau vaut 200 GPa. La
poutre est soumise au couple de flexion C= 144 Nm appliqué sur le nœud 2.
Toutes les liaisons sont des articulations.
On donne la matrice de rigidité d’un élément de poutre de longueur L en flexion
dans le plan XY :
[ ]
−
−−−
−
−
=
22
22
3
ze
L4L6L2L6
L612L612
L2L6L4L6
L612L612
L
EI
k
Attention ! La longueur de l’élément 1 est L/2 !
1°) Calculez numériquement (utilisez les unités SI : le mètre et le Newton) les
matrices de rigidité élémentaire des deux éléments dans le repère global X,Y sous la
forme :
[ ] [ ]3
ze
L
EI
k =
2°) Calculez numériquement (utilisez les unités SI : le mètre et le Newton) la matrice
de rigidité de la structure dans le repère global X,Y sous la forme :
[ ] [ ]3
z
L
EI
K =
3°) Calculez, dans le repère global X,Y les rotations en radian des nœuds 1, 2 et 3 et
les réactions en Newton s’exerçant sur les nœuds 1, 2 et 3.
4°) Calculer en mm la flèche de la section droite située au milieu de l’élément 2.
Calculez d’abord numériquement la matrice d’interpolation des déplacements [A],
puis la flèche.
On donne la matrice d’interpolation des déplacements d’un élément de poutre de
longueur L en flexion dans le plan XY :
[ ]
+−−+−+−= 2
32
3
3
2
2
2
32
3
3
2
2
L
x
L
x
L
x2
L
x3
L
x
L
x2
x
L
x2
L
x3
1A
Réponses:
1ère
Partie
1°) La méthode de CASTIGLIANO est analytique, celle de MAXWELL-MOHR matricielle.
2°) ↓−=−= N48
L3
P
P 1
2](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-82-320.jpg)
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 83
3°) rd032.0
EI9
LP
D
I
1
1 ==
2ème
partie
1°)
[ ]
−
−−−
−
−
=
824424
24962496
424824
24962496
500k 1
[ ]
−
−−−
−
−
=
4626
612612
2646
612612
500k 2
2°)
−
−−−
−−
−−−−
−
−
=
3Z
2Z
1Z
3Y
2Y
1Y
0
0
0
462600
61261200
261218424
612181082496
00424824
0024962496
500
0
F
144
F
0
F
θ
θ
θ
3°)
=
3Z
2Z
1Z
420
2124
048
500
0
144
0
θ
θ
θ
rd032.0
rd016.0
2Z
3Z1Z
=
−==
θ
θθ
−
−
−
−−−
−−
−−−−
−
−
=
−=
−=
=
016.0
0
032.0
0
016.0
0
462600
61261200
261218424
612181082496
00424824
0024962496
500
0
48F
144
144F
0
192F
3Y
2Y
1Y
4°)
[ ][ ]e
DA)x(v =
[ ]
+−−+−+−= 2
32
3
3
2
2
2
32
3
3
2
2
L
x
L
x
L
x2
L
x3
L
x
L
x2
x
L
x2
L
x3
1A
1mL
2
L
x ==
[ ]
−=
8
1
2
1
8
1
2
1
A
mm6m006.0
016.0
0
032.0
0
8
1
2
1
8
1
2
1
)
2
1
(v ==
−
−=](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-83-320.jpg)
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 85
[ ] [ ] [ ] '0'0'0 EEE PfD =
'0'0
2
1
32
2
1
26
661
0 EYE
P
P
LL
LL
EI
D
=
ou
YYY
déf
EI
LP
EI
LPP
EI
LP
W
2612
32
2
2
21
2
1
++=
2°) ↓−=−= N
L
P
P 48
3
1
2
3°) rd
EI
LP
D
I
032.0
9
1
1 ==
2ème
partie
1°)
[ ]
−
−−−
−
−
=
824424
24962496
424824
24962496
5001
k [ ]
−
−−−
−
−
=
4626
612612
2646
612612
5002
k
X
Y
Elément 1 Elément 2
Nœud 1
C=144 mN
L/2 L=1m
Nœud 2 Nœud 3
FY2FY1
FY3
•Z1 •Z2
•Z3
IZ=0,25cm4
IZ=0,25cm4
X
Y
Elément 1 Elément 2
Nœud 1
C
A B C
L/2 L
Nœud 2 Nœud 3](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-85-320.jpg)
![TD-2A-S4-F412
IUTB-LYON1-GMP-DDS Page 86
2°)
−
−−−
−−
−−−−
−
−
=
3Z
2Z
1Z
3Y
2Y
1Y
0
0
0
462600
61261200
261218424
612181082496
00424824
0024962496
500
0
F
144
F
0
F
θ
θ
θ
3°)
=
3Z
2Z
1Z
420
2124
048
500
0
144
0
θ
θ
θ
rd032.0
rd016.0
2Z
3Z1Z
=
−==
θ
θθ
−
−
−
−−−
−−
−−−−
−
−
=
−=
−=
=
016.0
0
032.0
0
016.0
0
462600
61261200
261218424
612181082496
00424824
0024962496
500
0
48F
144
144F
0
192F
3Y
2Y
1Y
4°)
[ ][ ]e
DA)x(v = avec [ ]
+−−+−+−= 2
32
3
3
2
2
2
32
3
3
2
2
L
x
L
x
L
x2
L
x3
L
x
L
x2
x
L
x2
L
x3
1A
1mL
2
L
x == [ ]
−=
8
1
2
1
8
1
2
1
A
mm6m006.0
016.0
0
032.0
0
8
1
2
1
8
1
2
1
)
2
1
(v ==
−
−=
[ ]2
500
4626
612612
2646
612612
k=
−
−−−
−
−
[ ]
−
−−−
−
−
=
824424
24962496
424824
24962496
5001
k
[ ]
−
−−−
−−
−−−−
−
−
=
462600
61261200
261218424
612181082496
00424824
0024962496
500K](https://image.slidesharecdn.com/elementsfini-150517232857-lva1-app6891/85/Elements-fini-86-320.jpg)