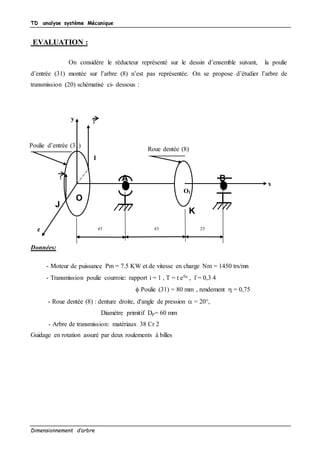
Ce document traite de l'analyse et du dimensionnement d'un arbre d'entrée d'un broyeur à cailloux, en mettant en avant les calculs nécessaires pour déterminer le diamètre approprié et les forces en jeu lors de son utilisation. Il contient des données mécaniques et géométriques, ainsi que des méthodes de modélisation des liaisons et des sollicitations sur l'arbre. L'étude propose également des corrections et des évaluations sur un réducteur associé au système.

1. TD analyse système Mécanique
Dimensionnement d’arbre
APPLICATION 1 :
ARBRE D'ENTRÉE D'UN BROYEUR
Le dessin d’ensemble ci–dessous représente un arbre d'entrée d'un broyeur à cailloux de
grande capacité. Sa modélisation avec ses caractéristiques géométriques sont données sur le schéma
simplifié ci- après.
Les caractéristiques mécaniques sont les suivantes :
Matériau : 55 Si 7.
Re = 600 Mpa ; Rr = 800 Mpa
L'étude qui suit a pour but de calculer le diamètre de cet arbre à partir des méthodes évoquées dans
le cours.
Modélisation de l'arbre d'entrée d'un broyeur
N =750 tr/min ; d = 250 ; 2R = 800 ; P = 200 Kw ; c = 920 ; 4.3esin
f


 = 21.8° ; b =640;  = 10° ; 2r=300
δ δT
t
θ
z
y

2. TD analyse système Mécanique
Dimensionnement d’arbre
Les liaisons entre l’arbre et le bâti en A et B sont réalisées par l'intermédiaire de bagues
lisses, avec jeu. Leur longueur autorise un léger rotulage. On modélisera la liaison pivot de manière
isostatique par l'association d’une rotule et d’une linéaire annulaire.
L’action de la roue sur le pignon en D :
 
 
  
/
/
/
sin sin sin cos cos
cos cos sin cos sin sin
r p
ro pig A
r p
A
D x y z
D r x d y d r z
    

     
   
  
    
 
r ur r
r ur r
Les actions axiales A1, radiales R1, tangentielles T1 s’écrivent :



cos
cossin
sinsin
/1
/1
/1
PR
PR
PR
DT
DR
DA



Travail demandé :
1) Calculer les tensions des courroies.
2) Étudier l'équilibre de l'ensemble (poulie- arbre- roue) et calculer, à l'équilibre, les actions
en A, en B et en K.
3) Représenter les diagrammes des efforts sollicitant cet arbre.
4) Calculer son diamètre mini.
5) On se propose de choisir un autre matériau pour cet arbre tenant compte de
L’encombrement qui exige un diamètre max = 75mm.
Représentation de l’action de la roue sur le pignon en D

3. TD analyse système Mécanique
Dimensionnement d’arbre
x
y
z
A B
I
J
T
t
O
O1
Poulie d’entrée (31)
Roue dentée (8)
K
45 45 25
EVALUATION :
On considère le réducteur représenté sur le dessin d’ensemble suivant, la poulie
d’entrée (31) montée sur l’arbre (8) n’est pas représentée. On se propose d’étudier l’arbre de
transmission (20) schématisé ci- dessous :
Données:
- Moteur de puissance Pm = 7.5 KW et de vitesse en charge Nm = 1450 trs/mn
- Transmission poulie courroie: rapport i = 1 , T = t ef , f = 0,3 4
 Poulie (31) = 80 mm , rendement  = 0,75
- Roue dentée (8) : denture droite, d'angle de pression  = 20°,
Diamètre primitif Dp= 60 mm
- Arbre de transmission: matériaux 38 Cr 2
Guidage en rotation assuré par deux roulements à billes

4. TD analyse système Mécanique
Dimensionnement d’arbre
Correction de l’application : ARBRE D'ENTRÉE D'UN BROYEUR
Recherche des sollicitations dans l’arbres
Calcul des efforts extérieurs
L’arbre isolé est soumis à :
 L’action de la courroie : Si on se place à la limite du glissement.
.
sin( )
.
sin( )
.( )
.
.( 1)
f
f
Cm R T t
Cm
T t e t
R e




 
  

où mNPCm .2546
750.
30.10.200
.
30.
3




Nt 2652
4.2.4.0
2546 
T=2652.3.4=9017N ; Cm= 2546 N.m; t = 2652N ; T = 9017N
Torseur de la courroie sur la poulie :
 /
0
( ).cos( ) 0
( ).sin( ) 0
c p c
c
Cm
T t
T t
 

 
 
   
   
 /
0 0
( ).cos( ) 0 ( ).cos( ) 0
( ).sin( ) 0 ( ).sin( ) 0
c p A
A
Cm c
T t T t
T t T t
  
 
       
      
            
                
 /
0
( ).cos( ) .( ).sin( )
( ).sin( ) .( ).cos( )
c p c
A
Cm
T t c T t
T t c T t
  
 
 
 
    
     
 L’action de la roue sur le pignon en D:
 
/ /
/ / /
/ /
.sin( ).sin( ) . .cos( )
.sin( ).cos( ) . .cos( )
.cos( ) .( .sin( ).cos( ) .sin( ).sin( ))
R p R p
ro pig R p R pA
R p R p A
D D r
D D d
D D d r
  
   
    
 
 
   
 
  
Les actions axiales : 1 / sin( ).sin( )R pA D  
Les actions radiales : 1 / sin( ).cos( )R pB D   
Les actions tangentielles : 1 / cos( )R pT D  
 L’action de la liaison en A (rotule unilatérale) :
 /
0
0
0
A
ba arb Ac
A A
X
Y
Z

 
 
  
 
 
 L’action de la liaison en B (linéaire annulaire) :

5. TD analyse système Mécanique
Dimensionnement d’arbre
 /
0 0
0
0
ba arb BB
B B
Y
Z

 
 
  
 
 
 /
0 0 0
0 0
0 0
ba arb B BA
B B A
b
Y Y
Z Z

      
     
       
     
      
 /
0 0
.
.
ba arb B BA
B B A
Y Z b
Z Y b

 
 
  
  
 Appliquons le principe fondamental de la statique au point A :
/
/
/
/
/
/
0 .sin( ).sin( ) 0 0
.( ) . .cos( ) 0 0 0
( ).cos( ) .sin( ).cos( ) 0
.( ).sin( ) . .cos( ) 0 . 0
( ).sin( ) .cos( ) 0
.( ).cos( ) .( .sin( ).cos(
R p A
R p
R p A B
R p B
R p A B
R p
D X
R T t D r
T t D Y Y
c T t D d b Z
T t D Z Z
c T t D d
 

  
 
 
  
   
    
     
    
     
   ) .sin( ).sin( )) . 0Br bY 
 
 
 
 
 
 
 
 
 
    
Que l’on peut écrire sous le forme suivante:
1
1
1
1
1
1 1
(1) 0 0
(2) .( ) . 0
(3) ( ).cos( ) 0
(4) .( ).sin( ) . . 0
(5) ( ).sin( ) 0
(6) .( ).cos( ) ( . . ) . 0
A
A B
B
A B
B
A X
R T t r T
T t R Y Y
c T t d T b Z
T t T Z Z
c T t d R r A bY




   
    
       
 
    
      
 
       
/ .sin( ).sin( )
. : 18063.sin(20 ).sin(21 .8)
2294
A R p
A
A
X D
A N X
X N
  
   
 
1
1 2294
AA X
A N
 

1 /
1
1
.sin( ).cos( )
. : 18063.sin(20 ).cos(21 .8)
5736
R pR D
A N R
R N
  
   
 
1 /
1
1
.cos( )
. : 16974
16974
R pT D
A N T
T N
 
 
 

6. TD analyse système Mécanique
Dimensionnement d’arbre
1
3 3
3
.( ).sin( ) .
920.10 .(9017 2652).sin(10 ) 250.10 .16974
. :
640.10
5042
B
B
B
c T t d T
Z
b
A N Z
Z N

 

 

  

 
1 1
3 3 3
3
.( ).cos( ) . .
920.10 .(9017 2652).cos(10 ) 150.10 .2294 250.10 .( 5736)
. :
640.10
14816
B
B
B
c T t r A d R
Y
b
A N Y
Y N

  

  

    


1( ).cos( )
. : (9017 2652).cos(10 ) 5736 14816
2412
A B
A
A
Y T t R Y
A N Y
Y N
   
    

1( ).sin( )
. : (9017 2652).sin(10 ) 16974 5042
23121
A B
A
A
Z T t T Z
A N Z
Z N
   
    

Le calcul statique donne :
/
1
1
1
18063
2294
5736
16974
2294
2517
23121
5042
14816
R p
A
A
A
B
B
D N
A N
R N
T N
X N
Y N
Z N
Z N
Y N


 
 
 


 

Modélisation en poutre :
XA
YA
ZA
y
z
A
B
YA
ZB
T1
R1
A1

7. TD analyse système Mécanique
Dimensionnement d’arbre
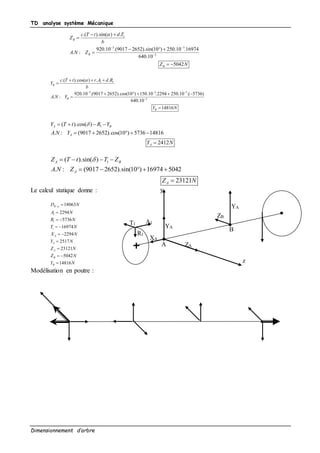
Recherche des efforts de cohésion :
 Zone [E A] 0 x d 
2 2
2 2
2294 2546 .
5736 16974.
16974 5736 344
17917
0, 344 .
250 , 4381 .
t
y fy
z fz
y z
f
f fy fz
f
N N M N m
T N M x
T N M x
T T T N
Pour x M N m
M M M
Pour x d mm M N m
  
 
   
  
 
   
  
 Zone [A B] 0 x b  :
2 2
2 2
0 2546 .
14816 11492 3324 5042.( ) 1105.( )
6147 14816.( ) 11492.( )
6988
0, 4381 .
640 , 3233 .
t
y fy
z fz
y z
f
f fy fz
f
N N M N m
T N M b x c x
T N M b x c x
T T T N
Pour x M N m
M M M
Pour x b mm M N m
 
      
      
  
 
   
  
 Zone [B C] 0 ( )x c b   :
2 2
2 2
0 2546 .
11492 1105.( )
1105 11492.( )
11545
0, 3233 .
, 0 .
t
y fy
z fz
y z
f
f fy fz
f
N N M N m
T N M c b x
T N M c b x
T T T N
Pour x M N m
M M M
Pour x c b M N m
 
     
     
  
 
   
  
E A B
N(N)
2294
T(N)
17917
11545
6988
Mt(Nm)
2546
Mf (Nm)
4381
3233

8. TD analyse système Mécanique
Dimensionnement d’arbre
Les diagrammes représentatifs de l’évolution des différentes sollicitations sont donnés ci-dessous :
D’après les diagrammes représentatifs des différents sollicitations, on remarque que la section la
plus sollicitée est celle d’abscisse x=d où max
max
4381 .
2546 .
f
t
M N m
M N m



Matériau 55 si7
Re 600
800
MPa
Rr MPa



 Calcul de diamètre :
max
Re 600
120 .
5 5
adm PeR MPa    
 Critère de Vom Mises :
max max
2
max 3. ²
com adm
com
 
  

 
sachant que :
3 3
32. 16.
. .
f f t
M M M
IGz d d

 

  
2 2 2 2 2
3 3 3
2 2
3
.
3
2 23
32. 16 32
3. ² ( ) ( ) . 4.
. . .
32
. 4.
.
32.10
. : . (4381) 4.(2546)
.120
82.9
83
f
t f t Max
f t
Max adm
M
M M M
d d d
d M M
A N d
d mm
soit d mm
  
  
 

     
  
 

