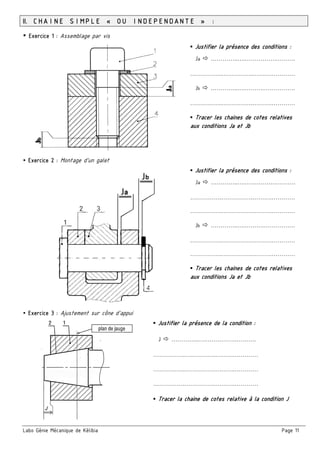
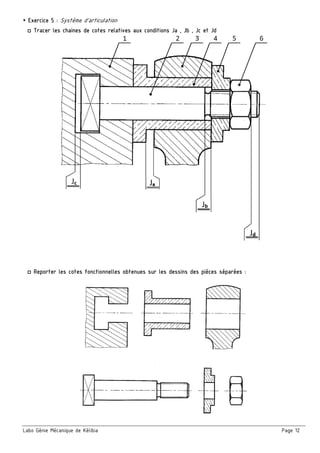
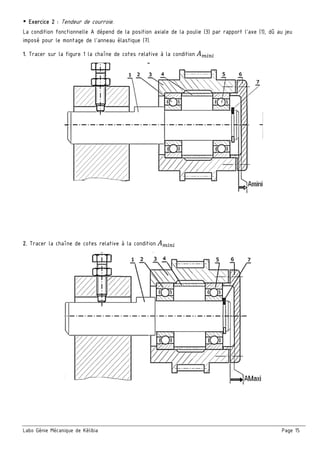
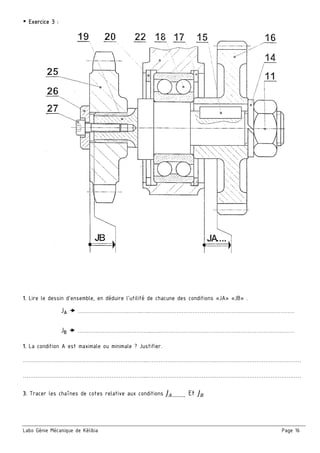
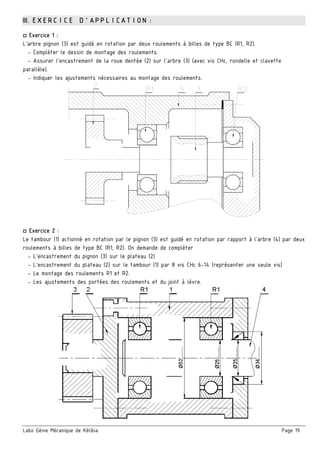
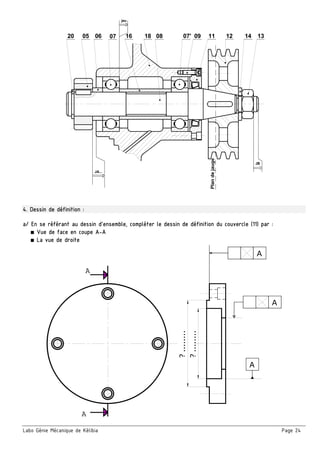
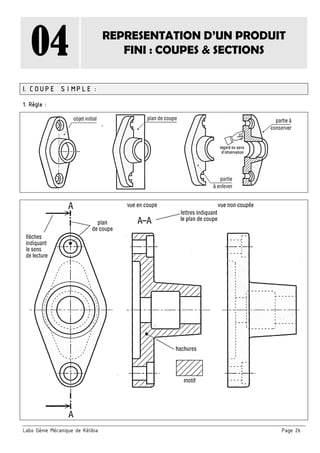
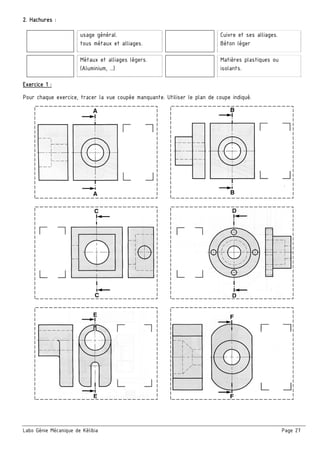
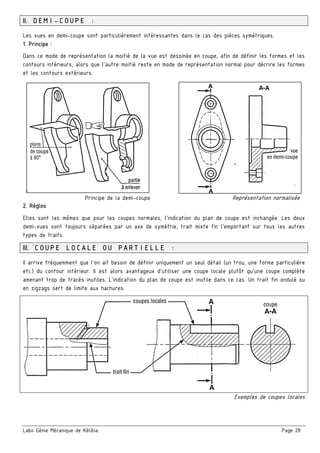
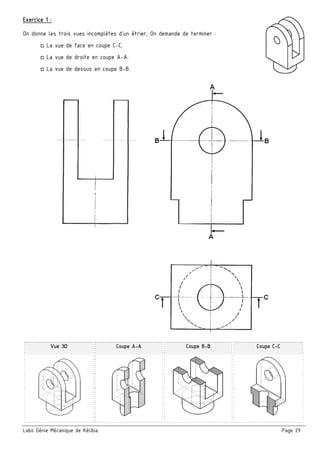
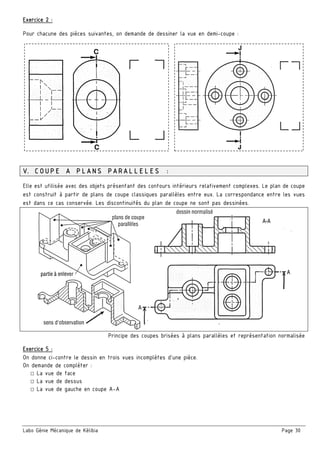
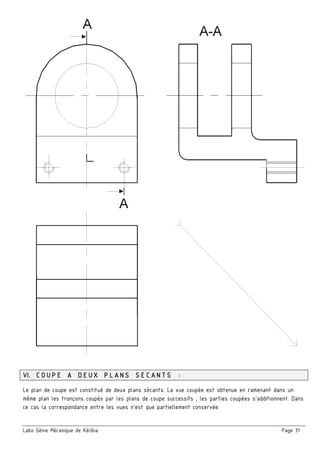
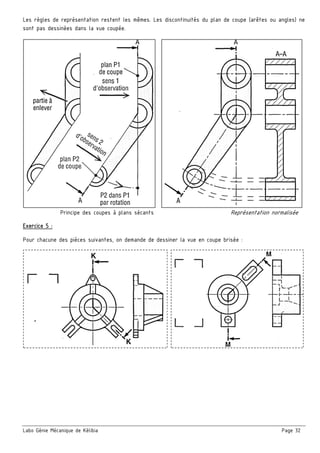
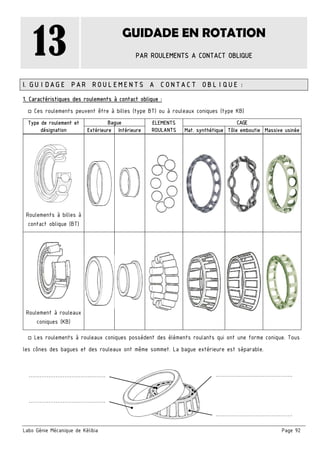
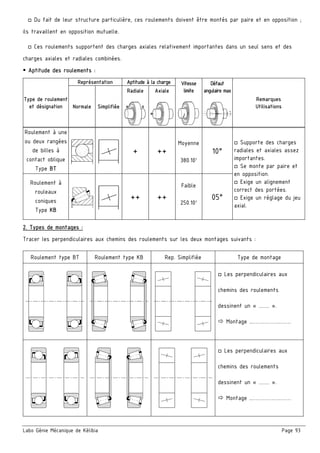
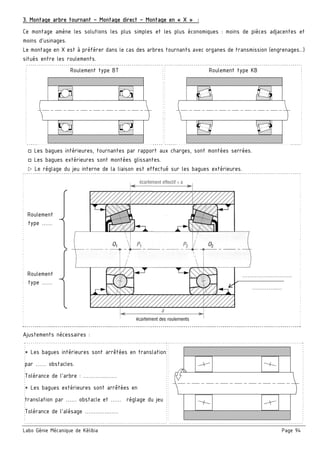
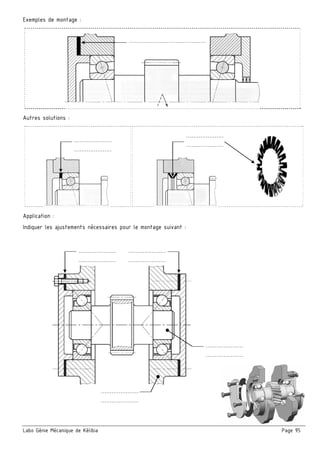
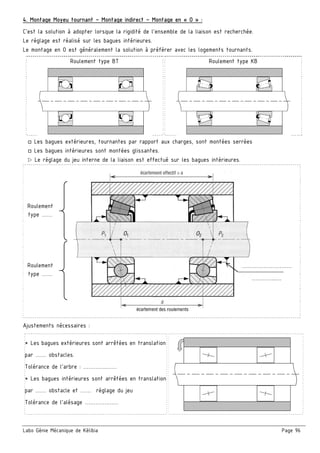
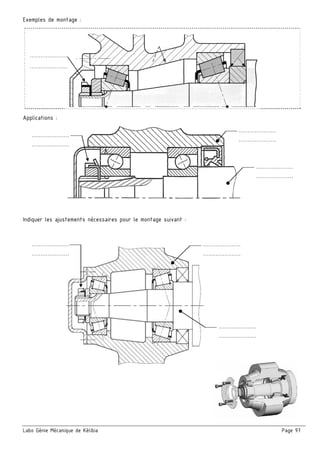
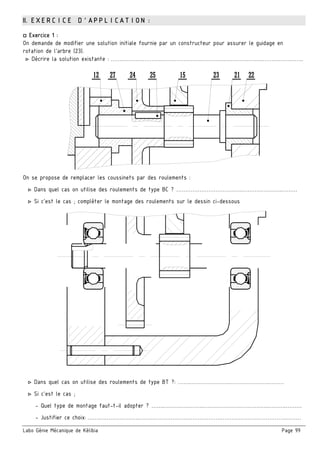
Le document présente un ensemble de chapitres concernant l'analyse fonctionnelle, la cotation fonctionnelle et les mécanismes d'entraînement, notamment dans le cadre de la bouchonnage de flacons. Il aborde des concepts tels que les tolérances dimensionnelles, les ajustements nécessaires, et les principes de fonctionnement de divers systèmes mécaniques. Des exercices pratiques et des schémas illustrés sont inclus pour soutenir l'apprentissage des notions théoriques.
















![Labo Génie Mécanique de Kélibia Page 23
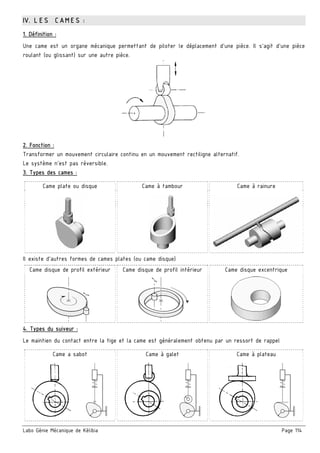
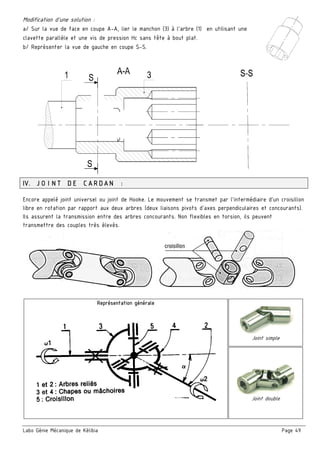
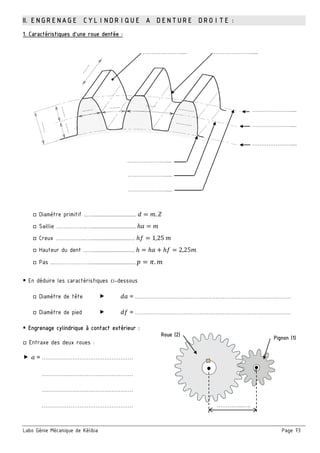
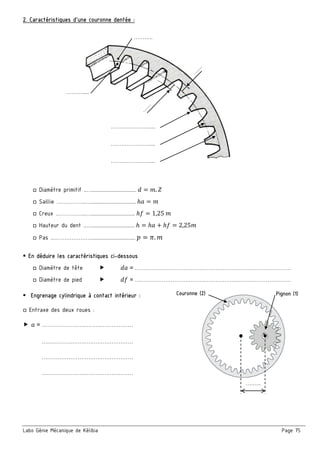
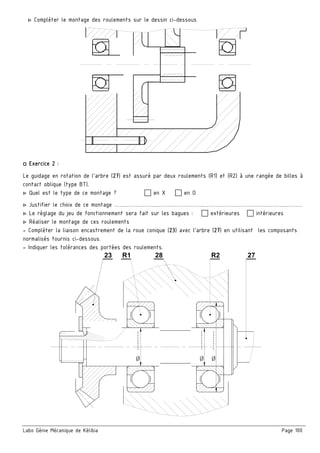
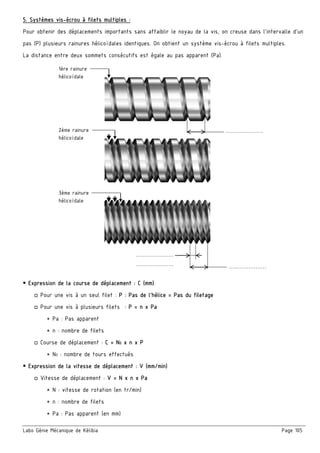
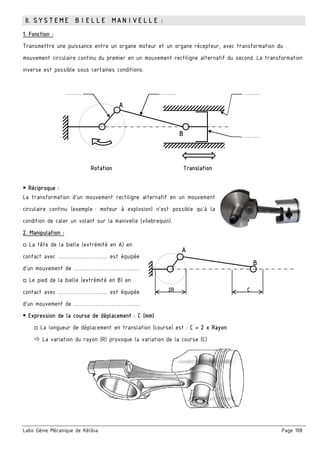
2. Etude cinématique du mécanisme :
a/ Calculer le rapport global rg
………………………….……..………………………..………………………………….………………………………….
■ En déduire la vitesse de rotation du moteur Nm
………………………….……..………………………..………………………………….………………………………….
b/ Calculer le rendement global ηg
………………………….……..………………………..………………………………….………………………………….
■ En déduire la puissance de l’arbre moteur Pm
………………………….……..………………………..………………………………….………………………………….
…………………………………………………………………………………………………………………………………
c/ En déduire le couple du moteur Cm
………………………….……..………………………..………………………………….………………………………….
…………………………………………………………………………………………………………………………………
d/ choisir le moteur qui convient
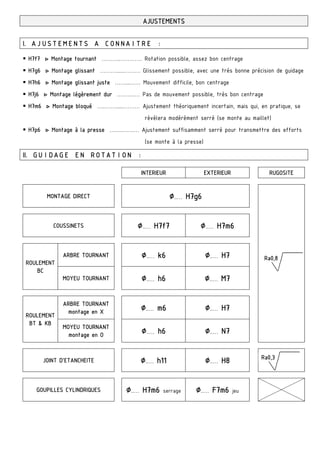
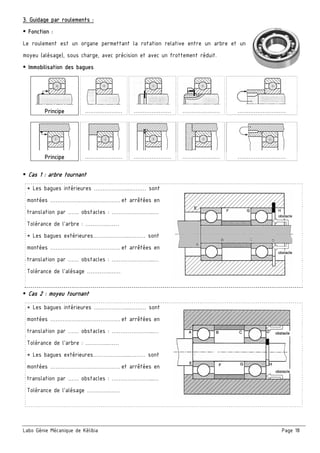
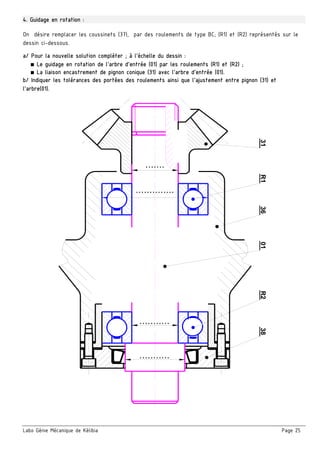
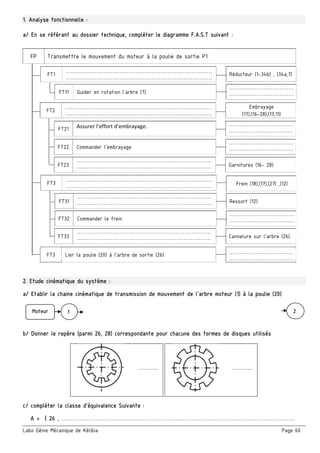
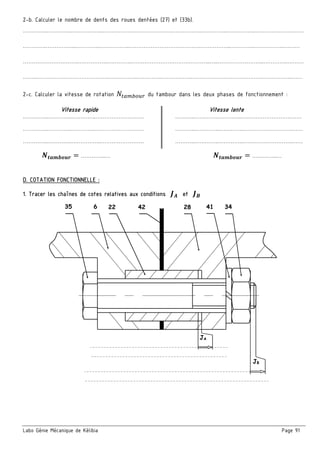
3. Cotation fonctionnelle :
a/ justifier la présence des cotes condition JA et JB
■ JA ……………..…………………………………..….………….
■ JB ……………..…………………………………….………….
b/ La condition JA est-elle mini ou maxi? Justifier.
………………………….……..………………………..………………………………….………………………………….
…………………………………………………………………………………………………………………………………
c/ Tracer les chaînes de cotes installant la condition (JA………) et (JB).
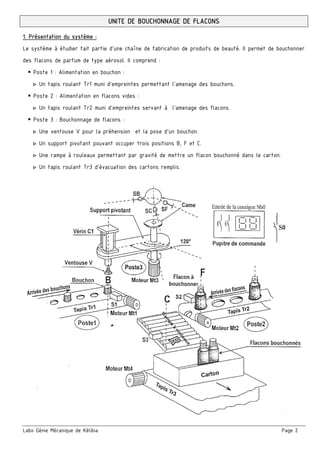
Moteur
Engrenage conique
(29 - 31)
r1 = 1 ; η1=0,95
Arbre (8)
N8=1400 tr/min
P8= 0,6 kW
Engrenage
(24 – 17a)
r2 =2 ; η2=0,85
Engrenage
(17b – 5)
r3 = 3/4 ; η3=0,85
Moteur 1 Moteur 2 Moteur 3
Nm [tr/min] 800 900 1000
Cm [N.m] 8 9 10](https://image.slidesharecdn.com/42017-2018-171002194618/85/Cahier-Meca-4ST-28-320.jpg)


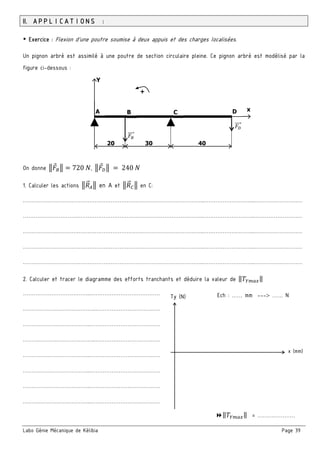
![Labo Génie Mécanique de Kélibia Page 40
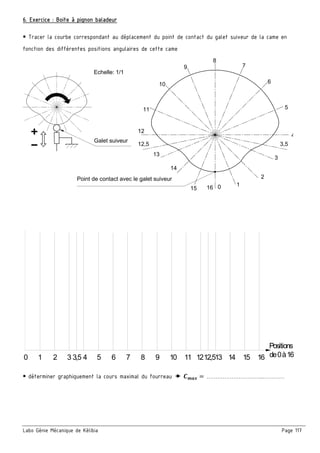
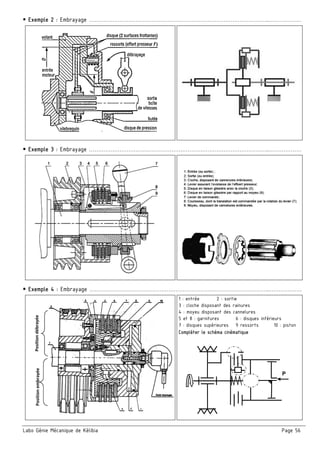
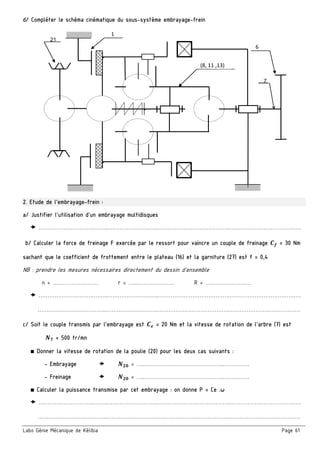
3. Calculer et tracer le diagramme des moments fléchissant et déduire la valeur de ‖ ‖
…………………………………..………………………………
………………………………..…………………………………
…………………………………..………………………………
………………………………..…………………………………
………………………………..…………………………………
………………………………..…………………………………
………………………………..…………………………………
………………………………..…………………………………
………………………………..…………………………………
………………………………..…………………………………
………………………………..…………………………………
………………………………..…………………………………
………………………………..…………………………………
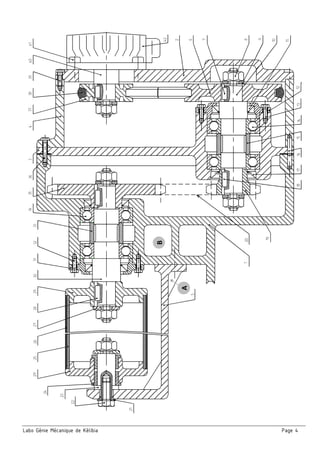
4. L’arbre est réalisé d’un acier C22 et de diamètre 18 ,
en adoptant un coefficient de sécurité 5
a. Calculer la valeur de la contrainte tangentielle moyenne
………………………………………………………………………………………..………………………..………………………
………………………………………………………………………………………..………………………..………………………
………………………………………………………………………………………..………………………..………………………
b. Calculer la valeur de la contrainte normale dans la section la plus sollicitée de la poutre
………………………………………………………………………………………..………………………..………………………
………………………………………………………………………………………..………………………..………………………
………………………………………………………………………………………..………………………..………………………
………………………………………………………………………………………..………………………..………………………
………………………………………………………………………………………..………………………..………………………
Materiau S185 E335 C22 C25
Re [MPa] 185 335 225 285
MFz (Nm)
x (mm)
‖ ‖ = …………………
Ech : …… mm --- …… Nm](https://image.slidesharecdn.com/42017-2018-171002194618/85/Cahier-Meca-4ST-45-320.jpg)



![Labo Génie Mécanique de Kélibia Page 44
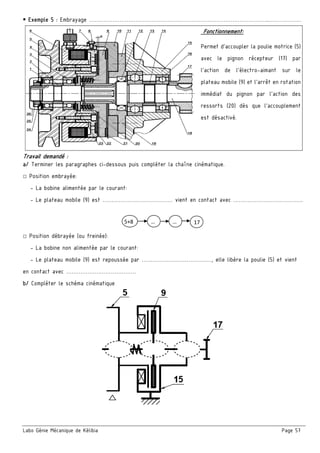
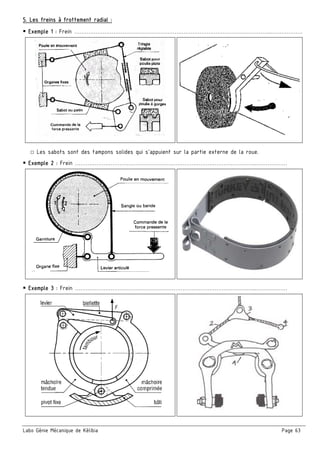
■ Exercice : Flexion d’une planche de plonger (piscine).
Une vis sans fin, assimilée à une poutre encastrée en A en cas de freinage, de section circulaire pleine
constante de diamètre d et de longueur L= 80 mm, encastré d’un côté et supportant trois charges localisées
en B et C et D
On donne 500 , 3000
1. Etudier l’équilibre de la planche et déterminer les actions mécaniques de l’encastrement et :
…………………………………………….……………………………………………..………………………..……………………
…………………………………………………..………………………………………..………….…..…………………..…………
………………………………………………..………………………………………..……………..…………………..………….…
…………………………………………………..………………………………………..………….…..…………………..…………
2. Calculer et tracer le diagramme des moments fléchissant et déduire la valeur de ‖ ‖
Zone [AB] …………………………………......………………
………………………………..…………………………………
Zone [AB] ……………………..………………………………
………………………………..…………………………………
……………………………..……………………………………
Zone [AB] …………………..……………….………………
………………………………..…………………………………
……………………………..……………………………………
b. Calculer la valeur de la contrainte normale dans la section la plus sollicitée de la poutre
………………………………………………………………………………………..………………………..………………………
………………………………………………………………………………………..………………………..………………………
Y
+
A D x
25 25 30
CB
MFz (Nm)
x (mm)
‖ ‖ = …………………
Ech : …… mm --- …… Nm](https://image.slidesharecdn.com/42017-2018-171002194618/85/Cahier-Meca-4ST-49-320.jpg)




































![Labo Génie Mécanique de Kélibia Page 111
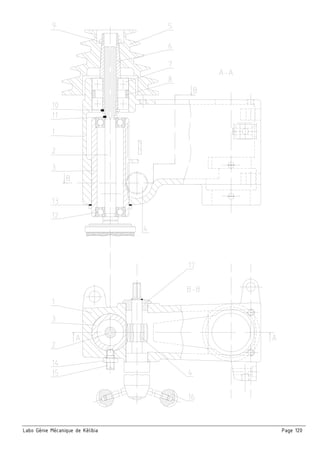
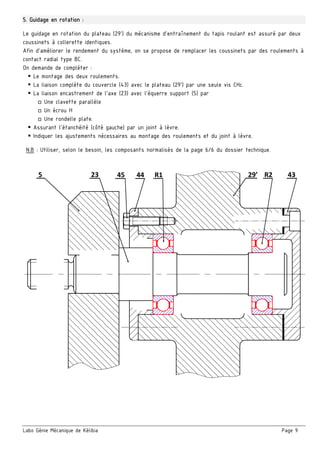
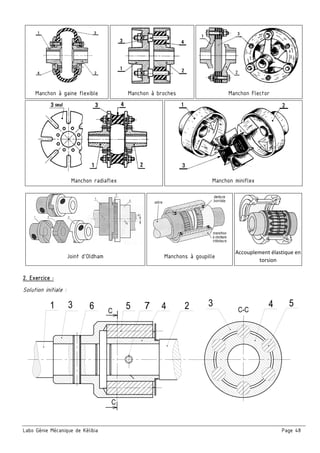
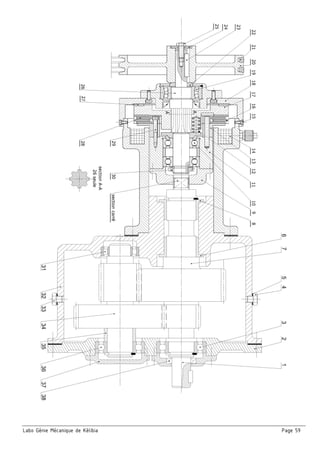
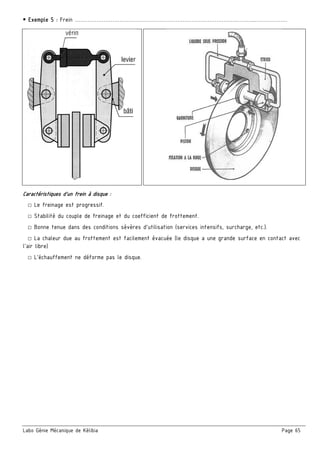
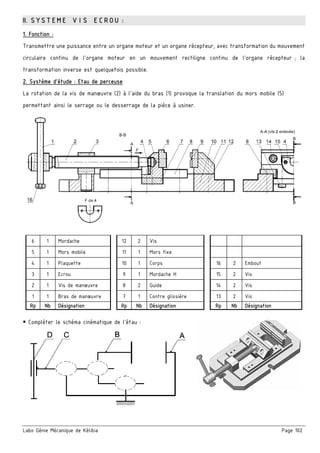
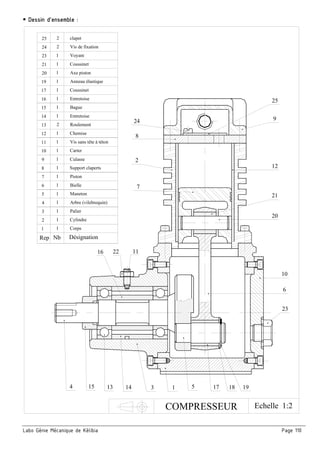
Schéma cinématique du compresseur :
□ On donne un schéma spatial et un schéma cinématique en vue de face et son ébauche suivant la vue de
gauche. On demande de terminer le schéma en vue de gauche et indiquer les repères des pièces
Caractéristiques du compresseur :
□ Mesurer sur le dessin d’ensemble (à l’échelle 1/2 ) le rayon de la manivelle
(R = L’excentricité (e) entre l’axe de rotation du vilebrequin (4) et l’axe du
maneton (5))
R mesuré = ……………………
□ Exprimer la course du piston (C) en fonction de (R) et donner sa valeur.
C = ……………………………………………………………………………
………………………………….……………..…………..…………….....
□ Calculer la cylindrée du compresseur en cm3
∅ Alésage = ∅ piston = d = ……..…… cm
Surface de l’alésage S = ………..……………………………………
Course (C) = ……..…… cm
Cylindrée du compresseur : V = S x C x n = ……………………………….……………= ………………cm3
□ Vérifier la valeur du débit volumique du compresseur :
Cylindrée = …………… cm3
;
Vitesse de rotation = 1500 tr/min (voir spécification CDCF)
Débit volumique (Qv) en cm3
/min = ………..………………………………………………………………..….………
(Qv) en l/min (ou dm3
/min) = ………..………………………………………………………………………..….………
Cylindrée d’un compresseur :
La cylindrée d’un compresseur est le volume (V) déplacé pour un tour de vilebrequin.
Cylindrée = [Surface de l’alésage (S) x Course du piston (C)] x nombre de cylindres (n)
é
.
4
Débit volumique d’un compresseur :
Le débit volumique (Qv) d’un compresseur est le volume déplacé pendant une minute
Qv = Cylindrée (cm3) x Vitesse de rotation (trs/min)
…
……
…
A-A
X
Z
O
A
B
C
Z
YO
A
B
C
e](https://image.slidesharecdn.com/42017-2018-171002194618/85/Cahier-Meca-4ST-116-320.jpg)