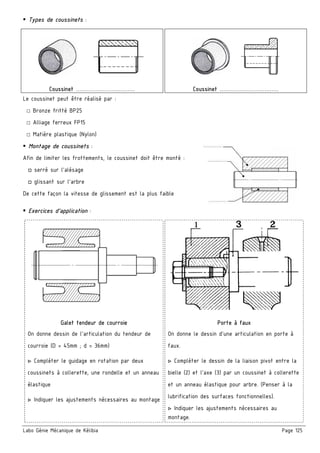
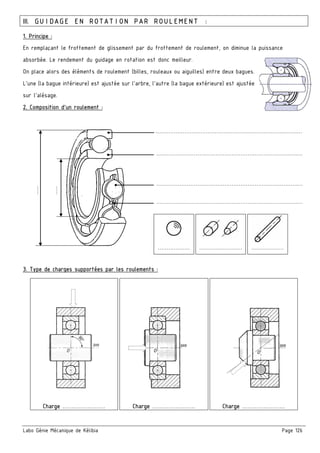
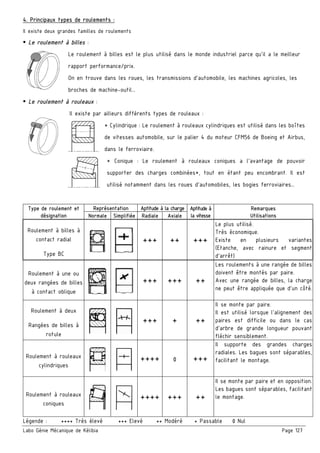
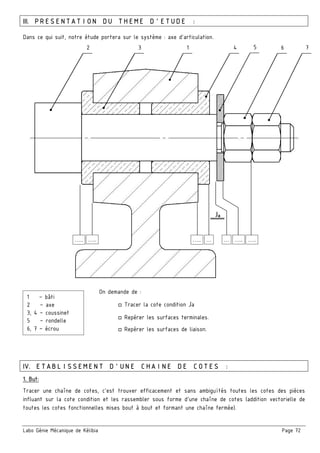
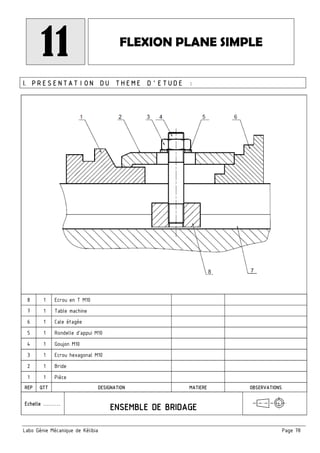
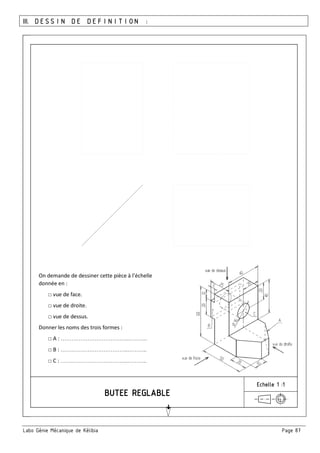
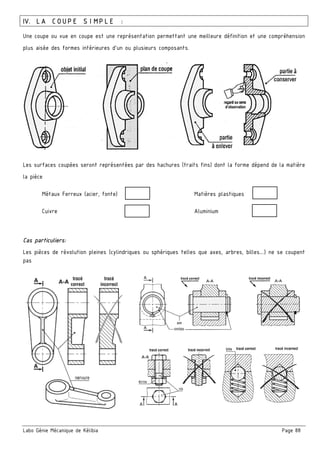
Le document traite des tolérances géométriques et de la cotation fonctionnelle dans le contexte de la mécanique, en détaillant les types de tolérances (forme, orientation, position) et leur application au sein d'assemblages mécaniques. Il aborde également la chaîne de cotes, son établissement, et les règles à respecter pour garantir un bon fonctionnement des mécanismes. En outre, le texte inclut des exercices d'application pour illustrer la théorie discutée.































![Labo Génie Mécanique de Kélibia Page 121
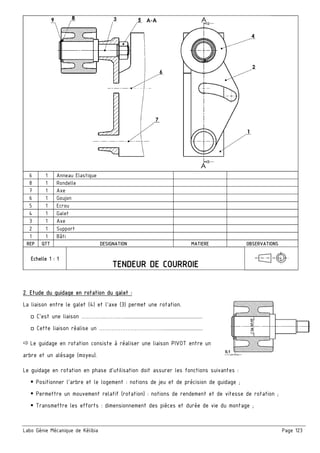
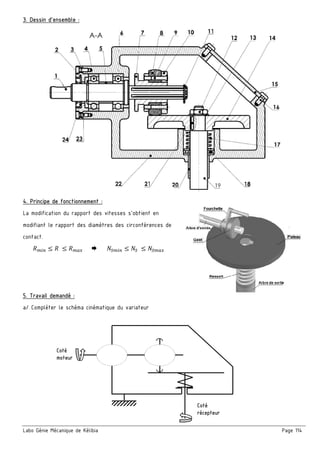
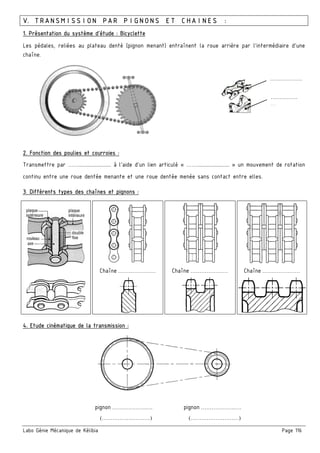
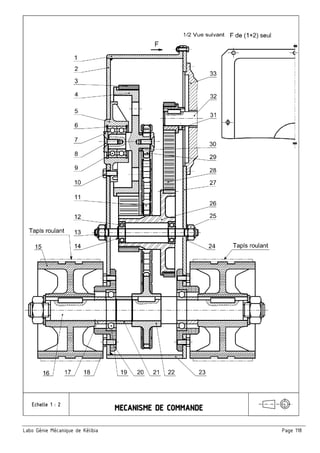
a/ Etude cinématique de la transmission [1] par poulies / courroie (31 – 26a)
a.1/ Quel est le type de la courroie (28)
……………..………………………..………………………………….………………………………….
a.2/ Calculer le rapport de transmission r1
……………..………………………..………………………………….………………………………….
b/ Etude cinématique de la transmission [2] par poulies / courroie (26b - 4)
b.1/ Calculer le diamètre de la poulie (4) sachant que le rapport de transmission r2 = 1/4
……………..………………………..………………………………….………………………………….
c/ Etude cinématique de la transmission [3] par pignonss / chaîne (29 - 22)
c.1/ Quel est le type de la chaîne (11)
…………..…………..……………..………………………………….………………………………….
c.2/ Calculer le rapport de transmission r3 sachant que le rapport global de la transmission est rg = 1/12
……………..………………………..………………………………….………………………………….
c.3/ En déduire le nombre de dents Z29 du pignon (29)
……………..………………………..………………………………….………………………………….
d/ Calculer la vitesse de rotation du moteur Nm
…………..…………..……………..………………………………….………………………………….
e/ Calculer le rapport global de la transmission ηg
…………..…………..……………..………………………………….………………………………….
f/ En déduire la puissance du moteur Pm
…………..…………..……………..………………………………….………………………………….
…………..…………..……………..………………………………….………………………………….
g/ Calculer la vitesse de translation du tapis roulant V15 sachant que R15 = 60mm
…………..…………..……………..………………………………….………………………………….
…………..…………..……………..………………………………….………………………………….
…………..…………..……………..………………………………….………………………………….
…………..…………..……………..………………………………….………………………………….](https://image.slidesharecdn.com/cahiertroisiemepartie2mtaallahmohamed-200116112854/85/Cahier-Meca-3-ST-Part-2-2-53-320.jpg)