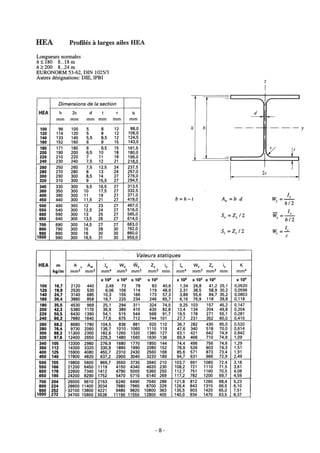
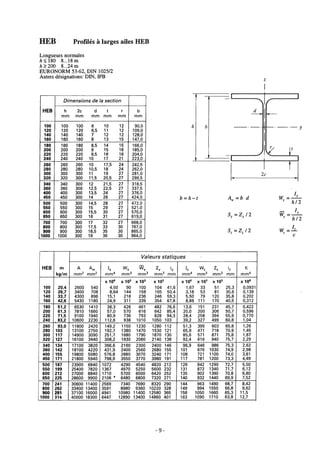
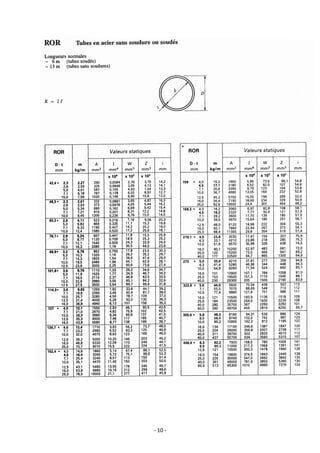
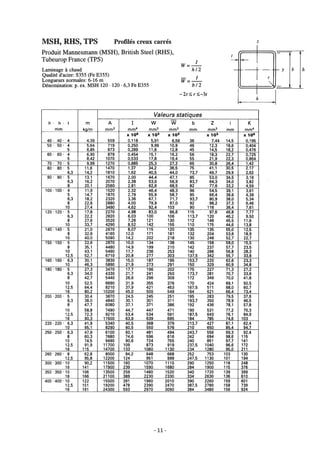
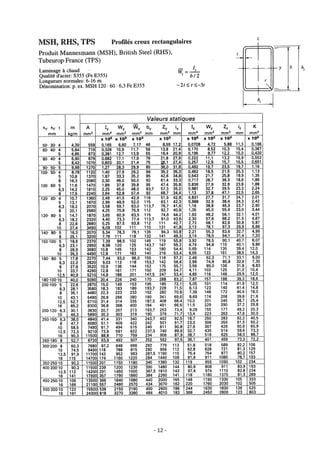
Le document fournit une série d'exercices et de solutions liés à l'analyse des structures, tirés de plusieurs ouvrages de référence. Il couvre des thématiques comme l'équilibre des forces, les éléments des structures, et inclut diverses hypothèses sur le comportement des matériaux. Une table des matières détaillée est également incluse, décomposant les exercices par chapitre et fournissant des instructions sur la résolution des problèmes présentés.

















































![- 64 -
Chapitre 1 Solutions - Compositions de forces.
1.1 R=8,026 kN à 88,77° de l’horizontal.
1.2 500N dans le fil incliné & 300N dans le fil horizontal.
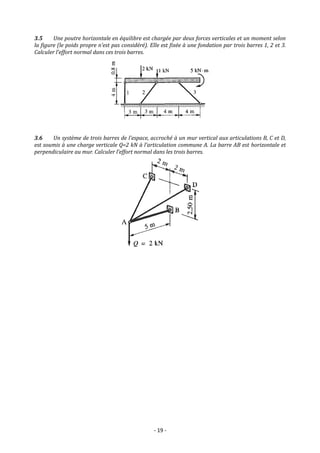
1.3 (a) Si α=0, 𝑀𝐵=188 Nm ; (b) 𝑀𝑚𝑎𝑥=200 Nm quand F est ⊥ à AB ; (c) Si α =20°, F=261 N.
1.4 𝐹𝑥 = 24,603 ; 𝐹𝑦 = 36,905 𝑘𝑁 ; 𝐹𝑧 = −246,034 𝑘𝑁
1.5 𝑀𝑥 = −3690,5 𝑘𝑁𝑚 ; 𝑀𝑦 = 492,1 𝑘𝑁𝑚 ; 𝑀𝑧 = −295,2 𝑘𝑁𝑚
Chapitre 2 Solutions - Equilibres
2.1 𝐹𝑅 = 78,5 𝑁 ; 𝑀𝑅 = 172, 4 𝑁𝑚.
2.2 Le poids, de 625 kN, agit à 10,88m du bord vertical gauche.
2.3 𝐹𝑅𝑋 = 193,55 𝑘𝑁 (←) ; 𝐹𝑅𝑌 = 1113,55 (↓) ; 𝑥𝑅 = 1,68 𝑚.
2.4 𝐹𝑅𝑋 = 2 𝑘𝑁 ; 𝐹𝑅𝑌 = 0 ; 𝑀𝑂𝑋 = 0 ; 𝑀𝑂𝑌 = 4,8 𝑘𝑁𝑚 ; 𝑀𝑂𝑍 = −3 𝑘𝑁𝑚.
2.5 𝐶 = 24,5 𝑘𝑁 (↗) ; 𝐷 = 22,7 𝑘𝑁(→)
2.6 L’équilibre en translation ∑ 𝐹𝑋 𝑒𝑡 ∑ 𝐹𝑌 = 0 est vérifié. L’équilibre en rotation
∑ 𝑀 = 48𝑘𝑁𝑚 ≠ 0 n’est pas vérifié ; il subsiste un moment résultant 𝑀𝑅.
2.7 Equilibre du bloc :
∑ 𝐹𝑣 = 0 → 𝑅 = 0,3𝐹𝑐1 + 5
∑ 𝐹ℎ = 0 → 𝐹𝑐1 = 0,6 𝑅 → 𝐹𝑐1 = 0,6 [0,3 𝐹𝑐1 + 5] = 𝟑, 𝟔𝟓𝟖 𝒌𝑵
→ 𝑅 = 0,3 . 3,658 + 5 = 𝟔, 𝟎𝟗𝟕 𝒌𝑵
Equilibre du coin :
∑ 𝐹ℎ = 0 → 𝐹𝑐2 𝑐𝑜𝑠 5 = 𝐹𝑐1 + 0,3 𝐹𝑐2 𝑠𝑖𝑛 5 → 𝐹𝑐2 = 3,77 𝑘𝑁
∑ 𝐹𝑣 = 0 → 𝐹𝑐2 𝑠𝑖𝑛 5 + 0,3 𝐹𝑐2 𝑐𝑜𝑠 5 + 0,3 𝐹𝑐1 = 𝑃
→ 𝑃 = 3,77 𝑠𝑖𝑛 5 + 0,3 . 3,77 𝑐𝑜𝑠 5 + 0,3 . 3,658 = 𝟐, 𝟓𝟓 𝒌𝑵
𝑷𝒎𝒊𝒏 = 𝟐𝟓𝟓𝟎 [N]](https://image.slidesharecdn.com/exercicesmds1-220809160754-b40eaa67/85/Mecanique-des-structures-et-RDM-Exercices-corriges-64-320.jpg)


![- 67 -
6.3 (a) Représentation des forces dues à la présence de l’eau :
(b) Calcul des réactions d’appuis :
∑ 𝐹𝑣 =
𝑁𝐵𝐷
√2
+ 𝑉𝐴 − 40 −
10
2
= 0
∑ 𝐹ℎ =
𝑁𝐵𝐷
√2
−
10
2
+ 𝐻𝐴 +
10
2
= 0 →
𝑁𝐵𝐷
√2
= −𝐻𝐴
∑ 𝑀𝐴 =
𝑁𝐵𝐷
√2
. 4 − 40 . 2 −
10
2
. 0,33 −
10
2
. 4,33 +
10
2
. 0,33 = 0
→
𝑁𝐵𝐷
√2
=
80+21,66
4
= 25,42 𝑘𝑁 = −𝐻𝐴
∑ 𝐹𝑣 = 0 → 𝑉𝐴 = −
𝑁𝐵𝐷
√2
+ 40 + 5 = 19,58 kN
HA = -25,42 kN VA = 19,58 kN 𝑵𝑩𝑫 = 35,95 kN ( Compression )
6.4 (a) Calcul du poids de la caisse :
Equilibre du point D :
Tension dans la corde qui passe par la poulie = 5 kN
Poids minimum de la caisse : 𝑩𝒎𝒊𝒏 = 10 [kN] (𝑭𝒔 = 𝟐)
(b) Calcul des réactions d’appuis :
Equilibre du point D : 𝐻𝐸 = −3 𝑘𝑁
Tension dans le sens du cable : 𝑉𝐸 = 0𝑘𝑁 et 𝑀𝐸 = 0𝑘𝑁
𝑀𝐴 = -2,50 . 3,5 = -8,75 kNm
𝑉𝐴 = P = 2,50 kN
𝑉𝐴 = 0
VA = 2,5 [kN] ; HA = 0 [kN] ; MA = -8,75 [kNm] ; VE = 0 [kN] ; HE = -3 [kN] ; ME = 0 [kNm]
6.5 Calcul de la force exercée sur la canette :
∑ 𝐹𝑉 en D : Force sur la canette = 𝑅 𝑐𝑜𝑠 𝛼.
L’équilibre de la partie supérieure de la structure donne ∑ 𝑀𝐴 = 0
𝑅 𝑐𝑜𝑠 𝛼 . 4 = 𝑃 . 20
𝐹 = 𝑅 𝑐𝑜𝑠 𝛼 = 𝑃 . 5 = 𝟓𝟎𝟎 𝑵
3 kN
F = 4 kN
√3² + 4² =
5 kN
α](https://image.slidesharecdn.com/exercicesmds1-220809160754-b40eaa67/85/Mecanique-des-structures-et-RDM-Exercices-corriges-67-320.jpg)
![- 68 -
6.6 Décomposition de la force F :
𝐹 𝑠𝑖𝑛
𝛼
2
= 𝜇 𝐹 𝑐𝑜𝑠
𝛼
2
𝑇𝑔
𝛼
2
= 0,25
𝛼
2
= 14,03
𝜶 = 𝟐𝟖 °
6.7 Pour le calcul, on considère une tranche de 1m de structure.
(a) Calcul de la sécurité au glissement :
La charge q vaut : 𝑞 = 𝛾 . 3 = 60 𝑘𝑁/𝑚².
𝐹𝑠 =
𝐹𝑠𝑡𝑎𝑏
𝐹𝑑é𝑠𝑡𝑎𝑏
=
𝑞 . 𝑥 . 𝜇
𝑝𝑚𝑎𝑥 . 𝐻
2
= 1,5
𝑥 =
1,5 .30
60 .0,6
= 1,25 𝑚
𝒙𝒎𝒊𝒏 = 𝟏, 𝟐𝟓 [𝒎]
(b) Calcul de la sécurité au renversement :
𝐹𝑠 𝑟𝑜𝑡 =
𝑀𝑠𝑡𝑎𝑏
𝑀𝑑é𝑠𝑡𝑎𝑏
=
𝑞 . 𝑥 .(
𝑥
2
+𝑦)
𝑃 . 𝐻/3
= 2
75
𝑥
2
+ 75 𝑦 = 30 . 1 . 2
𝑦 =
16,125
75
𝑦 = 0,175 𝑚
𝒚𝒎𝒊𝒏 = 𝟎, 𝟏𝟖 [𝒎]
Chapitre 7 Solutions - Treillis
7.1 Degré d’hyperstaticité : I=b+r-2n=12+3-2.8=-1 (c’est un mécanisme).
7.2 𝑁1 = −160 𝑘𝑁 (𝑐𝑜𝑚𝑝); 𝑁2 = −56,6 𝑘𝑁 (𝑐𝑜𝑚𝑝); 𝑁3 = 20 𝑘𝑁 (𝑡𝑟𝑎𝑐𝑡)
7.3 𝑁1 = 45 𝑘𝑁 (𝑡𝑟𝑎𝑐𝑡); 𝑁2 = 16,77 𝑘𝑁 (𝑡𝑟𝑎𝑐𝑡); 𝑁3 = −37,5 𝑘𝑁 (𝑐𝑜𝑚𝑝)
7.4 𝑁1 = 𝑁2 = 𝑁3 = 𝑁10 = 0 ; 𝑁4 = 8 𝑘𝑁 (𝑡𝑟𝑎𝑐𝑡) ; 𝑁5 = −8,49 𝑘𝑁(𝑐𝑜𝑚𝑝) ; 𝑁6 = −4 𝑘𝑁 (𝑐𝑜𝑚𝑝)
𝑁7 = 2,83 𝑘𝑁 (𝑡𝑟𝑎𝑐𝑡) ; 𝑁8 = −8 𝑘𝑁 (𝑐𝑜𝑚𝑝) ; 𝑁9 = 11,31 𝑘𝑁 (𝑡𝑟𝑎𝑐𝑡)
7.5 𝑁1−3 = 𝑁5−6 = 0 ; 𝑁1−2 = −80 𝑘𝑁 (𝑐𝑜𝑚𝑝) ; 𝑁3−4 = −60 𝑘𝑁 (𝑐𝑜𝑚𝑝) ;
𝑁4−6 = −75 𝑘𝑁 (𝑐𝑜𝑚𝑝) ; 𝑁2−3 = 90,14 𝑘𝑁 (𝑡𝑟𝑎𝑐𝑡) ; 𝑁3−6 = 18,03 𝑘𝑁 (𝑡𝑟𝑎𝑐𝑡).
𝐹 cos
𝛼
2
𝐹 sin
𝛼
2
α](https://image.slidesharecdn.com/exercicesmds1-220809160754-b40eaa67/85/Mecanique-des-structures-et-RDM-Exercices-corriges-68-320.jpg)

![- 71 -
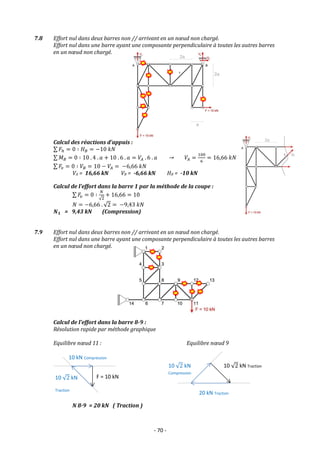
7.10 Effort nul dans deux barres non // arrivant en un nœud non chargé.
Effort nul dans une barre ayant une composante perpendiculaire à toutes les autres barres
en un nœud non chargé.
Calcul des réactions d’appuis :
∑ 𝐹ℎ = 0 ∶ 𝐻𝐴 = −10 𝑘𝑁
∑ 𝑀𝐴 = 0 ∶ 10 . 3 . 𝑎 − 10 . 𝑎 = 𝑉𝐵 . 6 . 𝑎 → 𝑉𝐵 =
20
6
= 3,33 𝑘𝑁
∑ 𝐹𝑣 = 0 ∶ 𝑉𝐴 = 10 − 𝑉𝐵 = 6,66 𝑘𝑁
VA = 6,66 [kN] HA = -10 [kN] VB = 3,33 [kN]
Calcul de l’effort dans la barre 1 :
Par la méthode de la coupe :
∑ 𝑀𝐶 = 0 ∶ 𝑁 . 𝑎 − 10 . 𝑎 + 𝑉𝐵 . 3𝑎 = 0
→ 𝑁 = 10 − 3,333 . 3 = 0 𝑘𝑁
𝑵𝟏 = 0 [kN]
7.11
Calcul des réactions d’appuis suivantes :
∑ 𝐹𝑉 = 0 ∶ 𝑉𝐴 + 𝑉𝐵 = 20 𝑘𝑁
∑ 𝐹𝐻 = 0 ∶ 𝐻𝐴 = −10 𝑘𝑁
∑ 𝑀𝐴 = 0 ∶ 10 𝑎 + 10 𝑎 + 10 . 3𝑎 = 𝑉𝐵 . 10
𝑉𝐴 = 7,5 [kN] 𝑉𝐵 = 12,5 [kN] 𝐻𝐴 = -10 [kN]
Calcul des efforts internes :
On peut rapidement calculer les efforts dans l’ensemble des barres en utilisant la méthode
graphique.
𝑵𝟏 = 10,61 [kN] c 𝑵𝟐 = 17,5 [kN] t 𝑵𝟑 = 5 [kN] c 𝑵𝟒 = 3,54 [kN] c
𝑵𝟓 = 3,54 [kN] t 𝑵𝟔 = 12,5 [kN] t 𝑵𝟕 = 10 [kN] t 𝑵𝟖 = 17,68 [kN] c](https://image.slidesharecdn.com/exercicesmds1-220809160754-b40eaa67/85/Mecanique-des-structures-et-RDM-Exercices-corriges-71-320.jpg)
![- 72 -
7.12 Calcul des réactions d’appuis :
∑ 𝐹ℎ = 0 → 𝐻𝐴 = −10
∑ 𝐹𝑣 = 0 → 𝑉𝐴 + 𝑉𝐵 = 10
∑ 𝑀𝐴 = 0 → 10 . 𝑎 + 7𝑎 . 𝑉𝐵 = 3𝑎 . 10 → 𝑉𝐵 = 20/7
→ 𝑉𝐴 = 50/7
VA = 7,14 [kN] HA = -10 [kN] VB = 2,86 [kN]
Calcul de l’effort dans la barre 1 :
Méthode graphique au nœud inférieur gauche :
Equilibre nœud 11 :
Equilibre à l’appui A :
∑ 𝐹ℎ = 0 → 𝐻𝐴 + 10 − 𝑥 𝑐𝑜𝑠 45 = 0 → −10 + 10 − 𝑥 𝑐𝑜𝑠 45 = 0
→ 𝑥 𝑐𝑜𝑠 45 = 0 → 𝒙 = 𝟎
𝑵𝟏 = 0 [kN]
10 kN
Compression
F = 10 kN
10 √2 kN
Traction](https://image.slidesharecdn.com/exercicesmds1-220809160754-b40eaa67/85/Mecanique-des-structures-et-RDM-Exercices-corriges-72-320.jpg)
![- 73 -
Chapitre 8 Solutions - Arcs funiculaires & câbles
8.1 Calcul des réactions d'appui :
Le calcul des réactions d'appui verticales est immédiat grâce à la symétrie. La réaction
horizontale s'obtient par équilibre des couples sur le demi tronçon gauche par rapport à la
clé de l'arc (située forcément à mi-portée grâce à la symétrie) :
H
qL
R
L
L
q
L
L
q
H
R
L
R
qL
L
q
L
q
R
R
H
H
VA
VB
VA
32
7
8
4
2
8
3
4
2
4
3
2
2
4
2
2
1
2
Calcul de la géométrie de l'arc sur le tronçon AC :
Sur le tronçon AC, le moment fléchissant M(x,y) vaut :
2
32
7
4
3
,
2
2
qx
y
H
qL
x
qL
y
x
M
M(x,y) devant être nul quels que soient x et y, on trouve :
0
M
2
4
3
²
7
32 2
x
Lx
L
H
y
Cette équation est l'équation de la fibre moyenne de l'arc sur le tronçon AC, telle que le
moment fléchissant y est partout nul.
Calcul de la géométrie de l'arc sur le tronçon CD :
Sur le tronçon CD, M(x,y) vaut :
2
)
4
/
(
2
)
8
/
(
4
32
7
4
3
,
2
2
L
x
q
L
x
qL
y
H
qL
x
qL
y
x
M
M devant être nul quels que soient x et y, on trouve :
0
M
32
7
32 2
2
2
L
x
Lx
L
H
y
Dimensionnement de la section nécessaire :
𝐹𝑚𝑎𝑥 = 43,41 𝑘𝑁 ; section circulaire R= 1cm
Géométrie finale de l'arc :
On voit sur la figure ci-dessous qu'une discontinuité dans la répartition des charges
distribuées n'implique aucune discontinuité dans la géométrie de l'arc. En effet, si on calcule
la valeur des dérivées des deux fonctions correspondant respectivement aux tronçons AC et
CD en x = L/4, on trouve une même valeur 16H/7L, ce qui prouve que les deux courbes y
sont tangentes. Remarquons que l'on aurait pu trouver le même résultat en utilisant le
théorème d'analogie avec la poutre.
0
1
2
3
4
0 1 2 3 4 5 6 7 8 9 10
Equation valable pour x > L /4
Jonction en L /4 Jonction en 3L /4
Géométrie finale
Equation valable pour x < L /4
L = 10 [m], h = 3 [m]
C
7qL2
/32H
3qL/4
x
y M(x,y) = 0
q [kN/m]
2q [kN/m]
A
7qL2
/32H
3qL/4
x
y
M(x,y) = 0
q [kN/m]
A
L=10 m, H=3m](https://image.slidesharecdn.com/exercicesmds1-220809160754-b40eaa67/85/Mecanique-des-structures-et-RDM-Exercices-corriges-73-320.jpg)
![- 74 -
8.2 Calcul des réactions d'appui :
Le calcul des réactions d'appui verticales est immédiat grâce à la symétrie. La réaction
horizontale s'obtient par équilibre des couples sur le demi tronçon gauche par rapport à la
clé de l'arc :
H
QL
R
L
Q
H
R
L
R
Q
R
R
H
H
VA
VB
VA
4
4
2
Calcul de la géométrie de l'arc sur le tronçon AC :
Sur le tronçon AC, on a : y
H
QL
Qx
y
x
M
4
,
M devant être nul quels que soient x et y, on trouve : x
L
H
y
M
4
0
Cette équation est donc l'équation de la fibre moyenne de l'arc sur le tronçon AC, telle que le
moment fléchissant y est nul partout. Cette équation est celle d'une droite. Le tronçon AC est
donc rectiligne.
Calcul de la géométrie de l'arc sur le tronçon CD :
Sur le tronçon CD, on a : y
H
QL
Qx
L
x
Q
y
x
M
4
4
,
M devant être nul quels que soient x et y, on trouve :
H
y
M
0
Le tronçon CD est donc rectiligne et horizontal.
Géométrie finale de "l'arc"
Les calculs précédents montrent que la condition M = 0 transforme la structure en un portique
de hauteur H :
Remarquons que le même résultat serait obtenu en utilisant le théorème d'analogie avec la
poutre
Dimensionnement de la section nécessaire :
𝐹𝑚𝑎𝑥 = 22,36 𝑘𝑁 ; section carrée a= 4cm
QL/4H
Q
x
y
M(x,y) = 0
A
QL/4H
Q
x
y
M(x,y) = 0
A
Q [kN]
A B
H
L
C D
L/4 L/4
Q [kN]
Q [kN]](https://image.slidesharecdn.com/exercicesmds1-220809160754-b40eaa67/85/Mecanique-des-structures-et-RDM-Exercices-corriges-74-320.jpg)
![- 75 -
8.3 Comme pour l'exemple précédent, la dissymétrie des charges ne permet pas de savoir quelle
est l'abscisse du point haut de l'arc. Le théorème d'analogie avec le diagramme des moments
de la poutre (§7.5) permet toutefois de vérifier rapidement que la clé se situe sur le tronçon
CD, d'une part, et que ce dernier est horizontal, d'autre part. On propose cependant de
passer par une détermination analytique de l'équation de chaque tronçon.
Calcul des réactions d'appui :
Équilibre vertical : Q
qL
R
R VB
VA
2
Équilibre des moments par rapport à l'appui B :
4
4
3
2
L
Q
L
qL
L
RVA
Équilibre des moments à la clé (tronçon droit) : H
R
L
Q
L
R H
VB
4
2
On obtient :
2
qL
R
R VB
VA
et
H
qL
RH
8
2
Calcul de la géométrie sur le tronçon BD :
En tout point de coordonnées (x,y), le moment est nul et s'écrit :
0
8
2
)
,
(
2
y
H
qL
x
qL
y
x
M
On en déduit que le tronçon BD doit être rectiligne :
x
L
H
y
4
avec y(x=L/4) = H
Calcul de la géométrie sur le tronçon DC :
En tout point de coordonnées (x,y), le moment est nul et s'écrit :
0
4
/
2
8
2
)
,
(
2
L
x
qL
y
H
qL
x
qL
y
x
M
Et on en déduit que le tronçon BD doit être horizontal, ce qui confirme le calcul de la
géométrie du tronçon BD : H
y
Géométrie complète :
On sait que le funiculaire de la charge uniformément distribuée est une parabole qui s'arrête
dans ce cas à la clé de l'arc avec une tangente horizontale en C. Par ailleurs, les calculs
précédents ont montré que les deux autres tronçons doivent être rectilignes :
Pratiquement, cette structure pourrait être idéale dans les deux cas suivants.
Le premier concerne une passerelle ou un pont dont le tablier serait suspendu à la
structure :
Sur la partie droite, les suspentes convergent toutes vers le point haut et y exercent un effort
dont la résultante est verticale et égale à qL/2. Dans ce cas la partie droite du tablier reçoit
des efforts de compression qui proviennent des composantes horizontales des efforts de
traction dans les suspentes.
On peut aussi envisager le cas dual d'un tablier qui repose sur la structure par
qL2
/8H
qL/2
x
y
M(x,y) = 0
qL2
/8H
qL/2
x
y
M(x,y) = 0 Q = qL/2
A B
q [kN/m] Q = qL/2 [kN]
C D](https://image.slidesharecdn.com/exercicesmds1-220809160754-b40eaa67/85/Mecanique-des-structures-et-RDM-Exercices-corriges-75-320.jpg)



![- 82 -
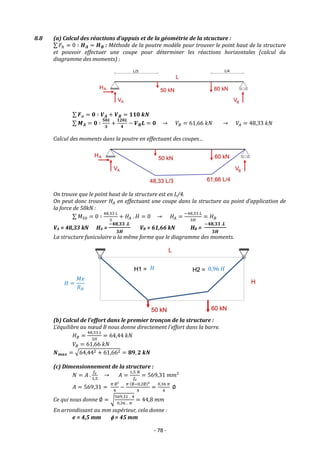
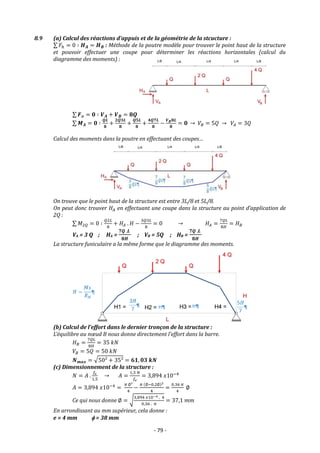
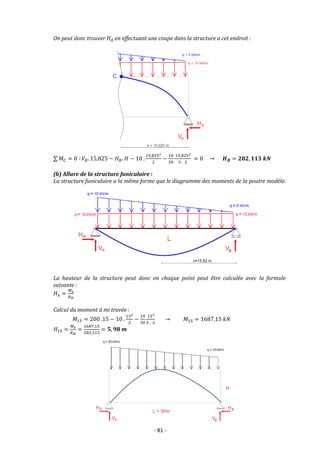
(c) Dimensionnement de la structure :
L’équilibre au nœud A nous donne directement l’effort maximal dans la structure.
𝐻𝐴 = 282,113 𝑘𝑁
𝑉𝐴 = 250 𝑘𝑁
𝑁𝑚𝑎𝑥 = √250² + 282,113² = 𝟑𝟕𝟔, 𝟗𝟒 𝒌𝑵
𝑁 = 𝐴 .
𝑓𝑒
𝛾
→ 𝐴 =
𝛾 . 𝑁
𝑓𝑒
= 3,14 𝑥10−4
𝑚𝑚2
𝐴 = 3,14 𝑥10−4
= 𝑏 . ℎ = 2𝑏²
Ce qui nous donne 𝑏 = √
3,14 𝑥10−4
2
= 125,32 𝑚𝑚
En arrondissant au mm supérieur, cela donne : 𝒉 = 𝟐𝟓, 𝟐 [𝒄𝒎] 𝒃 = 𝟏𝟐, 𝟔[𝒄𝒎]
Chapitre 9 Solutions - Efforts internes.
9.1 (a) NM dans 𝑆1 et VM dans 𝑆2 ; (b) NVM ; (c) NVM dans 𝑆2et N dans 𝑆3 ; (d) MN ; (e) MVN ;
(f) 𝑉
𝑧𝑇𝑀𝑦.
9.2 (a) V=-3kN, M= 12kNm (fibre sup. tendue) dans 𝑆𝑎 ; N=-3kN, M=6kNm (fibre gauche
tendue) dans 𝑆𝑏 ;
(b) N=-1,34 kN, V=-2,68 kN, M=9kNm (fibre sup. tendue) ;
(c) N=-4 kN, V= 1 kN, M=4kNm (fibre gauche tendue) ;
(d) V=-4 kN, M=8kNm (fibre sup. tendue).
9.3 𝑀𝐵 = 5,84 𝑘𝑁𝑚 (𝑓𝑖𝑏𝑟𝑒 𝑖𝑛𝑡. 𝑡𝑒𝑛𝑑𝑢𝑒); 𝑀𝐷 = 34,16 𝑘𝑁𝑚 (𝑓𝑖𝑏𝑟𝑒 𝑒𝑥𝑡. 𝑡𝑒𝑛𝑑𝑢𝑒).
9.4 À gauche de C : N=-76,3 kN, V=131,9 kN ; à droite de C : N=-24,9 kN, V=-132,1kN ;
𝑀𝐶 = 298,9 𝑘𝑁𝑚 (𝑓𝑖𝑏𝑟𝑒 𝑠𝑢𝑝. 𝑡𝑒𝑛𝑑𝑢𝑒).
9.5 N =-1 kN, 𝑉
𝑦 = 0,5 𝑘𝑁, 𝑉
𝑧 = −5,732 𝑘𝑁, 𝑇 = 4,5 𝑘𝑁𝑚, 𝑀𝑦 = 7,866 𝑘𝑁𝑚, 𝑀𝑧 = 1,25 𝑘𝑁𝑚.
9.6 (a) pour 0 ≤ 𝑥1 ≤ 𝐿 : N=0, V=
𝑞𝑎2
2𝐿
, M=
𝑞𝑎2𝑥1
2𝐿
; pour 0 ≤ 𝑥2 ≤ 𝑎 ∶ 𝑁 = 0, 𝑉 = −𝑞(𝑎 − 𝑥2),
𝑀 =
𝑞(𝑎−𝑥2)2
2
(fibre supérieure tendue)](https://image.slidesharecdn.com/exercicesmds1-220809160754-b40eaa67/85/Mecanique-des-structures-et-RDM-Exercices-corriges-82-320.jpg)
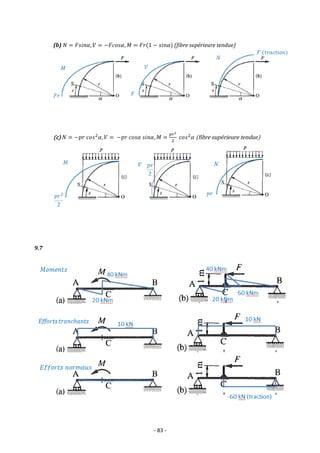
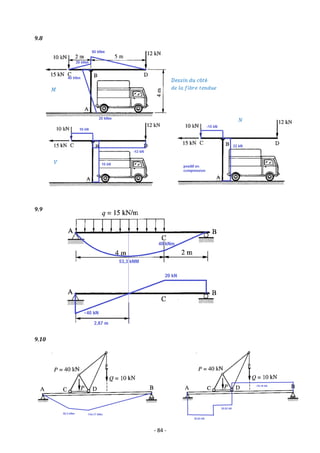
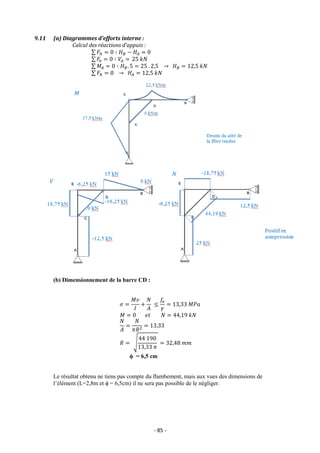
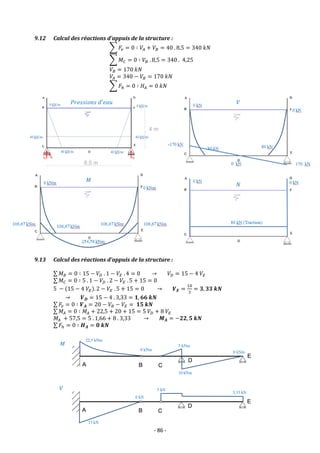
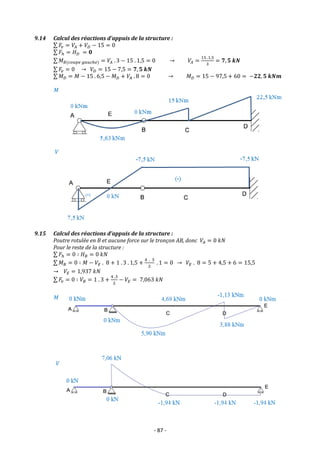
![- 88 -
9.16 (a) Réactions d’appuis :
Si on fait une coupe dans la rotule en B et qu’on fait l’équilibre de la partie gauche, on
trouve 𝑉𝐴 = 0.
Pour le reste de la structure :
∑ 𝐹𝑉 = 0 ∶ 𝑉𝐵 + 𝑉𝐸 = 2 . 8 + 5 + 7 + 3 . 8 .
1
2
∑ 𝐹𝐻 = 0 ∶ 𝐻𝐵 = 0
∑ 𝑀𝐵 = 0 ∶ 𝑉𝐸 . 8 = 7 . 6 + 5 . 3 + 2 . 8 . 4 + 3 . 8 .
1
2
.
8
3
𝑉𝐸 = 19,125 𝑘𝑁
∑ 𝐹𝑉 = 0 ∶ 𝑉𝐵 + 𝑉𝐸 = 40
𝑉𝐵 = 20,875 𝑘𝑁
VA = 0 [kN] VB = 20,875 [kN] HB = 0 [kN] VE = 19,125 [kN]
(b) Calcul du moment de flexion maximal dans la poutre :
On aura 𝑀𝑚𝑎𝑥 là où l’effort tranchant vaudra 0.
𝑉
𝑥 = 𝑉𝐸 − 2 . 𝑦 −
3
8
. 𝑦 .
𝑦
2
− 7 = 0
𝑦 = 4,316
𝑥 = 10 − 𝑦 = 5,68
On fait une coupe en x=3,68 m pour trouver la valeur du moment max.
𝑀𝑥 = 𝑉𝐸 . 𝑦 − 7 (𝑦 − 2) − 2 . 𝑦 .
𝑦
2
−
3
8
.
𝑦2
2
.
𝑦
3
(𝑎𝑣𝑒𝑐 𝑦 = 4,316)
𝑴𝒎𝒂𝒙 = 𝟒𝟐, 𝟔𝟖 [𝒌𝑵𝒎] à 𝑢𝑛𝑒 𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑒 𝒙 = 𝟓, 𝟔𝟖[𝒎] 𝑑𝑢 𝑝𝑜𝑖𝑛𝑡 𝐴.
(c) Diagramme des moments fléchissants :
(d) Diagramme des efforts tranchants :](https://image.slidesharecdn.com/exercicesmds1-220809160754-b40eaa67/85/Mecanique-des-structures-et-RDM-Exercices-corriges-88-320.jpg)
![- 89 -
9.17 (a) Calcul des réactions d’appuis :
Sachant que la poulie tourne sans frottement, la tension dans le câble ED vaut : 1,2 [kN]
(b) Efforts internes :](https://image.slidesharecdn.com/exercicesmds1-220809160754-b40eaa67/85/Mecanique-des-structures-et-RDM-Exercices-corriges-89-320.jpg)
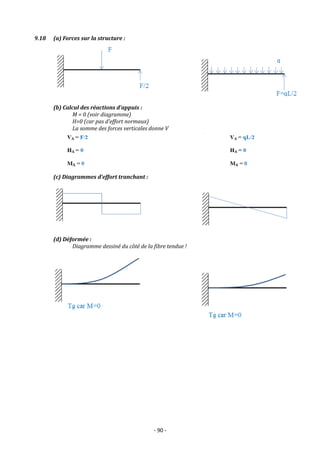
![- 91 -
9.19 (a) Calcul des réactions d’appuis :
Les réactions d’appuis verticales correspondent aux sauts dans le diagramme des efforts
tranchants.
𝑉𝐴 = 4,286 [kN] 𝑉𝐵 = 12,714 [kN] 𝐻𝐵 = 10 [kN]
(b) Calcul des charges :
Un saut dans le diagramme des efforts tranchants correspond à une charge ponctuelle.
Une variation linéaire du diagramme des efforts tranchants correspond à une charge répartie.
(c) Allure des moments fléchissant :
Le moment est maximal là ou l’effort tranchant vaut 0 (entre A et B ainsi que sur l’appui B).
Le moment est linéaire là ou l’effort tranchant est constant.
Le moment est non-linéaire là ou l’effort tranchant est linéaire.
Effort tranchant négatif, moments décroissant & effort tranchant positif, moment croissant.
Le diagramme des moments se dessine TOUJOURS du côté de la fibre tendue.
(d) Calcul du moment maximal :
Sur appui :
𝑀𝑚𝑎𝑥 = 10 . 1 . 0.5 = 𝟓 𝒌𝑵𝒎
En travée :
Le moment est max lorsque V=0. Avec Thales, V=0 en x = 2,643m
𝑀𝑚𝑎𝑥 = 𝑉𝐴. 𝑥 − 3 . (𝑥 − 1) − 2 .
(𝑥−2)2
2
= 𝟓, 𝟗𝟖 𝒌𝑵𝒎
𝑴𝒎𝒂𝒙 = 𝟓, 𝟗𝟖 [𝒌𝑵𝒎] à 𝑢𝑛𝑒 𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑒 𝒙 = 𝟐, 𝟔𝟒 [𝒎] 𝑑𝑢 𝑝𝑜𝑖𝑛𝑡 𝐴.](https://image.slidesharecdn.com/exercicesmds1-220809160754-b40eaa67/85/Mecanique-des-structures-et-RDM-Exercices-corriges-91-320.jpg)


![- 94 -
11.7 (a) Noyau central :
Comme la charge de compression Q est appliquée en dehors du
noyau central, in y aura de la traction quelque part dans la section.
(b) Calcul de la contrainte normale en B :
𝜎𝐵 = ±
𝑁
𝐴
±
𝑀𝑣
𝐼
±
𝑀𝑣
𝐼
=
𝑄
540
+
𝑄 .4 .15
40 500
+
𝑄 .2,5 .9
14 580
= 0,004876 𝑄 [
𝑁
𝑐𝑚2] 𝑠𝑖 𝑄 𝑒𝑠𝑡 𝑒𝑛 𝑁
(c) La contrainte de traction maximale se trouvera en D
(e) Calcul de 𝑸𝒎𝒂𝒙 :
𝜎𝐵 = 0,48 𝑄 ≤ 30 𝑀𝑃𝑎
𝑄𝑚𝑎𝑥 =
30
0,00004876
= 615 258 𝑁
11.8 (a) Noyau central de la structure nécessaire pour éviter l’apparition de contraintes de traction
dans la section.
Noyau central circulaire de rayon « a ».
(b) Epaisseur minimale de la structure :
𝜎 =
𝑀𝑦
𝐼
−
𝑁
𝐴
=
𝑃.𝑎 .𝑅
𝜋𝑅4
4
−
𝜋𝑟4
4
−
𝑃
𝜋𝑅2−𝜋𝑟2 = 0
𝑎 =
𝑅4−𝑟4
4𝑅(𝑅2−𝑟2)
=
(𝑅2−𝑟2)(𝑅2+𝑟2)
4𝑅(𝑅2−𝑟2)
=
𝑅2+𝑟2
4𝑅
𝑎 = 0,51 & 𝑟 = 1𝑚
On résout l’équation en R² et on trouve :
𝑅 = 1,22 𝑚
𝑒 = 𝑅 − 𝑟 = 𝟎, 𝟐𝟐 𝒎](https://image.slidesharecdn.com/exercicesmds1-220809160754-b40eaa67/85/Mecanique-des-structures-et-RDM-Exercices-corriges-94-320.jpg)

![- 96 -
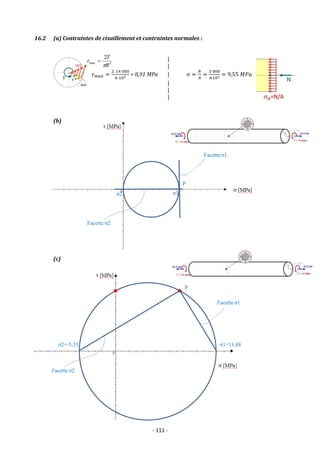
Chapitre 12 Solutions - Effort tranchant
12.1 𝜏𝑚𝑎𝑥 =
3𝑉
2𝑏ℎ
= 7,77 𝑀𝑃𝑎
12.2 Matériau fragile : 𝜏𝑐𝑟𝑖𝑡 =
𝑓𝑒
𝛾
→ L/h = 0.25
Matériau ductile ; 𝜏𝑐𝑟𝑖𝑡 =
𝑓𝑒
√3 𝛾
→ L/h = 0.43
12.3 (a) contraintes de cisaillement :
Si les deux poutres ne sont PAS solidaires. | Si les deux poutres sont solidaires.
|
|
|
|
|
|
max= 0,3 [MPa] | max = 0,3 [MPa]
(b) Contraintes normales :
|
|
|
|
|
|
max = 48 [MPa] | max= 24 [MPa]
(c) Dimensionnement du nombre de clous :
Effort rasant à reprendre entre les deux poutres : 𝜏𝑚𝑎𝑥 . 𝑏 . 𝐿 = 0,3 . 100 . 2000 = 60 kN
Résistance d’un clou au cisaillement :
𝑓𝑒
𝛾 √3
𝐴 =
300
1,5 √3
28,27 = 3,26 𝑘𝑁
Il faut donc 19 clous au total.](https://image.slidesharecdn.com/exercicesmds1-220809160754-b40eaa67/85/Mecanique-des-structures-et-RDM-Exercices-corriges-96-320.jpg)

![- 98 -
(d) Dimensionnement pour le cas 1 :
Critère de Von Mises car l’acier est un matériau ductile :
𝜏𝑚𝑎𝑥 =
𝑇
2𝜋𝑅2𝑒
≤
𝑓𝑒
𝛾 .√3
= 90,45 𝑀𝑃𝑎
𝑅 = √
500 000
2 .𝜋 . 2 .90,45
= 20,97 𝑚𝑚
𝑹 = 𝟐, 𝟓 [cm] (arrondir au demi-centimètre)
(e) Contraintes de cisaillement pour le cas 2 :
𝜏𝑚𝑎𝑥 =
3𝑇
𝜋𝑅𝑒2
(f) Dimensionnement pour le cas 2 :
Critère de Von Mises car l’acier est un matériau ductile :
𝜏𝑚𝑎𝑥 =
3𝑇
𝜋𝑅𝑒2 ≤
𝑓𝑒
𝛾 .√3
= 90,45 𝑀𝑃𝑎
𝑅 =
3 .500 000
𝜋 .22 .90,45
= 1319,69 𝑚𝑚
𝑹 = 𝟏𝟑𝟐 [cm] (arrondir au demi-centimètre)
13.6 (a) Calcul des réactions d’appuis :
Rx = 0 Ry = 0 Rz =F Mx = 0 My = 4aF Mz = 0
(b) Allure des moments de torsion :
𝑻𝒎𝒂𝒙 = a F Unités : kNm
(c) Allure des contraintes de cisaillement dans la section la plus sollicitée :
𝜏𝑚𝑎𝑥 =
2𝑇
𝜋𝑅3
(d) Dimensionnement de la barre :
L’acier est ductile → Von Mises
𝑇𝑚𝑎𝑥 = 0,4 𝑘𝑁𝑚
𝜏𝑚𝑎𝑥 =
2 .0,4 𝑘𝑁𝑚
𝜋𝑅3 ≤
𝑓𝑒
𝛾√3
= 90,45 𝑀𝑃𝑎
𝑅³ . 𝜋 . 90,45 𝑀𝑃𝑎 = 2 . 0,4 𝑘𝑁𝑚
𝑅 = 0,014 𝑚 → On arrondi au demi cm supérieur : 𝑹 = 𝟏, 𝟓 [cm]](https://image.slidesharecdn.com/exercicesmds1-220809160754-b40eaa67/85/Mecanique-des-structures-et-RDM-Exercices-corriges-98-320.jpg)
![- 99 -
Chapitre 14 Solutions - Cercles de Mohr
14.1
14.2 Une contrainte de 10 kN/m² sur toutes surfaces d’orientation 𝛼 quelconque
→ Pression hydrostatique.
14.3 𝜏𝑚𝑎𝑥 = 2,5 𝑁/𝑚𝑚² ;
𝜎𝐼 = 0 𝑁/𝑚𝑚² (facette horizontale) ;
𝜎𝐼𝐼 = −5 𝑁/𝑚𝑚²(facette verticale)
14.4 𝜏𝑚𝑎𝑥 = 0,5 𝑀𝑃𝑎 ;
𝜎𝐼 = 4 𝑀𝑃𝑎 (facette horizontale) ;
𝜎𝐼𝐼 = 3 𝑀𝑃𝑎(facette verticale)
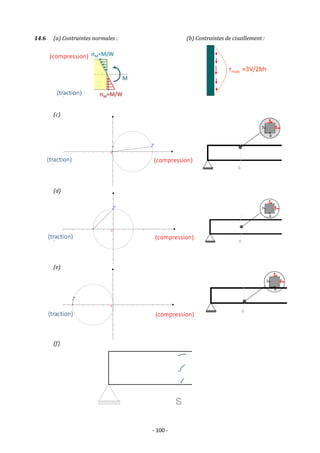
14.5 𝜏𝑚𝑎𝑥 = 12 𝑁/𝑚𝑚² ;
𝜎𝐼 = 18 𝑁/𝑚𝑚² (facette verticale) ;
𝜎𝐼𝐼 = −6 𝑁/𝑚𝑚²(facette horizontale)
facette à 30° : 𝜎 = 12 𝑀𝑃𝑎 & 𝜏 = 10,39 𝑀𝑃𝑎
facette à 60° : 𝜎 = 0 𝑀𝑃𝑎 & 𝜏 = 10,39 𝑀𝑃𝑎
𝜏 [𝑘𝑁/𝑐𝑚²]
𝜎 [𝑘𝑁/𝑐𝑚²]](https://image.slidesharecdn.com/exercicesmds1-220809160754-b40eaa67/85/Mecanique-des-structures-et-RDM-Exercices-corriges-99-320.jpg)
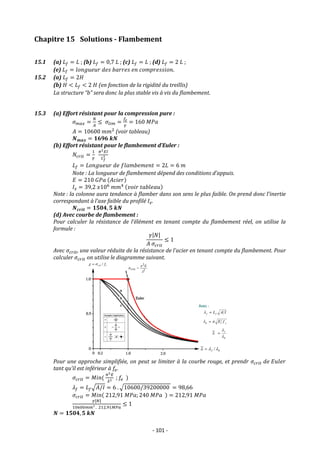
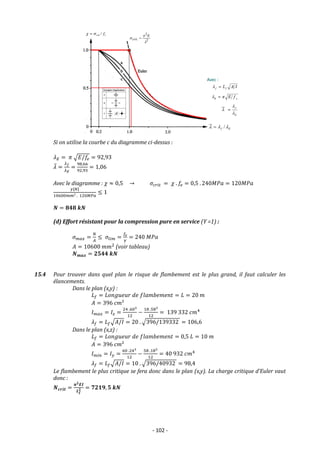
![- 106 -
15.8 (a) Flambement en dehors du plan de treillis :
I = 51,3 𝑥 106
[𝒎𝒎𝟒
] 𝑳𝒇 = 10 [m]
(b) Sans flambement :
𝐹𝑚𝑎𝑥 = 𝑓𝑒 𝐴 = 355 . 11 800 = 𝟒𝟏𝟖𝟗 𝒌𝑵
(c) Euler :
𝑁𝑐𝑟 =
𝜋²𝐸𝐼
𝐿𝑓
2 =
𝜋² .210 000 .51,3 𝑥106
10 0002 = 𝟏𝟎𝟔𝟑, 𝟐𝟓 𝒌𝑵
(d) Avec courbe de flambement :
Critère de résistance :
𝑁
𝐴 .𝜎𝑐𝑟𝑖𝑡
≤ 1
= 𝐿𝑓 √
𝐴
𝐼
= 10 000 √
11 800
51,3 𝑥106 = 𝟏𝟓𝟏, 𝟔𝟔
𝑬 = 𝝅 √
𝑬
𝒇𝒆
= 𝟕𝟔, 𝟒𝟏
̅ =
𝑬
= 𝟏, 𝟗𝟖
En utilisant la courbe « c » du diagramme :
= 0,2 → 𝜎𝑐𝑟𝑖𝑡 = . 𝑓𝑒 = 71 → 𝑁 = 𝐴 . 𝜎𝑐𝑟𝑖𝑡 = 𝟖𝟑𝟕, 𝟕𝟗 𝒌𝑵](https://image.slidesharecdn.com/exercicesmds1-220809160754-b40eaa67/85/Mecanique-des-structures-et-RDM-Exercices-corriges-106-320.jpg)
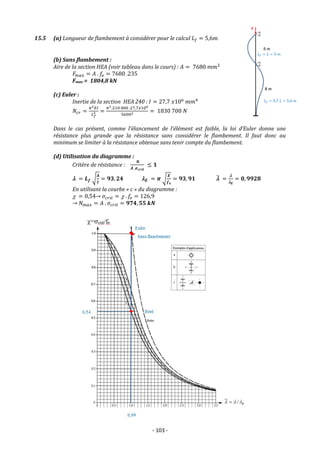
![- 107 -
15.9 (a) Longueur de flambement :
0,7 . 4 𝑚 = 2,8 𝑚 ≤ 3 𝑚
𝑳𝒇 = 𝟑 [𝒎]
(b) Calcul la résistance nécessaire 𝒇𝒆 :
Avec la courbe « c »
𝝌 = 𝟎, 𝟓 →
̅ ≈ 𝟏, 𝟎𝟔
̅ =
𝒇
𝑬
𝒇 = 𝑳𝒇√
𝑨
𝑰
= 𝟑 √
𝝅𝑹²
𝝅𝑹𝟒
𝟒
= 𝟑 √𝟒𝟎𝟎 = 𝟔𝟎
̅ =
𝒇
𝑬
=
𝟔𝟎
𝝅√
𝑬
𝒇𝒆
= 𝟏, 𝟎𝟔
𝒇𝒆 =
𝑬
(
𝟔𝟎
𝝅 .𝟏,𝟎𝟔
)
𝟐 =
𝟏𝟎 𝟎𝟎𝟎
𝟑𝟐𝟒,𝟔𝟑
= 𝟑𝟎, 𝟖 𝑴𝑷𝒂](https://image.slidesharecdn.com/exercicesmds1-220809160754-b40eaa67/85/Mecanique-des-structures-et-RDM-Exercices-corriges-107-320.jpg)
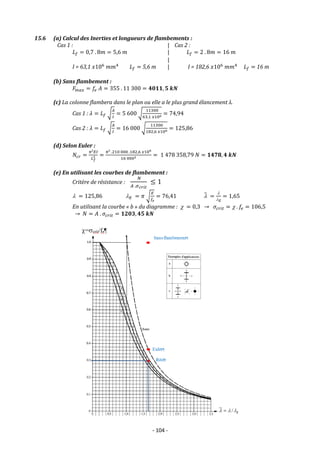
![- 108 -
15.10 (a) Forme et longueur de flambement :
𝑳𝒇 = 𝟒 [𝒎]
(b) Calcul de la charge maximale en tenant compte de la formule d’Euler :
Inertie de la section HEA 240 : 𝐼 = 27,7 𝑥106
𝑚𝑚4
𝐹𝑚𝑎𝑥 =
𝜋²𝐸𝐼
𝐿𝑓
2 =
𝜋² .210 000 .27,7𝑥106
4 0002 = 3 588 218 𝑁 = 3 588 [kN]
(c) Calcul de la charge maximale en utilisant les diagrammes de flambement :
Critère de résistance :
𝑵
𝑨 .𝝈𝒄𝒓𝒊𝒕
≤ 𝟏
= 𝑳𝒇 √
𝑨
𝑰
= 𝟔𝟔, 𝟔 𝑬 = 𝝅 √
𝑬
𝒇𝒆
= 𝟏𝟎𝟏, 𝟖
̅ =
𝑬
= 𝟎, 𝟔𝟓𝟒
En utilisant la courbe « c » du diagramme : = 0,74 → 𝜎𝑐𝑟𝑖𝑡 = . 𝑓𝑒 = 148
→ 𝐹𝑚𝑎𝑥 = 𝐴 . 𝜎𝑐𝑟𝑖𝑡 = 𝟏 𝟏𝟑𝟕 𝒌𝑵
L’élancement de la colonne étant très faible, la formule simplifiée d’Euler ne donne pas de
résultats cohérents car la résistance proposée est supérieure à la résistance du profilé sans
tenir compte du flambement](https://image.slidesharecdn.com/exercicesmds1-220809160754-b40eaa67/85/Mecanique-des-structures-et-RDM-Exercices-corriges-108-320.jpg)
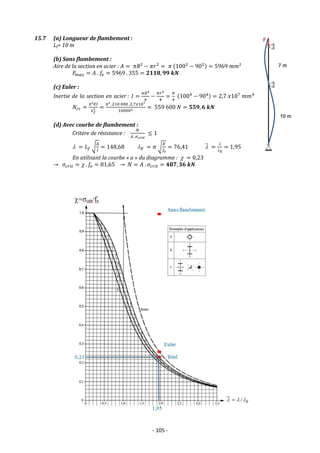
![- 109 -
15.11 (a) Longueur de flambement :
𝐿𝑓 = 4[𝑚]
(b) Dimensionnement avec la formule de Euler :
𝐹𝑚𝑎𝑥 = 500 𝑘𝑁 =
𝜋²𝐸𝐼
𝐿𝑓
2
𝐼 = 3,86 . 106
𝑚𝑚4
Section HEA : HEA 140 Section circulaire : D = 114,3 [mm]
(c) Dimensionnement avec les courbes de flambement :
Critère de résistance :
𝟏,𝟓 .𝑵
𝑨 .𝝈𝒄𝒓𝒊𝒕
≤ 𝟏
𝑬 = 𝝅 √
𝑬
𝒇𝒆
= 𝟏𝟎𝟏, 𝟖𝟎 |
Section HEA :
𝜆 = 𝐿𝑓 √
𝐴
𝐼
= 4 000 √
3140
3,89 𝑥106 = 113,64
̅ =
𝑬
= 𝟏, 𝟏𝟐
𝐴𝑣𝑒𝑐 𝑙𝑎 𝑐𝑜𝑢𝑟𝑏𝑒 𝑐
= 0,46 → 𝜎𝑐𝑟𝑖𝑡 = . 𝑓𝑒
→ 𝑁𝑚𝑎𝑥 = 𝐴 . 𝜎𝑐𝑟𝑖𝑡 = 𝟐𝟖𝟖, 𝟖𝟖 𝒌𝑵
Section circulaire :
𝜆 = 𝐿𝑓 √
𝐴
𝐼
= 107,99
̅ =
𝑬
= 𝟏, 𝟎𝟔
𝐴𝑣𝑒𝑐 𝑙𝑎 𝑐𝑜𝑢𝑟𝑏𝑒 𝑎
= 0,61 → 𝜎𝑐𝑟𝑖𝑡 = . 𝑓𝑒
→ 𝑁𝑚𝑎𝑥 = 𝐴 . 𝜎𝑐𝑟𝑖𝑡 = 𝟒𝟎𝟎, 𝟏𝟔 𝒌𝑵](https://image.slidesharecdn.com/exercicesmds1-220809160754-b40eaa67/85/Mecanique-des-structures-et-RDM-Exercices-corriges-109-320.jpg)
![- 110 -
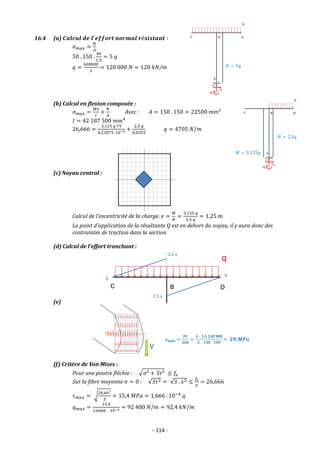
Chapitre 16 Solutions - Exercices récapitulatifs
16.1 (a) Charge et moment dû au poids propre :
(b) Effort dans le câble :
q = PP du béton = 9,6 kN
Pour une parabole :
𝑅𝐻 =
𝑞𝐿2
8𝐻
=
9,6 . 102
8 . 0,3
= 400 𝑘𝑁
𝑅𝑉 =
𝑞𝐿
2
=
9,6 . 10
2
= 48 𝑘𝑁
𝑃 = √𝑅𝐻² + 𝑅𝑉² = 402,87 𝑘𝑁
(c) Moments dus à P :
(d) Efforts normaux dus à P :
(e)& (f) Effort dans la structure (PP+câble) :
(g) Contraintes normales dans la section :
max = 1,6 [MPa] Compression min= 0,4 [MPa] Compression](https://image.slidesharecdn.com/exercicesmds1-220809160754-b40eaa67/85/Mecanique-des-structures-et-RDM-Exercices-corriges-110-320.jpg)
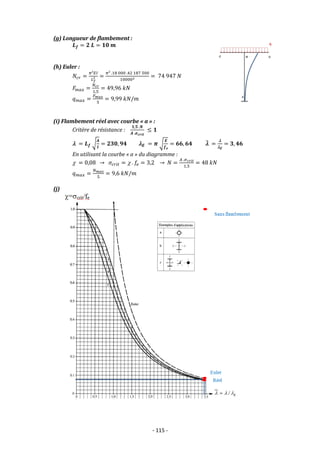
![- 112 -
16.3 (a) Calcul de la charge répartie :
On part de la formule
𝑷 = 𝟐𝟐𝟎 𝑵 = √(
𝒒𝑳
𝟐
)
𝟐
+ (
𝒒𝑳𝟐
𝟖𝒇
)
𝟐
→ 𝑞 = √
𝑃2
(
𝐿2
4
+
𝐿4
64𝑓2)
= 0,976 𝑁/𝑚
(b) Calcul de P pour limiter la flèche du câble :
𝑷 = √(
𝒒𝑳
𝟐
)
𝟐
+ (
𝒒𝑳𝟐
𝟖𝒇
)
𝟐
= 𝟒𝟑𝟗, 𝟒𝟒 𝑵
On peut arrondir à P = 440 N
(c)
La tension max ne change pas et vaut la valeur du contrepoids : 440 N
𝑷 = 𝟒𝟒𝟎 𝑵 = √(
𝒒𝑳
𝟐
)
𝟐
+ (
𝒒𝑳𝟐
𝟖𝒇
)
𝟐
→ 𝑓 =
𝑞𝐿2
8 √𝑃2−(
𝑞𝐿
2
)
2
= 0,442 𝑚
(d) Noyau central :
𝝈𝒆𝒙𝒕 =
𝑴𝒗
𝑰
−
𝑵
𝑨
= 𝟎 =
𝑭 . 𝒓 . 𝑹
𝝅𝑹𝟒
𝟒
−
𝑭
𝝅𝑹𝟐
𝐹𝑉1 =
𝑞𝐿
2
= 14,64 𝑘𝑁 & 𝐹𝐻1 = √𝑃² − 𝐹𝑉
2
= 439,7564 𝑁
𝐹𝑉2 =
𝑞𝐿
2
= 25,89 𝑘𝑁 & 𝐹𝐻2 = √𝑃² − 𝐹𝑉
2
= 439,237 𝑁
𝐹𝑉𝑡𝑜𝑡 = 40,53 𝑘𝑁 & 𝐹𝐻𝑡𝑜𝑡 = 0,5187 𝑁
Ce qui nous donne en pieds de poteau 𝑀𝑚𝑎𝑥 = 0,5187 . 8 = 4,15 𝑁𝑚 & 𝑁 = 40,53 𝑁
On peut calculer =
𝑀
𝑁
= 0,1 𝑚 , et on voit que la résultante des efforts est en dehors du noyau
central, il y aura donc des contraintes de traction.
(e) Calcul de la contrainte normale maximale dans le poteau central :
𝝈𝒎𝒂𝒙 =
𝑴𝒗
𝑰
+
𝑵
𝑨
≤
𝒇𝒆
𝜸
𝜎𝑚𝑎𝑥 =
4,15 𝑅
𝜋𝑅4
4
+
40,53
𝜋𝑅²
≤
𝑓𝑒
𝛾
= 10 𝑀𝑝𝑎
𝜎𝑚𝑎𝑥 =
4 .4,15
𝜋 753 +
40,53
𝜋 75²
≤
𝑓𝑒
𝛾
= 10 𝑀𝑝𝑎
𝜎𝑚𝑎𝑥 = 0,0148 𝑀𝑝𝑎 ≤ 10 𝑀𝑝𝑎 Le poteau résiste bien.
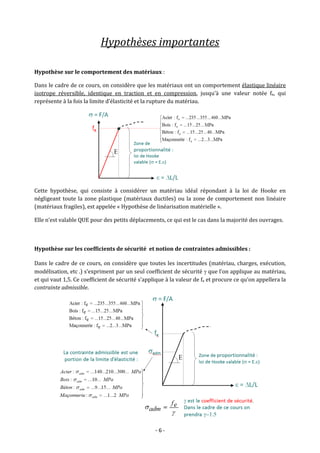
(f) Forme de flambement du poteau central et inertie :
𝐼 =
𝜋𝑅4
4
= 2,48 . 107
[𝒎𝒎𝟒
]
𝑳𝒇 = 16 [m]
r = R/4](https://image.slidesharecdn.com/exercicesmds1-220809160754-b40eaa67/85/Mecanique-des-structures-et-RDM-Exercices-corriges-112-320.jpg)
![- 113 -
(g) Calcul de la charge maximale en négligeant la sensibilité au flambement :
Aire de la section : 𝐴 = 𝜋𝑅² = 𝜋 75² = 17 671 𝑚𝑚²
𝐹𝑚𝑎𝑥 = 𝐴 .
𝑓𝑒
𝛾
= 17 671 .
15
1,5
= 176,71[kN]
(h) Calcul de la charge maximale en tenant compte de la formule d’Euler :
𝑁𝑐𝑟 =
𝜋²𝐸𝐼
𝐿𝑓
2 =
𝜋² .10 000 .17 671
160002 = 9 560 𝑁
𝐹𝑚𝑎𝑥 =
𝑁𝑐𝑟
1,5
Fmax = 6,37 [kN]
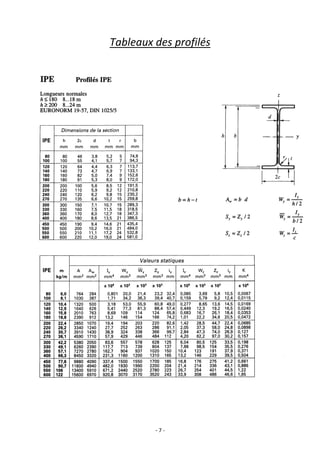
(i) Calcul de la charge maximale pouvant être appliqué sur le poteau central :
On utilise la courbe « c ».
𝑓 = 426,67
𝐸 = 81,11
̅ = 5,26
Comme notre élément est fortement élancé, on voit que la formule d’Euler donne une très
bonne approximation de la résistance du poteau (la courbe « c » est presque confondue avec la
courbe d’Euler). → 𝐹𝑚𝑎𝑥 = 6,37 𝑘𝑁](https://image.slidesharecdn.com/exercicesmds1-220809160754-b40eaa67/85/Mecanique-des-structures-et-RDM-Exercices-corriges-113-320.jpg)